4H-SiC nMOSFETs的亚阈值漏电流扫描滞后特性
目录
- 标题:On the Subthreshold Drain Current Sweep Hysteresis of 4H-SiC nMOSFETs
- 研究了什么
- 文章创新点
- 文章的研究方法
- 文章得出的结论
标题:On the Subthreshold Drain Current Sweep Hysteresis of 4H-SiC nMOSFETs

亚阈值滞后(Subthreshold hysteresis)是指在MOSFET等器件中,在从积累到反转和反之间进行栅极电压扫描时,漏电流与栅极电压之间的滞后现象。具体来说,当栅极电压从积累区向反转区移动时,漏电流并不是平滑地变化,而是存在一定的滞后,即漏电流的变化速度没有栅极电压的变化速度快。这种滞后现象可能会导致器件性能的不稳定,影响器件的可靠性和性能。
Si-face (0001)和a-face (1120)是指4H-SiC(4H-硅碳化物)晶体的两个不同的晶面。其中,Si-face (0001)晶面是指晶体表面平行于晶体中心的[0001]晶向的表面,而a-face (1120)晶面则是指晶体表面平行于[1120]晶向的表面。在SiC器件中,不同的晶面具有不同的电学特性和器件性能,因此需要对它们进行研究和比较,以优化器件设计和制备工艺。
研究了什么
摘要—我们研究了4H 碳化硅 (SiC) 的亚阈值漏极电流滞后 Si 面 (0001) 和 a 面 (1120) n 通道功率 MOSFET 在从积累到反转和反向的栅极电压扫描之间。取决于栅极电压扫描的方向,MOSFET 在相同的栅极电压下显示不同的亚阈值漏极电流。观察到的上扫描和下扫描之间的滞后可以表示为亚阈值电压的变化,可能达到几伏。我们表明,电压变化是由于在积累过程中在边界陷阱中捕获空穴引起的,并且与电荷泵信号直接成比例。电压变化可以通过在阈值电压以上施加栅极偏置来完全恢复,并且不会影响器件可靠性。
术语索引—4H-SiC、MOSFET、亚阈值滞后、边界态、Si 面、a 面
该文章研究了4H-SiC Si面(0001)和a面(1120)n型功率MOSFET的次阈值漏电流扫描滞后现象,包括从积累到反转和反之亦然的栅压扫描。研究表明,根据栅电压扫描的方向,MOSFET在相同的栅电压下显示不同的次阈值漏电流。观察到的上扫和下扫之间的滞后可以表示为次阈值电压漂移,可能达到几伏特。电压漂移是由于在积累过程中边界陷阱中的空穴俘获引起的,并且与电荷泵浦信号成正比。通过施加高于阈值电压的栅偏压,电压漂移是完全可恢复的,不会影响器件可靠性。
文章创新点
该文章的创新点包括:
- 研究了4H-SiC Si面(0001)和a面(1120)n型功率MOSFET的次阈值漏电流扫描滞后现象。
- 观察到在相同的栅电压下,根据栅电压扫描的方向,MOSFET显示不同的次阈值漏电流。
- 将观察到的上扫和下扫之间的滞后表达为次阈值电压漂移,可能达到几伏特。
- 确认了在积累过程中边界陷阱中的空穴俘获是电压漂移的原因。
- 电压漂移与电荷泵浦信号成正比。
- 通过施加高于阈值电压的栅偏压,电压漂移是完全可恢复的。
- 电压漂移对器件可靠性没有影响。
文章的研究方法
该文章的研究方法涉及对4H-SiC Si面(0001)和a面(1120)MOSFET进行栅电压上升和下降扫描时的次阈值漏电流滞后现象的研究。该研究使用光谱电荷泵浦技术来研究扫描滞后,因为它对界面和边界态敏感。还分析了恒定高电平和恒定基准电平电荷泵浦测量中每个周期泵送电荷数NCP的温度依赖性。使用光谱电荷泵浦提取了界面/边界态密度Dit的能量分布。该研究还比较了Si面和a面器件获得的结果。
文章得出的结论
该文章得出的结论包括:
- 4H-SiC Si面(0001)和a面(1120)MOSFET的次阈值漏电流滞后现象与基于硅的功率器件有明显不同。
- 观察到的上扫和下扫之间的滞后可以表示为次阈值电压漂移,其与电荷泵浦信号成比例,并且在高于阈值电压的栅电压下消失。
- a面和Si面器件的次阈值电压漂移和迁移率的差异可以通过通过光谱电荷泵浦获得的边界态能量分布来解释。
- 由于在中间能隙附近存在更高的边界态密度,a面器件表现出更明显的滞后现象,但由于在4H-SiC导带边缘附近存在更低的边界态密度,a面器件也表现出更高的迁移率。
- 通过将器件偏置在或接近其阈值电压附近,可以完全恢复次阈值电压漂移。
- 尽管在次阈值区域存在滞后效应,但SiC-MOSFET的正常关断特性在任何开关情况下都得以保持。
相关文章:

4H-SiC nMOSFETs的亚阈值漏电流扫描滞后特性
目录 标题:On the Subthreshold Drain Current Sweep Hysteresis of 4H-SiC nMOSFETs研究了什么文章创新点文章的研究方法文章得出的结论 标题:On the Subthreshold Drain Current Sweep Hysteresis of 4H-SiC nMOSFETs 亚阈值滞后(Subthresh…...
)
设计模式(单例模式)
概念 保证指定的类只有一个实例,不能创建出其他的实例 实现方式 1.饿汉模式 1.1 代码展示 package 设计模式;/*** Created with IntelliJ IDEA.* Description:* User: wuyulin* Date: 2023-07-28* Time: 11:28*///单例模式(饿汉模式) //保证…...

[SQL挖掘机] - 算术函数 - sqrt
介绍: 当谈到 SQL 中的 sqrt 函数时,它用于计算一个数值的平方根。 用法: sqrt 函数使用以下语法: sqrt(x)其中,x 是要计算平方根的数值。 注意: 当使用负数参数调用 SQL 中的 sqrt 函数时,具体的错误消息可能因不同的数据库…...

数据结构--顺序表、单链表
线性表是指顺序表和单链表 //顺序表数据结构 typedef struct { ElemType data[MaxSize];//顺序表元素 int length; //顺序表当前长度 }SqList; //单链表结点数据结构 typedef struct LNode { ElemType data;//数据域 struct LNode *next;//指针域 }LNode,*LinkList; 顺序表 …...
之 云原生)
云安全攻防(一)之 云原生
前言 随着公有云和私有云的广泛部署,云计算基础设施成为企业部署新业务的首选。可以说,云计算已进入下半场,各大云计算服务商的厮杀日益激烈,新的概念也不断的层出不穷。近年来,云原生安全(Cloud Native C…...
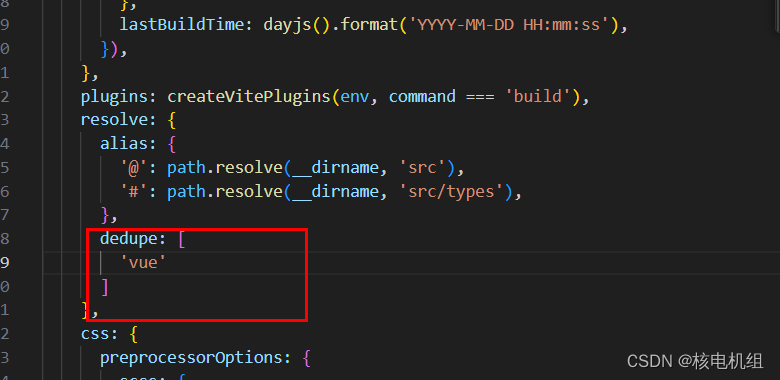
#vue3报错 Cannot read properties of null (reading ‘isCE‘)#
场景:使用 npm 安装依赖包的时候,如如安装 npm i xlsx npm i file-saver 重新运行报错 Cannot read properties of null (reading isCE)# 解决办法: 使用的vite vue 在vite.config.ts添加如下配置: dedupe: [ vue ]...

【计算机视觉中的 GAN 】 - 生成学习简介(1)
一、说明 在阅读本文之前,强烈建议先阅读预备知识,否则缺乏必要的推理基础。本文是相同理论GAN原理的具体化范例,阅读后有两个好处:1 巩固了已经建立的GAN基本概念 2 对具体应用的过程和套路进行常识学习,这种练习题一…...

深度学习实战44-Keras框架下实现高中数学题目的智能分类功能应用
大家好,我是微学AI ,今天给大家介绍一下深度学习实战44-Keras框架实现高中数学题目的智能分类功能应用,该功能是基于人工智能技术的创新应用,通过对数学题目进行智能分类,提供个性化的学习辅助和教学支持。该功能的实现可以通过以下步骤:首先,采集大量的高中数学题目数据…...

Redis Sentinel 及 Redis Cluster
Redis Sentinel Redis-Sentinel(哨兵模式)是Redis官方推荐的高可用性(HA)解决方案,当用Redis做Master-slave的高可用方案时,假如master宕机了,Redis本身(包括它的很多客户端)都没有实现自动进行主备切换,而Redis-sentinel本身也是…...

shell中按照特定字符分割字符串,并且在切分后的每段内容后加上特定字符(串),然后再用特定字符拼接起来
文件中的内容,可以这么写: awk -F, -v OFS, {for(i1;i<NF;i){$i$i"_suffix"}}1 input.txt-F,:设置输入字段分隔符为逗号(,),这将使awk按照逗号分割输入文本。-v OFS‘,’:设置输…...

探寻智能化未来:AI与Web3共创金融领域巨大潜力
人工智能(AI)和Web3技术的迅猛发展为我们带来了许多新的机遇和影响。在数字经济和社会的浪潮中,结合了AI的智能化能力和Web3的去中心化与区块链技术,我们将进入一个智能化的Web3时代。人工智能和Web3技术是开拓生产力极限和重新定…...
Django学习笔记-表单(forms)的使用
在Django中提供了了form表单,可以更为简单的创建表单模板信息,简化html的表单。 一、网页应用程序中表单的应用 表单通常用来作为提交数据时候使用。 1.1 创建表单模板文件夹 在项目文件夹下创建一个template文件夹,用于存储所有的html模…...

机器学习分布式框架ray运行TensorFlow实例
使用Ray来实现TensorFlow的训练是一种并行化和分布式的方法,它可以有效地加速大规模数据集上的深度学习模型的训练过程。Ray是一个高性能、分布式计算框架,可以在集群上进行任务并行化和数据并行化,从而提高训练速度和可扩展性。 以下是实现…...
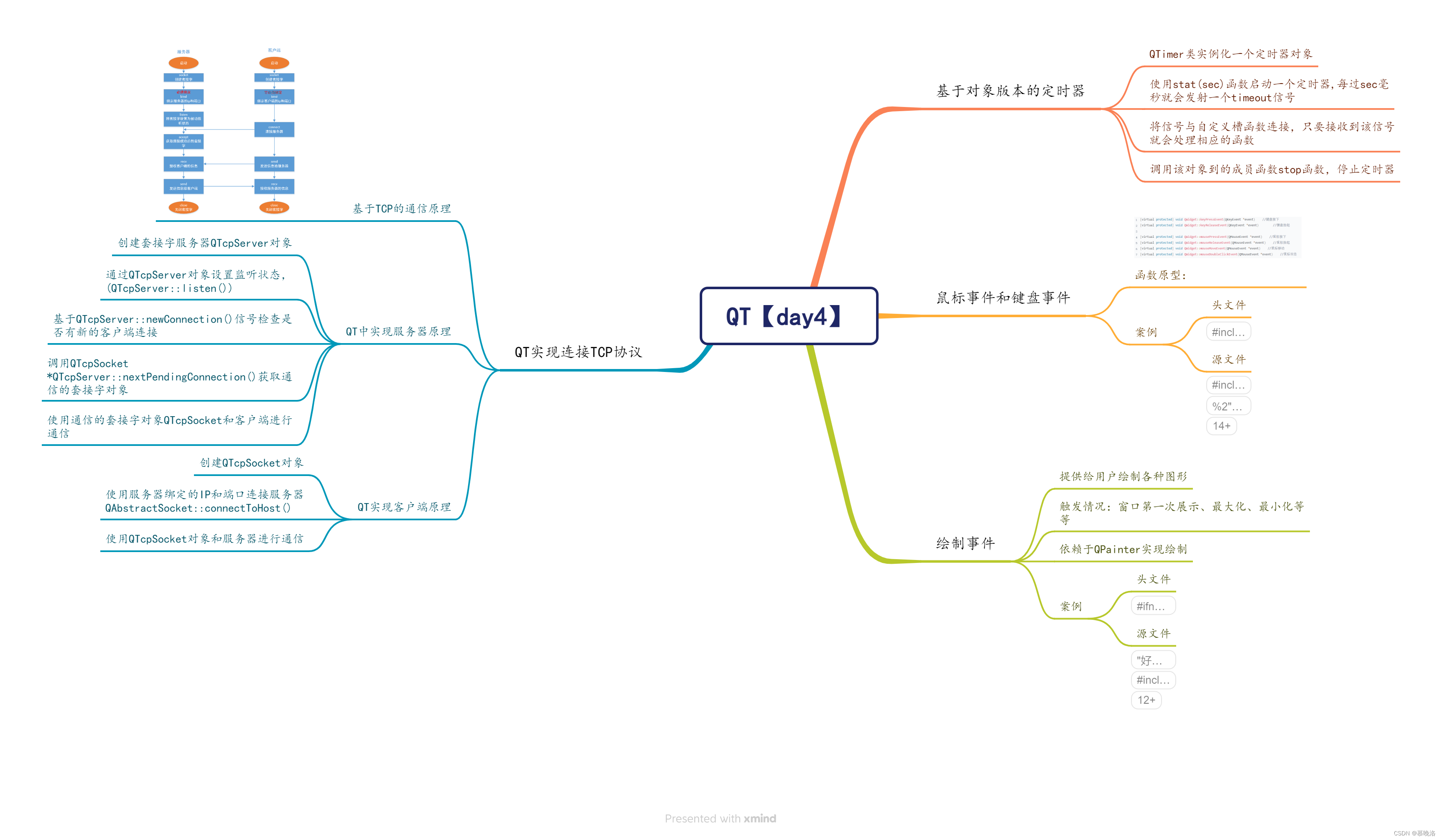
QT【day4】
chat_QT服务器端: //.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include<QTcpServer> //服务器类 #include<QTcpSocket> //客户端类 #include<QMessageBox> //对话框类 #include<QList> //链表容器 #inc…...

java中方法相关知识点详解
方法 简介 方法是一段用来完成特定功能的代码片段,用于定义该类或该类的实例的行为特征和功能实现语句块【复合语句】 语句块中定义的变量只能用于自己,外部不能使用 语句块可以使用外部的变量,而外部不能使用语句块的变量语法 [修饰符1 修饰…...

【算法训练营】Fibonacci数列+合法括号序列判断+两种排序方法
7.29 Fibonacci数列题目解析代码 合法括号序列判断题目题解代码 两种排序方法题目:题解代码 Fibonacci数列 题目 题目链接: 点击跳转 解析 【题目解析】: 本题是对于Fibonacci数列的一个考察,Fibonacci数列的性质是第一项和第二项都为1&am…...
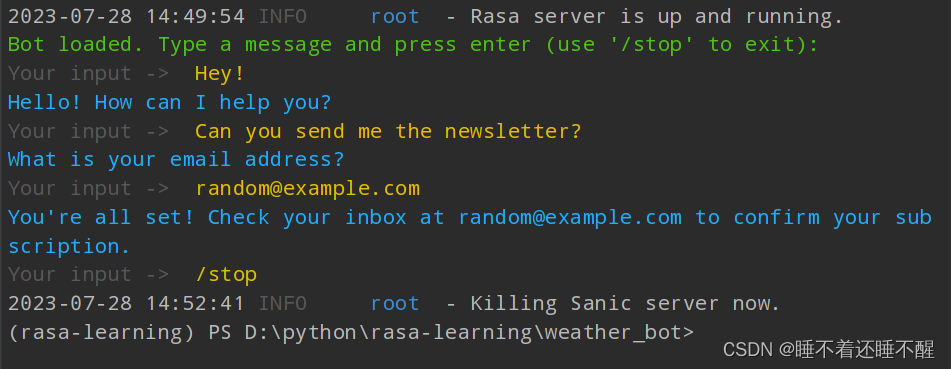
【Rasa】入门案例学习
Rasa初体验--构建对话机器人 NLU数据 version: "3.1"nlu:- intent: greetexamples: |- Hi- Hey!- Hello- Good day- Good morning- intent: subscribeexamples: |- I want to get the newsletter- Can you send me the newsletter?- Can you sign me up for the ne…...

基于java的坦克大战游戏的设计与实现--开题报告--【毕业论文】
文章目录 本系列校训毕设的技术铺垫文章主体层次选题目的和意义:与本课题相关的技术和方法综述:主要设计内容:设计的环境、方法及措施:参考文献 配套资源 本系列校训 互相伤害互相卷,玩命学习要你管,天生我…...

学习笔记|百度文心千帆大模型平台测试及页面交互简易代码
目前百度文心一言的内测资格申请相当拉胯,提交申请快3个月,无任何音讯。不知道要等到什么时候。 百度适时开放了百度文心千帆大模型平台,目前可以提交申请测试,貌似通过的很快,已取得测试申请资格,可以用起…...

Python中的数据科学实验库有哪些?
Python中有许多数据科学实验库可供使用。以下是一些常用的库: NumPy:用于处理大型多维数组和矩阵的基础数学库。Pandas:用于数据处理和分析的库,提供了灵活的数据结构和数据操作工具。Matplotlib:用于创建静态、动态和…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
