堆结构——面试算法题高频汇总
目录
引言
堆创建&增删改
堆构造过程
举个例子
堆插入元素
删除元素
在数组中找第k大的元素
举例
堆排序原理
合并k个排序链表
数据流中位数问题
引言
堆是将一组数据按照完全二叉树的存储顺序,将数据存储在一个一维数组中的结构。堆有两种结构,一种称为大顶堆,一种称为小顶堆。
-
小顶堆:任意节点的值均小于等于它的左右孩子,并且最小的值位于堆顶,即根节点处。
-
大顶堆:任意节点的值均大于等于它的左右孩子,并且最大的值位于堆顶,即根节点处。 有些地方也叫大根堆、小根堆,或者最大堆、最小堆都一个意思。
在Java领域,可以认为堆 就是优先级队列,反之亦然。
规律:查找:找大用小,大的进;找小用大,小的进。
排序:升序用小,降序用大。
堆创建&增删改
堆构造过程
使用数组构建堆时,就是先按照层次将所有元素依次填入二叉树中,使其成为二叉树,然后再不断调整,最终使其符合堆结构。
举个例子
比如数组是[3,1,4,5,2],先按层排成小树:
3是树顶,下面左孩子1,右孩子4,第三层左孩子5和右孩子2。这时候树乱糟糟的,不符合堆(比如大顶堆)要求~于是从倒数第二层开始调整,先看数字1,它的左孩子5比它大,交换它们变成[3,5,4,1,2];再往上调整树顶3,它的左孩子5比它大,交换后变成[5,3,4,1,2],但交换后3的位置又需要和它的左孩子1比,发现没问题,调整完毕!现在整棵树像叠罗汉一样,每个爸爸都比孩子大,堆就建好啦
堆插入元素
从上面可以看到根节点和其左右子节点是堆里的老大老二和老三,其他结点则没有太明显的规律,那如果要插入一个新元素,该怎么做呢?直接说规则,将元素插入到保持其为完全二叉树的最后一个位置,然后顺着这条支路一直向上调整,每前进一层就要保证其子树都满足堆否则就去处理子树,直到完全满足要求。
删除元素
堆本身比较特殊,一般对堆中的数据进行操作都是针对堆顶的元素,即每次都从堆中获得最大值或最小值,其他的不关心,所以我们删除的时候,也是删除堆顶。
在数组中找第k大的元素
给定整数数组nums和整数k,请返回数组中第k个最大的元素。 请注意,你需要找的是数组排序后的第k个最大的元素,而不是第k个不同的元素。
-
选择【暴力循环】
-
快排方法【之前博客有,点击查看】
-
堆查找法
关于堆查找法的思路:
找最大用小堆,找最小用大堆,找中间用两个堆
举例
序列[3,2,3,1, 2 ,4 ,5, 1,5,6,2,3],k为4。
我们构造一个大小只有4的小根堆,堆满了之后,对于小根堆,并一定所有新来的元素都可以入堆的,只有大于根元素的才可以插入到堆中,否则就直接抛弃。这是一个很重要的前提。
元素进入的时候,先替换根元素,如果发现左右两个子树都小该怎么办呢?很显然应该与更小的那个比较,这样才能保证根元素一定是当前堆最小的。
新元素插入的时候只是替换根元素,然后重新构造成小堆,完成之后,你会神奇的发现此时根的根元素正好是第4大的元素。
这时候你会发现,不管要处理的序列有多大,或者是不是固定的,根元素每次都恰好是当前序列下的第K大元素。
由于找第 K 大元素,其实就是整个数组排序以后后半部分最小的那个元素。因此,我们可以维护一个有 K 个元素的最小堆:
-
如果当前堆不满,直接添加;
-
堆满的时候,如果新读到的数小于等于堆顶,肯定不是我们要找的元素,只有新遍历到的数大于堆顶的时候,才将堆顶拿出,然后放入新读到的数,进而让堆自己去调整内部结构。
import java.util.PriorityQueue;
public class Solution {public int findKthLargest(int[] nums, int k) {if(k>nums.length){return -1;}int len = nums.length;// 使用一个含有 k 个元素的最小堆PriorityQueue<Integer> minHeap = new PriorityQueue<>(k, (a, b) -> a - b);for (int i = 0; i < k; i++) {minHeap.add(nums[i]);}for (int i = k; i < len; i++) {// 看一眼,不拿出,因为有可能没有必要替换Integer topEle = minHeap.peek();// 只要当前遍历的元素比堆顶元素大,堆顶弹出,遍历的元素进去if (nums[i] > topEle) {minHeap.poll();minHeap.offer(nums[i]);}}return minHeap.peek();}
}堆排序原理
根节点是整个结构最大的元素,先将其拿走,剩下的重排,此时根节点就是第二大的元素,再将其拿走,再排,依次类推。
合并k个排序链表
给你一个链表数组,每个链表都已经按升序排列。请你将所有链表合并到一个升序链表中,返回合并后的链表。
示例1:
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
给了数组,就建立多大的固定堆
给了几个数组,就建立多大的堆,固定大小的
public ListNode mergeKLists(ListNode[] lists) {if (lists == null || lists.length == 0) return null;PriorityQueue<ListNode> q = new PriorityQueue<>(Comparator.comparing(node -> node.val));for (int i = 0; i < lists.length; i++) {if (lists[i] != null) {q.add(lists[i]);}}ListNode dummy = new ListNode(0);ListNode tail = dummy;while (!q.isEmpty()) {tail.next = q.poll();tail = tail.next;if (tail.next != null) {q.add(tail.next);}}return dummy.next;
}数据流中位数问题
中位数是有序列表中间的数。如果列表长度是偶数,中位数则是中间两个数的平均值。
例如:[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5
设计一个支持以下两种操作的数据结构:
-
void addNum(int num) - 从数据流中添加一个整数到数据结构中。
-
double findMedian() - 返回目前所有元素的中位数。
进阶问题:
-
如果数据流中所有整数都在 0 到 100 范围内,你将如何优化你的算法?
-
如果数据流中 99% 的整数都在 0 到 100 范围内,你将如何优化你的算法?
思路
中位数的题,一般都可以用 大顶堆 + 小顶堆来求解
小顶堆(minHeap):存储所有元素中较大的一半,堆顶存储的是其中最小的数。
大顶堆(maxHeap):存储所有元素中较小的一半,堆顶存储的是其中最大的数。相当于,把所有元素分成了大和小两半,而我们计算中位数,只需要大的那半的最小值和小的那半的最大值即可。
class MedianFinder {// 小顶堆存储的是比较大的元素,堆顶是其中的最小值PriorityQueue<Integer> minHeap;// 大顶堆存储的是比较小的元素,堆顶是其中的最大值PriorityQueue<Integer> maxHeap;/** initialize your data structure here. */public MedianFinder() {this.minHeap = new PriorityQueue<>();this.maxHeap = new PriorityQueue<>((a, b) -> b - a);}public void addNum(int num) {// 小顶堆存储的是比较大的元素,num比较大元素中最小的还大,所以,进入minHeapif (minHeap.isEmpty() || num > minHeap.peek()) {minHeap.offer(num);// 如果minHeap比maxHeap多2个元素,就平衡一下if (minHeap.size() - maxHeap.size() > 1) {maxHeap.offer(minHeap.poll());}} else {maxHeap.offer(num);// 这样可以保证多的那个元素肯定在minHeapif (maxHeap.size() - minHeap.size() > 0) {minHeap.offer(maxHeap.poll());}}}public double findMedian() {if( minHeap.size() > maxHeap.size() ){return minHeap.peek();}else if(minHeap.size() < maxHeap.size() ) {return maxHeap.peek();}else{return ((minHeap.peek()+maxHeap.peek())/2.0;} }
}相关文章:

堆结构——面试算法题高频汇总
目录 引言 堆创建&增删改 堆构造过程 举个例子 堆插入元素 删除元素 在数组中找第k大的元素 举例 堆排序原理 合并k个排序链表 数据流中位数问题 引言 堆是将一组数据按照完全二叉树的存储顺序,将数据存储在一个一维数组中的结构。堆有两种结构&…...

httpx模块的使用
在使用requests模块发起请求时,报以下错误,表示服务器有可能使用的是http2.0协议版本,导致requests无法爬取。 此时就可以使用httpx模块爬取。 先下载httpx模块: pip install httpx[http2]然后用httpx发起请求: impo…...

Linux的: /proc/sys/net/ipv6/conf/ 笔记250405
Linux的: /proc/sys/net/ipv6/conf/ /proc/sys/net/ipv6/conf/ 是 Linux 系统中用于 动态配置 IPv6 网络接口参数 的核心目录。它允许针对不同网络接口(如 eth0、wlan0)或全局设置(all)调整 IPv6 协议栈的行为。 它通过虚拟文件系…...
论文阅读10——解开碳排放与碳足迹之间的关系:文献回顾和可持续交通框架
原文地址: Unraveling the relation between carbon emission and carbon footprint: A literature review and framework for sustainable transportation | npj Sustainable Mobility and TransportTransportation decarbonization has drawn enormous attention globally,…...

新一代AI架构实践:数字大脑AI+智能调度MCP+领域执行APP的黄金金字塔体系
新一代AI架构实践:数字大脑智能调度领域执行的黄金金字塔体系 一、架构本质的三层穿透性认知 1.1 核心范式转变(CPS理论升级) 传统算法架构:数据驱动 → 特征工程 → 模型训练 → 业务应用 新一代AI架构:物理规律建…...

Winform MQTT客户端连接方式
项目中使用到Winform的数据转发服务,所以记录下使用到的方法。 一.创建单例模板 using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks;namespace ConsoleApp.Scripts {public class SingleTon&…...

Linux Bash 脚本实战:自动监控域名证书过期并发送邮件告警
在日常运维工作中,SSL 证书的管理是一个非常重要的环节,尤其对于线上业务来说,证书到期会直接导致服务不可用。为了避免证书到期带来的风险,我们可以编写一个 Bash 脚本来自动检测域名的 SSL 证书过期时间,并在证书即将到期时发送告警邮件。 目录 脚本功能概述 代码实现…...

什么是异步?
什么是异步? 异步是一个术语,用于描述不需要同时行动或协调就能独立运行的流程。这一概念在技术和计算领域尤为重要,它允许系统的不同部分按自己的节奏运行,而无需等待同步信号或事件。在区块链技术中,异步是指网络中…...
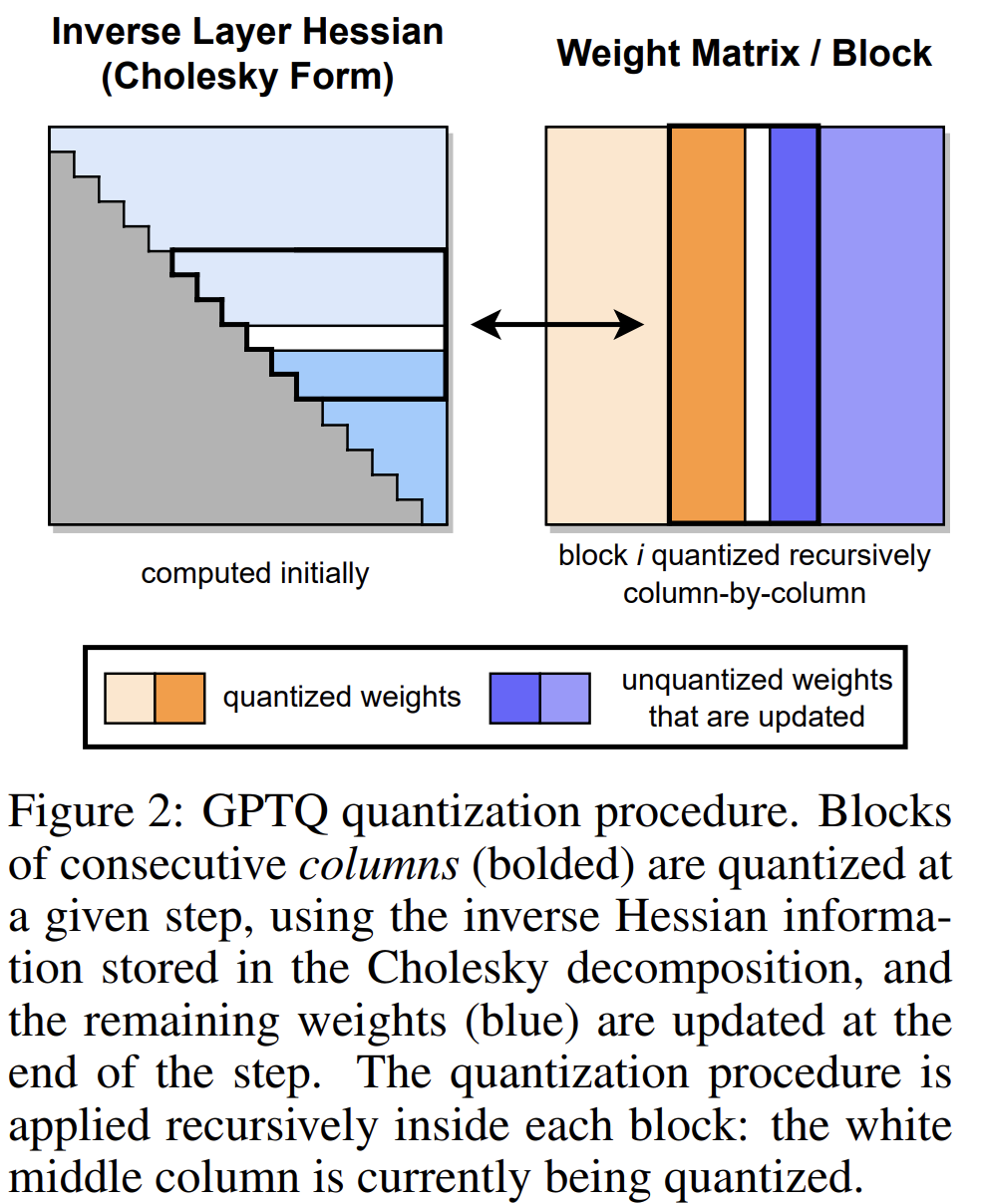
【模型量化】GPTQ 与 AutoGPTQ
GPTQ是一种用于类GPT线性最小二乘法的量化方法,它使用基于近似二阶信息的一次加权量化。 本文中也展示了如何使用量化模型以及如何量化自己的模型AutoGPTQ。 AutoGPTQ:一个易于使用的LLM量化包,带有用户友好的API,基于GPTQ算法(仅…...

学透Spring Boot — 018. 优雅支持多种响应格式
这是我的专栏《学透Spring Boot》的第18篇文章,想要更系统的学习Spring Boot,请访问我的专栏:学透 Spring Boot_postnull咖啡的博客-CSDN博客。 目录 返回不同格式的响应 Spring Boot的内容协商 控制器不用任何修改 启动内容协商配置 访…...
Ma)
Java小白-管理项目工具Maven(3)Ma
一、pom.xml文件 pom.xml 文件是 Maven(Apache Maven)项目的核心配置文件,它定义了项目的构建、依赖管理和项目元数据等信息。Maven 是一个流行的 Java 项目管理和构建自动化工具,而 pom.xml 是 Maven 项目中不可或缺的一部分。 …...

C++中的多态和模板
#include <iostream> #include <cstdlib> #include <ctime> #include <string>using namespace std;// 武器基类 class Weapon { public:virtual ~Weapon() {}virtual string getName() const 0; // 获取武器名称virtual int getAtk() const 0; …...
)
Java 类型转换和泛型原理(JVM 层面)
一、类型转换 概念解释: 编译类型:在编译时确定,保存在虚拟机栈的栈帧中的局部变量表中; 运行类型:在运行时确定,由保存在局部变量表中变量指向的堆中对象实例的类型决定(存储在对象头中&…...

Wireshark 安装保姆教程(图文详解)
一、Wireshark 简介 Wireshark是使用最广泛的一款开源抓包软件,常用来检测网络问题、攻击溯源、或者分析底层通信机制。它使用WinPCAP作为接口,直接与网卡进行数据报文交换,它支持在 Windows、Mac OS、Linux 等多种主流操作系统上运行 &…...

下载安装Node.js及其他环境
提示:从Node版本降级到Vue项目运行 文章目录 下载Node.js环境配置配置环境变量 安装 cnpm(我需要安装)安装脚手架安装依赖安装淘宝镜像(注意会更新)cnpm vs npm 与新旧版本核心差异包管理器不同功能差异如何选择&#…...

机器视觉3D中激光偏镜的优点
机器视觉的3D应用中,激光偏镜(如偏振片、波片、偏振分束器等)通过其独特的偏振控制能力,显著提升了系统的测量精度、抗干扰能力和适应性。以下是其核心优点: 1. 提升3D成像精度 抑制环境光干扰:偏振片可滤除非偏振的环境杂光(如日光、室内照明),仅保留激光偏振信号,大…...

MyBatis Plus 在 ZKmall开源商城持久层的优化实践
ZKmall开源商城作为基于 Spring Cloud 的高性能电商平台,其持久层通过 MyBatis Plus 实现了多项深度优化,涵盖分库分表、缓存策略、分页性能、多租户隔离等核心场景。以下是具体实践总结: 一、分库分表与插件集成优化 1. 分库分表策略 Sh…...

rust 同时处理多个异步任务,并在一个任务完成退出
use std::thread; use tokio::{sync::mpsc,time::{sleep, Duration}, };async fn check_for_one() {// 该函数会每秒打印一次 "write"loop {println!("write");sleep(Duration::from_secs(1)).await;} }async fn start_print_task() -> Result<(), (…...

使用注解开发springMVC
引言 在学习过第一个springMVC项目建造过后,让我们直接进入真实开发中所必需的注解开发, 是何等的简洁高效!! 注:由于Maven可能存在资源过滤的问题,在maven依赖中加入 <build><resources>&l…...

深入解析 Java 8 Function 接口:函数式编程的核心工具
精心整理了最新的面试资料和简历模板,有需要的可以自行获取 点击前往百度网盘获取 点击前往夸克网盘获取 Java 8 引入的 java.util.function.Function 接口是函数式编程范式的核心组件之一,本文将全面解析其使用方法,并通过丰富的代码示例演…...

【Axure元件分享】时间范围选择器
时间范围选择器下拉选择开始时间和结束时间,实现效果如下。 源文件截图: 元件获取方式:...

【Linux操作系统——学习笔记三】Linux环境下多级目录构建与管理的命令行实践报告
1.在用户主目录下,使用以下方法新建目录,并显示详细执行过程: (1)使用绝对路径在当前目录下创建 new_dir目录 (2)使用相对路径、在当前目录创建dir1、dir2、dir3目录 (3)…...

Mysql 中的两阶段提交
MySQL 中的“两阶段提交”(Two-Phase Commit,2PC)是用于分布式事务中的一种协议,目的是保证在多个数据库节点之间操作的一致性。虽然 MySQL 自身并不是分布式数据库,但在 使用 InnoDB 引擎和 binlog 的情况下ÿ…...

Scade One - 将MBD技术从少数高安全领域向更广泛的安全嵌入式软件普及
Scade One是继Scade Suite version 6自2008年起发展近20年后的首次主要改进版本。在Scade One发布的同时,Scade团队发布了一系列介绍Scade One的博客。本篇Scade One - Democratizing model-based development是其中的一部分。在后面的内容中,将复述博客…...

C# 与 相机连接
一、通过组件连接相机 需要提前在VisionPro里面保存一个CogAcqFifoTool相机工具为 .vpp 定义一个相机工具 CogAcqFifoTool mAcq null;将保存的相机工具放入mAcq中 string path “C:\Acq.vpp”; mAcq (CogAcqFifoTool)CogSerializer.LoadObjectFrommFile(path);给窗口相机…...

JAVA学习小记之IO流04--转换流篇
转换流: 按照A规则存储,同样按照A规则解析,那么就能显示正确的文本符号。反之,按照A规则存储,再按照B规则解析,就会导致乱码现象。 转换的原因是: 有的文件并非是按UTF-8编码,那么在读文件内容…...

SH 和 BASH 有什么不同 ?
当谈到 shell 脚本编写时,经常出现两个突出的 shell,Bourne shell (SH) 和 Bourne Again shell (Bash)。两者都是基于 unix 和 linux 的系统的组成部分,提供与操作系统交互的接口。本文旨在深入研究这两种 shell 之间的复杂差异,揭…...

linux专题3-----linux上链接远程mysql
要在 Ubuntu 上连接远程 MySQL 数据库,你可以使用 MySQL 客户端工具或者其他数据库管理工具,如 phpMyAdmin 或 MySQL Workbench。以下是使用 MySQL 命令行工具连接远程 MySQL 的步骤: 确保已安装 MySQL 客户端 首先,确保你的 Ub…...

Qt 音乐播放器项目
具体代码见:https://gitee.com/Suinnnnnn/MusicPlayer 文章目录 0. 预备1. 界面1.1 各部位长度1.2 ui文件1.3 窗口前置设置1.4 设置QSS 2. 自定义控件2.1 按钮2.2 推荐页面2.3 CommonPage2.4 滑杆 3. 音乐管理4. 歌词界面4.1 ui文件4.2 LrcPage.h文件 5. 音乐播放控…...

类似于langchain的开发框架有哪些?
类似于 LangChain 的开发框架主要用于构建基于大语言模型(LLM)的应用程序,提供链式调用、工具集成、记忆管理等功能。以下是一些类似的框架和工具: 1. LlamaIndex(原GPT Index) 特点:专注于文档…...
