算法-- js排序
汇总
注:以下log n 是 O(log2n)
 注:快速排序实际应用中通常最优,但需避免最坏情况。
注:快速排序实际应用中通常最优,但需避免最坏情况。
1 快速排序
[快速排序的思路]
- 分区:从数组中任意选择一个“基准”,所有比基准小的元素放在基准前面,比基准大的元素放在基准的后面。
- 递归:递归地对基准前后的子数组进行分区。
[快速排序]
- 时间复杂度:
时间复杂度:最优/平均情况O(n*logN), 最坏情况O(n^2)。
n*logN: 当每次划分能大致将数组分为两部分时(如基准值选择接近中位数),递归深度为 logn,每层处理 n 个元素
n^2: 当数组已有序或基准值总是极值(如第一个或最后一个元素),导致每次划分仅减少一个元素,递归深度为 nPS:递归的时间复杂度是O(logN)。(劈成两半,递归前left后right,基本劈成两半递归的操作都是logN)
分区操作的时间复杂度是O(n)。- 空间复杂度:O(logN)(递归造成的栈空间的使用)//没明白为什么递归深度是 logn?--简单来说是:"拆分两半"这个动作log2 n次
答:快速排序的递归深度为logn是因为在理想情况下(每次划分都能将数组均匀分成两部分),递归树的深度与二分查找类似。以下是具体解释:
均匀划分的数学原理每次划分后,数组被分成两个子数组,长度约为2n。递归调用会持续将子数组对半分割,直到子数组长度为1。此时递归深度d满足:
n/(2^d)=1 ⟹ d=log2 n
因此深度为O(logn)function quickSort(arr) {// 递归终止条件:数组长度 ≤1 时直接返回/* 这里也说明一下 为啥要 小于等于1 , 因为有可能 出现左边数组为空的情况 ,不能是 ==1 那样就会出现 程序崩溃的情况 , 这样==0时没有return值也就是递归不会结束所以报错Maximum call stack size exceeded */if (arr.length <= 1) {return arr;}const left = [];const right = [];const pivot = arr[0]; // 基准值取第一个元素// 从第二个元素开始遍历(避免越界)for (let i = 1; i < arr.length; i++) {if (arr[i] < pivot) {left.push(arr[i]);} else {right.push(arr[i]);}}// 递归处理左右子数组,拼接结果return [...quickSort(left), pivot, ...quickSort(right)];
}// 使用示例
const arr = [2, 4, 5, 3, 1];
const sortedArr = quickSort(arr);
console.log(sortedArr); // 输出: [1, 2, 3, 4, 5]
2 冒泡排序
[冒泡排序的思路]
- 比较所有的相邻元素,如果第一个比第二个大,则交换它们。
- 一轮下来,可以保证最后一个数是最大的。
- 执行n-1轮,就可以完成排序。
[冒泡排序]
- 时间复杂度
1.两个嵌套循环
2.时间复杂度:O(n^2)--这个时间复杂度是不太好的排序时间复杂度
- 空间复杂度:O(1)
function bubbleSort(arr) {// 先写第一轮冒泡;// 另外注意:arr.length-1// for (let j = 0; j < arr.length-1; j++) {// if (arr[j] > arr[j + 1]) {// let temp = arr[j]// arr[j] = arr[j + 1]// arr[j + 1] = temp// }// }// 多轮冒泡for (let i = arr.length - 1; i > 0; i--) {for (let j = 0; j < i; j++) {if (arr[j] > arr[j + 1]) {let temp = arr[j]arr[j] = arr[j + 1]arr[j + 1] = temp}}}return arr
}
let arr = [2, 4, 3, 5, 1]
let res = bubbleSort(arr)
console.log('res:', res)
3 插入排序
[插入排序的思路]
- 初始化:将第一个元素视为已排序序列。
- 插入过程
- 待插入元素暂存temp=arr[i]:从第二个元素(ax)开始,暂存其值为temp。
- 大数后移:向前扫描:从 ax 的前一个元素开始反向遍历,将所有大于 temp 的元素后移一位。
- 插入位置:当遇到第一个小于等于 temp 的元素 ay 时,将 temp 插入到 ay 的后面。
- 重复:对后续所有未排序元素执行上述操作。
[插入排序]
- 时间复杂度
1.两个嵌套循环。
2.时间复杂度:O(n^2)。空间复杂度:
-空间复杂度:O(1)
原因:仅需常数级别的额外空间(如临时变量temp),属于原地排序算法function insertSort(arr) {for (let i = 1; i < arr.length; i++) {const temp = arr[i] // 待插入元素let j = i // 移动索引while (j > 0) {if (arr[j - 1] > temp) {arr[j] = arr[j - 1] // 元素后移j--} else {break;}}arr[j] = temp // 待插入元素-插入到正确位置}return arr
}
let arr = [2, 4, 3, 5, 1]
let res = insertSort(arr)
console.log('res:', res)// ![注意]:这样写会报错,因为j = i + 1、arr[j]会超出范围
// function insertSort(arr) {
// for (let i = 0; i < arr.length; i++) {
// let j = i + 1
// const temp = arr[i]
// while (j > 0) {
// if (arr[j] < temp) {
// arr[j - 1] = arr[j]
// j--
// } else {
// break;
// }
// }
// arr[j] = temp
// }
// return arr
// }
4 选择排序
[选择排序的思路]
- 找到数组中的最小值,选中它并将其放置在第一位。
- 接着找到第二小的值,选中它并将其放置在第二位。
- 以此类推,执行n-1轮。
[选择排序]
- 时间复杂度
两个嵌套循环;时间复杂度:O(n^2)。--性能不太好的排序算法- 时间复杂度:O(1) -- 原地排序
function selectionSort(arr) {for (let i = 0; i < arr.length - 1; i++) {let minIndex = i;// 在未排序部分中寻找最小值for (let j = i + 1; j < arr.length; j++) {if (arr[j] < arr[minIndex]) {minIndex = j;}}// 将最小值交换到已排序部分的末尾if (minIndex !== i) {[arr[i], arr[minIndex]] = [arr[minIndex], arr[i]]; // ES6解构赋值交换}}return arr; // 返回排序后的数组(可选)
}// 使用示例
const arr = [5, 4, 3, 2, 1];
const sortedArr = selectionSort(arr);
console.log(sortedArr); // 输出: [1, 2, 3, 4, 5]
C++排序版本见:算法-- C++排序
相关文章:

算法-- js排序
汇总 注:以下log n 是 O(log2n) 注:快速排序实际应用中通常最优,但需避免最坏情况。 1 快速排序 [快速排序的思路] 分区:从数组中任意选择一个“基准”,所有比基准小的元素放在基准前面,比基准大的元素…...

FfreeRTOS有阻塞作用的API
在 FreeRTOS 中,阻塞 API 是指那些会导致调用任务进入阻塞状态(Blocked State)的函数,即任务会暂时让出 CPU,直到某个条件满足(如超时、信号量可用、队列数据到达等)。以下是常见的阻塞 API 分类及示例: 1. 任务延迟(延时) vTaskDelay() 使任务阻塞指定的时间(以系统…...
·棒球1号位)
【棒垒球规则】全国幼儿软式棒垒球比赛规则(三)·棒球1号位
棒垒球球队的组成 3.01球队的组成 球队由教练员及工作人员 2 名至 4 名、队员 9 至 12 名组成。 球衣背号不大于两位数,背号不小于 15 厘米。 上场队员名单应填写上场选手和替补选手。 3.02防守位置及名称(参照图四) a.9 名队…...
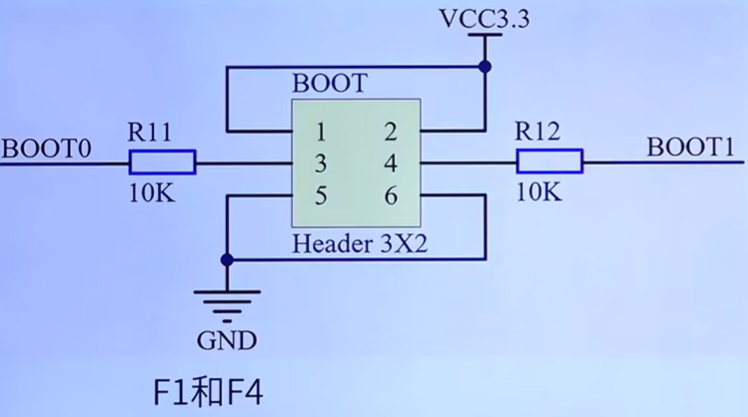
stm32week10
stm32学习 七.CAN 7.STM32 CAN外设 标识符过滤器: 每个过滤器的核心由两个32位寄存器组成:R1[31:0]和R2[31:0] FSCx:位宽设置,置0为16位,置1为32位 FBMx:模式设置,置0为屏蔽模式,…...

Linux上历史命令显示时间,修改时间戳
今天分享一个生产环境避免背锅的小技巧:设置历史命令执行的具体时间。还可以快速定位问题出现的时间点并恢复误操作导致的系统问题,用于追踪溯源。 在Linux系统中,默认情况下,history命令只会显示命令的编号和命令内容࿰…...

看雪 get_pwn3(2016 CCTF 中的 pwn3)
get_pwn3(2016 CCTF 中的 pwn3) 格式化字符串漏洞 get_pwn3(2016 CCTF 中的 pwn3) (1) motalymotaly-VMware-Virtual-Platform:~/桌面$ file pwn3 pwn3: ELF 32-bit LSB executable, Intel 80386, version 1 (SYSV), dynamically linked, interpreter /lib/ld-linux.so.2, …...

python全栈-JavaScript
python全栈-js 文章目录 js基础变量与常量JavaScript引入到HTML文件中JavaScript注释与常见输出方式 数据类型typeof 显示数据类型算数运算符之加法运算符运算符之算术运算符运算符之赋值运算符运算符之比较运算符运算符之布尔运算符运算符之位运算符运算符优先级类型转换 控制…...

操作系统概述(3)
批处理系统 1.单道批处理系统 单道批处理系统是成批地处理作用,并且始终只有一道作业在内存中的系统。优点:提高系统资源的利用率和系统吞吐量。缺点:系统中的资源得不到充分利用。 2.多道批处理系统 引入多道程序设计技术,是…...

SolidWorks2025三维计算机辅助设计(3D CAD)软件超详细图文安装教程(2025最新版保姆级教程)
目录 前言 一、SolidWorks下载 二、SolidWorks安装 三、启动SolidWorks 前言 SolidWorks 是一款由法国达索系统(Dassault Systmes)公司开发的三维计算机辅助设计(3D CAD)软件,广泛用于机械设计、工程仿真和产品开…...

powershell绑定按钮事件的两种方式
写一个powershell的简单GUI做本地任务,试验出2个方法: 方法1: function btn1_click {write-host $text1.Text -ForegroundColor Green -BackgroundColor Black }$btn1.Add_Click({btn1_click})方法2: $btn2_click {write-host $…...

JBDC Java数据库连接(1)
目录 JDBC概述 定义 JDBC API 实例 JDBC搭建 建立与数据库连接: 形式: 实例 获得Satement执行sql语句 Satement中的方法: 实例 实例 JDBC概述 定义 JDBC(Java DataBase Connectivity)java数据库连接是一种用于执行SQL…...

Spring Boot 3.x 集成 MongoDB 的 默认配置项及默认值,以及 常用需要修改的配置项 的详细说明
以下是 Spring Boot 3.x 集成 MongoDB 的 默认配置项及默认值,以及 常用需要修改的配置项 的详细说明: 一、默认配置项及默认值 Spring Boot 对 MongoDB 的默认配置基于 spring.data.mongodb 前缀,以下是核心配置项: 配置项默认…...

git rebase复杂场景验证
经常面临复杂的分支管理,这里对几种场景的行为做一些验证。 结论总结 git rebase br_name:等价与新建br_name分支,然后找到当前分支与br_name分支的分叉点。然后把分叉点以后的提交(当前分支)一个一个的cherry-pick过…...

【Introduction to Reinforcement Learning】翻译解读2
2.2 马尔可夫决策过程(MDPs) 马尔可夫决策过程(MDP)为顺序决策提供了框架,其中动作不仅影响即时奖励,还会影响未来结果。与多臂老虎机问题不同,MDP中的即时奖励与延迟奖励相平衡。在多臂老虎机…...
Spark部署核弹级避坑指南:从高并发集群调优到源码级安全加固(附万亿级日志分析实战+智能运维巡检系统))
大数据(5)Spark部署核弹级避坑指南:从高并发集群调优到源码级安全加固(附万亿级日志分析实战+智能运维巡检系统)
目录 背景一、Spark核心架构拆解1. 分布式计算五层模型 二、五步军工级部署阶段1:环境核弹级校验阶段2:集群拓扑构建阶段3:黄金配置模板阶段4:高可用启停阶段5:安全加固方案 三、万亿级日志分析实战1. 案例背景&#x…...

Linux内核中TCP协议栈的实现:tcp_close函数的深度剖析
引言 TCP(传输控制协议)作为互联网协议族中的核心协议之一,负责在不可靠的网络层之上提供可靠的、面向连接的字节流服务。Linux内核中的TCP协议栈实现了TCP协议的全部功能,包括连接建立、数据传输、流量控制、拥塞控制以及连接关闭等。本文将深入分析Linux内核中tcp_close…...

从搜索丝滑过渡到动态规划的学习指南
搜索&动态规划 前言砝码称重满分代码及思路solution 1(动态规划)solution 2(BFS) 跳跃满分代码及思路solution 1(动态规划)solution 2 (BFS) 积木画满分代码及思路动态规划思路讲解solution 前言 本文主要是通过一些竞赛真题…...

(一)栈结构、队列结构
01-线性结构-数组-栈结构 线性结构(Linear List)是由n(n>0)个数据元素(结点) a[0], a[1], a[2], a[3],...,a[n-1]组成的有限序列 数组 通常数组的内存是连续的,所以在知道数组下标的情况下,访问效率是…...

AWS SNS深度解析:构建高可用、可扩展的云原生消息通信解决方案
引言 在云原生架构中,高效的消息通信是系统解耦、实时响应的核心需求。AWS Simple Notification Service(SNS)作为一款全托管的发布/订阅(Pub/Sub)服务,为开发者提供了灵活、可靠的消息分发能力。本文将从…...

MySQL基础 [五] - 表的增删查改
目录 Create(insert) Retrieve(select) where条件 编辑 NULL的查询 结果排序(order by) 筛选分页结果 (limit) Update Delete 删除表 截断表(truncate) 插入查询结果(insertselect&…...

4.7学习总结 可变参数+集合工具类Collections+不可变集合
可变参数: 示例: public class test {public static void main(String[] args) {int sumgetSum(1,2,3,4,5,6,7,8,9,10);System.out.println(sum);}public static int getSum(int...arr){int sum0;for(int i:arr){sumi;}return sum;} } 细节:…...

OpenGL学习笔记(简介、三角形、着色器、纹理、坐标系统、摄像机)
目录 简介核心模式与立即渲染模式状态机对象GLFW和GLAD Hello OpenGLTriangle 三角形顶点缓冲对象 VBO顶点数组对象 VAO元素缓冲对象 EBO/ 索引缓冲对象 IEO 着色器GLSL数据类型输入输出Uniform 纹理纹理过滤Mipmap 多级渐远纹理实际使用方式纹理单元 坐标系统裁剪空间 摄像机自…...

vmware虚拟机上Ubuntu或者其他系统无法联网的解决方法
一、检查虚拟机是否开启了网络服务 打开方式:控制面板->-管理工具--->服务 查找 VMware DHCP Service 和VMware NAT Service ,确保这两个服务已经启动。如下图,没有启动就点击启动。 二、设置网络类型 我们一般使用前两种多一些&…...

OpenVLA-OFT——微调VLA时加快推理的三大关键设计:支持动作分块的并行解码、连续动作表示以及L1回归(含输入灵活化及对指令遵循的加强)
前言 25年3.26日,这是一个值得纪念的日子,这一天,我司「七月在线」的定位正式升级为了:具身智能的场景落地与定制开发商 ,后续则从定制开发 逐步过渡到 标准产品化 比如25年q2起,在定制开发之外࿰…...

Linux脚本基础详解
一、基础知识 Linux 脚本主要是指在 Linux 系统中编写的用于自动化执行任务的脚本程序,其中最常用的便是 Bash 脚本。下面我们将从语法、使用方法和示例三个方面详细讲解 Linux 脚本。 1. 脚本简介 定义:Linux 脚本是一系列命令的集合,可以…...

LabVIEW 油井动液面在线监测系统
项目背景 传统油井动液面测量依赖人工现场操作,面临成本高、效率低、安全风险大等问题。尤其在偏远地区或复杂工况下,测量准确性与时效性难以保障。本系统通过LabVIEW虚拟仪器技术实现硬件与软件深度融合,为油田智能化转型提供实时连续监测解…...

泛微ECOLOGY9 解决文档中打开发票类PDF文件无内容的配置方法
解决文档中打开发票类PDF文件无内容的配置方法 情况如下: 如果OA文档中打开的PDF文件如下图这样空白的,那么可以试试下面的方法进行解决。 解决方法: 在OA安装目录中找到 ecology/WEB-INF/prop/docpreview.properties 配置文件ÿ…...

大模型RAG项目实战-知识库问答助手v1版
安装 Ollama 根据官网指导,安装对应版本即可。 下载安装指导文档: handy-ollama/docs/C1/1. Ollama 介绍.md at main datawhalechina/handy-ollama 注意:在 Windows 下安装 Ollama 后,强烈建议通过配置环境变量来修改模型存储…...

统计子矩阵
1.统计子矩阵 - 蓝桥云课 统计子矩阵 问题描述 给定一个 NM 的矩阵 A,请你统计有多少个子矩阵(最小 11,最大 NM)满足子矩阵中所有数的和不超过给定的整数 K? 输入格式 第一行包含三个整数 N,M 和 K。 …...

Vue.js 实现下载模板和导入模板、数据比对功能核心实现。
在前端开发中,数据比对是一个常见需求,尤其在资产管理等场景中。本文将基于 Vue.js 和 Element UI,通过一个简化的代码示例,展示如何实现“新建比对”和“开始比对”功能的核心部分。 一、功能简介 我们将聚焦两个核心功能&…...
