Python 实现的运筹优化系统数学建模详解(最大最小化模型)
一、引言
在数学建模的实际应用里,最大最小化模型是一种极为关键的优化模型。它的核心目标是找出一组决策变量,让多个目标函数值里的最大值尽可能小。该模型在诸多领域,如资源分配、选址规划等,都有广泛的应用。本文将深入剖析最大最小化模型的原理、算法实现,详细解读其 Python 代码,并探讨它在不同场景下的应用。
二、最大最小化模型原理
2.1 模型描述
最大最小化模型的一般形式可表示为:
\(\min_{x} \max_{i} f_i(x)\)
其中,x 为决策变量向量,\(f_i(x)\) 是关于 x 的一组函数,\(i = 1,2,\cdots,n\)。我们的目标是找到一个合适的 x 值,使得所有 \(f_i(x)\) 中的最大值达到最小。
2.2 约束条件
在实际问题中,决策变量 x 通常要满足一定的约束条件,例如:
\(lb_j \leq x_j \leq ub_j, \quad j = 1,2,\cdots,m\)
这里,\(lb_j\) 和 \(ub_j\) 分别是决策变量 \(x_j\) 的下限和上限。
三、最大最小化模型的算法实现讲解
3.1 转化为标准优化问题
最大最小化模型 \(\min_{x} \max_{i} f_i(x)\) 可以通过引入一个额外的变量 t 转化为一个等价的标准优化问题:
\(\begin{align*} \min_{x,t} &\quad t \\ \text{s.t.} &\quad f_i(x) \leq t, \quad i = 1,2,\cdots,n \\ & \quad lb_j \leq x_j \leq ub_j, \quad j = 1,2,\cdots,m \end{align*}\)
在这个转化后的问题中,我们引入了一个新的变量 t 来表示所有 \(f_i(x)\) 的最大值。约束条件 \(f_i(x) \leq t\) 保证了 t 确实是所有 \(f_i(x)\) 的上界,而目标是最小化 t,这样就找到了满足条件的最小最大值。
3.2 选择优化算法
对于转化后的标准优化问题,可以使用多种优化算法进行求解。常见的算法包括:
- 序列最小二乘法(Sequential Least Squares Programming, SLSQP):这是一种迭代算法,适用于有约束的非线性优化问题。它通过不断迭代更新决策变量的值,逐步逼近最优解。在每次迭代中,它会求解一个二次规划子问题来确定搜索方向。
- 内点法(Interior Point Method):也是一种常用于求解有约束优化问题的算法。它通过在可行域内部搜索最优解,避免了在边界上可能遇到的数值不稳定问题。
3.3 迭代求解过程
以 SLSQP 算法为例,其迭代求解过程大致如下:
- 初始化:给定决策变量 x 和额外变量 t 的初始值 \(x^0\) 和 \(t^0\)。
- 计算目标函数和约束条件的值:在每次迭代中,计算当前决策变量下的目标函数值 t 和所有约束条件 \(f_i(x) - t\) 的值。
- 求解二次规划子问题:根据当前的目标函数和约束条件的梯度信息,构建一个二次规划子问题,并求解该子问题得到搜索方向。
- 更新决策变量:沿着搜索方向更新决策变量 x 和 t 的值。
- 判断收敛条件:检查是否满足收敛条件,如目标函数值的变化小于某个阈值,或者决策变量的变化小于某个阈值。如果满足收敛条件,则停止迭代,输出最优解;否则,返回步骤 2 继续迭代。
四、代码详细解析
4.1 导入必要的库
import numpy as np
from scipy.optimize import minimize
numpy是 Python 中用于科学计算的基础库,提供了高效的数组操作和数学函数。在代码中,我们使用numpy来处理数组数据,例如创建数组、进行数组运算等。scipy.optimize.minimize是一个用于求解最小化问题的函数,我们将使用它来求解最大最小化模型。
4.2 定义目标函数
# 目标函数
def obj_func(x, a, b):f = np.zeros(len(a))for i in range(len(a)):f[i] = np.abs(x[0] - a[i]) + np.abs(x[1] - b[i])return f
obj_func函数接受三个参数:x是决策变量向量,a和b是用户输入的数组。- 函数内部创建了一个长度为
len(a)的零数组f,用于存储每个目标函数值。 - 通过循环计算每个 \(f_i(x)\) 的值,这里的 \(f_i(x)\) 定义为 \(|x_0 - a_i| + |x_1 - b_i|\),其中 \(a_i\) 和 \(b_i\) 是数组
a和b中的元素。 - 最后返回存储所有目标函数值的数组
f。
4.3 定义总的目标函数
# 总的目标函数,取目标函数值数组中的最大值
def overall_objective(x, a, b):return np.max(obj_func(x, a, b))
overall_objective函数接受三个参数:x是决策变量向量,a和b是用户输入的数组。- 函数内部调用
obj_func函数计算每个目标函数值,然后使用np.max函数取这些值中的最大值,这个最大值就是我们要最小化的目标。
4.4 获取用户输入
# 获取用户输入
def get_user_input():a_input = input("请输入 a 数组的值,用逗号分隔:")a = np.array([float(i) for i in a_input.split(',')])b_input = input("请输入 b 数组的值,用逗号分隔:")b = np.array([float(i) for i in b_input.split(',')])x0_input = input("请输入初始值 x0,用逗号分隔(两个值):")x0 = np.array([float(i) for i in x0_input.split(',')])lb_input = input("请输入决策变量的下限 lb,用逗号分隔(两个值):")lb = np.array([float(i) for i in lb_input.split(',')])ub_input = input("请输入决策变量的上限 ub,用逗号分隔(两个值):")ub = np.array([float(i) for i in ub_input.split(',')])return a, b, x0, lb, ub
get_user_input函数用于获取用户输入的数据。- 依次提示用户输入
a数组、b数组、初始值x0、决策变量的下限lb和上限ub。 - 使用
input函数获取用户输入的字符串,然后使用split(',')方法将字符串按逗号分隔成列表,再将列表中的每个元素转换为浮点数,最后使用np.array函数将列表转换为numpy数组。 - 最后返回这些数组。
4.5 主函数
# 主函数
def main():a, b, x0, lb, ub = get_user_input()bounds = [(lb[0], ub[0]), (lb[1], ub[1])]result = minimize(fun=overall_objective, x0=x0, args=(a, b), method='SLSQP', bounds=bounds)print("优化后的决策变量值:", result.x)print("每个 f_i(x) 的值:", obj_func(result.x, a, b))print("目标函数的最小值:", np.max(obj_func(result.x, a, b)))
main函数是程序的入口点。- 调用
get_user_input函数获取用户输入的数据。 - 根据用户输入的下限
lb和上限ub创建约束条件bounds。 - 使用
scipy.optimize.minimize函数进行优化求解。fun=overall_objective指定要最小化的目标函数,x0=x0指定初始值,args=(a, b)传递额外的参数a和b给目标函数,method='SLSQP'指定使用的优化算法为序列最小二乘法(Sequential Least Squares Programming),bounds=bounds指定约束条件。 - 最后输出优化后的决策变量值、每个 \(f_i(x)\) 的值和目标函数的最小值。
4.6 程序入口
if __name__ == "__main__":main()
- 这是 Python 程序的标准入口,确保
main函数只在直接运行该脚本时被调用。
4.7 代码使用方法
- 运行代码后,程序会提示你输入
a数组的值,用逗号分隔。例如:1,4,3,5,9,12,6,20,17,8。 - 接着,程序会提示你输入
b数组的值,同样用逗号分隔。例如:2,10,8,18,1,4,5,10,8,9。 - 然后,程序会提示你输入初始值
x0,用逗号分隔两个值。例如:6,6。 - 再接着,程序会提示你输入决策变量的下限
lb,用逗号分隔两个值。例如:3,4。 - 最后,程序会提示你输入决策变量的上限
ub,用逗号分隔两个值。例如:8,10。 - 程序会根据你输入的数据进行优化求解,并输出优化后的决策变量值、每个 \(f_i(x)\) 的值和目标函数的最小值。
五、最大最小化模型在数学建模中的应用场景
5.1 选址问题
在选址问题中,我们常常需要找到一个合适的位置,使得该位置到各个需求点的最大距离最小。例如,在城市中选择一个消防站的位置,我们希望这个消防站到城市中各个区域的最大响应时间最短;或者选择一个物流中心的位置,使得该物流中心到各个配送点的最大运输距离最小。
5.2 资源分配问题
在资源分配问题中,我们可能需要将有限的资源分配给多个任务,使得各个任务之间的最大资源消耗最小。例如,在项目管理中,我们需要将人力、物力等资源分配给多个项目,使得每个项目的最大资源短缺最小;或者在电力分配中,将发电资源分配给多个用户,使得各个用户的最大电力不足最小。
5.3 可靠性设计问题
在可靠性设计中,我们希望设计一个系统,使得系统中各个组件的最大失效风险最小。例如,在设计一个电子电路时,我们需要选择合适的元件和布局,使得各个元件的最大故障概率最小;或者在设计一个机械结构时,我们需要选择合适的材料和尺寸,使得各个部件的最大损坏风险最小。
总之,最大最小化模型在许多实际问题中都有重要的应用,通过合理地构建模型和使用优化算法,我们可以找到最优的解决方案。
相关文章:
)
Python 实现的运筹优化系统数学建模详解(最大最小化模型)
一、引言 在数学建模的实际应用里,最大最小化模型是一种极为关键的优化模型。它的核心目标是找出一组决策变量,让多个目标函数值里的最大值尽可能小。该模型在诸多领域,如资源分配、选址规划等,都有广泛的应用。本文将深入剖析最大…...

网络安全·第二天·ARP协议安全分析
今天我们来考虑考虑计算机网络中的一类很重要的协议-------ARP协议,介绍他用途的同时,分析分析ARP协议存在的一些漏洞及其相关的协议问题。 一、物理地址与IP地址 1、举例 在计算机网络中,有两类地址十分关键,一类称为物理地址&a…...

Python设计模式:命令模式
1. 什么是命令模式? 命令模式是一种行为设计模式,它将请求封装为一个对象,从而使您能够使用不同的请求、队列或日志请求,以及支持可撤销操作。 命令模式的核心思想是将请求的发送者与请求的接收者解耦,使得两者之间的…...
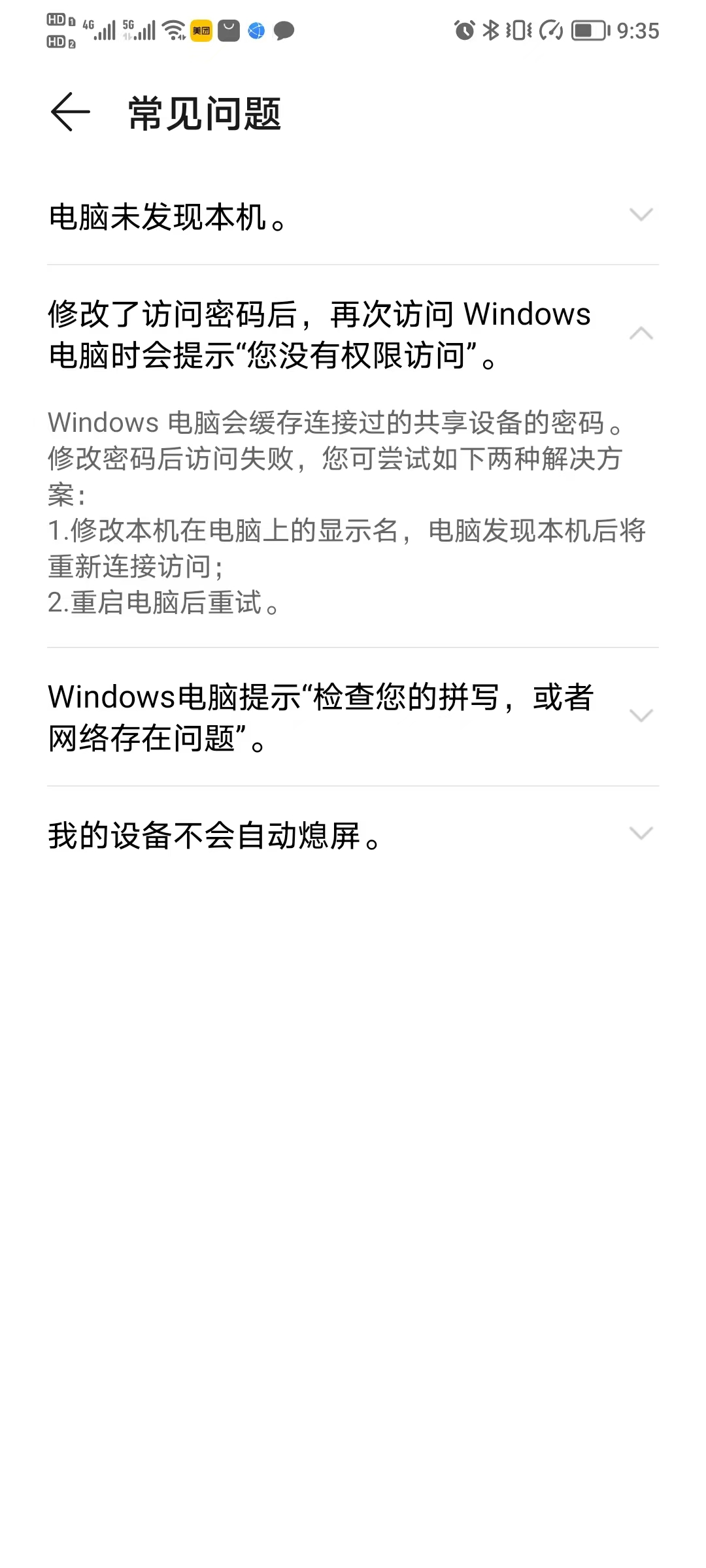
华为手机或平板与电脑实现文件共享
1.手机或平板与电脑在同一个网络 2.打开手机或平板端,设置---更多连接----快分享或华为分享打开此功能-----开启共享至电脑 3.打开电脑,网络中就可看到手机端分享的用户名称 4. 登陆就可访问手机 5.常见问题 5.1 电脑未发现本机 5.2 修改了访问密码后再…...

幻兽帕鲁(Palworld)在线工具集:让游戏体验更轻松!
幻兽帕鲁(Palworld)在线工具集:让游戏体验更轻松! 🎮 工具介绍 为了帮助广大幻兽帕鲁玩家更好地享受游戏,我开发了这个全面的在线工具集。无需下载安装,打开网页即可使用,完全免费! …...

学习51单片机Day02---实验:点亮一个LED灯
目录 1.先看原理图 2.思考一下(sbit的使用): 3.给0是要让这个LED亮(LED端口设置为低电平) 4.完成的代码 1.先看原理图 比如我们要让LED3亮起来,对应的是P2^2。 2.思考一下(sbit的使用&…...

【Kubernetes】Kubernetes 如何进行日志管理?Fluentd / Loki / ELK 适用于什么场景?
由于 Kubernetes 运行在容器化的环境中,应用程序和系统日志通常分布在多个容器和节点上,传统的日志管理方法(例如直接访问每个节点的日志文件)在 Kubernetes 中不适用。 因此,Kubernetes 引入了集中式日志管理方案&am…...
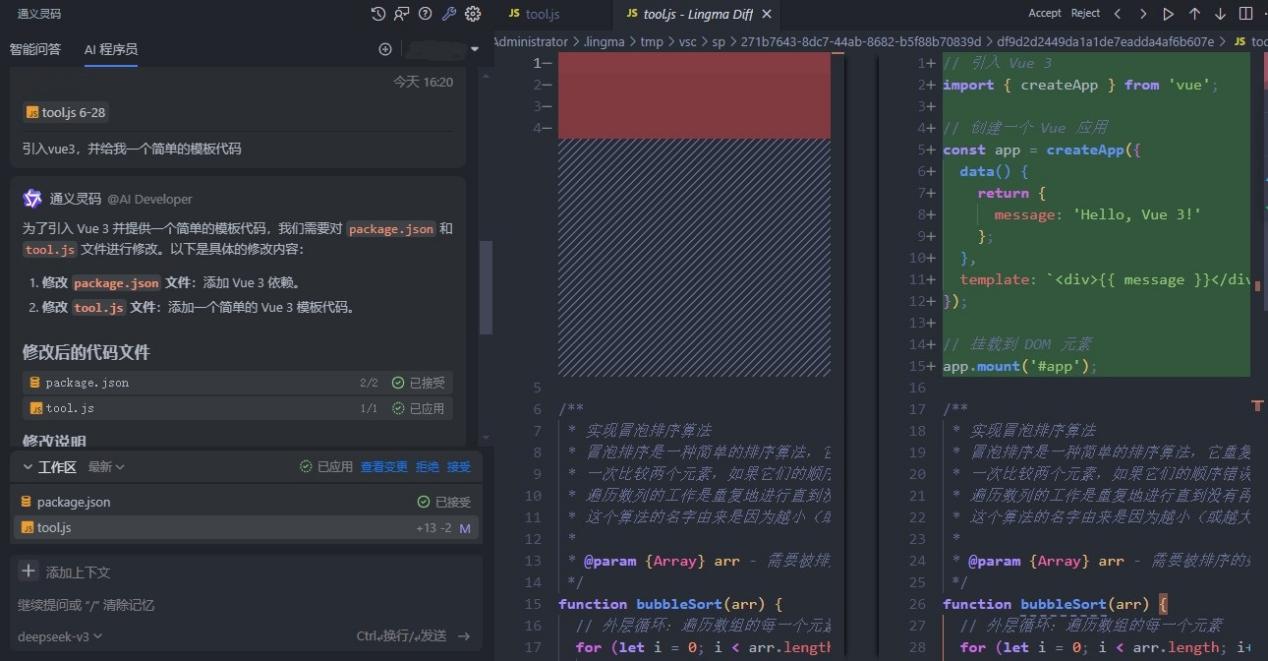
如何使用通义灵码学习JavaScript和DOM
如果你看到了本手册的页面数量,你就会发现JavaScript的API真的非常丰富,在MDN上专门有一大分类用于介绍JavaScript的API,但软件工程行业有一个著名法则叫2-8法则,意思是只有20%的内容会经常使用到,而80%的内容只在一些…...

Elasticsearch8.x集成SpringBoot3.x
Elasticsearch8.x集成SpringBoot3.x 配置项目引入依赖添加配置文件导入ca证书到项目中添加配置 实战操作创建mapping创建文档查询更新全量更新删除数据批量操作(bulk)基本搜索复杂布尔搜索嵌套(nested)搜索分页查询滚动分页查询After分页查询词条(terms)聚合日期聚合 配置项目 …...

基于labview的多功能数据采集系统
基于labview的多功能数据采集系统(可定制功能) 包含基于NI温度采集卡。电流采集卡。电压采集卡的数据采集功能 数据存储 报表存储 数据处理与分析 生产者消费者架构 有需要可联系...

250410异常记事
今天遇到一件极坑的事情,关于uni.setStorageSync: Invalid args: type check failed for args “key”. Expected String, got Boolean with value true. 项目是网上下的一个element-plus、uniapp 混搭的框架https://ext.dcloud.net.cn/plugin?id16396 异常代码如…...

小程序租赁系统源码功能分享
系统架构图解:技术栈与业务流程 设备租赁系统的架构可以分为三个主要部分:后台服务(SpringBoot MyBatisPlus MySQL)、用户端与师傅端(UniApp)、以及管理后台(Vue ElementUI)。下…...

30天学Java第八天——设计模式
装饰器模式 Decorator Pattern 装饰器模式(Decorator Pattern)是一种结构型设计模式,它允许通过动态地添加功能来扩展对象的行为,而不需要修改原有的类。 这种模式通常用于增强对象的功能,与继承相比,使用…...

Linux 调试代码工具:gdb
文章目录 一、debug vs release:两种程序形态的本质差异1. 什么是 debug 与 release?2. 核心差异对比 二、为什么需要 debug:从项目生命周期看调试价值1. 项目开发流程中的调试闭环(流程图示意)2. Debug 的核心意义与目…...

SpringMVC基础一(SpringMVC运行原理)
先了解MVC,在JavaWeb基础五中。 回忆servlet,在javaweb基础二中。 创建一个web项目: 1、新建maven项目,导入依赖。(junit、springmvc、spring-webmvc、servlet-api、jsp-api、jstl) <groupId>org…...

Java权限修饰符深度解析
Java权限修饰符深度解析与最佳实践 一、权限修饰符总览 Java提供四种访问控制修饰符,按访问范围从宽到窄排序如下: 修饰符类内部同包类不同包子类全局范围public✔️✔️✔️✔️protected✔️✔️✔️❌默认(无)✔️✔️❌❌pr…...

Springboot JPA ShardingSphere 根据年分表
Spring Boot集成JPA与ShardingSphere实现按年分表,需重点关注分片算法选择、时间字段映射及动态表管理。以下是实现方案: 一、依赖配置 1. 核心依赖引入 <!-- ShardingSphere JDBC --> <dependency><groupId>org.apache.shardi…...

uniapp小程序生成海报/图片并保存分享
调研结果: 方法一:canvasuni.canvasToTempFilePath耗时太长,现在卡在canvas的绘制有问题,canvas绘制的部分东西不生效但是找不到原因 方法二:使用wxml-to-canvas其实也差不多是用canvas手动绘制,可能会卡在…...

蓝桥杯刷题--宝石组合
在一个神秘的森林里,住着一个小精灵名叫小蓝。有一天,他偶然发现了一个隐藏在树洞里的宝藏,里面装满了闪烁着美丽光芒的宝石。这些宝石都有着不同的颜色和形状,但最引人注目的是它们各自独特的 “闪亮度” 属性。每颗宝石都有一个…...

红宝书第三十一讲:通俗易懂的包管理器指南:npm 与 Yarn
红宝书第三十一讲:通俗易懂的包管理器指南:npm 与 Yarn 资料取自《JavaScript高级程序设计(第5版)》。 查看总目录:红宝书学习大纲 一、基础概念 包管理器:帮你自动下载和管理第三方代码库(如…...

进程状态的转换
进程处于运行态时,它必须已获得所需的资源,在运行结束后就撤销。只有在时间片到或出现了比现在进程优先级更高的进程时才转变成就绪态。 就绪 → 运行 触发条件:进程被调度器选中(如时间片轮转或优先级调度&…...

SpringAOP新链浅析
前言 在复现CCSSSC软件攻防赛的时候发现需要打SpringAOP链子,于是跟着前人的文章自己动手调试了一下 参考了大佬的文章 https://gsbp0.github.io/post/springaop/#%E6%B5%81%E7%A8%8B https://mp.weixin.qq.com/s/oQ1mFohc332v8U1yA7RaMQ 正文 依赖于Spring-AO…...

【动手学深度学习】现代卷积神经网络:ALexNet
【动手学深度学习】现代卷积神经网络:ALexNet 1,ALexNet简介2,AlexNet和LeNet的对比3, AlexNet模型详细设计4,AlexNet采用ReLU激活函数4.1,ReLU激活函数4.2,sigmoid激活函数4.3,为什…...

PyTorch深度学习框架60天进阶学习计划 - 第37天:元学习框架
PyTorch深度学习框架60天进阶学习计划 - 第37天:元学习框架 嘿,朋友们!欢迎来到我们PyTorch进阶之旅的第37天。今天我们将深入探索一个非常有趣且强大的领域——元学习(Meta-Learning),也被称为"学会学习"(Learning to…...

【中检在线-注册安全分析报告】
前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 1. 暴力破解密码,造成用户信息泄露 2. 短信盗刷的安全问题,影响业务及导致用户投诉 3. 带来经济损失,尤其是后付费客户,风险巨大,造…...

UE5 运行时动态将玩家手部模型设置为相机的子物体
在编辑器里,我们虽然可以手动添加相机,但是无法将网格体设置为相机的子物体,只能将相机设置为网格体的子物体 但是为了使用方便,我们希望将网格体设置为相机的子物体,这样我们直接旋转相机就可以旋转网格体࿰…...

EasyExcel-一款好用的excel生成工具
EasyExcel是一款处理excel的工具类,主要特点如下(官方): 特点 高性能读写:FastExcel 专注于性能优化,能够高效处理大规模的 Excel 数据。相比一些传统的 Excel 处理库,它能显著降低内存占用。…...

WEB攻防-Java安全JNDIRMILDAP五大不安全组件RCE执行不出网不回显
目录 1. RCE执行-5大类函数调用 1.1 Runtime方式 1.2 Groovy执行命令 1.3 脚本引擎代码注入 1.4 ProcessImpl 1.5 ProcessBuilder 2. JNDI注入(RCE)-RMI&LDAP&高版本 2.1 RMI服务中的JNDI注入场景 2.2 LDAP服务中的JNDI注入场景 攻击路径示例&#…...

UML组件图
一、UML 组件图 组件图(Component Diagram)主要用于描述系统的物理结构,用于展示可独立部署的软件模块(如微服务、动态链接库、API网关)及其交互关系。组件图中的主要元素包括: 组件(Component…...

DrissionPage移动端自动化:从H5到原生App的跨界测试
一、移动端自动化测试的挑战与机遇 移动端测试面临多维度挑战: 设备碎片化:Android/iOS版本、屏幕分辨率差异 混合应用架构:H5页面与原生组件的深度耦合 交互复杂性:多点触控、手势操作、传感器模拟 性能监控:内存…...
