”插入排序“”选择排序“
文章目录
- 插入排序
- 1. 直接插入排序(O(n^2))
- 举例1:
- 举例2:
- 直插排序的"代码"
- 直插排序的“时间复杂度”
- 2. 希尔排序(O(n^1.3))
- 方法一
- 方法二(时间复杂度更优)
- 选择排序
- 堆排序
- 直接选择排序
我们学过冒泡排序,堆排序等等。(回顾一下:排升序,建大堆;排降序,建小堆。)
排序:所谓排序,就是使⼀串记录,按照其中的某个或某些关键字的⼤⼩,递增或递减的排列起来的
操作。
在生活中也会遇到很多排序:购物筛选排序(按照价格、综合、销量、距离等排序)、百度热搜(根据热搜程度)、院校排名等等。

插入排序
1. 直接插入排序(O(n^2))
基本思想:将(待排序的记录)按照(关键码值的大小)逐个插入到(已经排好序的有序队列)中。直到所有的记录插入完为止,得到一个新的有序序列。
先将arr[end]指向:(有序队列的最后一个数据),然后将(需要和有序数据进行比较的数据:即arr[end+1])暂时存储在tmp中,接下来将arr[end]和tmp里的数据进行比较。

注意在一次循环中,tmp的值是不变的(除非end++,才会使tmp的值改变(tmp=arr[end]))
举例1:
【假设想要排升序】

- 现在arr[end]的值大于tmp,应该排在后面,所以现在将end的值放在end+1的位置,这个时候会发现end+1位置的值被覆盖了,所以我们需要提前将它的值存储在tmp中(这就是将值存储在tmp中的原因)。接下来需要将tmp的值放在end的位置(这个是arr[end]的前面没有其他值的情况,我们可以直接将tmp的值赋给arr[end])
在交换值之后,将end++,tmp的值为arr[end+1] (它不用修改,因为end已经修改了)

-
如果arr[end]<tmp,并不需要交换呢?(比如5和9)那就直接end++,紧接着tmp的值也变啦。
-
紧接着又是将9和6交换,按照之前的方法(将arr[end]的值赋给arr[end+1],然后将tmp的值赋给arr[end]

-
为什么我们还需要将交换之后的arr[end]的值和这个序列前面的值比较呢?------防止它比前面已经排好序的值小
接下来按照前面的方法,再将9和2进行比较
举例2:

直插排序的"代码"
我们需要一个循环来控制end++,往后走;
还需要一个循环来控制:当把arr[end]赋值给arr[end+1]之后,需要将end- -,将前面的数值和tmp继续比较。
在这里插入代码片`void InsertSort(int* arr, int n)
{for (int i = 0; i < n - 1; i++) //为什么是i<n-1?{int end = i;int tmp = arr[end + 1];while (end >= 0){if (arr[end] > tmp){arr[end + 1] = arr[end];end--;}else{break;}}arr[end + 1] = tmp;}
}`

- 为什么是
i<n-1呢?
因为tmp存储的是arr[end+1],我们要确保它是最后一个不会越界,即end+1<n,又因为end=i,所以i+1<n,所以i<n-1。
直插排序的“时间复杂度”
直接插入排序的时间复杂度是O(n^2)
不过O(n^2)是最差的情况。

最差:想将降序----->升序 O(n^2)
最好:升序------->升序 O(n)
2. 希尔排序(O(n^1.3))
希尔排序就是对直接插入排序的一种优化。想要改善降序---->升序的时间复杂度。
希尔排序分为两步:1.预排序 2.直接插入排序
我们可以将很长的一段数组序列变为n段较短的序列,然后对每段“单独”进行直接插入排序(这个叫做预排序)。预排结束之后,小的数据大部分都在前半部分了(只是不按顺序),接着我们再对整体的数组(已经趋于有序的数组)序列进行一次直插排序,这样不仅完成了排序,还优化了时间复杂度。
方法一
- 首先我们需要决定一个值:gap,然后将大段分为n个小段(每段的首和尾相隔gap个元素,即第一个值往后数gap个,那个数据是这段的最后一个元素)。
什么情况下预排:当gap>1的时候
什么情况下整段直插:当gap==1的时候

-
从上图可以知晓:要将一大段数据分为很多组数据,在寻找第二组数据时,需要将上次的首元素下标++。这一步由外层循环控制【遍历每个子序列的起始位置(从 0 到 gap-1)】,
for(i=0;i<gap;i++)(为什么i<gap?) -
接下来是每组数据中,知道了首元素,然后找这组数据中的剩余数据,即end+gap,这个由第二层循环控制:
for(int j=0;j<n-gap;j+=gap);(为什么内层的j<n-gap?) -
再里面的元素之间比较就没有什么特别了,使用的是直接插入排序(它也有循环)。
【gap不能太大(若太大的话,会导致每组的数据比较少,但组数比较多),也不能太小(那样的话每组数据会有很多,那这样的话时间复杂度又变高了)】我们可以让gap由元素个数决定,gap=n/3+1,为什么最后还要+1呢?(如果遇到2/3的情况,那商就是0,也就是gap=0,那间距为0,谁和谁比呢?)而我们最后需要让gap=1,让已经预排之后的整段数据进行直插排序,所以需要+1.
【gap等于多少,这段数据最终就会被分为几组数据】如果n特别特别大,n/3之后也特大,先将+1给忽略掉
-
之前我们说到为什么外层循环中
i<gap而不是i<n呢?

我们第一组数据的第二个元素是arr[end+gap]也就是arr[0+gap],既然arr[gap]在第一组数据中已经进行比较过一次,那之后就没必要再将它比较一次了。大家观察上图会发现每个数据都进行比较过,如果外层用 i < n,会导致重复处理同一子序列,效率降低。 -
还有一个问题是:为什么第二层循环需要
j<n-gap,按照方法一个组中,每个数据它们都相邻gap个(n=8,gap=3第一组元素下标:0,3,6,下标为6的元素后面还有1个元素,但是剩余元素个数不够gap个,那就只能在这次的循环中将后面的元素舍弃。所以在找每组的数据时(即在第二层循环),循环结束的条件是最后一个元素后面的元素个数小于gap个(有剩余的元素或者剩余个数为0(也就是刚好后面没有元素了)),也就是它的下标小于n-gap

第一组的数据:7,4,1
第二组的数据:6,3
第三组的数据:5,2
…
- 然后,先排第一组的数据,再排2,3组的数据
(1)初始情况:arr[end]指向第一个元素,tmp指向(与第一个相隔gap的元素).即tmp=arr[end+gap]
- 若
arr[end]>tmp,那么将arr[end]的值赋给tmp所指向的那个值,即arr[end+gap]=arr[end],赋值之后,将end=end-gap - 若
arr[end]>tmp,不用修改值。直接将end+=gap
对于每组数据的值比较的注释
(2)排完第二组的数据之后,外层的i++,到第二个数据【下标为1】(它作为第二组的首元素),然后进入第二层循环,在进行比较。
到此为止,这个进行了一趟比较
void ShellSort(int* arr, int n)
{int gap = n / 3 + 1;for (int i = 0; i < gap; i++){int j = i;for (j =i; j < n - gap; j += gap){int end = j;int tmp = arr[end + gap];while (end>=0) //将这组数据的每个数据比较,while结束的条件:end>=0;{if (arr[end] > tmp){arr[end + gap] = arr[end];//想继续和前面有序的数据比较,将end-gapend -= gap;}//到这里,arr[end]<tmp,那就不用赋值,直接将下标+gap,tmp的值随之改变,继续比较else {break;}}//在循环中,我们只是将大的数据往后赋值,那当初那个比较小的tmp赋给谁呢?//这组数据如何能比较结束(break)呢?肯定是此时的arr[end]并没有tmp大,不需要交换了//所以,我们把tmp值赋值给之前一个比较的值(由于是end-=gap,所以上一个是end+gap)arr[end + gap] = tmp;}}
}


之后我们将gap不断缩小,继续比较,直至最后gap==1时,进行最后的,对整段进行直插

void ShellSort(int* arr, int n)
{int gap = n;while (gap>1){gap = gap / 3 + 1;for (int i = 0; i < gap; i++){int j = i;for (j = i; j < n - gap; j += gap){int end = j;int tmp = arr[end + gap];while (end >= 0) //将这组数据的每个数据比较,while结束的条件:end>=0;{printf("%d ", gap);if (arr[end] > tmp){arr[end + gap] = arr[end];//想继续和前面有序的数据比较,将end-gapend -= gap;}//到这里,arr[end]<tmp,那就不用赋值,直接将下标+gap,tmp的值随之改变,继续比较else {break;}}//在循环中,我们只是将大的数据往后赋值,那当初那个比较小的tmp赋给谁呢?//这组数据如何能比较结束(break)呢?肯定是此时的arr[end]并没有tmp大,不需要交换了//所以,我们把tmp值赋值给之前一个比较的值(由于是end-=gap,所以上一个是end+gap)arr[end + gap] = tmp;}}}
}
注意:为什么gap>1还可以对整段进行直插排序呢?
大家先想一想gap==1的条件:肯定是上一个gap>1因而进入了循环,进行了gap=gap/3+1,而gap/3=0,gap/3+1=1,接下来进行了直插。不会有其他意外。
n=10:
第一次,gap=n=10,大于1,进入循环之后,gap=gap/3+1=4,之后进行排序。
第二次,gap=4,大于1,进入循环,gap=gap/3+1=4/3+1=2,之后进行排序
注意gap=2的时候它仍然大于1 ,进入循环了,然后才进行的gap=gap/3+1,得到了gap=1,进行最后的直插
方法二(时间复杂度更优)
在上面的基础上进行优化:
之前是将一组一组比,现在仍然是相隔gap个的两个元素进行比较,但是当它俩比较完之后,我们不用找arr[0+gap]再隔gap的值。我们直接找arr[0]的下一个:arr[1],再找arr[1+gap],将他俩比较。那到什么时候停止呢?当i<n-gap时。

void ShellSort(int* arr, int n)
{int gap = n;while (gap>1){gap = gap / 3 + 1;for (int i=0; i < n - gap; i++){int end = i;int tmp = arr[end + gap];while (end >= 0) //将这组数据的每个数据比较,while结束的条件:end>=0;{if (arr[end] > tmp){arr[end + gap] = arr[end];//想继续和前面有序的数据比较,将end-gapend -= gap;}//到这里,arr[end]<tmp,那就不用赋值,直接将下标+gap,tmp的值随之改变,继续比较else {break;}}//在循环中,我们只是将大的数据往后赋值,那当初那个比较小的tmp赋给谁呢?//这组数据如何能比较结束(break)呢?肯定是此时的arr[end]并没有tmp大,不需要交换了//所以,我们把tmp值赋值给之前一个比较的值(由于是end-=gap,所以上一个是end+gap)arr[end + gap] = tmp;}}
}

希尔排序的时间复杂度是:O(n^1.3)

选择排序
堆排序
这是堆排序的文章,点击链接即可跳转
直接选择排序
这个名字中的“选择”已经暴露了它的方法,直接选择排序是从整个数组中(arr[0]到arr[n-1])选出来min或者max的元素,然后放在整个数组的第一个位置。然后再从arr[1]到arr[n-1]选出来min或max,放在第二个位置。【将min/max放在第一个位置,那原本的数据怎么办,所以不是直接将这个值放在第一个位置,而是将两个值交换】
-
思路:
-
- 先设定两个变量,begin和mini(它俩是下标),begin作为min或者max放置的位置的下标。mini作为遍历数组时此时位置的下标。[需要知道跳出循环的条件,即放的位置<n]

- 先设定两个变量,begin和mini(它俩是下标),begin作为min或者max放置的位置的下标。mini作为遍历数组时此时位置的下标。[需要知道跳出循环的条件,即放的位置<n]
-
但是又一个bug是:每找一次最大/最小值,就需要将数组遍历一遍(和冒泡排序一样费时间O(n^2)),时间复杂度很大,我们进行优化。
在遍历一遍数组的时候,我们可以将min和max同时找出来,将它们放在数组的两端。这样就可以省略一半的时间。【但需要注意的是,这个上面那个的循环结束条件就不一样了,我们不用再遍历后半部分,就是已经放好特定值的那部分】
void SelectSort(int* arr, int n)
{int begin=0;for (begin = 0; begin < n/2; begin++) //为什么begin<n/2呢?因为begin是前半部分的下标,只用占整个数组的一半{int maxi = begin;int mini = begin;//确定了这趟mini要放的位置,接下来这个循环用来遍历找最小值/最大值,用j来遍历int j = begin;for (j = begin+1; j < n-begin; j++) //为什么j<n-begin//第一遍遍历的时候,需要遍历所有的//第二次遍历,就不用遍历最后一个,已经放了特定的值//第三次遍历,倒数两个都不用遍历了{if (arr[j] < arr[mini])mini=j;if (arr[j] > arr[maxi])maxi=j;}//这一步是什么作用?if (maxi == begin){maxi = mini;}Swap(&arr[begin], &arr[mini]);Swap(&arr[n - 1 - begin], &arr[maxi]);}
}
其中这一步的作用是什么呢?
if (maxi == begin)
{maxi = mini;
}
举个例子:

这个的问题就在于:maxi刚好和begin重合了,而arr[begin]先一步和arr[mini]交换了,所以我们需要在交换之前处理一下:如果它俩重合了,那就先让maxi走到mini的位置。

if(maxi==begin)maxi=mini;
相关文章:

”插入排序“”选择排序“
文章目录 插入排序1. 直接插入排序(O(n^2))举例1:举例2:直插排序的"代码"直插排序的“时间复杂度” 2. 希尔排序(O(n^1.3))方法一方法二(时间复杂度更优) 选择排序堆排序直接选择排序 我们学过冒泡排序,堆排序等等。(回…...

烟花爆竹储存作业安全要求
烟花爆竹储存作业证是从事相关作业的法定凭证,旨在确保操作人员具备专业知识和安全技能,防止因违规操作引发火灾、爆炸等事故。根据《烟花爆竹安全管理条例》及相关法规,未取得作业证的人员不得从事烟花爆竹储存、搬运、管理等作业。 仓库选址…...

Python深度学习基础——卷积神经网络(CNN)(PyTorch)
CNN原理 从DNN到CNN 卷积层与汇聚 深度神经网络DNN中,相邻层的所有神经元之间都有连接,这叫全连接;卷积神经网络 CNN 中,新增了卷积层(Convolution)与汇聚(Pooling)。DNN 的全连接…...
Python判断语句全面解析:从基础到高级模式匹配)
Python(11)Python判断语句全面解析:从基础到高级模式匹配
目录 一、条件逻辑的工程价值1.1 真实项目中的逻辑判断1.2 判断语句类型矩阵 二、基础判断深度解析2.1 多条件联合判断2.2 类型安全判断 三、模式匹配进阶应用3.1 结构化数据匹配3.2 对象模式匹配 四、判断语句优化策略4.1 逻辑表达式优化4.2 性能对比测试 五、典型应用场景实战…...

MTK7628基于原厂的mtk-openwrt-sdk-20160324-8f8e4f1e.tar.bz2 源代码包,配置成单网口模式的方法
一、配置. 在SDK工程下,运行make kernel_menuconfig,如下图所示: Ralink Module --->选上“One Port Only”,如下图所示: 如果P0网口实现WAN口,就配置成W/LLLL,否则就配置成LLLL/W. 二、修改网口的原代…...

艾伦·图灵:计算机科学与人工智能之父
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 艾伦图灵:计算机科学与人工智能之父 一、天才的诞生与早期生涯 1912年6月…...

策略模式实现 Bean 注入时怎么知道具体注入的是哪个 Bean?
Autowire Resource 的区别 1.来源不同:其中 Autowire 是 Spring2.5 定义的注解,而 Resource 是 Java 定义的注解 2.依赖查找的顺序不同: 依赖注入的功能,是通过先在 Spring IoC 容器中查找对象,再将对象注入引入到当…...
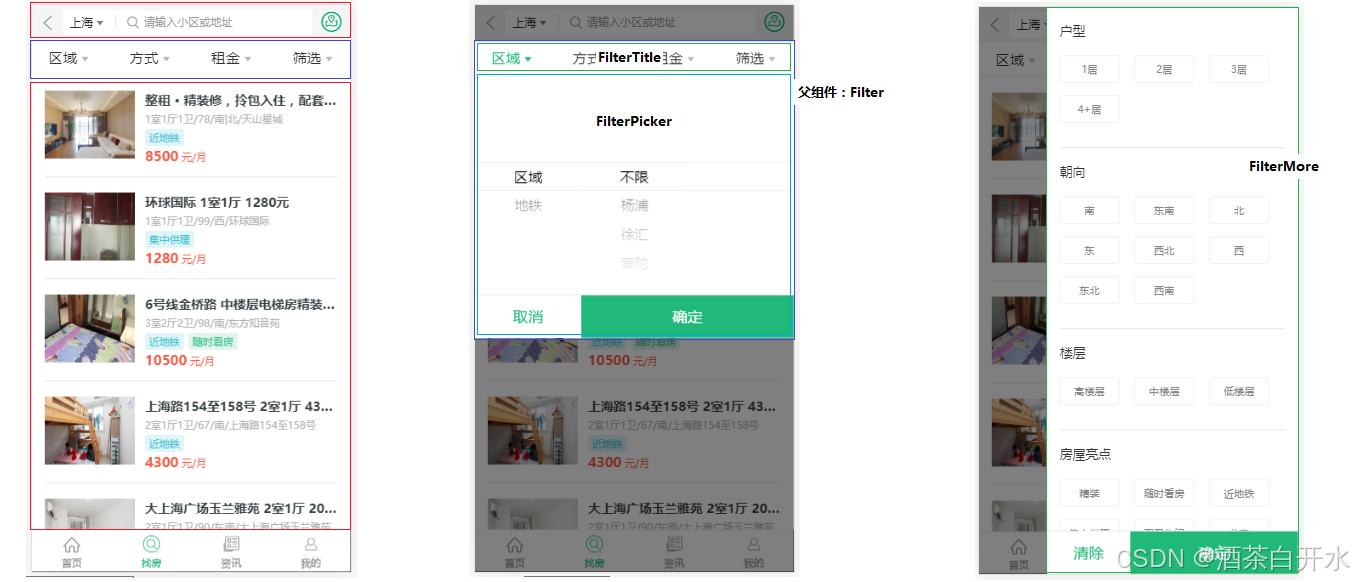
React九案例中
代码下载 地图找房模块 顶部导航栏 封装NavHeader组件实现城市选择,地图找房页面的复用,在 components 目录中创建组件 NavHeader,把之前城市列表写过的样式复制到 NavHeader.scss 下,在该组件中封装 antd-mobile 组件库中的 N…...

第一期:[特殊字符] 深入理解MyBatis[特殊字符]从JDBC到MyBatis——持久层开发的转折点[特殊字符]
前言 🌟 在软件开发的过程中,持久层(或数据访问层)是与数据库进行交互的关键部分。早期,开发者通常使用 JDBC(Java Database Connectivity)来实现与数据库的连接与操作。虽然 JDBC 在一定程度上…...

Adobe Photoshop 2025 Mac中文 Ps图像编辑
Adobe Photoshop 2025 Mac中文 Ps图像编辑 一、介绍 Adobe Photoshop 2025 Mac版集成了多种强大的图像编辑、处理和创作功能。①强化了Adobe Sensei AI的应用,通过智能抠图、自动修复、图像生成等功能,用户能够快速而精确地编辑图像。②3D编辑和动画功…...

用纯Qt实现GB28181协议/实时视频/云台控制/预置位/录像回放和下载/事件订阅/语音对讲
一、前言 在技术的长河中探索,有些目标一旦确立,便如同璀璨星辰,指引着我们不断前行。早在2014年,我心中就种下了用纯Qt实现GB28181协议的种子,如今回首,一晃十年已逝,好在整体框架和逻辑终于打…...

让你方便快捷实现主题色切换(useCssVar)
文章目录 前言一、useCssVar是什么?二、使用步骤1.安装依赖2.实现主题色切换 总结 前言 使用 CSS 变量(CSS Custom Properties)实现主题色切换是一种高效且易于维护的方法。通过将主题颜色定义为 CSS 变量,你可以轻松地在不同主题…...

面试之《websocket》
配置环境 mkdir express cd express npm init npm install express ws// index.js var app require("express")(); var WebSocket require("ws");var wss new WebSocket.Server({ port: 8888 });wss.on(connection, function connection(ws) {ws.on(m…...

Linux 内存调优之系统内存全面监控
写在前面 博文内容涉及 Linux 全局内存监控监控方式包括传统工具 vmstat/top/free/sar/slabtop ,以及 systemd-cgtop,proc 内存伪文件系统监控内容包括进程内存使用情况, 内存全局数据统计,内存事件指标,以及进程内存段数据监控理解不足小伙伴帮忙指正 😃,生活加油我看远…...
:cat)
每天学一个 Linux 命令(14):cat
Linux 文件查看与合并命令:cat cat(全称 concatenate)是 Linux 中用于查看文件内容、合并文件或创建简单文件的基础命令。它操作简单但功能灵活,是日常文件处理的常用工具。 1. 命令作用 查看文件内容:直接输出文件内容到终端。合并文件:将多个文件内容合并输出或保存到…...

L36.【LeetCode题解】查找总价格为目标值的两个商品(剑指offer:和为s的两个数字) (双指针思想,内含详细的优化过程)
目录 1.LeetCode题目 2.分析 方法1:暴力枚举(未优化的双指针) 方法2:双指针优化:利用有序数组的单调性 版本1代码 提问:版本1代码有可以优化的空间吗? 版本2代码 提问:版本2代码有可以优化的空间吗? 版本3代码(★推荐★) 3.牛客网题目:和为s的数字 1.LeetCode题目 …...

英语学习4.9
cordial 形容词: 热情友好的,诚恳的 表示一个人态度温和、亲切,给人温暖和善的感觉。 令人愉快的,和睦的 形容关系融洽、氛围和谐。 例句: The two leaders had a cordial but formal discussion. &am…...

HBuilderX 开发的uniapp项目在微信开发者工具中调试运行
HBuilderX 开发的uniapp项目在微信开发者工具中调试运行 或者运行失败 https://blog.csdn.net/m0_74141658/article/details/129541365?fromshareblogdetail&sharetypeblogdetail&sharerId129541365&sharereferPC&sharesourceweixin_48616345&sharefromf…...

【特权FPGA】之乘法器
完整代码如下: timescale 1ns / 1ps// Company: // Engineer: // // Create Date: 23:08:36 04/21/08 // Design Name: // Module Name: mux_16bit // Project Name: // Target Device: // Tool versions: // Description: // // Dependencies: …...

MyBatis-Plus 核心功能
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 一、条件构造器1、核心 Wrapper 类型基础查询示例SQL 查询使用 QueryWrapper 实现查询 更新操作示例场景一:基础更新SQL 查询使用 QueryWrapper 实现更新…...

前端工程化-包管理NPM-package.json 和 package-lock.json 详解
package.json 和 package-lock.json 详解 1.package.json 基本概念 package.json 是 Node.js 项目的核心配置文件,它定义了项目的基本信息、依赖项、脚本命令等。 主要字段 基本信息字段 name: 项目名称(必填) version: 项目版本…...

Day22 -php开发01--留言板+知识点(超全局变量 文件包含 数据库操作 第三方插件)
环境要求:php7.0.9 小皮 navicat phpstorm24.1 知识点:会写(留言板 留言板后台) 超全局变量 三方插件的使用 文件包含 1、开启小皮并利用navicat新建一个数据库 注意:本地的服务mysql关闭后 才可打开小皮。属…...

Java工具类-assert断言
我们可能经常在项目的单元测试或者一些源码中看到别人在使用assert关键字,当然也不只是Java语言,很多编程语言也都能看到,我们大概知道断言可以用于测试中条件的校验,但却不经常使用,本文总结了Java中该工具类的使用。…...

A2A协议分析报告
A2A协议分析报告 一、引言 在人工智能快速发展的背景下,智能体(Agent)技术逐步成为企业数字化转型的关键支撑。为了打破不同智能体之间协作壁垒,提升多模态协同效率,Google 于2025年推出了“Agent-to-Agentÿ…...

人工智能、机器学习与深度学习-AI基础Day2
核心概念与技术全景解析 近年来,人工智能(AI)技术飞速发展,逐渐渗透到生活的方方面面。然而,对于许多人来说,AI、机器学习(ML)、深度学习(DL)以及生成式人工…...

GGML源码逐行调试(上)
目录 前言1. 简述2. 环境配置3. ggml核心概念3.1 gguf3.2 ggml_tensor3.3 ggml_backend_buffer3.4 ggml_context3.5 backend3.6 ggml_cgraph3.7 ggml_gallocr 4. 推理流程整体梳理4.1 时间初始化与参数设置4.2 模型加载与词汇表构建4.3 计算图与内存分配4.4 文本预处理与推理过…...

SpringCloud-OpenFeign
前言 1.存在问题 远程调用可以像Autowired一样吗 服务之间的通信⽅式,通常有两种:RPC和HTTP. 在SpringCloud中,默认是使⽤HTTP来进⾏微服务的通信,最常⽤的实现形式有两种: RestTemplate OpenFeign RPC(RemoteProcedureCall)远程过程调⽤&…...
撰写学位论文Word图表目录的自动生成
第一步:为图片和表格添加题注 选中图片或表格 右键点击需要编号的图片或表格,选择 【插入题注】(或通过菜单栏 引用 → 插入题注)。 设置题注标签 在弹窗中选择 标签(如默认有“图”“表”,若无需自定义标…...

Web 项目实战:构建属于自己的博客系统
目录 项目效果演示 代码 Gitee 地址 1. 准备工作 1.1 建表 1.2 引入 MyBatis-plus 依赖 1.3 配置数据库连接 1.4 项目架构 2. 实体类准备 - pojo 包 2.1 dataobject 包 2.2 request 包 2.3 response 包 2.3.1 统一响应结果类 - Result 2.3.2 用户登录响应类 2.3.3…...

分库分表设计与Java实践:从理论到实现
在分布式系统和高并发场景下,单一数据库的性能瓶颈逐渐显现,分库分表成为提升数据库扩展性和性能的重要手段。作为Java开发者,掌握分库分表的设计原则和实现方法,不仅能应对海量数据和高并发的挑战,还能优化系统架构的…...
