力扣每日打卡 1922. 统计好数字的数目 (中等)
力扣 1922. 统计好数字的数目 中等
- 前言
- 一、题目内容
- 二、解题方法
- 1. 暴力解法(会超时,此法不通)
- 2. 快速幂运算
- 3. 组合计数的思维
- 逻辑分析
- 组合计数的推导
- 例子分析
- 思维小结论
- 4.官方题解
- 4.1 方法一:快速幂
- 三、快速幂运算
- 快速幂运算(Exponentiation by Squaring)
- 基本思想
- 算法实现(②③为非递归)
- ① 递归运算
- ② 普通 除模运算(不带 **模数** 与 带 **模数**)
- ③ 按位与运算
- 使用示例
- 示例代码
- 复杂度分析
- 小结论
- 四、JS的大数运算
- 1. 数字精度限制
- 2. 大数解决方案
- 2.1. 使用 BigInt
- 2.2. 使用第三方库
- 2.3. 总结
- 2.4 补充:本题使用大数运算的例子
前言
这是刷算法题的第十一天,用到的语言是JS
题目:力扣 1922. 统计好数字的数目 (中等)
一、题目内容
我们称一个数字字符串是 好数字 当它满足(下标从 0 开始)偶数 下标处的数字为 偶数 且 奇数 下标处的数字为 质数 (2,3,5 或 7)。
比方说,“2582” 是好数字,因为偶数下标处的数字(2 和 8)是偶数且奇数下标处的数字(5 和 2)为质数。但 “3245” 不是 好数字,因为 3 在偶数下标处但不是偶数。
给你一个整数 n ,请你返回长度为 n 且为好数字的数字字符串 总数 。由于答案可能会很大,请你将它对 109 + 7 取余后返回 。
一个 数字字符串 是每一位都由 0 到 9 组成的字符串,且可能包含前导 0 。
示例 1:
输入:n = 1
输出:5
解释:长度为 1 的好数字包括 “0”,“2”,“4”,“6”,“8” 。
示例 2:
输入:n = 4
输出:400
示例 3:
输入:n = 50
输出:564908303
提示:
1 <= n <= 1015
二、解题方法
1. 暴力解法(会超时,此法不通)
- 遍历所有长度为n的数字字符串,判断是否为好数字
- 好数字的偶数下标处的数字为偶数且奇数下标处的数字为质数
- 时间复杂度为O(n),空间复杂度为O(1)
- 由于n的范围较大,暴力解法会超时,所以需要优化
代码如下(实例):
*** @param {number} n* @return {number}*/
var countGoodNumbers = function (n) {// 暴力解法let count = 0for(let i = 0; i.toString().length <= n; i++) {if (i.toString().length === n) {const si = i.toString() // 将数字转换为字符串if (si.length > n) returnfor (let j = 0; j < si.length; j++) {let access = false // 如果每一位数字都通过,则数量+1if (j % 2 === 0 && si[j] % 2 === 0) access = trueelse breakif( j > 10 ) {if (j % 2 && (si[j] % 2 === 2 || si[j] % 2 === 3 || si[j] % 2 === 5 || si[j] % 2 === 7)) access = trueelse break}if (access) count++}}}return count % (10 ** 9 + 7)
}// console.log(countGoodNumbers(1)) // 5 正确,也会打印,但也仅此而已
// console.log(countGoodNumbers(8)) // 40000000 正确,也会打印,但也仅此而已
// console.log(countGoodNumbers(9)) // 400000000正确,但是不会打印,可能直接超时了,或者打印时间非常慢
2. 快速幂运算
涉及到JS的 大数运算(关于大数运算的补充在下面有)
代码如下(示例):(使用了JS的 大数运算 )
/*** @param {number} n* @return {number}*/
var countGoodNumbers = function (n) {// 此题无法使用暴力算法const MOD = BigInt(10 ** 9 + 7)// ai得到的逻辑思维:// 一个长度为n的字符串,偶数位置可以有02468五种选择,奇数位置可以有2357四种选择// 因此对其进行排列组合,可以得到好数字的个数一共是 (符合偶数位置的数字的个数 * 符合奇数位置的数字的个数)// 即 (5^evenFuhe) * (4^oddFuhe)const evenCount = BigInt(Math.ceil(n / 2)) // 偶数下标的数量const oddCount = BigInt(Math.floor(n / 2)) // 奇数下标的数量const count = (Fuhe(5n, evenCount, MOD) * Fuhe(4n, oddCount, MOD)) % MODreturn Number(count)
}// 快速幂运算的函数实现
const Fuhe = ( a, b, mod ) => {let ans = 1na = a % modwhile(b) {if( b & 1n) ans = (a * ans) % moda = (a * a) % modb >>= 1n}return ans
}
代码:(下面的代码没有使用JS的 大数运算,会出现精准度问题)
/*** @param {number} n* @return {number}*/
var countGoodNumbers2 = function (n) {// 此题无法使用暴力算法const MOD = 10 ** 9 + 7// ai得到的逻辑思维:// 一个长度为n的字符串,偶数位置可以有02468五种选择,奇数位置可以有2357四种选择// 因此对其进行排列组合,可以得到好数字的个数一共是 (符合偶数位置的数字的个数 * 符合奇数位置的数字的个数)// 即 (5^evenFuhe) * (4^oddFuhe)const evenCount = Math.ceil(n / 2) // 偶数下标的数量const oddCount = Math.floor(n / 2) // 奇数下标的数量const count = (Fuhe(5, evenCount, MOD) * Fuhe(4, oddCount, MOD)) % MODreturn count
}
const Fuhe = ( a, b, mod ) => {let ans = 1a = a % modwhile(b) {if( b & 1) ans = (a * ans) % moda = (a * a) % modb >>= 1// b = Math.floor(b / 2) }return ans
}
console.log(countGoodNumbers2(50)) // 应该是564908303,而非564908313,但是打印的是564908313
3. 组合计数的思维
理解这个问题的数学思维需要我们从组合计数的角度出发,分析如何在特定的约束下选择数字字符串。以下是分析的详解:
逻辑分析
-
字符串结构:
- 我们需要生成的字符串长度为 ( n )。
- 字符串的下标为 ( 0 ) 到 ( n-1 )。
-
下标分类:
- 偶数下标(如 0, 2, 4, …)和奇数下标(如 1, 3, 5, …)之间有不同的限制条件。
- 偶数下标位置的数字必须是偶数。
- 奇数下标位置的数字必须是质数。
-
可能的选项:
- 偶数的选择: 偶数下标的位置可以选择的数字有 0, 2, 4, 6, 8,共 5 种选择。
- 质数的选择: 奇数下标的位置可以选择的质数有 2, 3, 5, 7,共 4 种选择。
组合计数的推导
-
偶数下标的数量:
- 在一个长度为 ( n ) 的字符串中,偶数下标的数量可以通过 evenCount = ⌈n / 2⌉计算得出。
- 这表示当 ( n ) 为奇数时,偶数下标数量会比奇数下标数量多 1。
- 在一个长度为 ( n ) 的字符串中,偶数下标的数量可以通过 evenCount = ⌈n / 2⌉计算得出。
-
奇数下标的数量:
- 奇数下标的数量可以通过 oddCount = ⌊ n / 2 ⌋计算得出。
- 这表示当 ( n ) 为偶数时,偶数下标和奇数下标数量相等。
- 奇数下标的数量可以通过 oddCount = ⌊ n / 2 ⌋计算得出。
-
总组合数的计算:
- 对于每一个偶数下标,我们有 5 种选择(偶数)。
- 对于每一个奇数下标,我们有 4 种选择(质数)。
- 最终的好数字字符串数量可以通过将偶数下标的选择和奇数下标的选择相乘得到:
goodNumbers = 5evenCount × 4oddCount
例子分析
假设 ( n = 4 ):
- 字符串有长度 4,下标为 0, 1, 2, 3。
- 偶数下标(0 和 2): 2 个位置,每个位置可以选择【0, 2, 4, 6, 8】中的任意一个,即 5 种选择。
- 奇数下标(1 和 3): 2 个位置,每个位置可以选择【2, 3, 5, 7】中的任意一个,即 4 种选择。
因此,字符串的组合数是:
goodNumbers = 52 × 42 = 25 × 16 = 400
思维小结论
通过这样的数学推理,我们能够清楚地理解在给定的条件下,为什么能够将问题转换为计算选项的排列组合。在面对其他类似的问题时,这种分解和组合的思维方式可以帮助我们有效解决复杂问题。
4.官方题解
4.1 方法一:快速幂
思路与算法:
对于偶数下标处的数字,它可以为 0,2,4,6,8 共计 5 种,而长度为 n 的数字字符串有 ⌊ n+1 / 2 ⌋ 个偶数下标,其中 ⌊x⌋ 表示对 x 向下取整。
对于奇数下标处的数字,它可以为 2,3,5,7 共计 4 种,而长度为 n 的数字字符串有 ⌊ n / 2 ⌋ 个奇数下标。
因此长度为 n 的数字字符串中,好数字的总数即为:
5^⌊ n+1 / 2 ⌋^ ⋅ 4^⌊ n / 2 ⌋^
在本题中,由于 n 的取值最大可以到 1015,如果通过普通的乘法运算直接求出上式中的幂,会超出时间限制,因此我们需要使用快速幂算法对幂的求值进行优化。
快速幂算法可以参考「50. Pow(x, n)」的官方题解。
代码如下(示例):
var countGoodNumbers = function(n) {const mod = 1000000007n;// 快速幂求出 x^y % modfunction quickmul(x, y) {let ret = 1n;let mul = x;while (y > 0) {if (y % 2n === 1n) {ret = (ret * mul) % mod;}mul = (mul * mul) % mod;y = y / 2n;}return ret;}return Number(quickmul(5n, BigInt(n + 1) / 2n) * quickmul(4n, BigInt(n) / 2n) % mod);
};作者:力扣官方题解
链接:https://leetcode.cn/problems/count-good-numbers/solutions/857968/tong-ji-hao-shu-zi-de-shu-mu-by-leetcode-53jj/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
- 复杂度分析:
- 时间复杂度:O(log n)。
- 空间复杂度:O(1)。
链接:力扣本题官方题解
来源:力扣(LeetCode)
三、快速幂运算
快速幂运算(Exponentiation by Squaring)
快速幂运算是一种高效计算 ( b^e ) 的算法,其中 ( b ) 是基数,( e ) 是指数。传统的逐步乘法方法的时间复杂度为 ( O(e) ),而快速幂运算的时间复杂度为 ( O(\log e) ),因此在处理大数时特别有效。
基本思想
快速幂运算的基本思想是利用平方和乘法来减少乘法的次数。其主要依据是:
- 如果指数 ( e ) 为偶数,则 ( b^e = (b{e/2})2 )
- 如果指数 ( e ) 为奇数,则 ( b^e = b \times b^{e-1} )
通过这种方式,可以在每次迭代中将指数减半,从而显著降低计算时间。
算法实现(②③为非递归)
以下是使用 JavaScript 实现的快速幂运算的代码:
① 递归运算
/** 不带模数* 快速幂运算* @param {number} base - 基数* @param {number} exp - 指数* @returns {number} */
function quickPow(base, exp) {if (exp === 0) {return 1; // 任何数的零次方为 1}if (exp % 2 === 0) {const half = quickPow(base, exp / 2);return half * half;} else {return base * quickPow(base, exp - 1);}
}
② 普通 除模运算(不带 模数 与 带 模数)
/** 不带模数* 快速幂运算* @param {number} a- 基数* @param {number} b- 指数* @returns {number} 计算结果 (a ^ b)*/
function quick (a, b) {let ans = 1while(b) { // 当指数存在的时候// 如果指数是奇数,则要先拉出来一个底数乘到最终结果上,其余步骤和偶数一样操作// 如果指数是偶数,则要底数平方,指数除以2(如果是使用按位与运算,则使用 "b >>= 1")b/2if(b % 2 === 1) ans *= aa *= ab = Math.floor(b / 2) // 注意一定要使用Math.floor(),否则会出现小数点,导致结束循环}return ans
}
console.log(quick(2, 7)) // 128/** 带模数* 快速幂运算* @param {number} base - 基数* @param {number} exp - 指数* @param {number} mod - 模数* @returns {number} 计算结果 (base^exp) % mod*/
const modExp = (base, exp, mod) => {let result = 1; // 初始化结果为 1base = base % mod; // 将基数在模数下取值while (exp > 0) {// 如果 exp 为奇数,将当前的 base 乘入结果if (exp % 2 === 1) result = (result * base) % mod;// 将 base 平方base = (base * base) % mod;// exp 右移,相当于整除 2exp = Math.floor(exp / 2);}return result; // 返回最终结果
}
③ 按位与运算
/** 不带模数* 快速幂运算* @param {number} a- 基数* @param {number} b- 指数* @returns {number} 计算结果 (a ^ b)*
function quick2 (a, b) {let ans = 1while(b) { // 当指数存在的时候// 如果指数是奇数,则要先拉出来一个底数乘到最终结果上,其余步骤和偶数一样操作// 如果指数是偶数,则要底数平方,指数除以2(如果是使用按位与运算,则使用 "b >>= 1")b/2if(b & 1) ans *= aa *= ab >>= 1 // b右移一位}return ans
}
console.log(quick2(2, 8)) // 256
使用示例
快速幂运算可以用于很多应用场景,包括计算大数的幂、加密算法、以及任何需要快速计算大数时。
示例代码
const MOD = 10 ** 9 + 7; // 定义模数console.log(modExp(2, 10, MOD)); // 输出: 1024
console.log(modExp(5, 3, MOD)); // 输出: 125
console.log(modExp(3, 7, MOD)); // 输出: 2187
console.log(modExp(10, 9, MOD)); // 输出: 1000000000
复杂度分析
- 时间复杂度: ( O(log e) ) — 每次操作将指数减半。
- 空间复杂度: ( O(1) ) — 仅使用常量级额外空间。
小结论
快速幂运算是一个非常实用且高效的算法,广泛应用于计算大数的幂以及各种算法中。了解并实现该算法可以显著提高程序运行效率,特别是在处理与模数运算相关的问题时。
四、JS的大数运算
JavaScript 在处理数字时,其默认的数值类型是基于 IEEE 754 标准的双精度浮点数。这个数值类型有一些限制,特别是在进行大数运算时。以下是 JavaScript 中大数运算的简单介绍:
1. 数字精度限制
-
安全整数: JavaScript 支持的安全整数范围是 (-2^{53} + 1) 到 (2^{53} - 1)(即
Number.MAX_SAFE_INTEGER的值为 9007199254740991)。超出这个范围的整数计算可能会出现精度丢失(例如,9007199254740992会变成9007199254740992)。 -
浮点数问题: 由于浮点数的表示方式,某些小数(如
0.1和0.2的和)可能无法精确表示。
2. 大数解决方案
由于上述限制,处理大数运算时,可以考虑以下几种方案:
2.1. 使用 BigInt
从 ES2020 开始,JavaScript 引入了 BigInt 类型,用于表示任意大小的整数。你可以通过在数字后添加 “n” 来创建 BigInt:
const bigInt1 = BigInt(9007199254740992)
const bigInt2 = 12345678901234567890n // 后缀 "n" 表示 BigInt
const sum = bigInt1 + bigInt2 // 可以进行大数运算
console.log(sum) // 输出: 12345678901234567892nconsole.log(Number(sum)) // 输出: 12345678901234567892
2.2. 使用第三方库
如果你需要支持比 BigInt 更广泛的数值(比如更复杂的数学操作、浮点数等),可以使用大数运算库,例如:
- Decimal.js: 支持任意精度的十进制运算,适合处理小数。
- Big.js: 提供了对大浮点数的高精度运算支持。
- bignumber.js: 可以处理比较大的数值以及高精度的浮点数运算。
使用示例(以 decimal.js 为例):
const Decimal = require('decimal.js');const a = new Decimal(0.1);
const b = new Decimal(0.2);
const sum = a.plus(b); // 精确计算
console.log(sum.toString()); // 输出: "0.3"
2.3. 总结
在 JavaScript 中,大数运算可以通过 BigInt 来实现任意大小的整数计算,或使用第三方库来处理更复杂的场景(如浮点数和高精度计算)。在处理大数运算时,需要注意原生数值类型的限制,以确保计算的准确性。
2.4 补充:本题使用大数运算的例子
代码如下:
/*** @param {number} n* @return {number}*/
var countGoodNumbers = function (n) {// 此题无法使用暴力算法const MOD = BigInt(10 ** 9 + 7)// ai得到的逻辑思维:// 一个长度为n的字符串,偶数位置可以有02468五种选择,奇数位置可以有2357四种选择// 因此对其进行排列组合,可以得到好数字的个数一共是 (符合偶数位置的数字的个数 * 符合奇数位置的数字的个数)// 即 (5^evenFuhe) * (4^oddFuhe)const evenCount = BigInt(Math.ceil(n / 2)) // 偶数下标的数量const oddCount = BigInt(Math.floor(n / 2)) // 奇数下标的数量const count = (Fuhe(5n, evenCount, MOD) * Fuhe(4n, oddCount, MOD)) % MODreturn Number(count)
}// 快速幂运算的函数实现
const Fuhe = ( a, b, mod ) => {let ans = 1na = a % modwhile(b) {if( b & 1n) ans = (a * ans) % moda = (a * a) % modb >>= 1n}return ans
}
相关文章:
)
力扣每日打卡 1922. 统计好数字的数目 (中等)
力扣 1922. 统计好数字的数目 中等 前言一、题目内容二、解题方法1. 暴力解法(会超时,此法不通)2. 快速幂运算3. 组合计数的思维逻辑分析组合计数的推导例子分析思维小结论 4.官方题解4.1 方法一:快速幂 三、快速幂运算快速幂运算…...

上层 Makefile 控制下层 Makefile 的方法
在复杂的项目中,通常会将项目划分为多个模块或子项目,每个模块都有自己的 Makefile。上层 Makefile 的作用是协调和控制这些下层 Makefile 的构建过程。下面是几种常见的示例,实现上层 Makefile 对下层 Makefile 的控制。 直接调用࿱…...
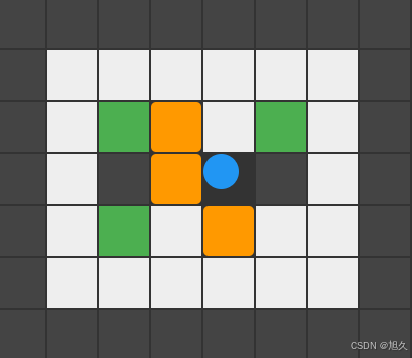
html简易实现推箱子小游戏原理(易上手)
实现效果 使用方向键移动,将橙色箱子推到绿色目标区域(黑色块为墙,白色块为可通过区域,蓝球为小人) 实现过程 <!DOCTYPE html> <html> <head><title>推箱子小游戏</title><style&g…...

搭建一个Spring Boot聚合项目
1. 创建父项目 打开IntelliJ IDEA,选择 New Project。 在创建向导中选择 Maven,确保选中 Create from archetype,选择 org.apache.maven.archetypes:maven-archetype-quickstart。 填写项目信息: GroupId:com.exampl…...

字符串与栈和队列-算法小结
字符串 双指针 反转字符串(双指针) 力扣题目链接 void reverseString(vector<char>& s) {for (int i 0, j s.size() - 1; i < s.size()/2; i, j--) {swap(s[i],s[j]);} }反转字符串II 力扣题目链接 遍历字符串的过程中,只要让 i (2 * k)&#…...

类似东郊到家的上门按摩预约服务系统小程序APP源码全开源
🔥 为什么上门按摩正在席卷全国? 万亿蓝海市场爆发 2024年中国按摩市场规模突破8000亿,上门服务增速达65% 90后成消费主力,**72%**白领每月至少使用1次上门按摩(数据来源:艾媒咨询) 传统痛点…...

Python | 在Pandas中按照中值对箱形图排序
箱形图是可视化数据分布的强大工具,因为它们提供了对数据集内的散布、四分位数和离群值的洞察。然而,当处理多个组或类别时,通过特定的测量(如中位数)对箱形图进行排序可以提高清晰度并有助于揭示模式。在本文中&#…...
)
[实战] 二分查找与哈希表查找:原理、对比与C语言实现(附完整C代码)
二分查找与哈希表查找:原理、对比与C语言实现 一、引言 在计算机科学中,高效的数据查找是核心问题之一。本文深入解析两种经典查找算法:二分查找与哈希表查找,从算法原理、时间复杂度、适用场景到完整C语言实现,提供…...

游戏引擎学习第215天
总结并为今天做铺垫 今天的工作内容是解决调试系统中的一个小问题。昨天我们已经完成了大部分的调试系统工作,但还有一个小部分没有完全处理,那就是关于如何层次化组织数据的问题。我们遇到的一个问题是,演示代码中仍有一个尚未解决的部分&a…...

【Redis】redis事物与管道
Redis 事务(Transaction) 事务概念 事务:是一组操作的集合,是不可分割的工作单元。Redis 事务特点: 一个事务可以一次执行多个命令。所有命令都被顺序化,形成一个队列。所有命令在执行 EXEC 时一次性、顺…...

Django信号使用完全指南示例
推荐超级课程: 本地离线DeepSeek AI方案部署实战教程【完全版】Docker快速入门到精通Kubernetes入门到大师通关课AWS云服务快速入门实战目录 **引言:****先决条件:****目录:****1. 什么是Django信号?****2:设置你的Django项目****2.1. 安装Django**2.2. 创建一个Django项…...
的计算)
DeepSeek BLEU和ROUGE(Recall)的计算
以下是 BLEU Score (Bilingual Evaluation Understudy)和 ROUGE Score(Recall-Oriented Understudy for Gisting Evaluation) 的原生Python实现(不依赖第三方库),通过分步计算逻辑和示例详细说明。 一、BLEU Score 实现 核心逻辑…...

vulkanscenegraph显示倾斜模型(5.9)-vsg中vulkan资源的编译
前言 上一章深入剖析了GPU资源内存及其管理,vsg中为了提高设备内存的利用率,同时减少内存(GPU)碎片,采用GPU资源内存池机制(vsg::MemoryBufferPools)管理逻辑缓存(VkBuffer)与物理内存(VkDeviceMemory)。本章将深入vsg中vulkan资源的编译(包含…...

今日行情明日机会——20250409
今日行情还需要考虑关税对抗~ 2025年4月8日涨停的主要行业方向分析 1. 军工(19家涨停) 细分领域:国防装备、航空航天、军民融合。催化因素:国家安全战略升级、国防预算增加、重大军工项目落地预期。 2. 免税(15家涨…...

XHR、FetchAxios详解网络相关大片文件上传下载
以下是 XHR(XMLHttpRequest) 与 Fetch API 的全面对比分析,涵盖语法、功能、兼容性等核心差异: 一、语法与代码风格 XHR(基于事件驱动) 需要手动管理请求状态(如 onreadystatechange 事件)和错误处理,代码冗长且易出现回调地狱。 const xhr = new XMLHttpRequest(); x…...
之元组)
Python基础总结(四)之元组
文章目录 一、元组格式二、元组操作2.1 转换元组 与 列表一样,元组也是序列,唯一的区别在于元组是不能修改的,与字符串一样。 一、元组格式 元组的创建方式很简单,秩序用逗号将元素隔开就能自动创建一个元组 示例: …...

系统分析师(六)-- 计算机网络
概述 TCP/IP 协议族 DNS DHCP 网络规划与设计 逻辑网络设计 物理网络设计 题目 层次化网络设计 网络冗余设计 综合布线系统 IP地址 网络接入技术 其他网络技术应用 物联网...

【前端】【React】useCallback的作用与使用场景总结
一、useCallback 的作用与使用场景总结 useCallback 是 React 提供的一个 Hook,用于缓存函数的引用,避免因为组件重新渲染而导致函数地址发生变化。它返回一个记忆(memoized)后的回调函数,只有当依赖项发生变化时才会…...

Qwen2.5-VL Technical Report 论文翻译和理解
一、TL;DR Qwen2.5-VL是QwenVL的最新模型,在视觉识别、精准目标定位、稳健文档解析以及长视频理解等方面实现了重大突破引入了动态分辨率处理和绝对时间编码,使其能够处理不同尺寸的图像以及长达数小时的视频,并实现秒级事件定位…...

Foxmail邮件客户端跨站脚本攻击漏洞(CNVD-2025-06036)技术分析
Foxmail邮件客户端跨站脚本攻击漏洞(CNVD-2025-06036)技术分析 漏洞背景 漏洞编号:CNVD-2025-06036 CVE编号:待分配 厂商:腾讯Foxmail 影响版本:Foxmail < 7.2.25 漏洞类型&#x…...

C语言打印的坑
使用下面的代码buf dprt("data: 0x%02x 0x%02x 0x%02x 0x%02x 0x%02x 0x%02x", buf[0], buf[1], buf[2], buf[3], buf[4], buf[5]); 明明是一个字节一个字节的打,打出来的数据有些却是4个字节 0xffffffff 0xffffffff 0xffffffff 0x7f 0xffffffff 0x7f0…...

高并发内存池(三):PageCache(页缓存)的实现
前言: 在前两期内容中,我们深入探讨了内存管理机制中在 ThreadCache 和 CentralCache两个层级进行内存申请的具体实现。这两层缓存作为高效的内存分配策略,能够快速响应线程的内存需求,减少锁竞争,提升程序性能。 本期…...

pycharm已有python3.7,如何新增Run Configurations中的Python interpreter为python 3.9
在 PyCharm 中,如果你已经安装了 Python 3.9,并且希望在 Run Configurations 中新增一个 Python 3.9 的解释器,可以按照以下步骤操作: 步骤 1:打开 PyCharm 设置 点击 PyCharm 左上角的 File 菜单。选择 Settings&am…...

Linux驱动开发-网络设备驱动
Linux驱动开发-网络设备驱动 一,网络设备总体结构1.1 总体架构1.2 NAPI数据处理机制 二,RMII和MDIO2.1 RMII接口2.2 MDIO接口 三,MAC和PHY模块3.1 MAC模块3.2 PHY模块 四,网络模型4.1 网络的OSI和TCP/IP分层模型4.1.1 传输层&…...

学习笔记083——Java Stream API
文章目录 1、过滤数据 filter()2、转换元素 map()3、排序 sorted()3.1、自定义排序规则 4、去重 distinct()5、限制元素数量 limit()6、收集结果 collect()6.1、收集为List6.2、收集为Set6.3、转为Map6.4、基本用法(注意键冲突会抛异常)6.5、处理键冲突&…...

DataEase同比环比
DataEase同比环比 前言术语实现表结构设计DataEase设计创建数据集创建仪表盘最后前言 某大数据项目,需要比较展示今年跟去年的数据,如下图: 说明:比较24,25的产品销量,相同月份做一组,并排放一块 还有更进一步: 说明:比较24,25相同月份,相同产品的销量 直接用DataE…...

RAG 工程基础
RAG 概念 RAG(Retrieval - Augmented Generation)技术是一种将检索与生成相结合的人工智能技术,旨在利用外部知识源来增强语言模型的生成能力,提高生成内容的质量、准确性和相关性。 具体来说,RAG 技术在处理用户输入的…...

基础算法:滑动窗口_python版本
能使用滑动窗口的题,基本都需要数字为正整数,这样才能保证滑入一个数字总和是增加的(单调性) 一、209. 长度最小的子数组 思路: 已每个位置为右端点,依次加大左端点,最短不满足 sum(num[left,right]) < target的。…...

Qt 之opengl shader language
着色器示例代码 实际运行效果...

PyRoboPlan 库,给 panda 机械臂微分 IK 上大分,关节限位、碰撞全不怕
视频讲解: PyRoboPlan 库,给 panda 机械臂微分 IK 上大分,关节限位、碰撞全不怕 代码仓库:https://github.com/LitchiCheng/mujoco-learning 今天分享PyRoboPlan库,比之前的方式优点在于,这个库考虑了机械…...
