算法思想之前缀和(二)
欢迎拜访:雾里看山-CSDN博客
本篇主题:算法思想之前缀和(二)
发布时间:2025.4.11
隶属专栏:算法

目录
- 算法介绍
- 核心思想
- 大致步骤
- 例题
- 和为 K 的子数组
- 题目链接
- 题目描述
- 算法思路
- 代码实现
- 和可被 K 整除的子数组
- 题目链接
- 题目描述
- 算法思路
- 代码实现
- 连续数组
- 题目链接
- 题目描述
- 算法思路
- 代码实现
- 矩阵区域和
- 题目链接
- 题目描述
- 算法思路
- 代码实现
算法介绍
核心思想
前缀和(Prefix Sum) 是一种预处理数组的方法,通过预先计算并存储数组的累积和,将区间和查询的时间复杂度从 O(n) 优化至 O(1),适用于频繁查询子数组和的场景。
大致步骤
- 预处理出来一个前缀和数组
- 使用前缀和数组
- 处理边界情况
例题
和为 K 的子数组
题目链接
560. 和为 K 的子数组
题目描述
给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。
子数组是数组中元素的连续非空序列。
示例 1:输入:nums = [1,1,1], k = 2
输出:2示例 2:
输入:nums = [1,2,3], k = 3
输出:2提示:
1 <= nums.length <= 2 * 104-1000 <= nums[i] <= 1000-107 <= k <= 107
算法思路
设 i 为数组中的任意位置,用 sum[i] 表示 [0, i] 区间内所有元素的和。
想知道有多少个以 i 为结尾的和为 k 的子数组,就要找到有多少个起始位置为 x1, x2, x3... 使得 [x, i] 区间内的所有元素的和为 k 。那么 [0, x] 区间内的和是不是就是sum[i] - k 了。于是问题就变成:
- 找到在
[0, i - 1]区间内,有多少前缀和等于sum[i] - k的即可。
我们不用真的初始化一个前缀和数组,因为我们只关心在 i 位置之前,有多少个前缀和等于sum[i] - k 。因此,我们仅需用一个哈希表,一边求当前位置的前缀和,一边存下之前每一种前缀和出现的次数。
代码实现
class Solution {
public:int subarraySum(vector<int>& nums, int k) {unordered_map<int, int> hash;hash[0] = 1;int n = nums.size(), sum = 0, ret = 0;for(int i = 0; i < n; i++){sum += nums[i];if(hash[sum-k] > 0)ret += hash[sum-k];hash[sum]++;}return ret;}
};

和可被 K 整除的子数组
题目链接
974. 和可被 K 整除的子数组
题目描述
给定一个整数数组
nums和一个整数k,返回其中元素之和可被k整除的非空 子数组 的数目。
子数组 是数组中 连续 的部分。
示例 1:输入:nums = [4,5,0,-2,-3,1], k = 5
输出:7
解释:
有 7 个子数组满足其元素之和可被 k = 5 整除:
[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]示例 2:
输入: nums = [5], k = 9
输出: 0提示:
1 <= nums.length <= 3 * 104-104 <= nums[i] <= 1042 <= k <= 104
算法思路
补充两个小知识
- 同余定理
如果(a - b) % n == 0,那么我们可以得到一个结论:a % n == b % n。用文字叙述就是,如果两个数相减的差能被n整除,那么这两个数对n取模的结果相同。
例如:(26 - 2) % 12 == 0,那么26 % 12 == 2 % 12 == 2。 - c++ 中负数取模的结果,以及如何修正负数取模的结果
- c++ 中关于负数的取模运算,结果是把负数当成正数,取模之后的结果加上一个负号。
例如:-1 % 3 = -(1 % 3) = -1 - 因为有负数,为了防止发生出现负数的结果,以
(a % n + n) % n的形式输出保证为正。
例如:-1 % 3 = (-1 % 3 + 3) % 3 = 2
- c++ 中关于负数的取模运算,结果是把负数当成正数,取模之后的结果加上一个负号。
设 i 为数组中的任意位置,用 sum[i] 表示 [0, i] 区间内所有元素的和。
- 想知道有多少个以
i为结尾的可被k整除的子数组,就要找到有多少个起始位置为x1, x2, x3...使得[x, i]区间内的所有元素的和可被k整除。 - 设
[0, x - 1]区间内所有元素之和等于a,[0, i]区间内所有元素的和等于b,可得(b - a) % k == 0。 - 由同余定理可得,
[0, x - 1]区间与[0, i]区间内的前缀和同余。于是问题就变成:- 找到在
[0, i - 1]区间内,有多少前缀和的余数等于sum[i] % k的即可。
- 找到在
我们不用真的初始化一个前缀和数组,因为我们只关心在 i 位置之前,有多少个前缀和等于sum[i] - k 。因此,我们仅需用一个哈希表,一边求当前位置的前缀和,一边存下之前每一种前缀和出现的次数。
代码实现
class Solution {
public:int subarraysDivByK(vector<int>& nums, int k) {unordered_map<int, int> hash;hash[0%k] = 1;int sum = 0, ret = 0;for(auto &n : nums){sum += n;int r = (sum%k + k)%k;if(hash[r] > 0)ret+=hash[r];hash[r]++;} return ret;}
};

连续数组
题目链接
525. 连续数组
题目描述
给定一个二进制数组
nums, 找到含有相同数量的0和1的最长连续子数组,并返回该子数组的长度。
示例 1:
输入:nums = [0,1]
输出:2
说明:[0, 1] 是具有相同数量 0 和 1 的最长连续子数组。示例 2:
输入:nums = [0,1,0]
输出:2
说明:[0, 1] (或 [1, 0]) 是具有相同数量 0 和 1 的最长连续子数组。示例 3:
输入:nums = [0,1,1,1,1,1,0,0,0]
输出:6
解释:[1,1,1,0,0,0] 是具有相同数量 0 和 1 的最长连续子数组。
提示:
1 <= nums.length <= 105nums[i]不是0就是1
算法思路
稍微转化一下题目,就会变成我们熟悉的题:
- 本题让我们找出一段连续的区间,
0和1出现的次数相同。 - 如果将
0记为-1,1记为1,问题就变成了找出一段区间,这段区间的和等于0。
• 于是,就和 560. 和为 K 的子数组 这道题的思路一样
代码实现
class Solution {
public:int findMaxLength(vector<int>& nums) {unordered_map<int, int> hash;hash[0] = -1;int n = nums.size(), sum = 0, ret = 0;for(int i = 0; i < n; i++){sum += (nums[i] == 0 ? -1: 1);if(hash.count(sum))ret = max(ret, i - hash[sum]);else hash[sum] = i;}return ret;}
};

矩阵区域和
题目链接
1314. 矩阵区域和
题目描述
给你一个
m x n的矩阵mat和一个整数k,请你返回一个矩阵answer,其中每个answer[i][j]是所有满足下述条件的元素mat[r][c]的和:
i - k <= r <= i + k,j - k <= c <= j + k且(r, c)在矩阵内。示例 1:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出:[[12,21,16],[27,45,33],[24,39,28]]示例 2:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2
输出:[[45,45,45],[45,45,45],[45,45,45]]提示:
m == mat.lengthn == mat[i].length1 <= m, n, k <= 1001 <= mat[i][j] <= 100
算法思路
⼆维前缀和的简单应用题,关键就是我们在填写结果矩阵的时候,要找到原矩阵对应区域的左上角以及右下角的坐标(推荐画图)
- 左上角坐标:
x1 = i - k,y1 = j - k,但是由于会超过矩阵的范围,因此需要对0取一个max。因此修正后的坐标为:x1 = max(0, i - k),y1 = max(0, j - k); - 右下角坐标:
x1 = i + k,y1 = j + k,但是由于会超过矩阵的范围,因此需要对row - 1,以及col - 1取⼀个min。因此修正后的坐标为:x2 = min(row - 1, i + k),y2 = min(col - 1, j + k)。
然后将求出来的坐标代入到二维前缀和矩阵的计算公式上即可~(但是要注意下标的映射关系)
代码实现
class Solution {
public:vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {int row = mat.size(), col = mat[0].size();vector<vector<int>> dp(row+1, vector<int>(col+1));for(int i = 1; i <= row; i++)for(int j = 1; j <= col; j++)dp[i][j] = dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+mat[i-1][j-1];vector<vector<int>> answer(row, vector<int>(col));for(int i = 0; i < row; i++)for(int j = 0; j < col; j++){int x1 = max(0, i-k)+1, y1 = max(0, j-k)+1;int x2 = min(row-1, i+k)+1, y2 = min(col-1, j+k)+1;answer[i][j] = dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1];}return answer;}
};

⚠️ 写在最后:以上内容是我在学习以后得一些总结和概括,如有错误或者需要补充的地方欢迎各位大佬评论或者私信我交流!!!
相关文章:

算法思想之前缀和(二)
欢迎拜访:雾里看山-CSDN博客 本篇主题:算法思想之前缀和(二) 发布时间:2025.4.11 隶属专栏:算法 目录 算法介绍核心思想大致步骤 例题和为 K 的子数组题目链接题目描述算法思路代码实现 和可被 K 整除的子数组题目链接题目描述算法…...
)
C++ - 数据容器之 unordered_map(声明与初始化、插入元素、访问元素、遍历元素、删除元素、查找元素)
一、unordered_map unordered_map 是 C STL 中的一个关联容器,它有如下特点 unordered_map 存储键值对,使用哈希表实现 unordered_map 的每个键在容器中只能出现一次 unordered_map 的存储的键值对是无序的 平均情况下,查找、插入、删除都…...

六、分布式嵌入
六、分布式嵌入 文章目录 六、分布式嵌入前言一、先要配置torch.distributed环境二、Distributed Embeddings2.1 EmbeddingBagCollectionSharder2.2 ShardedEmbeddingBagCollection 三、Planner总结 前言 我们已经使用了TorchRec的主模块:EmbeddedBagCollection。我…...

硬件知识积累 单片机+ 光耦 + 继电器需要注意的地方
1. 电路图 与其数值描述 1.1 单片机引脚信号为 OPtoCoupler_control_4 PC817SB 为 光耦 继电器 SRD-05VDC-SL-A 的线圈电压为 67Ω。 2. 需注意的地方 1. 单片机的推挽输出的电流最大为 25mA 2. 注意光耦的 CTR 参数 3. 注意继电器线圈的 内阻 4. 继电器的开启电压。 因为光耦…...

Dockerfile 学习指南和简单实战
引言 Dockerfile 是一种用于定义 Docker 镜像构建步骤的文本文件。它通过一系列指令描述了如何一步步构建一个镜像,包括安装依赖、设置环境变量、复制文件等。在现实生活中,Dockerfile 的主要用途是帮助开发者快速、一致地构建和部署应用。它确保了应用…...

MCU屏和RGB屏
一、MCU屏 MCU屏:全称为单片机控制屏(Microcontroller Unit Screen),在显示屏背后集成了单片机控制器,因此,MCU屏里面有专用的驱动芯片。驱动芯片如:ILI9488、ILI9341、SSD1963等。驱动芯片里…...

Elasticsearch 向量数据库,原生支持 Google Cloud Vertex AI 平台
作者:来自 Elastic Valerio Arvizzigno Elasticsearch 将作为第一个第三方原生语义对齐引擎,支持 Google Cloud 的 Vertex AI 平台和 Google 的 Gemini 模型。这使得联合用户能够基于企业数据构建完全可定制的生成式 AI 体验,并借助 Elastics…...

蓝桥杯基础数论入门
一.试除法 首先我们要了解,所有大于1的自然数都能进行质因数分解。试除法作用如下: 质数判断 试除法通过验证一个数是否能被小于它的数(一般是用2到用根号x)整除来判断其是否为质数。根据定义,质数只能被1和自身整除…...

Spring 事件机制与观察者模式的深度解析
一、引言 在软件设计中,观察者模式(Observer Pattern)是一种非常经典且实用的设计模式。它允许一个对象(Subject)在状态发生改变时通知所有依赖它的对象(Observers),从而实现对象之…...

【软考系统架构设计师】信息安全技术基础知识点
1、 信息安全包括5个基本要素:机密性、完整性、可用性、可控性与可审查性。 机密性:确保信息不暴露给未授权的实体或进程。(采取加密措施) 完整性:只有得到允许的人才能修改数据,并且能够判断出数据是否已…...

Python编程快速上手 让繁琐工作自动化笔记
编程基础 字符串使用单引号...

2025年第十六届蓝桥杯省赛真题解析 Java B组(简单经验分享)
之前一年拿了国二后,基本就没刷过题了,实力掉了好多,这次参赛只是为了学校的加分水水而已,希望能拿个省三吧 >_< 目录 1. 逃离高塔思路代码 2. 消失的蓝宝思路代码 3. 电池分组思路代码 4. 魔法科考试思路代码 5. 爆破思路…...

Java 设计模式:策略模式详解
Java 设计模式:策略模式详解 策略模式(Strategy Pattern)是一种行为型设计模式,它定义了一系列算法,将每个算法封装起来,并使它们可以相互替换。策略模式让算法的变化独立于使用算法的客户端,从…...

什么是TensorFlow?
TensorFlow 是由 Google Brain 团队开发的开源机器学习框架,被广泛应用于深度学习和人工智能领域。它的基本概念包括: 1. 张量(Tensor):在 TensorFlow 中,数据以张量的形式进行处理。张量是多维数组的泛化…...

【3GPP核心网】【5G】精讲5G网络语音业务系统架构
1. 欢迎大家订阅和关注,精讲3GPP通信协议(2G/3G/4G/5G/IMS)知识点,专栏会持续更新中.....敬请期待! 目录 1. 音视频业务 2. 消息类业务 SMS over IMS SMS over NAS 3. 互联互通架构 3.1 音视频业务互通场景 3.2 5G 用户与 5G 用户互通 3.3 5G 用户与 4G 用户的互通…...
01-算法打卡-数组-二分查找-leetcode(704)-第一天
1 数组基础理论 数组是存放在连续内存空间上的相同数据结构的集合。数组可以通过下标索引快速获取数据,因为数组的存储空间是连续的所以在删除、更新数据的时候需要移动其他元素的地址。 下图是一个数组的案例图形:【内存连续、索引小标从0开始可…...

怎么看英文论文 pdf沉浸式翻译
https://arxiv.org/pdf/2105.09492 Immersive Translate Xournal打开...
:冯诺依曼结构)
Linux 进程基础(一):冯诺依曼结构
文章目录 一、冯诺依曼体系结构是什么?🧠二、冯诺依曼体系为何成为计算机组成的最终选择?(一)三大核心优势奠定主流地位(二)对比其他架构的不可替代性 三、存储分级:速度与容量的平衡…...

RabbitMQ 深度解析:从基础到高级应用的全面指南
🐰 RabbitMQ 深度解析:从基础到高级应用的全面指南 前言📘 一、RabbitMQ 简介⚙️ 二、核心特性可靠性 🔒灵活路由 🔄高可用性 🌐多协议支持 🌍多语言客户端 💻插件机制 ὐ…...

【图灵Python爬虫逆向】题七:千山鸟飞绝
题目背景 题目地址:https://stu.tulingpyton.cn/problem-detail/7/ 这一题为中等难度 打开控制台时会发现进入无限debug,可以通过右键点击"一律不在此处暂停"来绕过这个障碍。 一、请求与响应分析 1. 请求参数分析 首先观察网络请求&…...

ubuntu 2404 安装 vcs 2018
参考ubuntu 2204 安装 vcs 2018 系统信息 Ubuntu 24.04.2 LTS ubuntu和 安装后的 vcs 花费了 22G , 其中 "安装后的 vcs" 占13G预先配置 过程 和 2204 安装 vcs 2018 不同, 其他相同 // vm-tools 的安装, 不是虚拟机不需要 sudo apt-get update sudo apt-get inst…...

潇洒浪: Dify 上传自定义文件去除内容校验 File validation failed for file: re.json
Dify上传文件 添加其他文件类型如 my.myselfsuffix 上传成功 执行报错 File validation failed for file: re.json 解决办法 Notepad++ 搜索dify源码...

python-66-前后端分离之图书管理系统的Vue前端项目逐行分析
文章目录 1 App.vue的数据表格1.1 template部分1.1.1 div标签1.1.2 h1标签1.1.3 el-button标签1.1.4 el-table标签1.1.5 el-table-column标签1.1.6 表格中放置按钮1.2 script部分1.2.1 加载库和函数1.2.2 创建响应式数组1.2.3 创建getBooks函数1.2.4 onMounted函数1.2.5 创建ha…...

【实战手册】8000w数据迁移实践:MySQL到MongoDB的完整解决方案
🔥 本文将带你深入解析大规模数据迁移的实践方案,从架构设计到代码实现,手把手教你解决数据迁移过程中的各种挑战。 📚博主其他匠心之作,强推专栏: 小游戏开发【博主强推 匠心之作 拿来即用无门槛】文章目录 一、场景引入1. 问题背景2. 场景分析为什么需要消息队列?为…...

麒麟高级服务器操作系统内核升级
1. 确认系统及内核版本 使用uname -r命令查看当前系统内核版本 ,使用cat /etc/.productinfo等命令确认操作系统版本,以便后续操作适配。 2. 查看可用内核版本 运行sudo yum list kernel* ,该命令会列出当前 yum 源中可用的内核相关包及版本信息&#…...

OpenAI为抢跑AI,安全底线成牺牲品?
几年前,如果你问任何一个AI从业者,安全测试需要多长时间,他们可能会淡定地告诉你:“至少几个月吧,毕竟这玩意儿可能改变世界,也可能毁了它。”而现在,OpenAI用实际行动给出了一个新答案——几天…...

OpenCV 图形API(25)图像滤波-----均值滤波(模糊处理)函数blur()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 使用归一化的方框滤波器模糊图像。 该函数使用以下核来平滑图像: K 1 k s i z e . w i d t h k s i z e . h e i g h t [ 1 1 ⋯ …...

大模型——Crawl4AI入门指南
大模型——Crawl4AI入门指南 本快速入门指南介绍了Crawl4AI,涵盖了基本用法、先进功能(例如分块和提取策略)以及异步编程。用户将学习如何实现各种爬虫技术,包括截图、JSON提取和动态内容爬取。 1. 什么是Crawl4AI? Crawl4AI 是一个强大的异步网络爬虫库,旨在简化信息…...
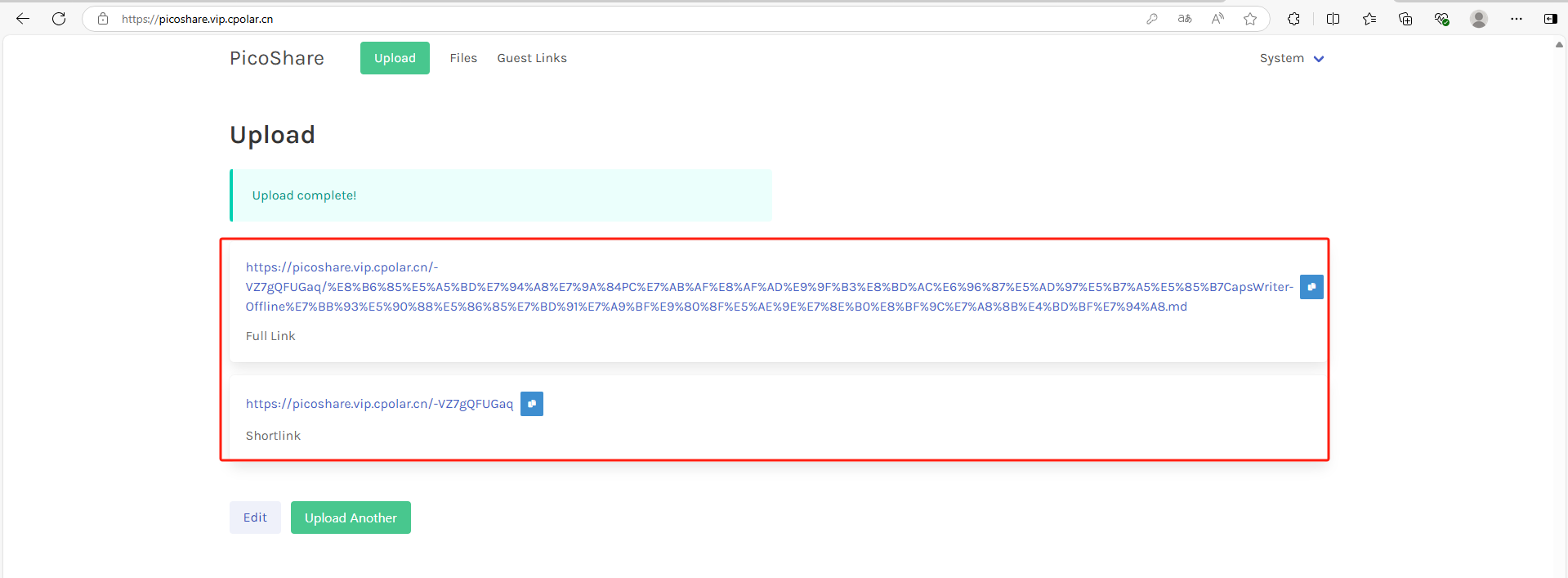
轻量级开源文件共享系统PicoShare本地部署并实现公网环境文件共享
## 前言 本篇文章介绍,如何在 Linux 系统本地部署轻量级文件共享系统 PicoShare,并结合 Cpolar 内网穿透实现公网环境远程传输文件至本地局域网内文件共享系统。 PicoShare 是一个由 Go 开发的轻量级开源共享文件系统,它没有文…...

UE5蓝图之间的通信------接口
一、创建蓝图接口 二、双击创建的蓝图接口,添加函数,并重命名新函数。 三、在一个蓝图(如玩家角色蓝图)中实现接口,如下图: 步骤一:点击类设置 步骤二:在细节面板已经实现的接口中…...
