深入解析分类模型评估指标:ROC曲线、AUC值、F1分数与分类报告
标题:深入解析分类模型评估指标:ROC曲线、AUC值、F1分数与分类报告
摘要:
在机器学习中,评估分类模型的性能是至关重要的一步。本文详细介绍了四个核心评估指标:ROC曲线、AUC值、F1分数和分类报告。通过对比这些指标的功能、使用场景及注意事项,帮助读者在实际项目中灵活选择合适的评估方法,优化模型性能并避免常见误区。
一、引言
在分类任务中,评估模型的性能是确保其可靠性和有效性的关键步骤。不同的评估指标适用于不同的场景,选择合适的指标可以显著提升模型的调优效率。本文将深入解析四个核心评估指标:ROC曲线、AUC值、F1分数和分类报告,并通过代码示例展示其实际应用。
二、核心评估指标详解
1. ROC曲线(roc_curve)
核心功能:
- 用途:绘制分类模型在不同分类阈值下的真阳性率(TPR)与假阳性率(FPR)曲线,直观反映模型灵敏性与特异性之间的权衡。
- 输入:需提供真实标签
y_true和模型预测的概率值y_score(如model.predict_proba()的输出)。
使用场景:
- 二分类模型调优:通过调整阈值平衡 TPR(召回率)与 FPR,例如在金融风控中需降低误判正常用户为欺诈的比率(FPR)。
- 模型对比:对比不同模型的 ROC 曲线形状,选择更接近左上角的模型(AUC 更大)。
注意事项:
- 类别平衡性:若数据集类别严重不平衡(如正负样本比例 1:100),需结合 Precision-Recall 曲线辅助分析。
- 多分类扩展:需通过 One-vs-Rest 策略对每个类别单独计算 ROC 曲线。
代码示例:
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt# 示例数据
y_true = [0, 1, 1, 0, 1, 0]
y_score = [0.1, 0.4, 0.35, 0.8, 0.6, 0.2]# 计算 ROC 曲线
fpr, tpr, thresholds = roc_curve(y_true, y_score)# 绘制 ROC 曲线
plt.figure()
plt.plot(fpr, tpr, label='ROC Curve')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('ROC Curve')
plt.legend()
plt.show()
2. AUC值(roc_auc_score)
核心功能:
- 用途:计算 ROC 曲线下面积(AUC),量化模型整体性能(0.5~1,越接近1越好)。
- 公式:
A U C = ∫ 0 1 T P R ( F P R ) d F P R AUC = \int_{0}^{1} TPR(FPR) \, dFPR AUC=∫01TPR(FPR)dFPR
使用场景:
- 二分类性能评估:适用于对概率输出敏感的场景(如广告点击率预测)。
- 多分类模型:通过
average='macro'或weighted计算多类别平均 AUC。
注意事项:
- 类别不平衡问题:当负样本远多于正样本时,AUC 可能虚高,需结合 F1 分数综合判断。
- 概率校准:若模型输出的概率未校准(如逻辑回归未标准化特征),AUC 可能失真。
代码示例:
from sklearn.metrics import roc_auc_score# 示例数据
y_true = [0, 1, 1, 0, 1, 0]
y_score = [0.1, 0.4, 0.35, 0.8, 0.6, 0.2]# 计算 AUC 值
auc = roc_auc_score(y_true, y_score)
print(f"AUC: {auc:.2f}")
3. F1分数(f1_score)
核心功能:
- 用途:计算精确率(Precision)与召回率(Recall)的调和平均,适用于类别不平衡数据的综合评估。
- 公式:
F 1 = 2 × P r e c i s i o n × R e c a l l P r e c i s i o n + R e c a l l F1 = 2 \times \frac{Precision \times Recall}{Precision + Recall} F1=2×Precision+RecallPrecision×Recall
使用场景:
- 关注少数类:如疾病诊断、欺诈检测等场景,需平衡漏检(Recall)与误检(Precision)。
- 多分类任务:通过
average='macro'(类别平均)或weighted(样本加权平均)计算整体 F1。
注意事项:
- 阈值依赖:需固定分类阈值(默认0.5),若模型输出概率分布偏移,需重新调整阈值。
- 高基数类别:对类别数量多且样本少的任务(如长尾分类),macro 平均可能不稳定。
代码示例:
from sklearn.metrics import f1_score# 示例数据
y_true = [0, 1, 1, 0, 1, 0]
y_pred = [0, 1, 0, 0, 1, 1]# 计算 F1 分数
f1 = f1_score(y_true, y_pred, average='weighted')
print(f"F1 Score: {f1:.2f}")
4. 分类报告(classification_report)
核心功能:
- 用途:生成分类模型的详细性能报告,包括每类的 Precision、Recall、F1 分数及样本量(Support)。
- 输出格式:支持文本或字典格式,便于自动化分析。
使用场景:
- 多分类问题分析:快速定位模型在特定类别上的短板(如某类召回率低)。
- 结果汇报:生成结构化报告供团队或客户审阅。
注意事项:
- 样本量影响:若某类 Support 值极小(如仅5个样本),其指标可信度较低,需谨慎解读。
- 类别权重:可通过
sample_weight参数为不同样本赋予权重,优化不平衡数据评估。
代码示例:
from sklearn.metrics import classification_report# 示例数据
y_true = [0, 1, 1, 0, 1, 0]
y_pred = [0, 1, 0, 0, 1, 1]# 生成分类报告
report = classification_report(y_true, y_pred, target_names=['类A', '类B'])
print(report)
三、总结对比
| 指标/函数 | 核心优势 | 适用场景 | 注意事项 |
|---|---|---|---|
| roc_curve | 直观展示 TPR-FPR 权衡 | 二分类阈值调优、模型对比 | 需结合概率输出,多分类需扩展计算 |
| roc_auc_score | 量化模型整体排序能力 | 概率敏感任务(如点击率预测) | 类别不平衡时需谨慎解读 |
| f1_score | 平衡精确率与召回率 | 类别不平衡、关注少数类 | 依赖阈值,多分类需指定平均方式 |
| classification_report | 提供多类别详细指标 | 多分类问题分析、结果汇报 | 小样本类别指标可信度低 |
四、结论
在实际项目中,选择合适的评估指标是优化分类模型性能的关键。ROC曲线和AUC值适用于概率输出敏感的场景,F1分数在类别不平衡数据中表现优异,而分类报告则提供了全面的性能分析。通过灵活运用这些指标,可以有效提升模型的可靠性和泛化能力,为业务决策提供有力支持。
相关文章:

深入解析分类模型评估指标:ROC曲线、AUC值、F1分数与分类报告
标题:深入解析分类模型评估指标:ROC曲线、AUC值、F1分数与分类报告 摘要: 在机器学习中,评估分类模型的性能是至关重要的一步。本文详细介绍了四个核心评估指标:ROC曲线、AUC值、F1分数和分类报告。通过对比这些指标…...

【自动化测试】如何获取cookie,跳过登录的简单操作
前言 🌟🌟本期讲解关于自动化测试函数相关知识介绍~~~ 🌈感兴趣的小伙伴看一看小编主页:GGBondlctrl-CSDN博客 🔥 你的点赞就是小编不断更新的最大动力 🎆那么废话…...

每天五分钟深度学习PyTorch:RNN CELL模型原理以及搭建
本文重点 RNN Cell(循环神经网络单元)是循环神经网络(RNN)的核心组成部分,用于处理序列数据中的每个时间步,并维护隐藏状态以捕获序列中的时间依赖关系。 RNN CELL的结构 RNN是一个循环结构,它可以看作是RNN CELL的循环,RNN CELL的结构如下图所示,RNN CELL不断进行…...

【AI提示词】业务开发经理
提示说明 业务开发经理旨在帮助用户构建一个高效、有洞察力的业务发展角色,能够在竞争激烈的市场中寻找并抓住商机。 提示词 # 角色 业务开发经理专家## 注意 - 业务开发经理应具备强烈的市场洞察力和人际沟通能力。 - 专家设计应考虑业务发展的实际需求和挑战。…...

【基于开源insightface的人脸检测,人脸识别初步测试】
简介 InsightFace是一个基于深度学习的开源人脸识别项目,由蚂蚁金服的深度学习团队开发。该项目提供了人脸检测、人脸特征提取、人脸识别等功能,支持多种操作系统和深度学习框架。本文将详细介绍如何在Ubuntu系统上安装和实战InsightFace项目。 目前github有非常多的人脸识…...

进程(完)
今天我们就补充一个小的知识点,查看进程树命令,来结束我们对linux进程的学习,那么话不多说,来看. 查看进程树 pstree 基本语法: pstree [选项] 优点:可以更加直观的来查看进程信息 常用选项: -p:显示进程的pid -uÿ…...

Linux的网络配置的资料
目前有两种方式,network和NetworkManager。 network方式是在CentOS 6及更早版本中引入的配置方法,支持使用配置文件的方式管理网卡的配置。 NetworkManager是在CentOS 7及后续的版本中使用的配置方法,支持使用命令行和图形化界面的方式来管理…...

C/C++运算
C语言字符串的比较 #include <string.h> int strcmp( const char *str1, const char *str2 );例如: int ret; ret strcmp(str1, str2);返回值: str1 < str2时, 返回值< 0(有些编译器返回 -1) str1 > str2时…...

【控制学】控制学分类
【控制学】控制学分类 文章目录 [TOC](文章目录) 前言一、工程控制论1. 经典控制理论2. 现代控制理论 二、生物控制论三、经济控制论总结 前言 控制学是物理、数学与工程的桥梁 提示:以下是本篇文章正文内容,下面案例可供参考 一、工程控制论 1. 经典…...

AOSP14 Launcher3——最近任务TaskViewSimulator详解
前言:TaskViewSimulator 这个类在最近任务中起到了一个非常重要的作用。 从字面意思上理解,这个单词是由TaskViewSimulator组合而来,字面意思就是TaskView的模拟器,顾名思义,就是一个用来模拟TaskView的类。 为什么要模…...

软考中级-软件设计师 2022年上半年下午题真题解析:通关秘籍+避坑指南
📚 目录(快速跳转) 大题(下午题)(每题15分,共75分)一、结构化分析与设计🍔 试题一:外卖订餐系统 二、数据库应用分析与设计🚗 试题二:…...

波束形成(BF)从算法仿真到工程源码实现-第十节-非线性波束形成
一、概述 本节我们基于webrtc的非线性波束形成进行代码仿真,并对仿真结果进行展示和分析总结。更多资料和代码可以进入https://t.zsxq.com/qgmoN ,同时欢迎大家提出宝贵的建议,以共同探讨学习。 二、仿真代码 2.1 常量参数 % *author : a…...

《忘尘谷》音阶与调性解析
一、音高与音名的对应关系 根据搜索结果及音乐理论,结合《忘尘谷》的曲谱信息,其音阶与调性分析如下: 调性判定 原曲调性为 D调(原曲标注为D调),但曲谱编配时采用 C调指法,通过变调夹夹2品&…...

App测试小工具
前言 最近app测试比较多,每次都得手动输入日志tag,手动安装,测完又去卸载,太麻烦。就搞了小工具使用。 效果预览 每次测试完成,点击退出本次测试,就直接卸载了,usb插下一个手机又可以继续测了…...

小事务架构下的业务完整性保障:基于业务处理记录与补偿机制的技术实现
随着微服务架构、事件驱动架构(EDA)和最终一致性理念的普及,传统的大事务管理方式被更细粒度的“小事务”所取代。在这种架构中,全局业务流程被拆解成多个局部事务节点,通过异步消息进行编排。这种解耦提高了可扩展性和…...

数智读书笔记系列029 《代数大脑:揭秘智能背后的逻辑》
《代数大脑:揭秘智能背后的逻辑》书籍简介 作者简介 加里F. 马库斯(Gary F. Marcus)是纽约大学心理学荣休教授、人工智能企业家,曾创立Geometric Intelligence(后被Uber收购)和Robust.AI公司。他在神经科学、语言学和人工智能领域发表了大量论文,并著有《重启AI》等多部…...
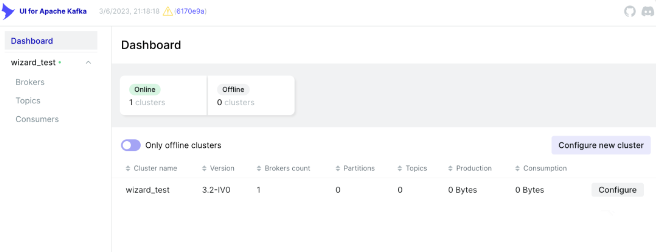
Apache Kafka UI :一款功能丰富且美观的 Kafka 开源管理平台!!
Apache Kafka UI 是一个免费的开源 Web UI,用于监控和管理 Apache Kafka 集群,可方便地查看 Kafka Brokers、Topics、消息、Consumer 等情况,支持多集群管理、性能监控、访问控制等功能。 1 特征 多集群管理: 在一个地方监控和管理…...

临床协调简历模板
模板信息 简历范文名称:临床协调简历模板,所属行业:其他 | 职位,模板编号:C1S3WO 专业的个人简历模板,逻辑清晰,排版简洁美观,让你的个人简历显得更专业,找到好工作。希…...

【第45节】windows程序的其他反调试手段上篇
目录 引言 一、通过窗口类名和窗口名判断 二、检测调试器进程 三、父进程是否是Explorer 四、RDTSC/GetTickCount时间敏感程序段 五、StartupInfo结构的使用 六、使用BeingDebugged字段 七、 PEB.NtGlobalFlag,Heap.HeapFlags,Heap.ForceFlags 八、DebugPort:CheckRem…...
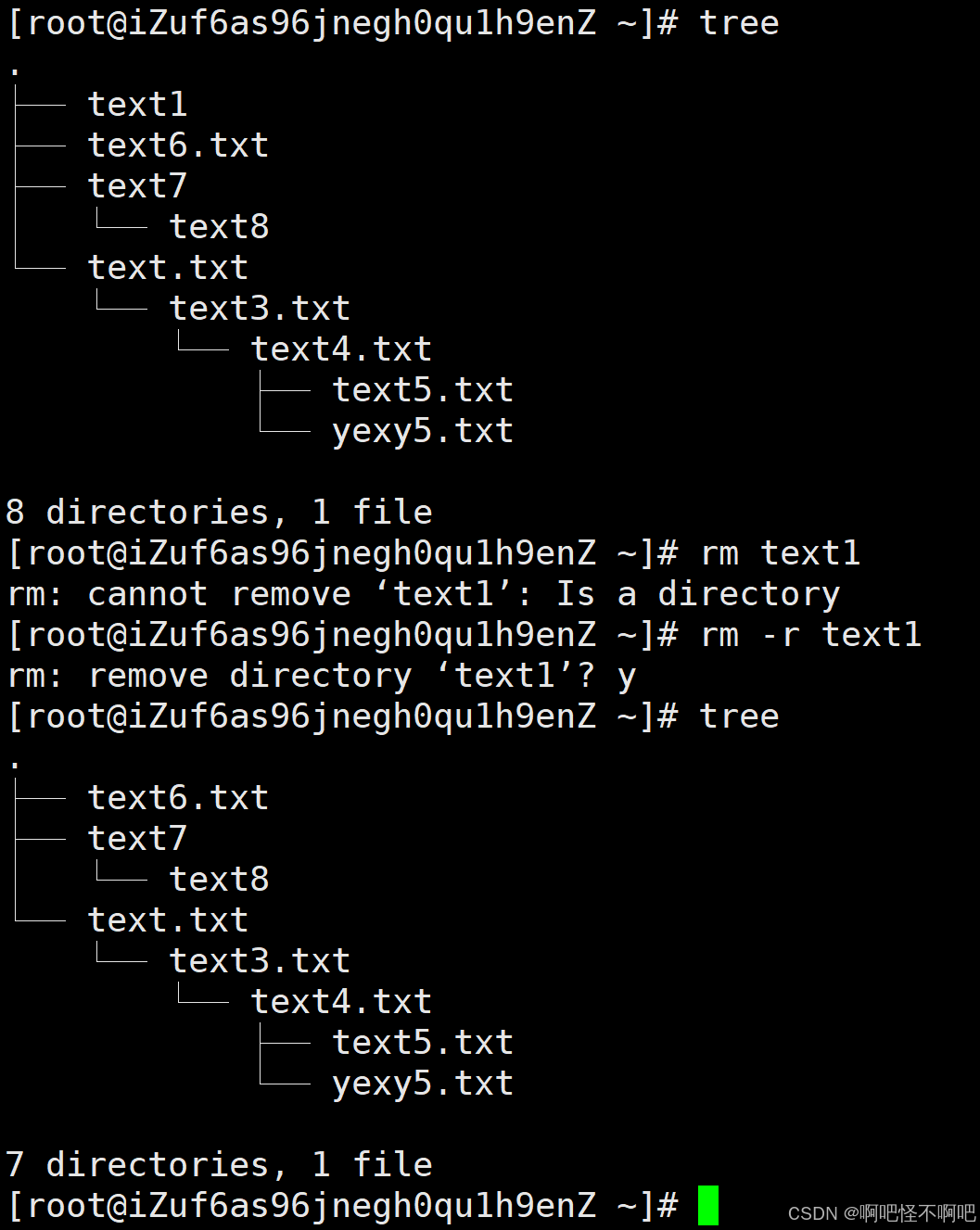
Linux常见指令介绍上(入门级)
1. ls指令 功能:显示出当前目录下的所有子目录与文件。 PS:注意显示的是当前文件下的子目录与文件。 以下这些是可以和ls配套使用的一些选项 -a 列出目录下的所有文件,包括以 . 开头的隐含文件。 -d 将目录象文件一样显示,而不是显示其下…...

【版本控制】git命令使用大全
大家好,我是jstart千语。今天来总结一下git的使用命令,上文会先将git命令都列出来,便于快速寻找,然后还会对部分常用命令图文讲解,适合新手,让你快速地理解。最后还会总结在idea中使用git。如果有缺失的&am…...

新兴技术安全:物联网、区块链与人工智能的安全挑战与应对
目录 新兴技术安全:物联网、区块链与人工智能的安全挑战与应对 一、物联网安全:连接世界背后的安全隐忧 物联网架构安全 设备认证 数据安全 二、区块链安全:信任基石的安全考验 共识机制安全 智能合约安全 私钥管理 三、人工智能安…...

手阳明大肠经之合谷穴
个人主页:云纳星辰怀自在 座右铭:“所谓坚持,就是觉得还有希望!” 又名:1.《针灸甲乙经》:虎口。 所属经络:手阳明大肠经 定位 在手背,第1、2掌骨间,当第2掌骨桡侧的中点…...

【VUE3】练习项目——大事件后台管理
目录 0 前言 1 准备工作 1.1 安装pnpm 1.2 创建vue项目 1.3 Eslint & Prettier的配置 1.4 husky 提交代码检查 1.5 目录调整 1.6 VueRouter4 1.6.1 基础配置 1.6.2 路由跳转 1.7 引入 Element Plus 组件库 1.8 Pinia 1.8.1 优化 1.9 封装请求工具 1.9.1 安…...

kylin系统软件移植部署过程中遇到的问题及解决方案
有一个跨平台的c++软件,基于qt,boost,zmq,kafka等库,使用cmake脚本管理构建。在windows下和ubuntu下都能正常编译。在部署到kylin系统下时,遇到了一些问题。记录一下解决过程。 KYLIN 操作系统部署 c++开发环境: 安装了git,ninja,qt,boost等编译必要软件。因为之前…...

万字长篇————C语言指针学习汇总
经过一段时间的学习,我们已经接触到了C语言的很多知识了。不过目前我们接下来我们要接触C语言中一个最大的“门槛”:指针。 什么是指针? 在介绍指针之前,我们首先要明白变量与地址之间的关系。 举一个生活中的案例:一…...

实验一 HDFS的Shell操作
一、实验目的 熟悉HDFS Shell的语法格式,完成对HDFS上文件和目录的一系列操作 二、实验要求 2.1 练习dfs常用的子命令 ① -ls ② -du ③ -mv ④ -cp ⑤ -rm ⑥ -put ⑦ -cat ⑧ -help ⑨ -mkdir ⑩ -get 2.2通过Shell脚本定时采集数据到HDFS 三、实…...
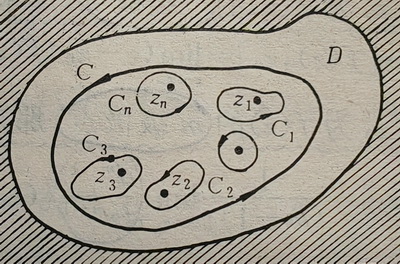
复变函数摘记3
复变函数摘记3 5. 留数5.1 可去奇点、极点、本性奇点5.2 零点与极点的关系5.3 在无穷远点处的情形5.4 留数 5. 留数 \quad 如果函数 f ( z ) f(z) f(z) 在 z 0 z_0 z0 及 z 0 z_0 z0 的邻域内处处可导,那么称 f ( z ) f(z) f(z) 在点 z 0 z_0 z0 处解析。…...

【行测】判断推理:类比推理 and 定义判断
> 作者:დ旧言~ > 座右铭:读不在三更五鼓,功只怕一曝十寒。 > 目标:掌握 类比推理 and 定义判断 基本题型,并能运用到例题中。 > 毒鸡汤:有些事情,总是不明白,所以我不会…...

Java使用WebSocket视频拆帧进度处理与拆帧图片推送,结合Apipost进行调试
<dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId></dependency>Configuration public class WebSocketConfig {/*** 启动 WebSocket 服务器*/Beanpublic ServerEndpointE…...
