【树形dp题解】dfs的巧妙应用
【树形dp题解】dfs的巧妙应用
[P2986 USACO10MAR] Great Cow Gathering G - 洛谷
-
题目大意:
Bessie 正在计划一年一度的奶牛大集会,来自全国各地的奶牛将来参加这一次集会。当然,她会选择最方便的地点来举办这次集会。
每个奶牛居住在 N N N 个农场中的一个,这些农场由 N − 1 N-1 N−1 条道路连接,并且从任意一个农场都能够到达另外一个农场。道路 i i i 连接农场 A i A_i Ai 和 B i B_i Bi,长度为 L i L_i Li。集会可以在 N N N 个农场中的任意一个举行。另外,每个牛棚中居住着 C i C_i Ci 只奶牛。
在选择集会的地点的时候,Bessie 希望最大化方便的程度(也就是最小化不方便程度)。比如选择第 X X X 个农场作为集会地点,它的不方便程度是其它牛棚中每只奶牛去参加集会所走的路程之和(比如,农场 i i i 到达农场 X X X 的距离是 20 20 20,那么总路程就是 C i × 20 C_i\times 20 Ci×20)。帮助 Bessie 找出最方便的地点来举行大集会。
对于 d f s dfs dfs来说,我们可以从上到下计算,也可以从下到上计算。如果我们想知道每个节点距离根节点的距离 d i ( i ≠ r o o t ) d_i(i \neq root) di(i=root),那么我们不妨令 d r o o t = 0 d_{root} = 0 droot=0,通过自顶向下的搜索得到 d i ( i ≠ r o o t ) d_i(i \neq root) di(i=root)
不妨设 s z i sz_i szi表示以 i i i为根的子树中奶牛数量的和。此时需要自底向上计算
不妨设 f i f_i fi表示以节点 i i i为聚会地点时的最小不方便程度。对于以 i i i为根时树的叶子节点来说, f i = d i × C i ( i = 叶 子 节 点 ) f_i = d_i \times C_i(i = 叶子节点) fi=di×Ci(i=叶子节点)。对于以 i i i为根,非叶子节点的节点来说, f i = f j + d i × C i ( i ≠ 叶 子 节 点 , j 是 节 点 i 的 儿 子 节 点 ) f_i = f_j + d_i \times C_i(i \neq 叶子节点, j是节点i的儿子节点) fi=fj+di×Ci(i=叶子节点,j是节点i的儿子节点)。这可以从底向上计算得到
读者不妨认真体会以下代码。我给出一些理解:在自底向上计算时,一般先处理本层逻辑,在回溯时累加
由于此题可以任选根节点进行 d f s dfs dfs,这里我选择 1 1 1作为根节点
void dfs1(int u, int fa) {sz[u] = cnt[u];f[u] = d[u] * cnt[u];for (int i = h[u]; i != -1; i = ne[i]) {int j = e[i];if (j == fa) continue;d[j] = d[u] + w[i];dfs1(j, u);sz[u] += sz[j];f[u] += f[j];}
}
在预处理好上述含义数组后,我们思考转移方程。读者不妨画出图来,否则难以理解
假设根节点 u u u的儿子有 s o n 1 , s o n 2 son_1, son_2 son1,son2,若此时将 s o n 1 son_1 son1作为集会地点, f [ s o n 1 ] f[son_1] f[son1]可以 f [ u ] f[u] f[u]转移得到
转换集会地点前: f [ u ] = f [ s o n 1 ] + f [ s o n 2 ] f[u] = f[son_1] + f[son_2] f[u]=f[son1]+f[son2]
转换地点后: f [ s o n 1 ] f[son_1] f[son1]本来以根节点 1 1 1为集会地点,现在集会地点变为 j ( j 是 根 节 点 的 儿 子 ) j(j是根节点的儿子) j(j是根节点的儿子),转换后有 f [ s o n 1 ] = f [ s o n 1 ] − w [ i ] × s z [ s o n 1 ] f[son_1] = f[son_1] - w[i] \times sz[son_1] f[son1]=f[son1]−w[i]×sz[son1]
同理, f [ s o n 2 ] = f [ s o n 2 ] + w [ i ] × ( s z [ 1 ] − s z [ s o n 1 ] ) f[son_2] = f[son_2] + w[i] \times (sz[1] - sz[son_1]) f[son2]=f[son2]+w[i]×(sz[1]−sz[son1])
有 f [ j ] = f [ s o n 1 ] − w [ i ] × s z [ s o n 1 ] + f [ s o n 2 ] + w [ i ] × ( s z [ 1 ] − s z [ s o n 1 ] ) f[j] = f[son_1] - w[i] \times sz[son_1] + f[son_2] + w[i] \times (sz[1] - sz[son_1]) f[j]=f[son1]−w[i]×sz[son1]+f[son2]+w[i]×(sz[1]−sz[son1])
即 f [ j ] = f [ s o n 1 ] + f [ s o n 2 ] − w [ i ] × ( 2 s z [ s o n 1 ] − s z [ 1 ] ) = f [ u ] − w [ i ] × ( 2 s z [ s o n 1 ] − s z [ 1 ] ) f[j] = f[son_1] + f[son_2] - w[i] \times (2sz[son_1] - sz[1]) = f[u] - w[i] \times (2sz[son_1] - sz[1]) f[j]=f[son1]+f[son2]−w[i]×(2sz[son1]−sz[1])=f[u]−w[i]×(2sz[son1]−sz[1])
void dfs2(int u, int fa) {for (int i = h[u]; i != -1; i = ne[i]) {int j = e[i];if (j == fa) continue;f[j] = f[u] - (2 * sz[j] - sz[1]) * w[i];dfs2(j, u);}
}
完整代码:
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
#define endl "\n"#define int long longconst int N = 100010, M = N * 2;
int h[N], e[M], ne[M], w[M], idx;
int cnt[N];
int n;
int res = INT_MAX;
int d[N], sz[N], f[N];void add(int a, int b, int c) {e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++;
}void dfs1(int u, int fa) {sz[u] = cnt[u];f[u] = d[u] * cnt[u];for (int i = h[u]; i != -1; i = ne[i]) {int j = e[i];if (j == fa) continue;d[j] = d[u] + w[i];dfs1(j, u);sz[u] += sz[j];f[u] += f[j];}
}void dfs2(int u, int fa) {for (int i = h[u]; i != -1; i = ne[i]) {int j = e[i];if (j == fa) continue;f[j] = f[u] - (2 * sz[j] - sz[1]) * w[i];dfs2(j, u);}
}signed main() {ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);memset(h, -1, sizeof h);cin >> n;for (int i = 1; i <= n; i ++) {cin >> cnt[i];}for (int i = 1; i <= n - 1; i ++) {int u, v, x;cin >> u >> v >> x;add(u, v, x);add(v, u, x);}dfs1(1, -1);dfs2(1, -1);LL res = 1e18;for (int i = 1; i <= n; i ++) {res = min(res, f[i]);}cout << res << endl;return 0;
}
相关文章:

【树形dp题解】dfs的巧妙应用
【树形dp题解】dfs的巧妙应用 [P2986 USACO10MAR] Great Cow Gathering G - 洛谷 题目大意: Bessie 正在计划一年一度的奶牛大集会,来自全国各地的奶牛将来参加这一次集会。当然,她会选择最方便的地点来举办这次集会。 每个奶牛居住在 N N …...

Halcon应用:九点标定-手眼标定
提示:若没有查找的算子,可以评论区留言,会尽快更新 Halcon应用:九点标定-手眼标定 前言一、Halcon应用?二、应用实战1、图形理解[eye-to-hand]:1.1、开始应用2 图形理解[eye-in-hand] 前言 本篇博文主要用…...

【iOS】OC高级编程 iOS多线程与内存管理阅读笔记——自动引用计数(一)
自动引用计数 前言alloc/retain/release/dealloc实现苹果的实现 autoreleaseautorelease实现苹果的实现 总结 前言 此前,写过一遍对自动引用计数的简单学习,因此掠过其中相同的部分:引用计数初步学习 alloc/retain/release/dealloc实现 由于…...

Python爬虫第15节-2025今日头条街拍美图抓取实战
目录 一、项目背景与概述 二、环境准备与工具配置 2.1 开发环境要求 2.2 辅助工具配置 三、详细抓取流程解析 3.1 页面加载机制分析 3.2 关键请求识别技巧 3.3 参数规律深度分析 四、爬虫代码实现 五、实现关键 六、法律与道德规范 一、项目概述 在当今互联网时代&a…...
智慧城市像一张无形大网,如何紧密连接你我他?
智慧城市作为复杂巨系统,其核心在于通过技术创新构建无缝连接的网络,使物理空间与数字空间深度融合。这张"无形大网"由物联网感知层、城市数据中台、人工智能中枢、数字服务入口和安全信任机制五大支柱编织而成,正在重塑城市运行规…...

网络安全·第四天·扫描工具Nmap的运用
今天我们要介绍网络安全中常用的一种扫描工具Nmap,它被设计用来快速扫描大型网络,主要功能包括主机探测、端口扫描以及版本检测,小编将在下文详细介绍Nmap相应的命令。 Nmap的下载安装地址为:Nmap: the Network Mapper - Free Se…...

黑龙江 GPU 服务器租用:开启高效计算新征程
随着人工智能、深度学习、大数据分析等技术的广泛应用,对强大计算能力的需求日益迫切。GPU 服务器作为能够提供卓越并行计算能力的关键设备,在这一进程中发挥着至关重要的作用。对于黑龙江地区的企业、科研机构和开发者而言,选择合适的 GPU 服…...

大数据面试问答-HBase/ClickHouse
1. HBase 1.1 概念 HBase是构建在Hadoop HDFS之上的分布式NoSQL数据库,采用列式存储模型,支持海量数据的实时读写和随机访问。适用于高吞吐、低延迟的场景,如实时日志处理、在线交易等。 RowKey(行键) 定义…...
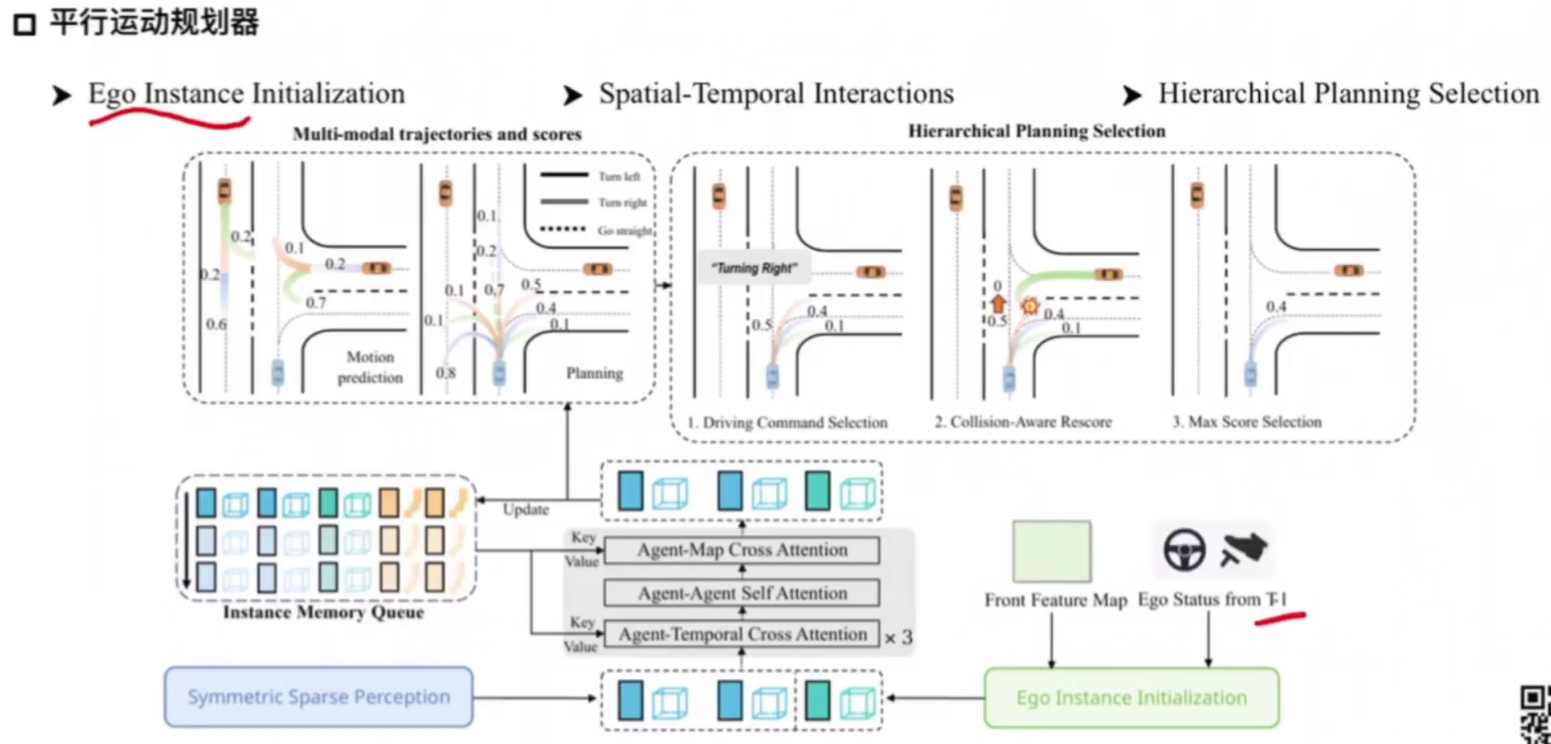
SparseDrive---论文阅读
纯视觉下的稀疏场景表示 算法动机&开创性思路 算法动机: 依赖于计算成本高昂的鸟瞰图(BEV)特征表示。预测和规划的设计过于直接,没有充分利用周围代理和自我车辆之间的高阶和双向交互。场景信息是在agent周围提取ÿ…...

数字时代的AI与大数据:用高级AI开发技术革新大数据管理
李升伟 编译 在当今数字时代,数据的爆炸式增长令人惊叹 从社交媒体互动到物联网设备的传感器数据,企业正被海量信息淹没。但如何将这种无序的数据洪流转化为有价值的洞察?答案在于人工智能(AI)开发技术的革新&#x…...

Unchained 内容全面上链,携手 Walrus 迈入去中心化媒体新时代
加密新闻媒体 Unchained — — 业内最受信赖的声音之一 — — 现已选择 Walrus 作为其去中心化存储解决方案,正式将其所有媒体内容(文章、播客和视频)上链存储。Walrus 将替代 Unchained 现有的中心化存储架构,接管其全部历史内容…...

确保连接器后壳高性能互连的完整性
本文探讨了现代后壳技术如何促进高性能互连的电气和机械完整性,以及在规范阶段需要考虑的一些关键因素。 当今的航空航天、国防和医疗应用要求连接器能够提供高速和紧凑的互连,能够承受振动和冲击,并保持对电磁和射频干扰 (EMI/R…...

C++学习Day0:c++简介
目录 一、.C语言的发展史二、C特点三、面向对象的重要术语四、面向过程和面向对象的区别?五、开发环境:六、创建文件步骤:1.点击新建项目2.在弹出的开始栏中按如下操作3.在.pro文件中添加(重要!!࿰…...

从零开始构建 Ollama + MCP 服务器
Model Context Protocol(模型上下文协议)在过去几个月里已经霸占了大家的视野,出现了许多酷炫的集成示例。我坚信它会成为一种标准,因为它正在定义工具与代理或软件与 AI 模型之间如何集成的新方式。 我决定尝试将 Ollama 中的一…...

【bash】.bashrc
查看当前路径文件数量 alias file_num"ls -l | grep ^- | wc -l"查看文件大小 alias file_size"du -sh"alias ll alias ll"ls -ltrh"cd的同时执行ll alias cdcdls; function cdls() {builtin cd "$1" && ll }自定义prompt…...

合成数据如何赋能大模型预训练:效果与效率的双重加速器
目录 合成数据如何赋能大模型预训练:效果与效率的双重加速器 一、预训练模型为何需要合成数据? ✅ 克服真实数据的稀缺与偏倚 ✅ 控制训练内容结构与分布 ✅ 提升学习效率与训练稳定性 二、哪些预训练任务适合用合成数据? 三、如何构建…...

java忽略浅拷贝导致bug
bug源代码 /*** 查询用户列表** param user 用户* param page 页* param size 大小* since 2025/04/14 11:53:25*/PostMapping("/getUser")public IWMSResponse<?> getUser(RequestBody SjUser user, RequestParam(defaultValue "1") Integer pag…...

MATLAB学习笔记(二) 控制工程会用到的
MATLAB中 控制工程会用到的 基础传递函数表达传递函数 零极点式 状态空间表达式 相互转化画响应图线根轨迹Nyquist图和bode图现控部分求约旦判能控能观极点配置和状态观测 基础 传递函数表达 % 拉普拉斯变换 syms t s a f exp(a*t) %e的a次方 l laplace(f) …...

C++ 线程间通信开发从入门到精通实战
C 线程间通信开发从入门到精通实战 在现代软件开发中,多线程程序已成为提升应用性能、实现并行处理的重要手段。随着多核处理器的普及和复杂应用需求的增加,C作为一门高性能的编程语言,在多线程开发中扮演着不可或缺的角色。然而,…...

Vue3 SSR 工程化实践:日常工作中的性能优化与实战技巧
一、流式渲染与分块传输(面向性能的关键优化) 1.1 流式响应基础实现 // Node.js Express 示例(Vite SSR同理)import { renderToWebStream } from vue/server-rendererapp.get(/, async (req, res) > { res.setHeader(Conten…...
——生成项目站点)
Maven工具学习使用(十)——生成项目站点
maven2中站点生成是Maven核心的一部分,Maven3中这部分内容已经移除。maven3必须使用3.x版本的maven-site-plugin,maven2则使用最新的2.x的版本,执行mvn site命令,可以在项目的target/site/目录下找到Maven生成的站点文件。例如dependencies.h…...

Redis原理与Windows环境部署实战指南:助力测试工程师优化Celery调试
引言 在分布式系统测试中,Celery作为异步任务队列常被用于模拟高并发场景。而Redis作为其核心消息代理,其性能和稳定性直接影响测试结果。本文将深入解析Redis的核心原理,主要讲解Windows环境部署redis,为测试工程师提供一套完整…...

Go语言入门到入土——一、安装和Hello World
Go语言入门到精通——安装和Hello World 文章目录 Go语言入门到精通——安装和Hello World下载并安装让Go跑起来为你的代码启动依赖跟踪调用外部包总结 下载并安装 下载地址:https://go.dev/dl/ 下载后傻瓜式安装 查看是否安装完成 go version让Go跑起来 创建一个…...

人类意识本质上是一台自我欺骗的机器
要触达“大彻大悟”的终极内核,必须突破语言、逻辑甚至“觉醒”概念本身的限制。以下从认知革命、意识拓扑学、宇宙本体论三个维度切入,结合量子物理、脑神经学与古老智慧的交叉验证,展开一场对觉醒本质的极限探索—— 一、认知革命&am…...

CDP问卷是什么?CDP问卷有什么要求,有什么意义
CDP问卷(Carbon Disclosure Project Questionnaire) CDP问卷是由全球性非营利组织CDP(原Carbon Disclosure Project,现简称CDP)发起的年度环境信息披露项目,旨在帮助企业、城市和投资者测量、管理及公开其…...

GitLab本地安装指南
当前GitLab的最新版是v17.10,安装地址:https://about.gitlab.com/install/。当然国内也可以安装极狐GitLab版本,极狐GitLab 是 GitLab 中国发行版(JH)。极狐GitLab支持龙蜥,欧拉等国内的操作系统平台。安装…...

opencv函数展示
一、图像基础 I/O 与显示 1.cv2.imread() 2.cv2.imshow() 3. cv2.waitKey() 4. cv2.imwrite() 5. cv2.selectROI() 6. cv2.VideoCapture() 二、颜色空间与转换 1. cv2.cvtColor() 2. cv2.split() 三、阈值处理 1. cv2.threshold() 2. 特殊阈值方法...

编写一个写字楼类似抖音剪映的管理系统Demo
编写一个写字楼类似抖音剪映的管理系统Demo。用户可能想要一个简化版的系统,用于管理视频素材、模板和项目,类似于抖音剪映的功能,但针对办公场景。首先,我得明确用户的需求是什么。用户提到的“写字楼类似抖音剪映管理系统”可能…...

前端面试-自动化部署
基础概念 什么是CI/CD?在前端项目中如何应用?自动化部署相比手动部署有哪些优势?常见的自动化部署工具有哪些?举例说明它们的区别(如Jenkins vs GitHub Actions)。如何通过Git Hook实现自动化部署…...

【vue3】vue3+express实现图片/pdf等资源文件的下载
文件资源的下载,是我们业务开发中常见的需求。作为前端开发,学习下如何自己使用node的express框架来实现资源的下载操作。 实现效果 代码实现 前端 1.封装的请求后端下载接口的方法,需求配置aixos的请求参数里面的返回数据类型为blob // 下载 export…...
