数据结构实验7.2:二叉树的基本运算
文章目录
- 一,实验目的
- 二,问题描述
- 三,基本要求
- 四,实验操作
- 五,示例代码
- 六,运行效果
一,实验目的
- 深入理解树与二叉树的基本概念,包括节点、度、层次、深度等,清晰区分二叉树与一般树的结构特点,为后续学习和应用打下坚实基础。
- 熟练掌握用递归方法实现二叉树的遍历,通过递归算法的设计和实现,深刻体会递归思想在处理树结构数据时的简洁性和高效性,提高对递归算法的运用能力。
- 掌握借助栈或队列实现二叉树遍历的非递归迭代方法,理解栈和队列在模拟递归过程中的作用,培养利用数据结构解决问题的能力,拓宽算法设计思路。
- 熟练掌握构造Huffman树、Huffman编码等操作,理解Huffman树的原理和应用场景,能够根据给定的字符频率构建最优的Huffman树,并生成相应的Huffman编码,提高对数据压缩等实际问题的解决能力。
- 通过对二叉树相关知识的学习和编程实践,加深对二叉树的理解,逐步培养运用二叉树结构解决实际问题的编程能力,提升算法设计、调试和分析的综合素养。
二,问题描述
编程实现二叉树的下列基本运算。
(1)创建一棵二叉树;
(2)求二叉树中结点的总数;
(3)统计二叉树的叶结点个数;
(4)求二叉树的深度;
(5)用按层次顺序遍历二叉树的方法,统计树中具有度为1的结点数目;
(6)交换二叉树每个结点的左孩子和右孩子;
(7)输出二叉树。
三,基本要求
(1)采用二叉链表作为二叉树结点的存储结构;
(2)设计实现上述各种运算的算法;
(3)设计主函数以完成对上述算法的调用,并输出结果;
(4)完善参考程序;
(5)设计测试数据,上机调试、测试完善后的参考程序,保存并打印测试结果,对算法性能进行分析。
四,实验操作
1,双击Visual Studio程序快捷图标,启动程序。

2,之前创建过项目的话,直接打开即可,这里选择【创建新项目】。

3,单击选择【空项目】——单击【下一步】按钮。
4,编辑好项目的名称和存放路径,然后单击【创建】按钮。

5,创建C++程序文件,右击【源文件】——选择【添加】——【新建项】。

6,输入项目名称,单击【添加】按钮。

7,编写代码,单击运行按钮,运行程序。

五,示例代码
#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>typedef struct BiTNode { // 定义二叉树的结点结构char data; // 假定树结点的元素类型为charstruct BiTNode* lchild; // 左指针struct BiTNode* rchild; // 右指针
} BiTNode, * BiTree;void CreateBiTree(BiTree& T)
{ // 先序递归遍历方式创建一棵二叉树char ch;scanf("\n%c", &ch); // 输入根结点的值if (ch == '#') // 终止项T = NULL;else{T = (BiTree)malloc(sizeof(BiTNode)); // 创建根结点if (!T)exit(-1);T->data = ch;printf("\n请输入%c结点的左子结点(#表无):", T->data); // 先序遍历创建左子树CreateBiTree(T->lchild);printf("\n请输入%c结点的右子结点(#表无):", T->data); // 先序遍历创建右子树CreateBiTree(T->rchild);}
}//统计二叉树的叶子结点个数。
int LeafNodeCount(BiTree T)
{if (T == NULL)return 0; //如果是空树,则叶子结点个数为0else if (T->lchild == NULL && T->rchild == NULL) // 判断该结点是否是叶子结点(左孩子右孩子都为空),若是则返回1return 1;elsereturn LeafNodeCount(T->lchild) + LeafNodeCount(T->rchild);
}//交换二叉树每个结点的左孩子和右孩子。
void ChangeLR(BiTree T)
{BiTree p;if (T == NULL || (T->lchild == NULL && T->rchild == NULL))return;else{p = T->lchild;T->lchild = T->rchild;T->rchild = p;}ChangeLR(T->lchild);ChangeLR(T->rchild); // 交换右子树上结点的左右孩子
}
// 统计二叉树中度为1的结点数
int D1_Nodes(BiTree T)
{int num1, num2;if (T == NULL || (!T->lchild && !T->rchild))return 0;num1 = D1_Nodes(T->lchild);num2 = D1_Nodes(T->rchild);if (T->lchild && !T->rchild) // 若结点T的左子树非空,右子树空,则返回左// 子树上度为1的结点数加1(当前结点度为1)return num1 + 1;else if (!T->lchild && T->rchild)return num2 + 1;elsereturn num1 + num2;
}//求二叉树结点数目
int Nodes(BiTree T)
{int num1, num2;if (T == NULL)return 0;else {num1 = Nodes(T->lchild); // 统计左子树的结点数num2 = Nodes(T->rchild); // 统计右子树的结点数return num1 + num2 + 1; // 左右子树结点总数加1(当前结点)}
}// 求二叉树的深度
int BiTreeDepth(BiTree T)
{int leftdep, rightdep;if (T == NULL) // 终止项return 0;else{leftdep = BiTreeDepth(T->lchild);rightdep = BiTreeDepth(T->rchild);return (leftdep > rightdep) ? (leftdep + 1) : (rightdep + 1);}
}
//以括号表示格式输出二叉树
void OutputBiTree(BiTree T)
{ // 先序递归遍历方式输出括号表示的二叉树if (T != NULL) // 终止项{printf("%c", T->data); // 访问根结点if (T->lchild != NULL || T->rchild != NULL){printf("("); // 根的孩子用圆括号对括OutputBiTree(T->lchild); // 先序遍历输出左子树if (T->rchild != NULL)printf(","); // 根的左右孩子以“,”分隔OutputBiTree(T->rchild); // 先序遍历输出右子树printf(")"); // 根的孩子用圆括号对括}}
}void main()
{int n;BiTNode* proot; // 定义树proot = NULL; // 初始化为空树printf("请输入根结点元素(#表无):"); // 创建二叉树CreateBiTree(proot);printf("\n(1)二叉树创建成功!其括号表示格式输出:\n\t");OutputBiTree(proot);printf("\n");n = Nodes(proot);printf("(2)二叉树结点总数是:%d\n", n);n = LeafNodeCount(proot);printf("(3)二叉树的叶子结点数为:%d\n", n);n = BiTreeDepth(proot);printf("(4)二叉树的深度是:%d\n", n);n = D1_Nodes(proot);printf("(5)二叉树中度为1的结点数是:%d\n", n);ChangeLR(proot);printf("(6)交换所有结点的左右孩子后二叉树括号表示法输出:\n\t");OutputBiTree(proot);printf("\n");
}
六,运行效果
1,实验测试效果。

2,编写代码运行后的效果。

相关文章:

数据结构实验7.2:二叉树的基本运算
文章目录 一,实验目的二,问题描述三,基本要求四,实验操作五,示例代码六,运行效果 一,实验目的 深入理解树与二叉树的基本概念,包括节点、度、层次、深度等,清晰区分二叉…...
Go-zero框架修改模版进行handler统一响应封装
使用go-zero快速生成接口的时候,发现还是有一些情况不太好处理,比如说,想要自定义响应封装等等。 最开始第一版写api文件的时候,写法是这样的。 type LoginRequest {UserName string json:"userName"Password string …...

AI专题(一)----NLP2SQL探索以及解决方案
前面写了很多编码、算法、底层计算机原理等相关的技术专题,由于工作方向调整的缘故,今天开始切入AI人工智能相关介绍。本来按照规划,应该先从大模型的原理开始介绍会比较合适,但是计划赶不上变化,前面通用大模型的工作…...

深入理解 React Hooks:简化状态管理与副作用处理
在现代前端开发中,React 已经成为了最受欢迎的 JavaScript 库之一。随着 React 16.8 的发布,React Hooks 的引入彻底改变了开发者编写组件的方式。Hooks 提供了一种更简洁、更直观的方式来管理组件的状态和副作用,使得函数组件能够拥有类组件…...

Spring Boot 实现防盗链
在 Spring Boot 项目中实现防盗链可以通过多种方式,下面为你介绍两种常见的实现方法,分别是基于请求头 Referer 和基于令牌(Token)的防盗链。 基于请求头 Referer 的防盗链 这种方法通过检查请求头中的 Referer 字段,…...

Java 动态代理实现
Java 动态代理实现 一、JDK动态代理二、CGLIB动态代理三、动态代理的应用场景四、JDK代理与CGLIB代理比较 动态代理是Java中一种强大的技术,它允许在运行时创建代理对象,用于拦截对目标对象的方法调用。 一、JDK动态代理 JDK动态代理是Java标准库提供的代…...
:6G技术加速落地 卫星通信网络迎来组网高潮)
2025年4月通信科技领域周报(4.07-4.13):6G技术加速落地 卫星通信网络迎来组网高潮
2025年4月通信科技领域周报(4.07-4.13):6G技术加速落地 卫星通信网络迎来组网高潮 目录 2025年4月通信科技领域周报(4.07-4.13):6G技术加速落地 卫星通信网络迎来组网高潮一、本周热点回顾1. 华为发布全球首…...

《手环表带保养全攻略:材质、清洁与化学品避坑指南》
系列文章目录 文章目录 系列文章目录前言一、表带材质特性与专属养护方案二、清洁剂使用红黑榜三、家庭清洁实验:化学反应警示录四、保养实践方法论总结 前言 手环作为现代生活的智能伴侣,表带材质选择丰富多样。从柔软亲肤的皮质到耐用耐磨的金属&…...

人脸扫描黑科技:多相机人脸扫描设备,打造你的专属数字分身
随着科技的迅猛发展,人脸扫描这个词已经并不陌生,通过人脸扫描设备制作超写实人脸可以为影视制作打造逼真角色、提升游戏沉浸感,还能助力教育机构等领域生产数字人以丰富教学资源,还在安防、身份识别等领域发挥关键作用࿰…...

基于Python的中国象棋小游戏的设计与实现
基于Python的中国象棋小游戏的设计与实现 第一章 绪论1.1 研究背景1.2 研究意义 第二章 需求分析2.1 需求分析2.1.1核心功能需求2.1.2 用户体验需求2.1.3 衍生功能需求 2.2 可行性分析2.2.1 技术可行性2.2.2 经济可行性2.2.3 市场可行性2.2.4 法律与合规性 第三章 概要设计3.1 …...

简单好用的在线工具
用AI写了一些在线工具,简介好用,推荐给大家,欢迎大家使用并提议意见。 网址:https://www.bittygarden.com/ 目前已有以下功能: MD5SM3SHAUnicode 编码Unicode 解码Base32 编码Base32 解码Base64 编码Base64 解码URL …...
适配器模式)
JAVA设计模式——(1)适配器模式
JAVA设计模式——(1)适配器模式 目的理解实现优势 目的 将一个类的接口变换成客户端所期待的另一种接口,从而使原本因接口不匹配而无法一起工作的两个类能够在一起工作。 理解 可以想象成一个国标的插头,结果插座是德标的&…...

外卖市场规模巨大,是宽广赛道?京东CEO发言
大家好,我是小悟。 在竞争激烈的外卖市场中,京东作为新入局者,正以独特的战略视角和坚定的决心,重新定义外卖行业的竞争格局。 近日,京东集团CEO许冉在接受采访时表示:“外卖行业本就是一个宽广的赛道&am…...
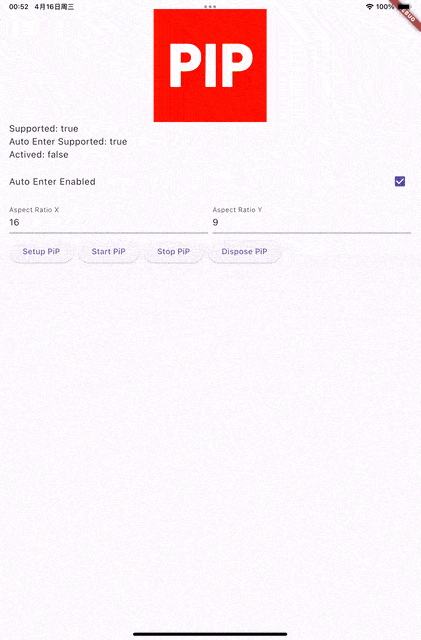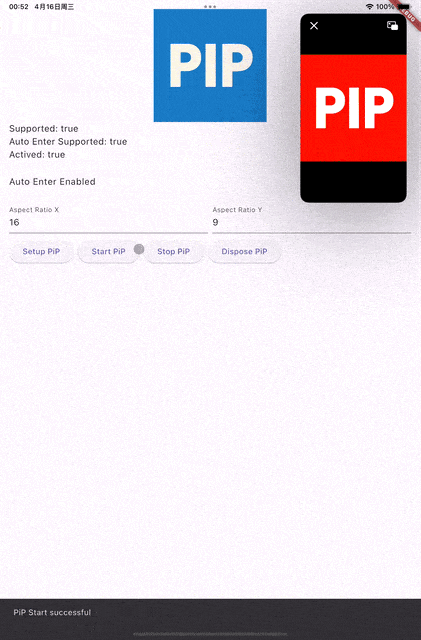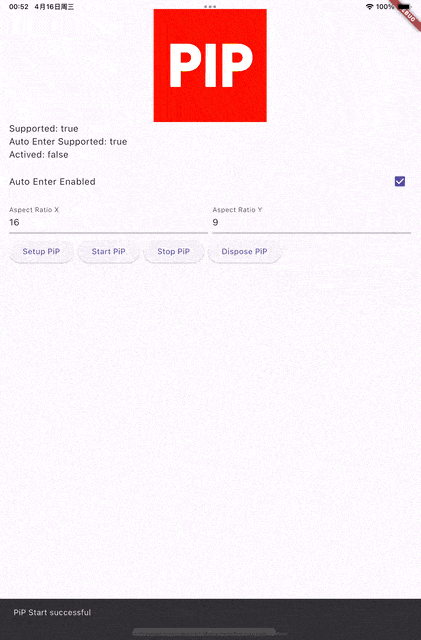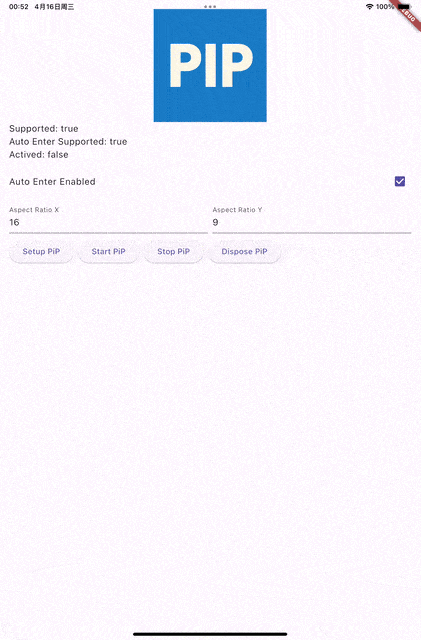
Flutter PIP 插件 ---- iOS Video Call 自定义PIP WINDOW渲染内容
简介 画中画(Picture in Picture, PiP)是一项允许用户在使用其他应用时继续观看视频内容的功能。本文将详细介绍如何在 iOS 应用中实现 PiP 功能,包括自定义内容渲染和控制系统控件的显示。 效果展示 功能特性 已完成功能 ✅ 基础 PiP 接口实现(设置…...
 的完整说明)
TensorFlow 实现 Mixture Density Network (MDN) 的完整说明
本文档详细解释了一段使用 TensorFlow 构建和训练混合密度网络(Mixture Density Network, MDN)的代码,涵盖数据生成、模型构建、自定义损失函数与预测可视化等各个环节。 1. 导入库与设置超参数 import numpy as np import tensorflow as t…...

xml+html 概述
1.什么是xml xml 是可扩展标记语言的缩写: Extensible Markup Language。 <root><h1> text 1</h1> </root> web 应用开发,需要配置 web.xml,就是个典型的 xml文件 <web-app><servlet><servlet-name&…...

混合精度训练中的算力浪费分析:FP16/FP8/BF16的隐藏成本
在大模型训练场景中,混合精度训练已成为降低显存占用的标准方案。然而,通过NVIDIA Nsight Compute深度剖析发现,精度转换的隐藏成本可能使理论算力利用率下降40%以上。本文基于真实硬件测试数据,揭示不同精度格式的计算陷阱。…...

Python语法系列博客 · 第5期[特殊字符] 模块与包的导入:构建更大的程序结构
上一期小练习解答(第4期回顾) ✅ 练习1:判断偶数函数 def is_even(num):return num % 2 0print(is_even(4)) # True print(is_even(5)) # False✅ 练习2:求平均值 def avg(*scores):return sum(scores) / len(scores)print(…...

Sleuth+Zipkin 服务链路追踪
微服务架构中,为了更好追踪服务之间调用,实现时间分析,性能瓶颈分析,故障排查,因此有必要搭建链路追踪。下面简单介绍下实现的过程。 一.引入依赖 <!-- 链路追踪 zipkin已经集成有sleuth,不需要再单独…...
)
意志力的源头——AMCC(前部中扣带皮层)
AMCC(前部中扣带皮层)在面对痛苦需要坚持的事情时会被激活。它的存在能够使人类个体在面临困难的事、本能感到不愿意的麻烦事情时,能够自愿地去做这些事——这些事必须是局部痛苦或宏观的痛苦,即微小的痛苦micro-sucks。 AMCC更多…...

[Jenkins]pnpm install ‘pnpm‘ 不是内部或外部命令,也不是可运行的程序或批处理文件。
这个错误提示再次说明:你的系统(CMD 或 Jenkins 环境)找不到 pnpm 命令的位置。虽然你可能已经用 npm install -g pnpm 安装过,但系统不知道它装在哪里,也就无法执行 pnpm 命令。 ✅ 快速解决方法:直接用完…...

Java从入门到“放弃”(精通)之旅——数组的定义与使用⑥
Java从入门到“放弃”(精通)之旅🚀——数组⑥ 前言——什么是数组? 数组:可以看成是相同类型元素的一个集合,在内存中是一段连续的空间。比如现实中的车库,在java中,包含6个整形类…...

部署rocketmq集群
容器化部署RocketMQ5.3.1集群 背景: 生产环境单机的MQ不具有高可用,所以我们应该部署成集群模式,这里给大家部署一个双主双从异步复制的Broker集群 一、安装docker yum install -y docker systemctl enable docker --now # 单机部署参考: https://www.cnblogs.com/hsyw/p/1…...

如何对docker镜像存在的gosu安全漏洞进行修复——筑梦之路
这里以mysql的官方镜像为例进行说明,主要流程为: 1. 分析镜像存在的安全漏洞具体是什么 2. 根据分析结果有针对性地进行修复处理 3. 基于当前镜像进行修复安全漏洞并复核验证 # 镜像地址mysql:8.0.42 安全漏洞现状分析 dockerhub网站上获取该镜像的…...

Ubuntu 安装WPS Office
文章目录 Ubuntu 安装WPS Office下载安装文件安装WPS问题1.下载缺失字体文件2.安装缺失字体 Ubuntu 安装WPS Office 下载安装文件 需要到 WPS官网 下载最新软件,比如wps-office_12.1.0.17900_amd64.deb 安装WPS 执行命令进行安装 sudo dpkg -i wps-office_12.1…...

基于springboot的老年医疗保健系统
博主介绍:java高级开发,从事互联网行业六年,熟悉各种主流语言,精通java、python、php、爬虫、web开发,已经做了六年的毕业设计程序开发,开发过上千套毕业设计程序,没有什么华丽的语言࿰…...

使用Ollama本地运行deepseek模型
Ollama 是一个用于管理 AI 模型的工具 下载 Ollama Ollama 选择版本 下载模型 安装好后,下载模型 选择模型 选择模型大小,复制对应命令(越大越聪明,但是内存要求越高) 打开控制台运行命令,第一次运行会自动…...

网络编程 - 3
目录 UDP 连接拓展(业务逻辑) 词典服务器实现 完 UDP 连接拓展(业务逻辑) 我们上一篇文章实现了一个回显服务器,在服务端中业务方法 process 中,只是单纯的将客户端输入的东西 return 了一下࿰…...

rebase和merge的区别
目录 1. 合并机制与提交历史 2. 冲突处理方式 3. 历史追溯与团队协作 4. 推荐实践 5. 撤销难度 git rebase和git merge是Git中两种不同的分支合并策略,核心区别在于提交历史的处理方式:merge保留原始分支结构并生成合并提交&am…...

5G 毫米波滤波器的最优选择是什么?
新的选择有很多,但到目前为止还没有明确的赢家。 蜂窝电话技术利用大量的带带,为移动用途提供不断增加的带宽。 其中的每一个频带都需要透过滤波器将信号与其他频带分开,但目前用于手机的滤波器技术可能无法扩展到5G所规划的全部毫米波&#…...
