LeetCode：DFS综合练习

简单

1863. 找出所有子集的异或总和再求和

一个数组的 异或总和 定义为数组中所有元素按位 XOR 的结果；如果数组为 空 ，则异或总和为 0 。

• 例如，数组 [2,5,6] 的 异或总和 为 2 XOR 5 XOR 6 = 1 。

给你一个数组 nums ，请你求出 nums 中每个 子集 的 异或总和 ，计算并返回这些值相加之 和 。

**注意：**在本题中，元素 相同 的不同子集应 多次 计数。

数组 a 是数组 b 的一个 子集 的前提条件是：从 b 删除几个（也可能不删除）元素能够得到 a 。

示例 1：

输入：nums = [1,3]
输出：6
解释：[1,3] 共有 4 个子集：
- 空子集的异或总和是 0 。
- [1] 的异或总和为 1 。
- [3] 的异或总和为 3 。
- [1,3] 的异或总和为 1 XOR 3 = 2 。
0 + 1 + 3 + 2 = 6

示例 2：

输入：nums = [5,1,6]
输出：28
解释：[5,1,6] 共有 8 个子集：
- 空子集的异或总和是 0 。
- [5] 的异或总和为 5 。
- [1] 的异或总和为 1 。
- [6] 的异或总和为 6 。
- [5,1] 的异或总和为 5 XOR 1 = 4 。
- [5,6] 的异或总和为 5 XOR 6 = 3 。
- [1,6] 的异或总和为 1 XOR 6 = 7 。
- [5,1,6] 的异或总和为 5 XOR 1 XOR 6 = 2 。
0 + 5 + 1 + 6 + 4 + 3 + 7 + 2 = 28

示例 3：

输入：nums = [3,4,5,6,7,8]
输出：480
解释：每个子集的全部异或总和值之和为 480 。

提示：

• 1 <= nums.length <= 12
• 1 <= nums[i] <= 20

int ans = 0;
int path = 0;int subsetXORSum(vector<int>& nums) {dfs(nums, 0);return ans;
}void dfs(vector<int>& nums, int pos) {ans += path;for (int i = pos; i < nums.size(); ++i) {path ^= nums[i];dfs(nums, i + 1);path ^= nums[i];}
}

面试题 08.06. 汉诺塔问题

在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。

请编写程序，用栈将所有盘子从第一根柱子移到最后一根柱子。

你需要原地修改栈。

示例 1：

 输入：A = [2, 1, 0], B = [], C = []输出：C = [2, 1, 0]

示例 2：

 输入：A = [1, 0], B = [], C = []输出：C = [1, 0]

提示：

1. A 中盘子的数目不大于 14 个。

void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {move(A, B, C, A.size());
}void move(vector<int>& A, vector<int>& B, vector<int>& C, int n) {if (n == 1) {C.push_back(A.back());A.pop_back();return;}move(A, C, B, n - 1); // 将A上的n-1个借助C移到B上C.push_back(A.back());A.pop_back();move(B, A, C, n - 1); // 将B上的n-1个借助A移到C上
}

中等

17. 电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

输入：digits = ""
输出：[]

示例 3：

输入：digits = "2"
输出：["a","b","c"]

提示：

• 0 <= digits.length <= 4
• digits[i] 是范围 ['2', '9'] 的一个数字。

vector<string> ans;
string path;
vector<string> nums = {"", "", "abc", "def","ghi", "jkl", "mno","pqrs", "tuv", "wxyz"
};vector<string> letterCombinations(string digits) {if (digits.size() == 0) {return ans;}dfs(digits, 0);return ans;
}void dfs(string digits, int pos) {if (path.size() == digits.size()) {ans.push_back(path);return;}int n = digits[pos] - '0';string str = nums[n];for (int i = 0; i < str.size(); ++i) {path.push_back(str[i]);dfs(digits, pos + 1);path.pop_back();}
}

22. 括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

示例 2：

输入：n = 1
输出：["()"]

提示：

• 1 <= n <= 8

vector<string> ans;
string path;vector<string> generateParenthesis(int n) {dfs(n, 0, 0);return ans;
}void dfs(int n, int left, int right) {if (left + right == 2 * n) {ans.push_back(path);return;}if (left < n) {path.push_back('(');dfs(n, left + 1, right);path.pop_back();}if (right < left) {path.push_back(')');dfs(n, left, right + 1);path.pop_back();}
}

39. 组合总和

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

提示：

• 1 <= candidates.length <= 30
• 2 <= candidates[i] <= 40
• candidates 的所有元素 互不相同
• 1 <= target <= 40

vector<vector<int>> ans;
vector<int> path;vector<vector<int>> combinationSum(vector<int>& candidates, int target) {dfs(candidates, target, 0, 0);return ans;
}void dfs(vector<int>& candidates, int target, int sum, int pos) {if (sum > target) {return;}if (sum == target) {ans.push_back(path);return;}for (int i = pos; i < candidates.size(); ++i) {path.push_back(candidates[i]);dfs(candidates, target, sum + candidates[i], i);path.pop_back();}
}

46. 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

• 1 <= nums.length <= 6
• -10 <= nums[i] <= 10
• nums 中的所有整数 互不相同

vector<vector<int>> ans;
vector<int> path;
vector<bool> vis;vector<vector<int>> permute(vector<int>& nums) {int n = nums.size();vis = vector<bool>(n, false);dfs(nums);return ans;
}void dfs(vector<int>& nums) {int n = nums.size();if (path.size() == n) {ans.push_back(path);return;}for (int i = 0; i < n; ++i) {if (vis[i] == false) {path.push_back(nums[i]);vis[i] = true;dfs(nums);path.pop_back();vis[i] = false;}}
}

47. 全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],[1,2,1],[2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

• 1 <= nums.length <= 8
• -10 <= nums[i] <= 10

vector<vector<int>> ans;
vector<int> path;
vector<bool> vis;vector<vector<int>> permuteUnique(vector<int>& nums) {sort(nums.begin(), nums.end());vis = vector<bool>(nums.size(), false);dfs(nums, 0);return ans;
}void dfs(vector<int>& nums, int pos) {if (path.size() == nums.size()) {ans.push_back(path);return;}for (int i = 0; i < nums.size(); ++i) {if (vis[i] == true || (i > 0 && nums[i - 1] == nums[i] && vis[i - 1] == true)) {continue;}path.push_back(nums[i]);vis[i] = true;dfs(nums, i + 1);vis[i] = false;path.pop_back();}
}

50. Pow(x, n)

实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，xn ）。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3
输出：9.26100

示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示：

• -100.0 < x < 100.0
• -2^31 <= n <= 2^31-1
• n 是一个整数
• 要么 x 不为零，要么 n > 0 。
• -10^4 <= x^n <= 10^4

double myPow(double x, int n) {return n >= 0 ? quickMul(x, n) : 1.0 / quickMul(x, -(long long)n);
}double quickMul(double x, long long n) {if (n == 0) {return 1.0;}double tmp = quickMul(x, n / 2);return (n % 2 ? tmp * tmp * x : tmp * tmp);
}

77. 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[[2,4],[3,4],[2,3],[1,2],[1,3],[1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

• 1 <= n <= 20
• 1 <= k <= n

vector<vector<int>> ans;
vector<int> path;vector<vector<int>> combine(int n, int k) {dfs(n, k, 1);return ans;
}void dfs(int n, int k, int pos) {if (path.size() == k) {ans.push_back(path);return;}for (int i = pos; i <= n; ++i) {path.push_back(i);dfs(n, k, i + 1);path.pop_back();}
}

78. 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

• 1 <= nums.length <= 10
• -10 <= nums[i] <= 10
• nums 中的所有元素 互不相同

vector<vector<int>> ans;
vector<int> path;vector<vector<int>> subsets(vector<int>& nums) {dfs(nums, 0);return ans;
}void dfs(vector<int>& nums, int pos) {if (pos == nums.size()) {ans.push_back(path);return;}dfs(nums, pos + 1);path.push_back(nums[pos]);dfs(nums, pos + 1);path.pop_back();
}

另一种方法

vector<vector<int>> ans;
vector<int> path;vector<vector<int>> subsets(vector<int>& nums) {dfs(nums, 0);return ans;
}void dfs(vector<int>& nums, int pos) {ans.push_back(path);for (int i = pos; i < nums.size(); ++i) {path.push_back(nums[i]);dfs(nums, i + 1);path.pop_back();}
}

79. 单词搜索

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例 1：

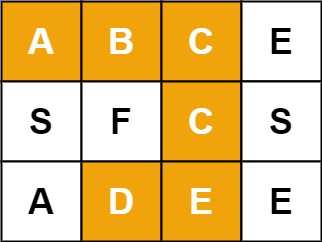
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2：

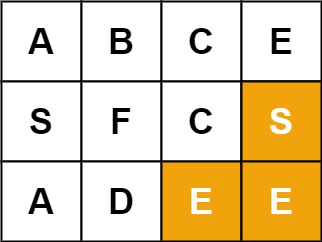
输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE"
输出：true

示例 3：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB"
输出：false

提示：

• m == board.length
• n = board[i].length
• 1 <= m, n <= 6
• 1 <= word.length <= 15
• board 和 word 仅由大小写英文字母组成

vector<vector<bool>> vis;
const int dx[4] = {0, 0, 1, -1};
const int dy[4] = {1, -1, 0, 0};bool exist(vector<vector<char>>& board, string word) {int n = board.size(), m = board[0].size();vis = vector<vector<bool>>(n, vector<bool>(m, false));for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {if (board[i][j] == word[0]) {vis[i][j] = true;if (dfs(board, word, i, j, 1) == true) {return true;}vis[i][j] = false;}}}return false;
}bool dfs(vector<vector<char>>& board, const string& word, int x, int y, int pos) {if (pos == word.size()) {return true;}int n = board.size(), m = board[0].size();for (int k = 0; k < 4; ++k) {int nx = x + dx[k], ny = y + dy[k];if (nx >= 0 && nx < n && ny >= 0 && ny < m && board[nx][ny] == word[pos] && vis[nx][ny] == false) {vis[nx][ny] = true;if (dfs(board, word, nx, ny, pos + 1) == true) {return true;}vis[nx][ny] = false;}}return false;
}

494. 目标和

给你一个非负整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：

• 例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。

返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

示例 1：

输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

示例 2：

输入：nums = [1], target = 1
输出：1

提示：

• 1 <= nums.length <= 20
• 0 <= nums[i] <= 1000
• 0 <= sum(nums[i]) <= 1000
• -1000 <= target <= 1000

int ans = 0;int findTargetSumWays(vector<int>& nums, int target) {dfs(nums, target, 0, 0);return ans;
}void dfs(vector<int>& nums, int target, int pos, int sum) {if (pos == nums.size()) {if (target == sum) {ans++;}return;}dfs(nums, target, pos + 1, sum + nums[pos]);dfs(nums, target, pos + 1, sum - nums[pos]);
}

526. 优美的排列

假设有从 1 到 n 的 n 个整数。用这些整数构造一个数组 perm（下标从 1 开始），只要满足下述条件 之一 ，该数组就是一个 优美的排列 ：

• perm[i] 能够被 i 整除
• i 能够被 perm[i] 整除

给你一个整数 n ，返回可以构造的 优美排列 的 数量 。

示例 1：

输入：n = 2
输出：2
解释：
第 1 个优美的排列是 [1,2]：- perm[1] = 1 能被 i = 1 整除- perm[2] = 2 能被 i = 2 整除
第 2 个优美的排列是 [2,1]:- perm[1] = 2 能被 i = 1 整除- i = 2 能被 perm[2] = 1 整除

示例 2：

输入：n = 1
输出：1

提示：

• 1 <= n <= 15

int ans;
vector<bool> vis;int countArrangement(int n) {vis = vector<bool>(n, false);dfs(n, 1);return ans;
}void dfs(int n, int pos) {if (pos == n + 1) {ans++;return;}for (int i = 1; i <= n; ++i) {if (vis[i] == false && (i % pos == 0 || pos % i == 0)) {vis[i] = true;dfs(n, pos + 1);vis[i] = false;}}
}

784. 字母大小写全排列

给定一个字符串 s ，通过将字符串 s 中的每个字母转变大小写，我们可以获得一个新的字符串。

返回 所有可能得到的字符串集合 。以 任意顺序 返回输出。

示例 1：

输入：s = "a1b2"
输出：["a1b2", "a1B2", "A1b2", "A1B2"]

示例 2:

输入: s = "3z4"
输出: ["3z4","3Z4"]

提示:

• 1 <= s.length <= 12
• s 由小写英文字母、大写英文字母和数字组成

vector<string> ans;vector<string> letterCasePermutation(string s) {dfs(s, 0);return ans;
}void dfs(string s, int pos) {if (pos == s.size()) {ans.push_back(s);return;}if (isdigit(s[pos])) {dfs(s, pos + 1);} else {s[pos] = tolower(s[pos]);dfs(s, pos + 1);s[pos] = toupper(s[pos]);dfs(s, pos + 1);}
}

1219. 黄金矿工

你要开发一座金矿，地质勘测学家已经探明了这座金矿中的资源分布，并用大小为 m * n 的网格 grid 进行了标注。每个单元格中的整数就表示这一单元格中的黄金数量；如果该单元格是空的，那么就是 0。

为了使收益最大化，矿工需要按以下规则来开采黄金：

• 每当矿工进入一个单元，就会收集该单元格中的所有黄金。
• 矿工每次可以从当前位置向上下左右四个方向走。
• 每个单元格只能被开采（进入）一次。
• 不得开采（进入）黄金数目为 0 的单元格。
• 矿工可以从网格中 任意一个 有黄金的单元格出发或者是停止。

示例 1：

输入：grid = [[0,6,0],[5,8,7],[0,9,0]]
输出：24
解释：
[[0,6,0],[5,8,7],[0,9,0]]
一种收集最多黄金的路线是：9 -> 8 -> 7。

示例 2：

输入：grid = [[1,0,7],[2,0,6],[3,4,5],[0,3,0],[9,0,20]]
输出：28
解释：
[[1,0,7],[2,0,6],[3,4,5],[0,3,0],[9,0,20]]
一种收集最多黄金的路线是：1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7。

提示：

• 1 <= grid.length, grid[i].length <= 15
• 0 <= grid[i][j] <= 100
• 最多 25 个单元格中有黄金。

int ans = 0, path = 0;
vector<vector<bool>> vis;
const int dx[4] = {0, 0, 1, -1};
const int dy[4] = {1, -1, 0, 0};int getMaximumGold(vector<vector<int>>& grid) {int n = grid.size(), m = grid[0].size();vis = vector<vector<bool>>(n, vector<bool>(m, false));for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {if (grid[i][j] != 0) {dfs(grid, i, j);}}}return ans;
}void dfs(vector<vector<int>>& grid, int x, int y) {path += grid[x][y];vis[x][y] = true;ans = max(ans, path);int n = grid.size(), m = grid[0].size();for (int k = 0; k < 4; ++k) {int nx = x + dx[k], ny = y + dy[k];if (nx >= 0 && nx < n && ny >= 0 && ny < m && grid[nx][ny] != 0 && vis[nx][ny] == false) {dfs(grid, nx, ny);}}path -= grid[x][y];vis[x][y] = false;
}

困难

37. 解数独

编写一个程序，通过填充空格来解决数独问题。

数独的解法需 遵循如下规则：

1. 数字 1-9 在每一行只能出现一次。
2. 数字 1-9 在每一列只能出现一次。
3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

数独部分空格内已填入了数字，空白格用 '.' 表示。

示例 1：

输入：board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]]
输出：[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]]
解释：输入的数独如上图所示，唯一有效的解决方案如下所示：

提示：

• board.length == 9
• board[i].length == 9
• board[i][j] 是一位数字或者 '.'
• 题目数据 保证 输入数独仅有一个解

bool row[10][10], col[10][10], grid[3][3][10];void solveSudoku(vector<vector<char>>& board) {for (int i = 0; i < 9; ++i) {for (int j = 0; j < 9; ++j) {if (board[i][j] != '.') {int num = board[i][j] - '0';row[i][num] = col[j][num] = grid[i/3][j/3][num] = true;}}}dfs(board);
}bool dfs(vector<vector<char>>& board) {for (int i = 0; i < 9; ++i) {for (int j = 0; j < 9; ++j) {if (board[i][j] == '.') {for (int num = 1; num < 10; ++num) {if (!row[i][num] && !col[j][num] && !grid[i/3][j/3][num]) {board[i][j] = num + '0';row[i][num] = col[j][num] = grid[i/3][j/3][num] = true;if (dfs(board) == true)return true; board[i][j] = '.';row[i][num] = col[j][num] = grid[i/3][j/3][num] = false;}}return false;}}}return true;
}

51. N 皇后

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

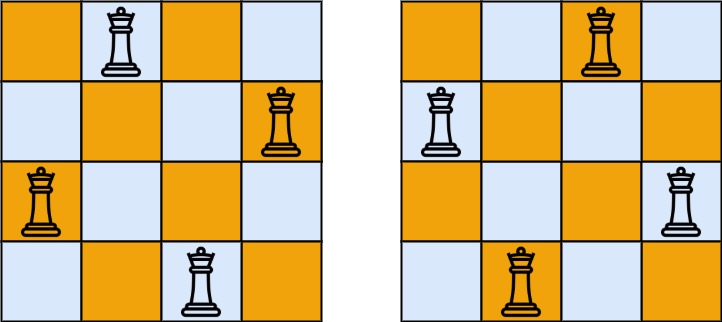
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

提示：

• 1 <= n <= 9

通过x = 0时y = b来判断是否当前斜线上有无皇后。

vector<vector<string>> ans;
vector<string> path;
bool vis[10];
bool vis1[20]; // y - x = b
bool vis2[20]; // y + x = bvector<vector<string>> solveNQueens(int n) {path.resize(n);for (int i = 0; i < n; ++i) {path[i].append(n, '.');}dfs(n, 0);return ans;
}void dfs(int n, int y) {if (y == n) {ans.push_back(path);return;}for (int x = 0; x < n; ++x) {if (!vis[x] && !vis1[y - x + 10] && !vis2[y + x]) {path[y][x] = 'Q';vis[x] = vis1[y - x + 10] = vis2[y + x] = true;dfs(n, y + 1);path[y][x] = '.';vis[x] = vis1[y - x + 10] = vis2[y + x] = false;}}
}

980. 不同路径 III

在二维网格 grid 上，有 4 种类型的方格：

• 1 表示起始方格。且只有一个起始方格。
• 2 表示结束方格，且只有一个结束方格。
• 0 表示我们可以走过的空方格。
• -1 表示我们无法跨越的障碍。

返回在四个方向（上、下、左、右）上行走时，从起始方格到结束方格的不同路径的数目**。**

每一个无障碍方格都要通过一次，但是一条路径中不能重复通过同一个方格。

示例 1：

输入：[[1,0,0,0],[0,0,0,0],[0,0,2,-1]]
输出：2
解释：我们有以下两条路径：
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2)
2. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2)

示例 2：

输入：[[1,0,0,0],[0,0,0,0],[0,0,0,2]]
输出：4
解释：我们有以下四条路径： 
1. (0,0),(0,1),(0,2),(0,3),(1,3),(1,2),(1,1),(1,0),(2,0),(2,1),(2,2),(2,3)
2. (0,0),(0,1),(1,1),(1,0),(2,0),(2,1),(2,2),(1,2),(0,2),(0,3),(1,3),(2,3)
3. (0,0),(1,0),(2,0),(2,1),(2,2),(1,2),(1,1),(0,1),(0,2),(0,3),(1,3),(2,3)
4. (0,0),(1,0),(2,0),(2,1),(1,1),(0,1),(0,2),(0,3),(1,3),(1,2),(2,2),(2,3)

示例 3：

输入：[[0,1],[2,0]]
输出：0
解释：
没有一条路能完全穿过每一个空的方格一次。
请注意，起始和结束方格可以位于网格中的任意位置。

提示：

• 1 <= grid.length * grid[0].length <= 20

int ans = 0, sum = 0; // sum 0的个数
vector<vector<bool>> vis;
const int dx[4] = {0, 0, -1, 1};
const int dy[4] = {1, -1, 0, 0};int uniquePathsIII(vector<vector<int>>& grid) {int n = grid.size(), m = grid[0].size();vis = vector<vector<bool>> (n, vector<bool>(m, false));int x, y;for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {if (grid[i][j] == 1) {vis[i][j] = true;x = i, y = j;} else if (grid[i][j] == 0) {sum++;}}}dfs(grid, x, y, 0);return ans;
}void dfs(vector<vector<int>>& grid, int x, int y, int cnt) {if (grid[x][y] == 2 && cnt == sum + 1) { // cnt 0+2 的个数ans++;return;}int n = grid.size(), m = grid[0].size();for (int k = 0; k < 4; ++k) {int nx = x + dx[k], ny = y + dy[k];if (nx >= 0 && nx < n && ny >= 0 && ny < m && grid[nx][ny] != -1 && vis[nx][ny] == false) {vis[nx][ny] = true;dfs(grid, nx, ny, cnt + 1);vis[nx][ny] = false;}}
}

1 <= grid.length * grid[0].length <= 20`

int ans = 0, sum = 0; // sum 0的个数
vector<vector<bool>> vis;
const int dx[4] = {0, 0, -1, 1};
const int dy[4] = {1, -1, 0, 0};int uniquePathsIII(vector<vector<int>>& grid) {int n = grid.size(), m = grid[0].size();vis = vector<vector<bool>> (n, vector<bool>(m, false));int x, y;for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {if (grid[i][j] == 1) {vis[i][j] = true;x = i, y = j;} else if (grid[i][j] == 0) {sum++;}}}dfs(grid, x, y, 0);return ans;
}void dfs(vector<vector<int>>& grid, int x, int y, int cnt) {if (grid[x][y] == 2 && cnt == sum + 1) { // cnt 0+2 的个数ans++;return;}int n = grid.size(), m = grid[0].size();for (int k = 0; k < 4; ++k) {int nx = x + dx[k], ny = y + dy[k];if (nx >= 0 && nx < n && ny >= 0 && ny < m && grid[nx][ny] != -1 && vis[nx][ny] == false) {vis[nx][ny] = true;dfs(grid, nx, ny, cnt + 1);vis[nx][ny] = false;}}
}