【基础算法】二分算法详解
🎯 前言:二分不是找某个数,而是找一个满足条件的位置/值
所以最关键的是:找到单调性,写好 check() 函数,剩下交给模板!
什么是二分算法
二分算法是一种在有序区间中查找答案的方法,时间复杂度:O(log n)。核心思想是:
- 每次把搜索区间分成两半,只保留可能存在答案的那一半,直到找到目标或搜索区间为空。
二分算法的种类
常见的二分算法就只有两种:
- 经典二分 (二分搜索)
- 二分答案 (二分答案 + check)
使用二分的特征 && 使用二分的条件
✨有序就能二分,单调就能逼近 (总结这一块,爆爆的)
使用二分的条件
使用二分需要问题的解具有“二段性”(True/False分界):
若某个值满足条件,则所有更大的值也满足(或反之)
这时就可以用二分在这个“分界点”上逼近最优解。
这个二段性可以理解成单调性,也就是可以将结果以目标值为界限分割成两段,一段大于等于target,另一段小于target;或者一段大于target,另一段小于等于target。具体根据题目要求来规划。
使用二分的特征
如何判断一个问题是否需要二分算法来解决,这也是初学者最关心的问题。
- 查找某个数是否存在
- 查找第一个/最后一个符合条件的位置
- 在问题的答案具有“二段性”时,搜索最优解
这类题目通常是求:最小值、最大值、最短时间、最小代价……
而且我们不难发现,这类问题的某些条件之间是有相互制约的线性关系的,比如某个变量随另一个变量的增长而增长,
于是在这道题的“解空间”中,整道题的答案序列是具有“二段性”的。
二分模板
二分查找 符合条件的区间 的左端点(起始位置)
给出条件:整个序列长度为 n (1-based序列)。
二段性体现:整个序列被分为 >= t 和 < t 两部分。
要查找 >= t 的最小值,也就是查找 >= t 区间的左端点。
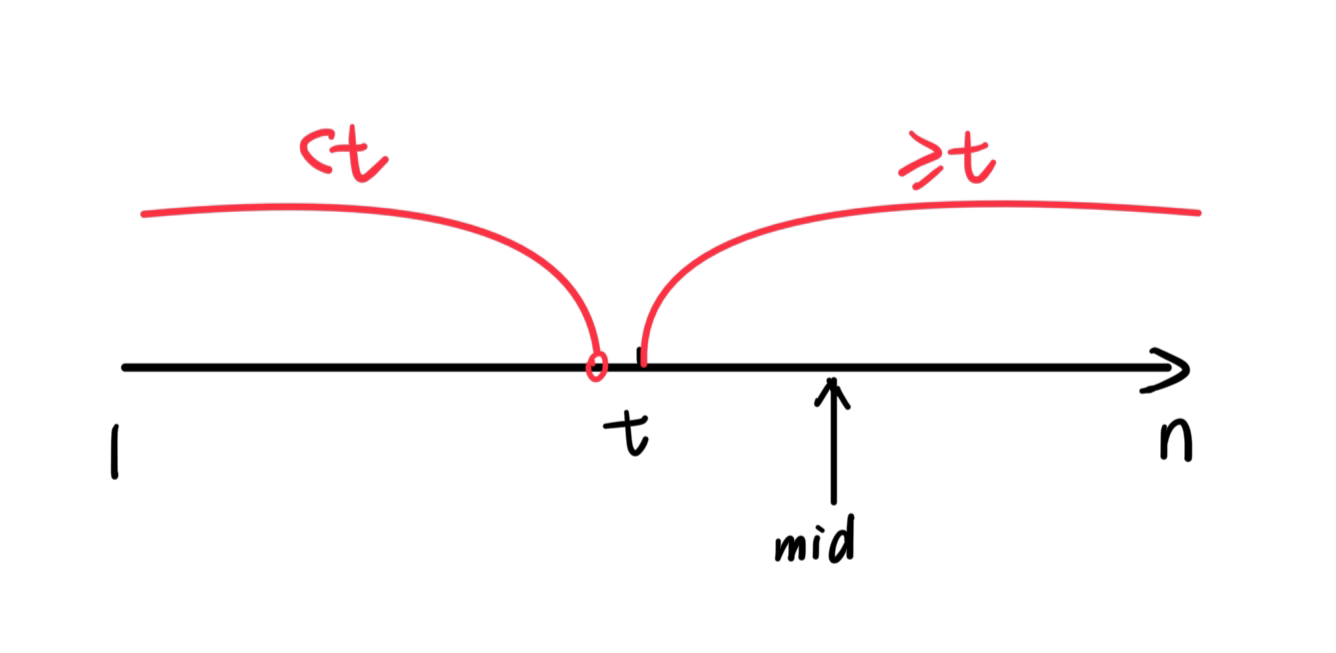
整个查找过程是怎样的呢?先根据 l 和 r 求出中间值 mid,判断 mid 和 t 的大小关系(二分答案就是通过 check 函数去判断 mid 所指向的位置在线性关系中的值与 t 的大小关系)
- 如果 >= t 那么 mid (二分答案就是 check(mid) ) 就落在 >= t 的区间上,下一步就是调整 r 的位置,缩小范围进一步查找。因为此时 mid 指向的位置可能是结果,所以就将 r 调整到 mid 的位置。
- 如果 < t 那么 mid (二分答案就是 check(mid) ) 就落在 < t 的区间上,下一步就是调整 l 的位置,缩小范围进一步查找。此时 mid 指向的位置不可能是结果,因为 < t 区间是取不到 t 的,所以即使 l 在及其靠近 t 的位置,也取不到 t ,那么我们就可以将 l 更新到 mid + 1 的位置。 mid + 1 的位置有可能是结果。
int l = 1, r = n;
while(l < r)
{int mid = (l + r) / 2;if(check(mid)) r = mid;else l = mid + 1;
}
//二分结束之后还需要判断结果是否存在,如果存在,二分停下的位置就是结果
二分查找 符合条件的区间 的右端点(终止位置)
查找中止位置,要找的就是 <= t 的区间的右端点
注意!!!找右端点时要注意求中间值是要+1的
小窍门:也可以先分析出l、r是怎么更新的,然后看l、r的更新有没有出现 -1,如果出现了 -1,求中间值时就要 +1 中和一下。
int l = 1, r = n;
while(l < r)
{int mid = (l + r + 1) / 2; //注意这里求中间值是要+1的if(check(mid)) l = mid;else r = mid - 1;
}
//别忘了判断结果
二分细节处理
细节部分想知道为什么会进入死循环的自己举个简单的例子画图理解就能明白了。我懒得画了。。。
求中间值
对于中间值 mid 的计算方式是有两种的:
int mid = (l + r) / 2;当序列个数是偶数个时,得到中点位于中间偏左;奇数个均相同。int mid = (l + r + 1) / 2;当序列个数是偶数个时,得到中点位于中间偏右
在找起始位置的时候,求中间值要用方式1,用方式2会死循环。
在找中止位置的时候,求中间值要用方式2,用方式1会死循环。
求中间值防溢出写法
int mid = l + (r - l) / 2;中间偏左int mid = l + (r - l + 1) / 2;中间偏右
循环条件
对于循环条件,无论是求起始位置还是求中止位置,统一要使用while(l < r),而不能写成while(l <= r),这样会死循环。
二分答案
通过题目来理解二分答案
P2440 木材加工
洛谷:P2440 木材加工

分析
这道题目难的在于思路,我们根据题意可得:木头切割的段数 k 和每段小木头的长度 l 是存在反比关系的。题目要求没小段木头的长度越大越好,并且要求出最大的长度,但是题目同时又给出了需要得到小段木头的数量。那么此时,题目就变成了在解空间有“二段性”的性质下,求最大值的问题。那么这题就是很明显的二分答案。ps:你总不能是看到我二分答案的tag就知道这题要用二分答案吧🤡。
其实这题我刚开始看到想到的是直接从大到小枚举所有的长度,但是分析数据范围就知道,暴力枚举肯定是超时的。于是在此基础上我们就要想优化办法,于是才得到的二分方案。解题思路是有个分析过程的,从暴力到优化。
相关文章:

【基础算法】二分算法详解
🎯 前言:二分不是找某个数,而是找一个满足条件的位置/值 所以最关键的是:找到单调性,写好 check() 函数,剩下交给模板! 什么是二分算法 二分算法是一种在有序区间中查找答案的方法,时间复杂度:O(log n)。核心思想是: 每次把搜索区间分成两半,只保留可能存在答案的…...

mysql——基础知识
关键字大小写不敏感 查看表结构中的 desc describe 描述 降序中的 desc descend 1. 数据库的操作 1. 创建数据库 create database 数据库名;为防止创建的数据库重复 CREATE DATABASE IF NOT EXISTS 数据库名;手动设置数据库采用的字符集 character set 字符集名;chars…...

html+js+clickhouse环境搭建
实验背景: 我目前有一台服务器A,和一台主机B,两台设备属于同一局域网,相互之间可以通讯。服务器A中部署着clickhouse,我在主机B中想直接通过javascript代码访问服务器中的clickhouse数据库并获取数据。 ClickHouse 服务…...

JWT算法详解
JWT(JSON Web Token)的整个算法流程主要基于其签名算法。以最常见的签名算法HS256(HMAC SHA256)为例,以下是详细的算法流程,涵盖编码、签名和验证过程: 编码 构造头部(Header&#x…...

OOA-CNN-LSTM-Attention、CNN-LSTM-Attention、OOA-CNN-LSTM、CNN-LSTM四模型多变量时序预测一键对比
OOA-CNN-LSTM-Attention、CNN-LSTM-Attention、OOA-CNN-LSTM、CNN-LSTM四模型多变量时序预测一键对比 目录 OOA-CNN-LSTM-Attention、CNN-LSTM-Attention、OOA-CNN-LSTM、CNN-LSTM四模型多变量时序预测一键对比预测效果基本介绍程序设计参考资料 预测效果 基本介绍 基于OOA-CN…...

Python Cookbook-6.6 在代理中托管特殊方法
任务 在新风格对象模型中,Python 操作其实是在类中查找特殊方法的(而不是在实例中那是经典对象模型的处理方式)。现在,需要将一些新风格的实例包装到代理类中,此代理可以选择将一些特殊方法委托给内部的被包装对象。 解决方案 你需要即时地…...

PCIE Spec ---Base Address Registers
7.5.1.2.1 Base Address Registers (Offset 10h - 24h) 在 boot 到操作系统之前,系统软件需要生产一个内存映射的 address map ,用于告诉系统有多少内存资源,以及相应功能需要的内存空间,所以在设备的 PCI 内存空间中就有了这个 …...
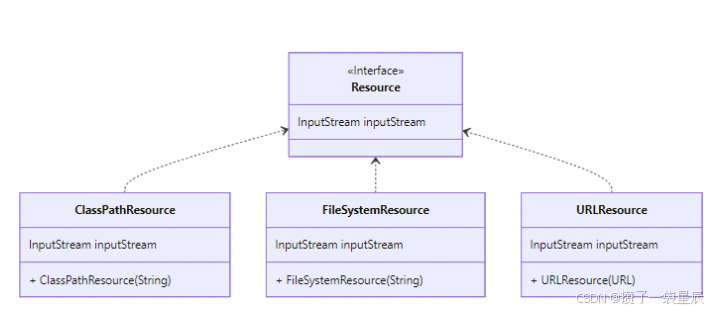
Spring如何通过XML注册Bean
在上一篇当中我们完成了对三种资源文件的读写 上篇内容:Spring是如何实现资源文件的加载 Test public void testClassPathResource() throws IOException { DefaultResourceLoader defaultResourceLoader new DefaultResourceLoader(); Resource resource …...

理解 `#pragma pack`:C/C++内存对齐的钥匙
引言:为什么我的网络程序收发的数据总是错位? 在网络编程中,你是否遇到过这样的困惑:明明发送方和接收方的结构体定义完全一样,但解析出来的数据却乱七八糟?这很可能是因为内存对齐在作祟。今天我们就来深…...

开源键鼠共享软件的“爱恨情仇“:Deskflow、InputLeap与Barrier的演化史
开源键鼠共享软件的"爱恨情仇":Deskflow、InputLeap与Barrier的演化史 一、血脉渊源:从Synergy到三足鼎立 这三款软件的起源都与 Synergy 这款商业软件密切相关: 2001年:Synergy开创软件化KVM先河2017年&…...

【Python核心库实战指南】从数据处理到Web开发
目录 前言:技术背景与价值当前技术痛点解决方案概述目标读者说明 一、技术原理剖析核心概念图解核心作用讲解关键技术模块对比 二、实战演示环境配置要求核心代码实现(5个案例)案例1:NumPy数组运算案例2:Pandas数据分析…...

运维:概念、模式与硬件基础
一、运维概述:从网管到智能运维的进化之路 1. 运维岗位的定义 IT运维管理是保障企业IT系统及网络可用性、安全性、稳定性,确保业务连续性的核心工作。通过专业技术手段,对计算机网络、应用系统、电信网络、软硬件环境及运维服务流程等进行综…...

基于Java的不固定长度字符集在指定宽度和自适应模型下图片绘制生成实战
目录 前言 一、需求介绍 1、指定宽度生成 2、指定列自适应生成 二、Java生成实现 1、公共方法 2、指定宽度生成 3、指定列自适应生成 三、总结 前言 在当今数字化与信息化飞速发展的时代,图像的生成与处理技术正日益成为众多领域关注的焦点。从创意设计到数…...

【版本控制】idea中使用git
大家好,我是jstart千语。接下来继续对git的内容进行讲解。也是在开发中最常使用,最重要的部分,在idea中操作git。目录在右侧哦。 如果需要git命令的详解: 【版本控制】git命令使用大全-CSDN博客 一、配置git 要先关闭项目…...
 在 VS2015 中正确关闭串口避免被占用)
QT:Qt5 串口模块 (QSerialPort) 在 VS2015 中正确关闭串口避免被占用
以下是使用 Qt5 串口模块 (QSerialPort) 在 VS2015 中正确关闭串口避免被占用的完整示例代码: #include <QSerialPort> #include <QDebug>// 创建全局或类成员变量(推荐使用智能指针) QSerialPort *serialPort nullptr; // 打开…...

Linux——入门常用基础指令
文章目录 Linux入门常用基础指令使用工具介绍基础指令clear指令pwd指令ls指令cd指令Linux系统下的文件路径及文件存储结构文件结构家目录绝对路径和相对路径tree工具 stat指令which指令alias指令touch指令mkdir指令cat指令rm指令man指令cp指令通配符 * Linux入门常用基础指令 …...

【技术追踪】Differential Transformer(ICLR-2025)
Differential Transformer:大语言模型新架构, 提出了 differential attention mechanism,Transformer 又多了一个小 trick~ 论文:Differential Transformer 代码:https://github.com/microsoft/unilm/tree/master/Diff…...

overlay 模块加载失败问题分析
问题背景 CentOS 7系统上,内核版本是3.10.0-693.21.1.el7.x86_64,加载overlay模块的时候失败了。错误提示说找不到支持的overlay文件系统,让我确认内核足够新并且已经加载了overlay支持。但是检查发现/lib/modules/3.10.0-693.el7.x86_64/ke…...

【Linux网络】应用层自定义协议与序列化
🌈个人主页:秦jh__https://blog.csdn.net/qinjh_?spm1010.2135.3001.5343 🔥 系列专栏:https://blog.csdn.net/qinjh_/category_12891150.html 目录 应用层 再谈 "协议" 网络版计算器 序列化 和 反序列化 重新理解…...

Vue接口平台学习十——接口用例页面2
效果图及简单说明 左边选择用例,右侧就显示该用例的详细信息。 使用el-collapse折叠组件,将请求到的用例详情数据展示到页面中。 所有数据内容,绑定到caseData中 // 页面绑定的用例编辑数据 const caseData reactive({title: "",…...
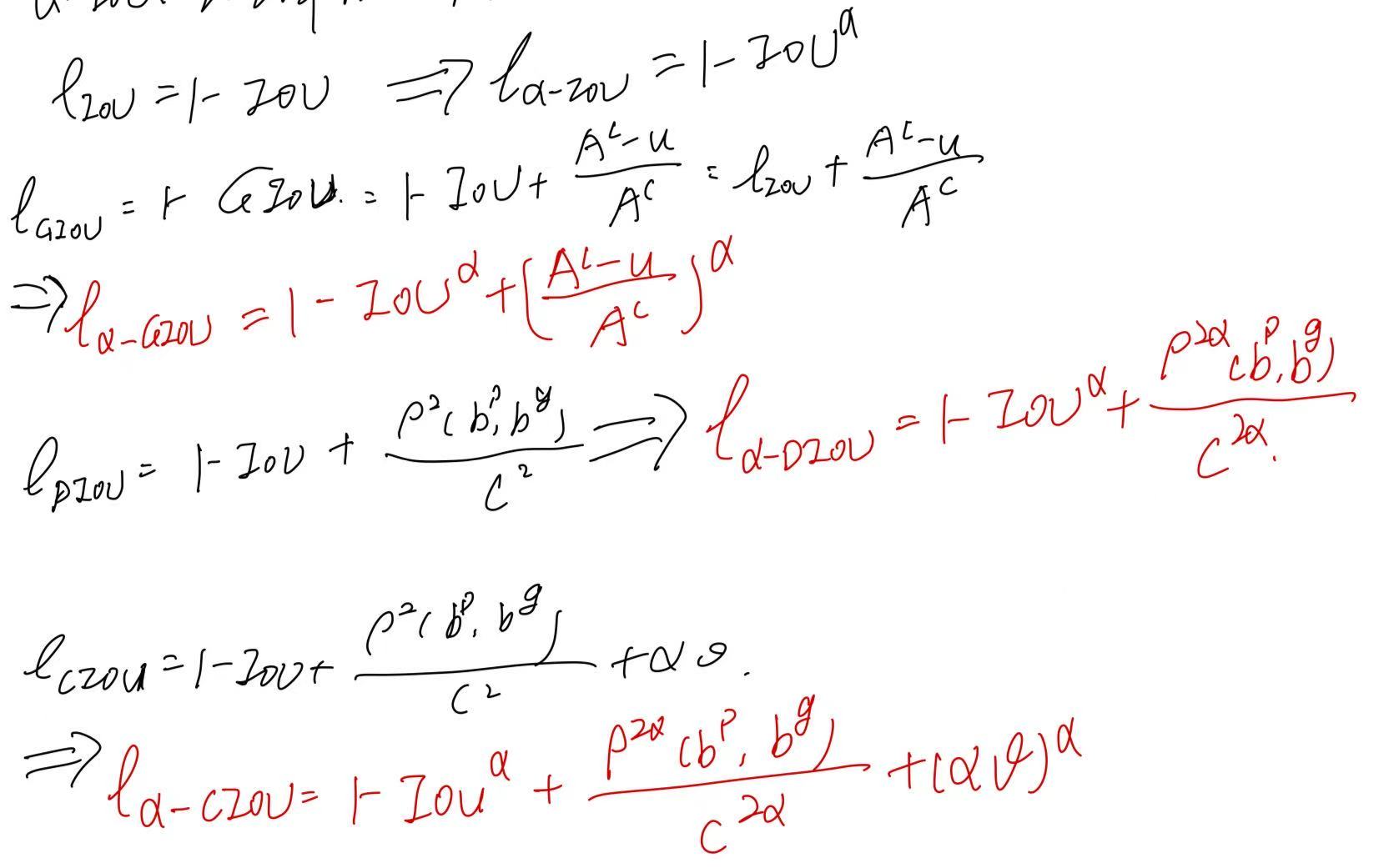
目标检测中的损失函数(二) | BIoU RIoU α-IoU
BIoU来自发表在2018年CVPR上的文章:《Improving Object Localization With Fitness NMS and Bounded IoU Loss》 论文针对现有目标检测方法只关注“足够好”的定位,而非“最优”的框,提出了一种考虑定位质量的NMS策略和BIoU loss。 这里不赘…...
 - 什么是MCP)
SpringAI系列 - MCP篇(一) - 什么是MCP
目录 一、引言二、MCP核心架构三、MCP传输层(stdio / sse)四、MCP能力协商机制(Capability Negotiation)五、MCP Client相关能力(Roots / Sampling)六、MCP Server相关能力(Prompts / Resources / Tools)一、引言 之前我们在接入大模型时,不同的大模型通常都有自己的…...

Linux 入门十一:Linux 网络编程
一、概述 1. 网络编程基础 网络编程是通过网络应用编程接口(API)编写程序,实现不同主机上进程间的信息交互。它解决的核心问题是:如何让不同主机上的程序进行通信。 2. 网络模型:从 OSI 到 TCP/IP OSI 七层模型&…...

沐渥氮气柜控制板温湿度氧含量氮气流量四显智控系统
氮气柜控制板通常用于实时监控和调节柜内环境参数,确保存储物品如电子元件、精密仪器、化学品等,处于低氧、干燥的稳定状态。以下是沐渥氮气柜控制板核心参数的详细介绍及控制逻辑: 一、控制板核心参数显示模块 1)温度显示&am…...

vue3 主题模式 结合 element-plus的主题
vue3 主题模式 结合 element-plus的主题 npm i element-plus --save-dev在 Vue 3 中,实现主题模式主要有以下几种方式 1.使用 CSS 变量(自定义属性) CSS 变量是一种在 CSS 中定义可重用值的方式。在主题模式中,可以将颜色、字体…...
)
Redis 有序集合(Sorted Set)
Redis 有序集合(Sorted Set) 以下从基础命令、内部编码和使用场景三个维度对 Redis 有序集合进行详细解析: 一、基础命令 命令时间复杂度命令含义zadd key score member [score member …] O ( k l o g ( n ) ) O(klog(n)) O(klog(n))&…...

[c语言日寄]免费文档生成器——Doxygen在c语言程序中的使用
【作者主页】siy2333 【专栏介绍】⌈c语言日寄⌋:这是一个专注于C语言刷题的专栏,精选题目,搭配详细题解、拓展算法。从基础语法到复杂算法,题目涉及的知识点全面覆盖,助力你系统提升。无论你是初学者,还是…...

QtCreator的设计器、预览功能能看到程序图标,编译运行后图标消失
重新更换虚拟机(Vmware Kylin),重新编译和配置了很多第三方库后,将代码跑到新的这个虚拟机环境中,但是出现程序图标不可见,占位也消失,后来继续检查ui文件,ui文件图标也异常&#x…...

QT文件和文件夹拷贝操作
1.拷贝文件夹 //(源文件目录路劲,目的文件目录,文件存在是否覆盖) bool copyDirectory(const QString& srcPath, const QString& dstPath, bool coverFileIfExist) { QDir srcDir(srcPath); QDir dstDir(dstPath); if (!dstDir.exi…...

面试常用基础算法
目录 快速排序归并排序堆排序 n n n皇后问题最大和子数组爬楼梯中心扩展法求最长回文子序列分割回文串动态规划求最长回文子序列最长回文子串单调栈双指针算法修改 分割回文串滑动窗口栈 快速排序 #include <iostream> #include <algorithm>using namespace std;…...
