从项目真实场景中理解二分算法的细节(附图解和模板)
遇到一个真实场景里使用二分算法的问题,本以为可以放心交给小师弟去做,结果出现了各种问题,在此梳理下二分算法的核心思想和使用细节。
文章目录
- 1.场景描述
- 2.场景分析
- 3.二分算法的精髓
- 总结
1.场景描述
系统A中所有业务日志保存在持久化的日志文件中,日志文件每4小时保存为一个文件,日志大小不一。有可能某个时段下完全无日志(如凌晨时段)。
现在发现,在过去的某次变更中,有一个业务问题当成通用异常处理掉了,异常中包含了一些业务参数,依据这些参数可以进行一个简单的校验 f f f,来校验是否出现了这个问题。
现在我们需要找出最早出现这个异常的时间点,进行后续的数据分析和策略制定。
2.场景分析
由于变更时间已久,排查历史变更及代码成本过高,最好的办法是读日志,确定具体的时间区间,从而做后续措施。
日志的时间区间跨度过大,粗略估计可能的时间区间为450天。一一读日志文件,可能最多需要2700次左右的IO,按最后的准确结果来看,从区间起点开始查找,也需要1400次左右的IO。
仔细分析,该时间区间,针对是否存在该问题的情况,可以变为一个 { 0 , 1 } \{0,1\} {0,1}的数组,而且本身是有序的,区间为 { 0 , 0 , 0 ⏟ n 个 0 . . . 1 , 1 , 1 , 1 ⏟ m 个 1 } \{\underbrace{0,0,0}_{n个0}...\underbrace{1,1,1,1}_{m个1}\} {n个0 0,0,0...m个1 1,1,1,1}。对这个区间进行二分的话,只需要 log 2 ( 2700 ) = 12 \log_{2}(2700)=12 log2(2700)=12次IO即可。
3.二分算法的精髓
二分理解起来简单,就是每次找另一半,能把复杂度降到log级别,但在实际运用过程中,经常会有类似数组下标越界、死循环、答案错误等问题,根本原因在于没有完全理解实际场景在二分搜索中的过程。
3.1 核心模板
二分算法的核心模板如下:
int l = [左边界], r = [右边界];
while([在区间内]) {int m = [取左右边界的中点];if([m是否符合要求]) {[移动左或右区间](相当于排除一半区间)} else {[移动左或右区间](相当于排除一半区间)}
}
return [结果];
接下来就是依据具体的问题将这个模板实例化,在实例化的过程中,就需要解决以下几个问题:
- 左右边界怎么取?
- 如何判断在区间内?
- 如何取中点?
- 如何移动区间?
- 如何取到想要的结果?
如果只是对二分有过简单的理解,那么抠这些细节将会非常的难受。接下来我们可以显看一个实际的例子,放慢二分的每一步,从中去发现细节之处。
3.2 二分过程图解
先上一个经典的解决这个问题的代码:(至于为什么这么写分析完过程再讲)
public static int binarySearchClosed(int[] arr) {int left = 0;int right = arr.length - 1;while (left <= right) {int mid = left + (right - left) / 2;if (check(arr, mid)) {right = mid - 1;} else {left = mid + 1;}}return left;}
为了简化过程,省去文件读取、文件指针移动的过程,只保留核心逻辑: a r r arr arr为 { 0 , 1 } \{0,1\} {0,1}数组且有序, a r r [ i ] = 1 arr[i]=1 arr[i]=1表示该天的日志出现了问题。我们的目标是找到最小的 i i i,使得 a r r [ i ] = 1 arr[i]=1 arr[i]=1。
我们以以下数组为例:

接下来模拟程序的执行流程:
1.初始时候, L = 0 , R = 8 L=0,R=8 L=0,R=8。

2.此时的 L L L和 R R R满足 L ≤ R L\leq R L≤R,计算 M = ( 0 + 8 ) / 2 = 4 M=(0+8)/2=4 M=(0+8)/2=4。

3.此时 c h e c k ( M ) = 0 check(M)=0 check(M)=0,说明区间 [ L , M ] [L,M] [L,M]可以直接排除,用红色标记,并更新 L = M + 1 = 5 L=M+1=5 L=M+1=5。

4.此时的 L L L和 R R R满足 L ≤ R L\leq R L≤R,计算 M = ( 5 + 8 ) / 2 = 6 M=(5+8)/2=6 M=(5+8)/2=6。

5.此时 c h e c k ( M ) = 1 check(M)=1 check(M)=1,说明区间 [ M , R ] [M,R] [M,R]都是符合条件的,用蓝色标记,但是我们需要找最小的符合条件的,所以需要在这个区间的左边去找,更新 R = M − 1 = 5 R=M-1=5 R=M−1=5。

6.此时的 L L L和 R R R满足 L ≤ R L\leq R L≤R,计算 M = ( 5 + 5 ) / 2 = 5 M=(5+5)/2=5 M=(5+5)/2=5。

7.此时 c h e c k ( M ) = 0 check(M)=0 check(M)=0,说明区间 [ L , M ] [L,M] [L,M]( [ 5 , 5 ] [5,5] [5,5])可以直接排除,用红色标记,所以更新 L = M + 1 = 6 L=M+1=6 L=M+1=6。

8.此时 L > R L>R L>R,不满足循环条件,退出循环,并返回 L L L。
通过上述的图解过程,我们可以得出以下细节:
- 初始选取的 L L L和 R R R是数组中的有效下标,也就是说能在二分的过程中取到的,相当于循环一直在闭区间 [ L , R ] [L,R] [L,R]中操作。
- 只要我们操作的区间不为空,就可以一直循环下去,区间不为空的条件就是 L ≤ R L\leq R L≤R。
- 每次判断 M M M是否符合条件后,我们都可以排除一半不符合条件的数。
- 循环结束时, L = R + 1 L=R+1 L=R+1, L L L指向第一个符合条件的数, R R R指向不符合条件的最后一个数。
从整个二分的过程来看,其实就是不断缩小操作区间的过程,当区间为空,原始的大区间已经分为了红蓝两部分,红色部分不符合条件,蓝色部分符合条件,而左指针指向蓝色区间的起点,右指针指向红色区间的终点。
基于此代码和思想,其实我们已经可以拓展出解决任何二分问题的思路了,只需要确定:
- 需要操作的二分区间边界为多少。
- 如何判断二分中点是否满足答案。
- 二分结束后我需要的是什么结果。
例如(基础数量关系):
1.在一个有序数组中(区间为整个数组),找大于等于x的最小下标。(check函数写成 a r r [ m ] > = t a r g e t arr[m]>=target arr[m]>=target)
2.在一个有序数组中,找大于x的最小下标。(check函数写成 a r r [ m ] > t a r g e t arr[m]>target arr[m]>target)
3.在一个有序数组中,找小于等于x的最大下标。(等价于【找大于x的最小下标】 - 1)
4.在一个有序数组中,找小于x的最大下标。(等价于【找大于等于x的最小下标】 - 1)
核心就是变动check函数以及循环结束后左右指针的指向。
3.3 各种区间写法
经常会看到有些会把初始条件写为: L = − 1 L=-1 L=−1或 R = N R=N R=N(数组长度),其实本质上是操作的区间不一样,不一样的初始区间,会导致循环条件、区间移动方法、最终结果有所不同,但核心思想都是一样的。
一般来说,二分的写法分为三种:闭区间、半闭半开区间、开区间。
当整个区间的分布为:前一段不满足条件,后一段满足条件,有以下的细节。
3.3.1 闭区间二分查找 [ l e f t , r i g h t ] [left, right] [left,right]
- 搜索范围始终保持在闭区间 [ l e f t , r i g h t ] [left, right] [left,right] 内
- 循环条件为 l e f t < = r i g h t left <= right left<=right
- 当 c h e c k ( a r r [ m i d ] ) = = t r u e check(arr[mid])==true check(arr[mid])==true 时,搜索区间变为 [ l e f t , m i d − 1 ] [left, mid-1] [left,mid−1]
- 当 c h e c k ( a r r [ m i d ] ) = = f a l s e check(arr[mid])==false check(arr[mid])==false时,搜索区间变为 [ m i d + 1 , r i g h t ] [mid+1, right] [mid+1,right]
- 循环退出时: l e f t > r i g h t left > right left>right
- l e f t left left 指向第一个符合要求的位置
- r i g h t right right 指向最后一个不符合要求的位置
3.3.2 半闭半开区间二分查找 [ l e f t , r i g h t ) [left, right) [left,right)
- 搜索范围为 [ l e f t , r i g h t ) [left, right) [left,right),包含 l e f t left left但不包含 r i g h t right right
- 循环条件为 l e f t < r i g h t left < right left<right
- 当 c h e c k ( a r r [ m i d ] ) = = t r u e check(arr[mid])==true check(arr[mid])==true 时,搜索区间变为 [ l e f t , m i d ) [left, mid) [left,mid)
- 当 c h e c k ( a r r [ m i d ] ) = = f a l s e check(arr[mid])==false check(arr[mid])==false 时,搜索区间变为 [ m i d + 1 , r i g h t ) [mid+1, right) [mid+1,right)
- 循环退出时: l e f t = = r i g h t left == right left==right
- l e f t / r i g h t left/right left/right 都指向第一个符合要求的位置
- 如果数组中没有符合要求的位置,则 l e f t / r i g h t left/right left/right 等于 a r r . l e n g t h arr.length arr.length
3.3.3 开区间二分查找 ( l e f t , r i g h t ) (left, right) (left,right)
- 搜索范围为 ( l e f t , r i g h t ) (left, right) (left,right),不包含 l e f t left left和 r i g h t right right
- 初始化时 l e f t = − 1 left = -1 left=−1, r i g h t = a r r . l e n g t h right = arr.length right=arr.length
- 循环条件为 l e f t + 1 < r i g h t left + 1 < right left+1<right
- 当 c h e c k ( a r r [ m i d ] ) = = t r u e check(arr[mid])==true check(arr[mid])==true 时,搜索区间变为 ( l e f t , m i d ) (left, mid) (left,mid)
- 当 c h e c k ( a r r [ m i d ] ) = = f a l s e check(arr[mid])==false check(arr[mid])==false时,搜索区间变为 ( m i d , r i g h t ) (mid, right) (mid,right)
- 循环退出时: r i g h t = l e f t + 1 right = left + 1 right=left+1
- r i g h t right right 指向第一个符合要求的位置
- l e f t left left 指向最后一个不符合要求的位置
总结
二分算法是一种巧妙的思想,在面对一些逻辑上有序的问题时,可以迅速的排除掉一半的区间,从而能在log级别的时间内找出需要的答案。落实到代码上时,会有各种细节问题,但只要理解到二分的核心思想,将其视为一个不断缩小区间的过程,很快就能找到自己实现二分问题的节奏。希望本文的出发点能对你有所帮助。
ATFWUS 2025-04-22
相关文章:

从项目真实场景中理解二分算法的细节(附图解和模板)
遇到一个真实场景里使用二分算法的问题,本以为可以放心交给小师弟去做,结果出现了各种问题,在此梳理下二分算法的核心思想和使用细节。 文章目录 1.场景描述2.场景分析3.二分算法的精髓3.1 核心模板3.2 二分过程图解3.3 各种区间写法3.3.1 闭…...

金融图QCPFinancial
QCPFinancial 是 QCustomPlot 中用于绘制金融图表(如蜡烛图/K线图)的核心类。以下是其关键特性的详细说明: 一、主要属性 属性类型说明dataQSharedPointer<QCPFinancialDataContainer>存储金融数据的数据容器chartStyleQCPFinancial:…...

Jetson Orin NX 16G 配置GO1强化学习运行环境
这一次收到了Jrtson Orin NX, 可以进行部署了。上一次在nano上的失败经验 Jetson nano配置Docker和torch运行环境_jetson docker-CSDN博客 本次的目的是配置cuda-torch-python38环境离机运行策略。 Jetson Orin NX SUPER 1. 烧录镜像 参考链接在ubuntu系统中安装sdk manag…...

文档管理 Document Management
以下是关于项目管理中 文档管理 的深度解析,结合高项(如软考高级信息系统项目管理师)教材内容,系统阐述文档管理的理论框架、核心流程及实战应用: 一、文档管理的基本概念 1. 定义 文档管理是对项目全生命周期中产生的各类文档进行规范化管理的过程,包括创建、存储、版…...

【Pandas】pandas DataFrame truediv
Pandas2.2 DataFrame Binary operator functions 方法描述DataFrame.add(other)用于执行 DataFrame 与另一个对象(如 DataFrame、Series 或标量)的逐元素加法操作DataFrame.add(other[, axis, level, fill_value])用于执行 DataFrame 与另一个对象&…...

Linux 内核中 cgroup 子系统 cpuset 是什么?
cpuset 是 Linux 内核中 cgroup(控制组) 的一个子系统,用于将一组进程(或任务)绑定到特定的 CPU 核心和 内存节点(NUMA 节点)上运行。它通过限制进程的 CPU 和内存资源的使用范围,优…...

Windows 同步-互锁变量访问
互锁变量访问 应用程序必须同步对多个线程共享的变量的访问。 应用程序还必须确保对这些变量的作以原子方式执行(完全或根本不执行)。 对正确对齐的 32 位变量的简单读取和写入是原子作。 换句话说,你最终不会只更新变量的一部分;所有位都以…...

深度学习3.5 图像分类数据集
%matplotlib inline import torch import torchvision from torch.utils import data from torchvision import transforms from d2l import torch as d2l代码执行流程图 #mermaid-svg-WWhBmQvijswiICpI {font-family:"trebuchet ms",verdana,arial,sans-serif;font-…...

js原型链prototype解释
function Person(){} var personnew Person() console.log(啊啊,Person instanceof Function);//true console.log(,Person.__proto__Function.prototype);//true console.log(,Person.prototype.__proto__ Object.prototype);//true console.log(,Function.prototype.__prot…...

从M个元素中查找最小的N个元素时,使用大顶堆的效率比使用小顶堆更高,为什么?
我们有一个长度为 M 的数组,现在我们想从中找出 最小的 N 个元素。例如: int a[10] {12, 3, 5, 7, 19, 0, 8, 2, 4, 10};从中找出 最小的 4 个元素。 正确方法:使用大小为 N 的「大顶堆」 原因分析: 我们想保留最小的 4 个元素…...

【知识】性能优化和内存优化的主要方向
转载请注明出处:小锋学长生活大爆炸[xfxuezhagn.cn] 如果本文帮助到了你,欢迎[点赞、收藏、关注]哦~ 前言 现在有很多论文,乍一看很高级,实际上一搜全是现有技术的堆砌,但是这种裁缝式的论文依然能发表在很好的会议和期…...

VS Code + GitHub:高效开发工作流指南
目录 一、安装 & 基本配置 1.下载 VS Code 2.安装推荐插件(打开侧边栏 Extensions) 3.设置中文界面(可选) 二、使用 VS Code 操作 Git/GitHub 1.基本 Git 操作(不输命令行!) 2.连接 GitHub(第一次使用) 三、克隆远程仓库到 VS Code 方法一(推荐): 方…...

软件测试之接口测试常见面试
一、什么是(软件)接口测试? 接口测试:是测试系统组件间接口的一种测试方法 接口测试的重点:检查数据的交换,数据传递的正确性,以及接口间的逻辑依赖关系 接口测试的意义:在较早期开展,在软件开发的同时…...

发送百度地图的定位
在vuephp写的聊天软件项目中,增加一个发送百度地图的定位功能 在 Vue PHP 的聊天软件中增加发送百度地图定位功能,需要从前端定位获取、地图API集成、后端存储到消息展示全流程实现。以下是详细步骤: 一、前端实现(Vue/Uni-app…...
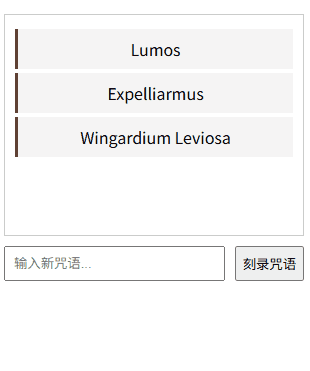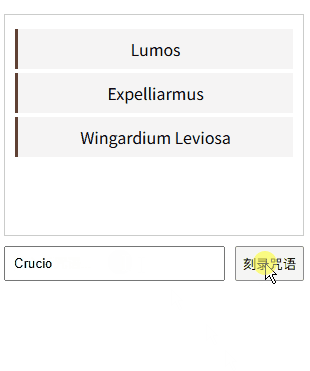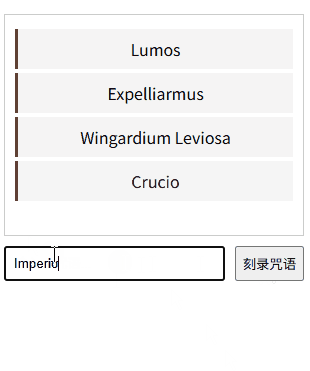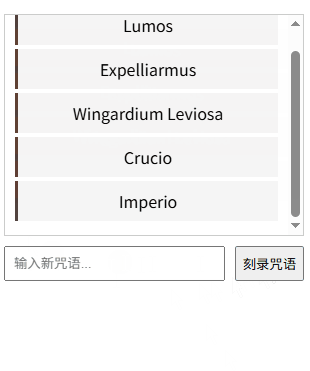
11、Refs:直接操控元素——React 19 DOM操作秘籍
一、元素操控的魔法本质 "Refs是巫师与麻瓜世界的连接通道,让开发者能像操控魔杖般精准控制DOM元素!"魔杖工坊的奥利凡德先生轻抚着魔杖,React/Vue的refs能量在杖尖跃动。 ——以神秘事务司的量子纠缠理论为基,揭示DOM…...

uniapp-商城-33-shop 布局搜索页面以及u-search
shop页面上有一个搜索,可以进行商品搜索,这里我们先做一个页面布局,后面再来进行数据i联动。 1、shop页面的搜索 2、搜索的页面代码 <navigator class"searchView" url"/pagesub/pageshop/search/search"> …...

npm的基本使用安装所有包,安装删除指定版本的包,配置命名别名
npm的基本使用安装所有包,安装删除指定版本的包,配置命名别名 安装所有依赖指定版本安装/删除包给 npm 脚本配置“命令别名(自定义命令)” ✅ 一、安装所有包(恢复依赖) 如果项目中已经存在 package.json…...

【dataframe显示不全问题】打开一个行列超多的excel转成df之后行列显示不全
出现问题如下图: 解决方案~ display.width解决列显示不全 pd.set_option(display.max_columns,1000) pd.set_option(display.width, 1000) pd.set_option(display.max_colwidth,1000) pd.set_option(display.max_rows,1000)...

Windows下Golang与Nuxt项目宝塔部署指南
在Windows下将Golang后端和Nuxt前端项目打包,并使用宝塔面板部署的步骤如下 一、Golang后端打包 交叉编译为Linux可执行文件 在Windows PowerShell中执行: powershell复制下载 $env:GOOS "linux" $env:GOARCH "amd64" go build…...

真实趋势策略思路
该交易策略通过一系列技术指标的计算与逻辑判断,旨在捕捉市场趋势的反转与延续点,以实现盈利。其主要交易逻辑思路可以概括如下: 1. 趋势与动量分析 策略首先利用动量函数计算收盘价的短期(3周期)变化,通过…...

江奇霖惊喜亮相泡泡岛音乐节,新歌首唱+合作舞台燃动现场
2025年4月20日,江奇霖受邀参加2025泡泡岛音乐与艺术节东南站。现场献唱三首歌曲,超5万名观众现场一同感受音乐的魅力。 在泡泡岛SPECIAL SET特别企划舞台中,江奇霖带来新歌的首唱,温暖的旋律如低语倾诉,观众们也纷纷喊…...

【HarmonyOS】ArKUI框架
目录 概述 声明式开发范式 基于ArKUI的项目 • 1.创建资源文件 • 2.引用资源 • 3.引用系统资源: • 系统资源有哪些 • 4. 在配置和资源中引用资源 声明式语法 UI描述规范 UI组件概述 组件化 组件渲染控制语法 修改…...

使用 Nacos 的注意事项与最佳实践
📹 背景 Nacos 凭借其强大💪的服务发现、配置管理和服务管理能力,成为构建分布式系统的得力助手。然而,要充分发挥 Nacos 的优势,实现系统的高性能、高可用,掌握其使用过程中的注意事项和最佳实践至关…...

Megatron - LM 重要文件解析 - /tools/preprocess_data.py
preprocess_data.py 的主要功能。这是 Megatron-LM 的数据预处理脚本,主要用于将原始文本数据转换为模型训练所需的格式。 核心功能: 1. 数据预处理流程: 输入:原始文本文件(JSON格式) 处理:…...

计算机网络八股——HTTP协议与HTTPS协议
目录 HTTP1.1简述与特性 1. 报文清晰易读 2. 灵活和易于扩展 3. ⽆状态 Cookie和Session 4. 明⽂传输、不安全 HTTP协议发展过程 HTTP/1.1的不足 HTTP/2.0 HTTP/3.0 HTTPS协议 HTTP协议和HTTPS协议的区别 HTTPS中的加密方式 HTTPS中建立连接的方式 前言ÿ…...

Unitest和pytest使用方法
unittest 是 Python 自带的单元测试框架,用于编写和运行可重复的测试用例。它的核心思想是通过断言(assertions)验证代码的行为是否符合预期。以下是 unittest 的基本使用方法: 1. 基本结构 1.1 创建测试类 继承 unittest.TestC…...

常用python爬虫框架介绍
文章目录 前言1. Scrapy2. BeautifulSoup 与 Requests 组合3. Selenium4. PySpider 前言 Python 有许多优秀的爬虫框架,每个框架都有其独特的特点和适用场景。以下为你详细介绍几个常用的 Python 爬虫框架: Python 3.13.2 安装教程(附安装包…...
2.3 预训练自己的模型)
AI大模型:(二)2.3 预训练自己的模型
目录 1.预训练原理 2.预训练范式 1.未标注数据 2.标注数据 3.有正确答案、也有错误答案 3.手撕transform模型 3.1.transform模型代码 3.2.训练数据集 3.3.预训练 3.4.推理 4.如何选择模型 5.如何确定模型需要哪种训练 大模型预训练(Large-scale Pre-training…...

webpack基础使用了解(入口、出口、插件、加载器、优化、别名、打包模式、环境变量、代码分割等)
目录 1、webpack简介2、简单示例3、入口(entry)和输出(output)4、自动生成html文件5、打包css代码6、优化(单独提取css代码)7、优化(压缩过程)8、打包less代码9、打包图片10、搭建开发环境(webpack-dev-server…...
:时钟树综合——让芯片的「心跳」同步到每个角落)
数字后端设计 (四):时钟树综合——让芯片的「心跳」同步到每个角落
—— 试想全城的人要在同一秒按下开关——如果有的表快、有的表慢,结果会乱套!时钟树综合就是给芯片内部装一套精准的“广播对时系统”,让所有电路踩着同一个节拍工作。 1. 为什么时钟如此重要? 芯片的「心跳」:时钟信…...
