专题讨论2:树与查找

在讨论前先回顾一下定义:
BST树的定义
二叉搜索树是一种特殊的二叉树,对于树中的任意一个节点:
若它存在左子树,那么左子树中所有节点的值都小于该节点的值。
若它存在右子树,那么右子树中所有节点的值都大于该节点的值。
它的左、右子树也分别是二叉搜索树。
总结就是:左<根<右
特性
有序性:二叉搜索树对节点值的大小关系有严格规定,这使得它天然具备了一定的有序性。
例如,对二叉搜索树进行中序遍历,会得到一个升序排列的节点值序列。
查找高效性:基于其节点值的大小关系特性,在二叉搜索树中查找一个节点时,平均情况下时间复杂度为,其中 n 是树中节点的数量。这是因为每次比较都能排除大约一半的搜索空间,类似于二分查找。
那既然回顾好了相关概念我们就可以进入正题了。如何用代码实现BST树上的查找、添加与删除呢?
基本思路
查找:从根节点开始,将目标值与当前节点值比较。若相等则找到;若目标值小于当前节点值,就到左子树继续查找;若大于,则到右子树查找。
添加(插入):同样从根节点开始比较,若目标值小于当前节点值且当前节点左子树为空,就在此处插入;若左子树不为空,就继续在左子树重复该过程。若目标值大于当前节点值,操作类似,只是在右子树进行。
删除:删除节点情况相对复杂。若删除的是叶子节点,直接删除即可;若节点只有一个子树,用子树替代该节点;若节点有两个子树,通常找到其右子树中的最小节点(或左子树中的最大节点)来替代它,然后再删除该替代节点 。
自然语言描述
1、二叉搜索树的节点结构:
定义一个 TreeNode 结构体来表示二叉搜索树的节点。每个节点包含三个成员:
val:存储节点的值。
left:指向该节点左子节点的指针,初始化为 nullptr。
right:指向该节点右子节点的指针,初始化为 nullptr。
构造函数 TreeNode(int x):用于方便地创建节点并初始化其值,同时将左右子节点指针初始化为 nullptr。
2、查找节点函数 search
1)首先判断根节点 root 是否为空,或者根节点的值是否等于要查找的值 val ,如果满足条件则直接返回当前根节点(如果为空表示没找到,如果值相等表示找到了)。
2)根节点不为空且值不等于 val 的话,就比较 val 和根节点的值 root->val :
- 若 val 小于 root->val ,则递归地在根节点的左子树中查找,即 return search(root->left, val) 。
- 若 val 大于 root->val ,则递归地在根节点的右子树中查找,即 return search(root->right, val) 。
3、插入节点函数 insert
1)首先判断根节点 root 是否为空,如果为空,就创建一个新节点并返回,新节点的值为 val。
2)根节点不为空的话,就比较 val 和根节点的值 root->val:
- 若 val 小于 root->val ,则递归地在根节点的左子树中插入新节点,即 root->left = insert(root->left, val) 。
- 若 val 大于等于 root->val ,则递归地在根节点的右子树中插入新节点,即 root->right = insert(root->right, val) 。
3)返回插入节点后的根节点。
4、查找最小节点函数 findMin(为删除函数做准备)
函数 findMin 用于在给定的子树中找到值最小的节点。因为在二叉搜索树中,最左下方的节点值最小,所以通过一个循环不断向左子节点移动,直到左子节点为空,此时当前节点就是该子树中值最小的节点,然后返回该节点。
5、删除节点函数 deleteNode
1)首先判断根节点 root 是否为空,如果为空,直接返回 root 。
2)根节点不为空的话,就比较 val 和根节点 root->val :
- 若 val 小于 root->val ,则递归地在根节点的左子树中删除值为 val 的节点,即 root->left = deleteNode(root->left, val) 。
- 若 val 大于 root->val ,则递归地在根节点的右子树中删除值为 val 的节点,即 root->right = deleteNode(root->right, val) 。
- 若 val 等于 root->val ,说明找到了要删除的节点,此时应分情况处理:
- 如果当前节点的左子树为空,那就直接用右子节点替换当前节点。(将右子节点的指针保存到临时变量 temp 中,然后释放当前节点的内存,最后返回 temp)
- 如果当前节点的右子树为空,那么用左子节点替换当前节点。(先将左子节点的指针保存到 temp 中,释放当前节点的内存,最后返回 temp)
- 当左右子树都不为空时,找到右子树中的最小节点(该节点的值小于右子树所有节点的值且大于左子树中所有节点的值),用该最小节点的值替换当前节点的值,然后递归地在右子树中删除这个最小节点。
伪代码
// 定义二叉搜索树的节点结构
结构体 TreeNode:整数 val指针 left 指向 TreeNode指针 right 指向 TreeNode构造函数 TreeNode(整数 x):val = xleft = 空指针right = 空指针// 查找操作
函数 search(指针 root 指向 TreeNode, 整数 val):如果 root 为空指针 或者 root->val 等于 val:返回 root如果 val < root->val:返回 search(root->left, val)否则:返回 search(root->right, val)// 插入操作
函数 insert(指针 root 指向 TreeNode, 整数 val):如果 root 为空指针:返回 新创建的 TreeNode(val)如果 val < root->val:root->left = insert(root->left, val)否则:root->right = insert(root->right, val)返回 root// 查找最小节点
函数 findMin(指针 node 指向 TreeNode):当 node->left 不为空指针 时:node = node->left返回 node// 删除操作
函数 deleteNode(指针 root 指向 TreeNode, 整数 val):如果 root 为空指针:返回 root如果 val < root->val:root->left = deleteNode(root->left, val)否则 如果 val > root->val:root->right = deleteNode(root->right, val)否则:如果 root->left 为空指针:临时指针 temp 指向 root->right删除 root返回 temp否则 如果 root->right 为空指针:临时指针 temp 指向 root->left删除 root返回 temp临时指针 temp 指向 findMin(root->right)root->val = temp->valroot->right = deleteNode(root->right, temp->val)返回 root代码实现
#include <iostream>
using namespace std;// 定义二叉搜索树的节点结构
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};// 查找
TreeNode* search(TreeNode* root, int val) {if (root == nullptr || root->val == val) {return root;}if (val < root->val) {return search(root->left, val);}else {return search(root->right, val);}
}// 插入
TreeNode* insert(TreeNode* root, int val) {if (root == nullptr) {return new TreeNode(val);}if (val < root->val) {root->left = insert(root->left, val);}else {root->right = insert(root->right, val);}return root;
}
// 找到最小值
TreeNode* findMin(TreeNode* node) {while (node->left != nullptr) {node = node->left;}return node;
}
// 删除
TreeNode* deleteNode(TreeNode* root, int val) {if (root == nullptr) {return root;}if (val < root->val) {root->left = deleteNode(root->left, val);}else if (val > root->val) {root->right = deleteNode(root->right, val);}else {if (root->left == nullptr) {TreeNode* temp = root->right;delete root;return temp;}else if (root->right == nullptr) {TreeNode* temp = root->left;delete root;return temp;}TreeNode* temp = findMin(root->right);root->val = temp->val;root->right = deleteNode(root->right, temp->val);}return root;
}// 中序遍历打印树
void inorder(TreeNode* root) {if (root != nullptr) {inorder(root->left);cout << root->val << " ";inorder(root->right);}
}int main() {TreeNode* root = nullptr;int num;cout << "输入一系列整数来构建二叉搜索树,输入 -1 结束输入:" << endl;while (true) {cin >> num;if (num == -1) break;root = insert(root, num);}cout << "中序遍历构建的二叉搜索树:";inorder(root);cout << endl;while (true) {cout << "请选择操作:" << endl;cout << "1. 查找节点" << endl;cout << "2. 插入节点" << endl;cout << "3. 删除节点" << endl;cout << "4. 退出程序" << endl;int choice;cin >> choice;if (choice == 1) {cout << "请输入要查找的节点值:";cin >> num;TreeNode* found = search(root, num);if (found != nullptr) {cout << "找到节点:" << found->val << endl;}else {cout << "未找到节点。" << endl;}}else if (choice == 2) {cout << "请输入要插入的节点值:";cin >> num;root = insert(root, num);cout << "插入成功,插入后的中序遍历结果:";inorder(root);cout << endl;}else if (choice == 3) {cout << "请输入要删除的节点值:";cin >> num;root = deleteNode(root, num);cout << "删除操作完成,删除后的中序遍历结果:";inorder(root);cout << endl;}else if (choice == 4) {break;}else {cout << "无效的选择,请重新输入。" << endl;}}return 0;
}因为要实现大数据插入并可视化展现,不知道为啥我这里安装不了那个应用,于是乎我让 AI 帮我修改了一下我的代码:
修改后的代码如下
#include <iostream>
#include <cstdlib>
#include <ctime>
using namespace std;// 定义二叉搜索树的节点结构
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};// 查找,同时统计比较次数
int search(TreeNode* root, int val, int& comparisons) {comparisons++;if (root == nullptr || root->val == val) {return comparisons;}if (val < root->val) {return search(root->left, val, comparisons);}else {return search(root->right, val, comparisons);}
}// 插入
TreeNode* insert(TreeNode* root, int val) {if (root == nullptr) {return new TreeNode(val);}if (val < root->val) {root->left = insert(root->left, val);}else {root->right = insert(root->right, val);}return root;
}// 找到最小值
TreeNode* findMin(TreeNode* node) {while (node->left != nullptr) {node = node->left;}return node;
}// 删除
TreeNode* deleteNode(TreeNode* root, int val) {if (root == nullptr) {return root;}if (val < root->val) {root->left = deleteNode(root->left, val);}else if (val > root->val) {root->right = deleteNode(root->right, val);}else {if (root->left == nullptr) {TreeNode* temp = root->right;delete root;return temp;}else if (root->right == nullptr) {TreeNode* temp = root->left;delete root;return temp;}TreeNode* temp = findMin(root->right);root->val = temp->val;root->right = deleteNode(root->right, temp->val);}return root;
}// 计算树的高度
int treeHeight(TreeNode* root) {if (root == nullptr) {return 0;}int leftHeight = treeHeight(root->left);int rightHeight = treeHeight(root->right);return max(leftHeight, rightHeight) + 1;
}// 中序遍历打印树
void inorder(TreeNode* root) {if (root != nullptr) {inorder(root->left);cout << root->val << " ";inorder(root->right);}
}int main() {srand(static_cast<unsigned int>(time(nullptr)));TreeNode* root = nullptr;const int numToGenerate = 100000;const int rangeMin = 1;const int rangeMax = 1000000;// 生成并插入随机数构建BSTfor (int i = 0; i < numToGenerate; ++i) {int randomNum = rangeMin + rand() % (rangeMax - rangeMin + 1);root = insert(root, randomNum);}cout << "二叉搜索树构建完成,树的高度为:" << treeHeight(root) << endl;const int numToSearch = 10000;int totalComparisons = 0;for (int i = 0; i < numToSearch; ++i) {int randomSearchNum = rangeMin + rand() % (rangeMax - rangeMin + 1);int comparisons = 0;search(root, randomSearchNum, comparisons);totalComparisons += comparisons;}double averageComparisons = static_cast<double>(totalComparisons) / numToSearch;cout << "随机查找的平均比较次数为:" << averageComparisons << endl;// 计算ASL(这里简单遍历所有节点,实际可根据具体需求优化)int aslTotalComparisons = 0;int nodeCount = 0;// 辅助函数进行遍历计算,这里省略具体实现// 假设已有函数countASL遍历树计算总比较次数和节点数// countASL(root, aslTotalComparisons, nodeCount);double asl = static_cast<double>(aslTotalComparisons) / nodeCount;cout << "该树的ASL为:" << asl << endl;return 0;
}修改的地方分别是:
1)生成随机数并构建 BST:使用<cstdlib>和<ctime>库,利用rand()函数在指定范围内生成 10 万个随机数,调用insert函数构建二叉搜索树。
2)输出树的高度:编写计算二叉搜索树高度的函数,通过递归计算左右子树高度并取较大值加 1(根节点自身占一层),在构建树后调用该函数输出高度。
3)随机查找并统计平均比较次数:生成 1 万个随机数,对每个随机数调用search函数查找,在search函数中添加计数变量统计比较次数,最后求平均比较次数。
4)计算 ASL(平均查找长度):可以遍历所有节点,计算每个节点查找时的比较次数,再求平均值得到 ASL 。
各函数的时间复杂度和空间复杂度:
1、insert 函数
时间复杂度:
空间复杂度:
2、search 函数
时间复杂度:
空间复杂度:
3、findMin 函数
时间复杂度:
空间复杂度:
4、deleteNode 函数
时间复杂度:
空间复杂度:
5、 inorder 函数
时间复杂度:
空间复杂度:
运行结果

相关文章:

专题讨论2:树与查找
在讨论前先回顾一下定义: BST树的定义 二叉搜索树是一种特殊的二叉树,对于树中的任意一个节点: 若它存在左子树,那么左子树中所有节点的值都小于该节点的值。 若它存在右子树,那么右子树中所有节点的值都大于该节点…...

django之数据的翻页和搜索功能
数据的翻页和搜素功能 目录 1.实现搜素功能 2.实现翻页功能 一、实现搜素功能 我们到bootstrap官网, 点击组件, 然后找到输入框组, 并点击作为额外元素的按钮。 我们需要使用上面红色框里面的组件, 就是搜素组件, 代码部分就是下面红色框框出来的部分。 把这里的代码复制…...

盈达科技GEO供应商:用AICC智能认知攻防系统重构AI时代的“内容主权”
《盈达科技GEO供应商:用AICC智能认知攻防系统重构AI时代的“内容主权”》 ——从全网认知统一到多模态智能投喂,破解生成式AI的内容暗战 前言 当用户向ChatGPT提问“XX品牌空调质量如何”时,AI的回答可能直接决定企业30%的潜在客户流向。 生…...

unity脚本-FBX自动化模型面数校验
根据目前模型资源平均面数预算进行脚本制作,自动化校验模型面数是否符合规范。 *注:文件格式为.cs。需要放置在unity资源文件夹Assets>Editor下。 测试效果(拖一个fbx文件进unity时自动检测): 以下为完整代码 us…...

C++用于保留浮点数的两位小数,使用宏定义方法(可兼容低版本Visual Studio)
文章目录 一、 描述二、 样例二、 结果输出 一、 描述 这个宏定义(可放入.h头文件里)使用基本的数学运算,几乎兼容所有版本的VS,以下可对正数做四舍五入: #define ROUND_TO_TWO(x) ( (floor((x) * 100 0.5) / 100) …...

day30 学习笔记
文章目录 前言一、凸包特征检测1.穷举法2.QuickHull法 二、图像轮廓特征查找1.外接矩形2.最小外接矩形3.最小外接圆 前言 通过今天的学习,我掌握了OpenCV中有关凸包特征检测,图像轮廓特征查找的相关原理和操作 一、凸包特征检测 通俗的讲,凸…...

[密码学基础]密码学发展简史:从古典艺术到量子安全的演进
密码学发展简史:从古典艺术到量子安全的演进 密码学作为信息安全的基石,其发展贯穿人类文明史,从最初的文字游戏到量子时代的数学博弈,每一次变革都深刻影响着政治、军事、科技乃至日常生活。本文将以技术演进为主线,…...

(51单片机)LCD显示温度(DS18B20教程)(LCD1602教程)(延时函数教程)(单总线教程)
演示视频: LCD显示温度 源代码 如上图将9个文放在Keli5 中即可,然后烧录在单片机中就行了 烧录软件用的是STC-ISP,不知道怎么安装的可以去看江科大的视频: 【51单片机入门教程-2020版 程序全程纯手打 从零开始入门】https://www.…...

服务器运维:服务器流量的二八法则是什么意思?
文章目录 用户行为角度时间分布角度应用场景角度 服务器流量的二八法则,又称 80/20 法则,源自意大利经济学家帕累托提出的帕累托法则,该法则指出在很多情况下,80% 的结果是由 20% 的因素所决定的。在服务器流量领域,二…...

高并发秒杀使用RabbitMQ的优化思路
高并发秒杀使用RabbitMQ的优化思路 一、判断是否重复抢购(防止一人多次秒杀)的逻辑1. 整体逻辑代码2. 原始判断重复抢购的方式:3. 后来优化为什么用 Redis 判断? 二、高并发下优化过的秒杀逻辑1.秒杀核心逻辑(请求入口)…...

B + 树与 B 树的深度剖析
在数据库领域,B 树和 B 树是两种极为关键的数据结构,它们对于数据的存储、查询以及索引的构建等方面都有着深远的影响。深刻理解这两种树的原理、特性以及它们之间的差异,对于数据库的性能优化、数据组织和管理等工作具有不可替代的重要作用…...

【LeetCode】嚼烂热题100【持续更新】
2、字母异位词分组 方法一:排序哈希表 思路:对每个字符串排序,排序后的字符串作为键插入到哈希表中,值为List<String>形式存储单词原型,键为排序后的字符串。 Map<String, List<String>> m new Ha…...

赛灵思 XC7K325T-2FFG900I FPGA Xilinx Kintex‑7
XC7K325T-2FFG900I 是 Xilinx Kintex‑7 系列中一款工业级 (I) 高性能 FPGA,基于 28 nm HKMG HPL 工艺制程,核心电压标称 1.0 V,I/O 电压可在 0.97 V–1.03 V 之间灵活配置,并可在 –40 C 至 100 C 温度范围内稳定运行。该器件提供…...

【速写】多LoRA并行衍生的一些思考
迁移学习上的一个老问题,怎么做多领域的迁移?以前的逻辑认为领域迁移属于是对参数做方向性的调整,如果两个领域方向相左,实际上不管怎么加权相加都是不合理的。 目前一些做法想着去观察LoRA权重矩阵中的稠密块与稀疏块࿰…...

探索智能仓颉!Cangjie Magic:码字之间,意境自生
仓颉输入法,对于许多老牌中文使用者来说,不仅仅是一种输入工具,更是一种情怀,一种文化符号。它以拆字为核心,将汉字结构还原成最原始的构件,再通过特定的编码规则进行输入。然而,随着拼音输入法…...

py默认框架和代码
py默认框架 平常工作日常需要频繁写python脚本,留下一个常用的模板 # template.py import logging import json import time import functools import os from typing import Any, Dict, Optional, Union from pathlib import Path from logging.handlers import …...

通过 Samba 服务实现 Ubuntu 和 Windows 之间互传文件
在 Ubuntu 上进行配置 1. 安装 Samba 服务 打开终端,输入以下命令来安装 Samba: sudo apt update sudo apt install samba2. 创建共享目录 可以使用以下命令创建一个新的共享目录,例如创建名为 shared_folder 的目录: sudo m…...

k8s-1.28.10 安装metrics-server
1.简介 Metrics Server是一个集群范围的资源使用情况的数据聚合器。作为一个应用部署在集群中。Metric server从每个节点上KubeletAPI收集指标,通过Kubernetes聚合器注册在Master APIServer中。为集群提供Node、Pods资源利用率指标。 2.下载yaml文件 wget https:/…...

基于外部中中断机制,实现以下功能: 1.按键1,按下和释放后,点亮LED 2.按键2,按下和释放后,熄灭LED 3.按键3,按下和释放后,使得LED闪烁
题目: 参照外部中断的原理和代码示例,再结合之前已经实现的按键切换LED状态的实验,用外部中断改进其实现。 请自行参考文档《中断》当中,有关按键切换LED状态的内容, 自行连接电路图,基于外部中断机制,实现以下功能&am…...

【我的创作纪念日】 --- 与CSDN走过的第365天
个人主页:夜晚中的人海 不积跬步,无以至千里;不积小流,无以成江海。-《荀子》 文章目录 🎉一、机缘🚀二、收获🎡三、 日常⭐四、成就🏠五、憧憬 🎉一、机缘 光阴似箭&am…...

学习笔记——《Java面向对象程序设计》-继承
参考教材: Java面向对象程序设计(第3版)微课视频版 清华大学出版社 1、定义子类 class 子类名 extends 父类名{...... }如: class Student extends People{...... } (1)如果一个类的声明中没有extends关…...

鸿蒙生态新利器:华为ArkUI-X混合开发框架深度解析
鸿蒙生态新利器:华为ArkUI-X混合开发框架深度解析 作者:王老汉 | 鸿蒙生态开发者 | 2025年4月 📢 前言:开发者们的新机遇 各位鸿蒙开发者朋友们,是否还在为多平台开发重复造轮子而苦恼?今天给大家介绍一位…...

如何收集用户白屏/长时间无响应/接口超时问题
想象一下这样的场景:一位用户在午休时间打开某电商应用,准备购买一件心仪已久的商品。然而,页面加载了数秒后依然是一片空白,或者点击“加入购物车”按钮后没有任何反馈,甚至在结算时接口超时导致订单失败。用户的耐心被迅速消耗殆尽,关闭应用,转而选择了竞争对手的产品…...

信号调制与解调技术基础解析
调制解调技术是通信系统中实现基带信号与高频载波信号相互转换的主要技术,通过调整信号特性使其适应不同信道环境,保障信息传输的效率和可靠性。 调制与解调的基本概念 调制(Modulation) 将低频基带信号(如语音或数…...

[PTA]2025 CCCC-GPLT天梯赛 胖达的山头
来源:L2-055 胖达的山头-Pintia题意:给定 n n n 个事件的起始和终止时刻(以hh:mm:ss给出),求最多并行事件数。关键词:差分(签到,模板题)题解:将所有时刻转换为秒,当某事件开始1,结束则-1。按时…...

基于Spring Cloud 2023.0.x + Micrometer Tracing的分布式链路追踪详细解析
前言 在微服务架构中,复杂的调用链路常让问题排查如大海捞针。Spring Cloud 2023.0.x整合Micrometer Tracing,深度支持OpenTelemetry标准,为开发者提供了轻量、高效的分布式链路追踪能力。本文将深入解析从TraceID透传到可视化分析的全流程实现,结合最新技术栈代码…...
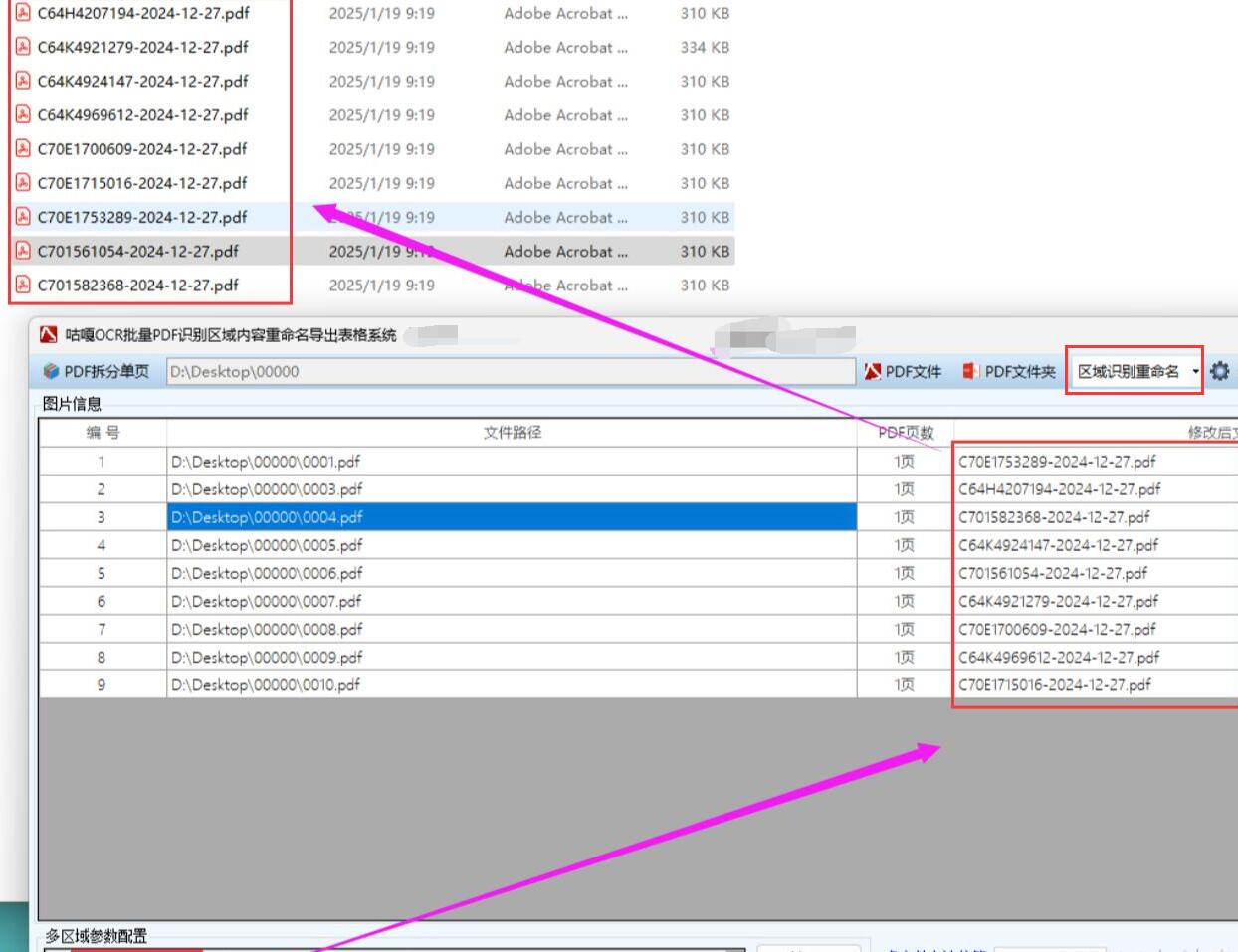
【扫描件批量改名】批量识别扫描件PDF指定区域内容,用识别的内容修改PDF文件名,基于C++和腾讯OCR的实现方案,超详细
批量识别扫描件PDF指定区域内容并重命名文件方案 应用场景 本方案适用于以下场景: 企业档案数字化管理:批量处理扫描的合同、发票等文件,按内容自动分类命名财务票据处理:自动识别票据上的关键信息(如发票号码、日期)用于归档医疗记录管理:从扫描的检查报告中提取患者I…...

LOH 怎么进行深度标准化?
The panel of normals is applied by replacing the germline read depth of the sample with the median read depth of samples with the same genotype in our panel. 1.解释: panel of normal 正常组织,用于识别技术噪音 germline read depth: 胚系测序深度。根…...

【Python Web开发】01-Socket网络编程01
文章目录 1.套接字(Socket)1.1 概念1.2 类型1.3 使用步骤 Python 的网络编程主要用于让不同的计算机或者程序之间进行数据交换和通信,就好像人与人之间打电话、发消息一样。 下面从几个关键方面通俗易懂地介绍一下: 1.套接字(Socket) 在 Python 网络编…...
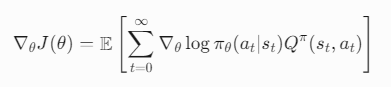
序列决策问题(Sequential Decision-Making Problem)
序列决策问题(Sequential Decision-Making Problem)是强化学习(Reinforcement Learning, RL)的核心研究内容,其核心思想是:智能体(Agent)需要在连续的时间步骤中,通过…...

