C语言对n进制的处理

先看一道题目:

从键盘获取一个正整数,如果把它转为16进制的数字,那么它是一个几位数呢?如果把它转为28进制又是一个几位数呢?

在讲这个题目之前,我们先要了解进制转换

什么是进制转换？
简单来说，进制就是数位的表示方法。

十进制（常用）是每逢10进1。

二进制是每逢2进1。

八进制是每逢8进1。

十六进制是每逢16进1。

而进制转换，就是把一个数从一种进制换到另一种进制表示。

比如：

十进制 10 转成二进制 = 1010

十进制 10 转成八进制 = 12

十进制 10 转成十六进制 = A

虽然数字代表的大小不变，但写法变了！

怎么进行进制转换？（超简单版）

1. 十进制 → 其他进制
方法：不断除目标进制，记录余数，最后倒着读。

比如：

十进制123转成8进制

123 ÷ 8 = 15 余 3

15 ÷ 8 = 1 余 7

1 ÷ 8 = 0 余 1

余数倒着读：1 7 3 → 八进制是173

2. 其他进制 → 十进制
方法：按照位数乘以进制的幂次方，加起来。

比如：

八进制173转回十进制

= 1×8² + 7×8¹ + 3×8⁰  //1在百位所以是平方,7在十位所以是1次方,类比十进制

= 1×64 + 7×8 + 3×1

= 64 + 56 + 3

= 123

这道题目求进制转化后的数字的位数,其实就是求进制转化过程中除的次数!

现在直接给出这道题目的代码:

int Fun1(int x,int n)//统计x转为n进制是个几位数
{int count = 0;//计数器while (x != 0){x /= n;count++;}return count;
}int main()
{printf("%d\n", Fun1(123, 10));//3printf("%d\n", Fun1(123, 16));//2printf("%d\n", Fun1(123, 8));//3printf("%d\n", Fun1(123, 2));//7printf("%d\n", Fun1(123, 28));return 0;
}

首先，看看函数 Fun1：

int Fun1(int x,int n)//统计x转为n进制是个几位数
{int count = 0;//计数器while (x != 0){x /= n;count++;}return count;
}

简单理解就是：

把数字 x 按 n 进制去表示，看看一共需要多少位。

每次 x /= n，就相当于“去掉”一位。

直到 x 变成0，统计了一共去过几次，就是它的位数。

再看 main 函数：

int main()
{printf("%d\n", Fun1(123, 10));//3printf("%d\n", Fun1(123, 16));//2printf("%d\n", Fun1(123, 8));//3printf("%d\n", Fun1(123, 2));//7printf("%d\n", Fun1(123, 28));return 0;
}

逐行解释一下输出：

Fun1(123, 10)：

123是十进制本身。

123 / 10 = 12

12 / 10 = 1

1 / 10 = 0 （结束）

总共除过3次，所以是3位。

Fun1(123, 16)：

123转16进制是 7B。

123 / 16 = 7

7 / 16 = 0

两次，所以是2位。

Fun1(123, 8)：

123转8进制是173。

123 / 8 = 15

15 / 8 = 1

1 / 8 = 0

三次，所以是3位。

Fun1(123, 2)：

123转二进制是1111011。

123 / 2 = 61

61 / 2 = 30

30 / 2 = 15

15 / 2 = 7

7 / 2 = 3

3 / 2 = 1

1 / 2 = 0

七次，所以是7位。

Fun1(123, 28)：

123 / 28 = 4

4 / 28 = 0

两次，所以是2位。

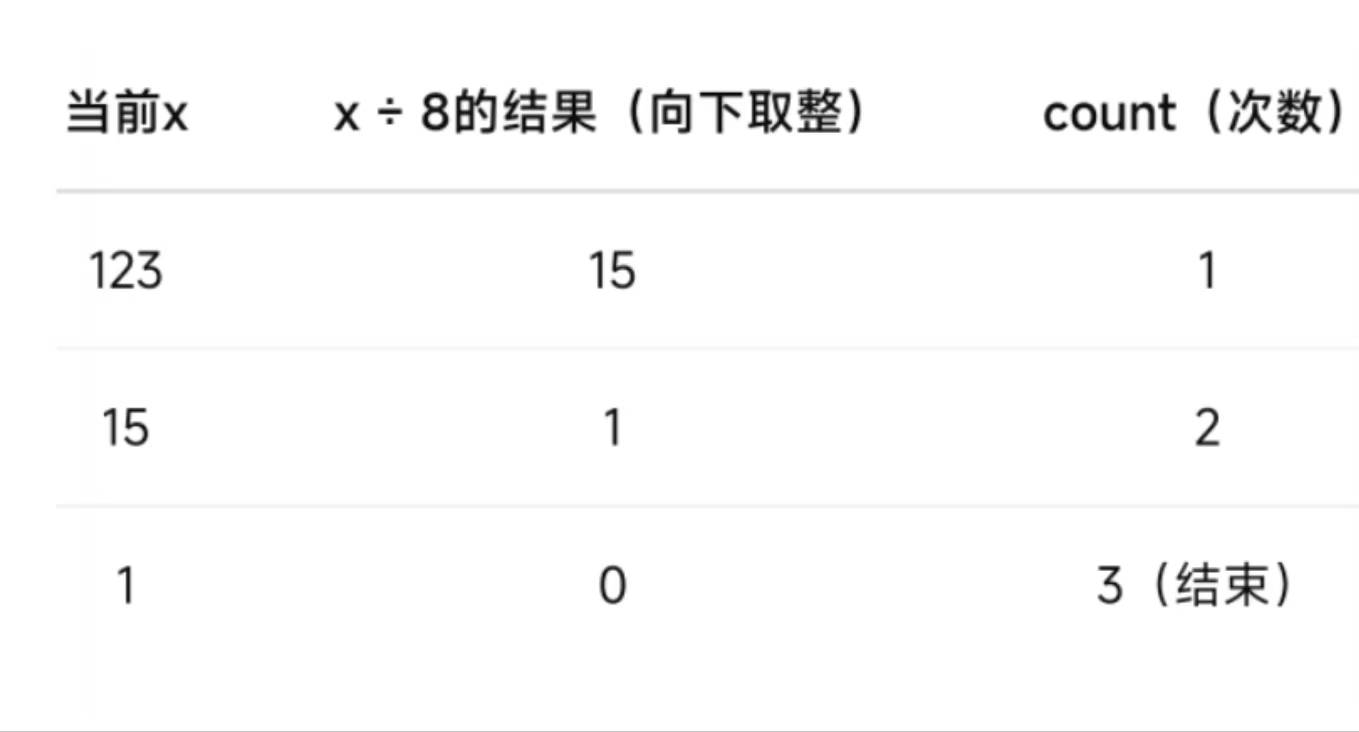
图示:以Fun1(123,8)为例

(也就是求123在8进制下是几位)

我们做的是不断除以8,来"去掉"低位:

(这道题目求进制转化后的数字的位数,其实就是求进制转化过程中除的次数!)

总结一句话：

Fun1(x, n) 实际上是 x在n进制下所需要的位数，
原理是每次除以n，把最低位"丢掉"，直到剩0，统计除的次数。

再看一题:

假设在n进制下，下面的等式成立，567*456=150216，n的值是（）。
A. 9 B. 10 C. 12 D.18

 

int main()
{for (int n = 9; n <= 18; n++)//进制{if ((5 * n * n + 6 * n + 7) * (4 * n * n + 5 * n + 6) ==((int)pow(n, 5) + 5 * (int)pow(n, 4) + 2 * n * n + n+6)){printf("%d\n",n);break;}}//int n = (int)pow(10,5);//(int):把后面的double强制转换为int//printf("%d\n",n);return 0;
}

逐步解释：

for (int n = 9; n <= 18; n++)

n从9开始，每次循环n++，直到n=18。

每次都检查一个条件，想找一个满足特定数学关系的n。

if ((5 * n * n + 6 * n + 7) * (4 * n * n + 5 * n + 6) ==((int)pow(n, 5) + 5 * (int)pow(n, 4) + 2 * n * n + n+6))

判断式的左边：

(5n² + 6n + 7) * (4n² + 5n + 6) 

判断式的右边：

n⁵ + 5n⁴ + 2n² + n + 6 

（注意：pow(n, 5)和pow(n, 4)是计算n的5次方、4次方，因为pow返回double类型，所以用(int)强制类型转换成整数。）

如果左边和右边的结果相等：

printf("%d\n", n); 输出这个n

break; 退出循环（因为已经找到了）。

整体意思总结：

在n从9到18的范围里，找一个n，使得 (5n² + 6n + 7)*(4n² + 5n + 6) 等于 n⁵ + 5n⁴ + 2n² + n + 6，并输出这个n。