【算法笔记】贪心算法
一、什么是贪心算法?
贪心算法是一种在每一步选择中都采取当前看起来最优(最“贪心”)的策略,从而希望得到全局最优解的算法设计思想。
- 核心思想:每一步都做出局部最优选择,不回退。
- 适用场景:问题具有最优子结构且满足贪心选择性质 —— 即局部最优可以导出全局最优。
二、贪心算法的典型流程
- 排序/预处理:对待选元素进行必要的排序或组织。
- 局部选择:按照某种规则(如最大收益、最小代价等)依次选取元素。
- 可行性检验:检查当前选择是否满足约束。
- 解的构造:在每次选择的基础上逐步构建最终解。
三、经典例题回顾
1. 活动选择问题
- 题目:有 n n n 个活动,每个活动有开始时间 s i s_i si 和结束时间 f i f_i fi,要求选出最多互不冲突的活动集合。
- 贪心策略:按活动结束时间从小到大排序,每次选取结束最早且与当前已选活动不冲突的活动。
2. 分数背包问题(Fractional Knapsack)
- 题目:有 n n n 件物品,每件物品重量 w i w_i wi,价值 v i v_i vi,背包容量 W W W。物品可分割装入。
- 贪心策略:按单位重量价值 v i w i \frac{v_i}{w_i} wivi 从大到小装入;装不下时装入尽可能多的部分。
3. 最小生成树(Kruskal 算法)
- 题目:给定带权无向图,求一棵权值之和最小的生成树。
- 贪心策略:对所有边按权值从小到大排序,依次加入不会形成环的最小边。
四、实战题目 —— 给 n n n 个国家加税
4.1 题目描述
- 有 n n n 个国家,初始关税税率均为 100%。
- 对第 i i i 个国家,加税一次可将其税率提升 p i % p_i\% pi%(即税率从上一次的值再加上 p i p_i pi 百分点)。
- 允许一共进行 k k k 次加税操作,每次只能选择一个国家进行一次加税。
- 求经过 k k k 次加税后,所有国家税率的累乘(乘积)的最大值。
示例
输入:n = 3, p = [2, 5, 3], k = 4
输出:最大乘积(按百分比计算)
4.2 贪心思路分析
收益定义
- 对第 i i i 个国家当前税率 t i t_i ti(最开始 t i = 100 % t_i=100\% ti=100%)再加一次 p i % p_i\% pi%,其新的税率为 t i + p i t_i + p_i ti+pi。
- 在乘积中,相当于将当前乘积乘以 t i + p i t i \frac{t_i + p_i}{t_i} titi+pi,因此这次操作对总乘积的放大倍数为:
r i = t i + p i t i = 1 + p i t i r_i = \frac{t_i + p_i}{t_i} = 1 + \frac{p_i}{t_i} ri=titi+pi=1+tipi
- 要使乘积最大,每次都应选择能带来最大放大倍数 r i r_i ri 的国家。
优先队列实现
- 使用一个最大堆(priority_queue)存储每个国家当前可获得的放大倍数 r i r_i ri。
- 每次取出堆顶( r i r_i ri 最大的国家),实施一次加税:
- 更新该国家税率: t i ← t i + p i t_i \leftarrow t_i + p_i ti←ti+pi。
- 计算新的放大倍数: r i ← 1 + p i t i r_i \leftarrow 1 + \frac{p_i}{t_i} ri←1+tipi。
- 将更新后的 r i r_i ri 重新压入堆中。
- 重复上述过程 k k k 次,结束后遍历所有国家税率,计算乘积。
4.3 代码示例(C++)
#include <bits/stdc++.h>
using namespace std;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, k;cin >> n >> k;vector<double> p(n), t(n, 100.0);for (int i = 0; i < n; i++) {cin >> p[i];}// 优先队列:pair<放大倍数, 国家索引>auto cmp = [](const pair<double,int>& a, const pair<double,int>& b) {return a.first < b.first;};priority_queue<pair<double,int>, vector<pair<double,int>>, decltype(cmp)> pq(cmp);// 初始化for (int i = 0; i < n; i++) {double r = 1.0 + p[i] / t[i];pq.push({r, i});}// 执行 k 次加税while (k--) {auto [r, i] = pq.top(); pq.pop();t[i] += p[i];r = 1.0 + p[i] / t[i];pq.push({r, i});}// 计算累乘结果double ans = 1.0;for (double tax : t) {ans *= tax / 100.0;}cout << fixed << setprecision(6) << ans << "\n";return 0;
}
4.4 复杂度分析
- 每次操作:弹出堆顶 + 插入堆顶,各 O ( log n ) O(\log n) O(logn)。
- 总共 k k k 次操作,时间复杂度为: O ( k log n ) O(k \log n) O(klogn)。
- 空间复杂度:需要存储 n n n 个国家的信息,为 O ( n ) O(n) O(n)。
五、更多贪心练习题推荐
- 区间染色问题:给定区间集合,最少使用多少种颜色使重叠区间不同色?
- 跳跃游戏 II:每格有最大跳跃长度,求最少跳跃次数到达末尾。
- 分配饼干:孩子有满足度,饼干有大小,如何让最多孩子满足?
- 连通区间合并:给一堆区间,合并所有重叠区间,输出不重叠区间集合。
六、小结
- 贪心算法以“当前最优选择”逐步构建解,适合于“最优子结构”且满足“贪心选择性质”的问题。
- 真正的难点在于如何证明局部最优能导出全局最优,以及如何设计合适的贪心策略。
- 通过上述“加税”题,以及经典例题的练习,可以加深对贪心算法的理解与应用。
相关文章:

【算法笔记】贪心算法
一、什么是贪心算法? 贪心算法是一种在每一步选择中都采取当前看起来最优(最“贪心”)的策略,从而希望得到全局最优解的算法设计思想。 核心思想:每一步都做出局部最优选择,不回退。适用场景:…...

Node.js 开发项目
初始化 npm init## npm install 编辑packege.json 添加,以支持ES6的语法 "type": "module" 连接mysql示例 import db from ./db/ops_mysql.jsconst createTable async () > {const insert_data CREATE TABLE IF NOT EXISTS users (…...

网络准入控制系统推荐:2025年构建企业网络安全的第一道防线
随着信息技术的飞速发展,企业网络环境日益复杂,阳途网络准入控制系统作为一种先进的网络安全解决方案,其核心是确保网络接入的安全性。 一、网络准入控制系统的基本原理与功能 网络准入控制以“只有合法的用户、安全的终端才可以接入网络”为…...
XSS跨站--订单和Shell箱子后门
本文主要内容 手法 XSS平台使用 XSS工具使用 XSS结合其他漏洞 XSS具体使用场景 某订单系统XSS盲打_平台 某Shell箱子系统XSS盲打_工具 [1]订单系统经典案例 第一个简易攻击流程(订单系统):通过平台完成XSS跨站之后&a…...

游戏遭遇DDoS攻击如何快速止损?实战防御策略与应急响应指南
是不是很抽象 我自己画的 一、游戏DDoS攻击特征深度解析 游戏行业DDoS攻击呈现复合型特征,2023年监测数据显示,针对游戏服务器的攻击中,63%采用UDP反射放大HTTP慢速攻击组合,攻击峰值达3.2Tbps。攻击者利用游戏协议特性ÿ…...

cocos creator使用jenkins打包流程,打包webmobile
windows电脑使用 如果你的电脑作为打包机,一定要锁定自己的ip,如果ip动态获取,可能后续会导致jenkins无法访问,还需要重新配置jenkins和http-server的端口 从jenkins官网下载windows版 Thank you for downloading Windows Stable installer 1.jenkins安…...
自动驾驶(ADAS)领域常用数据集介绍
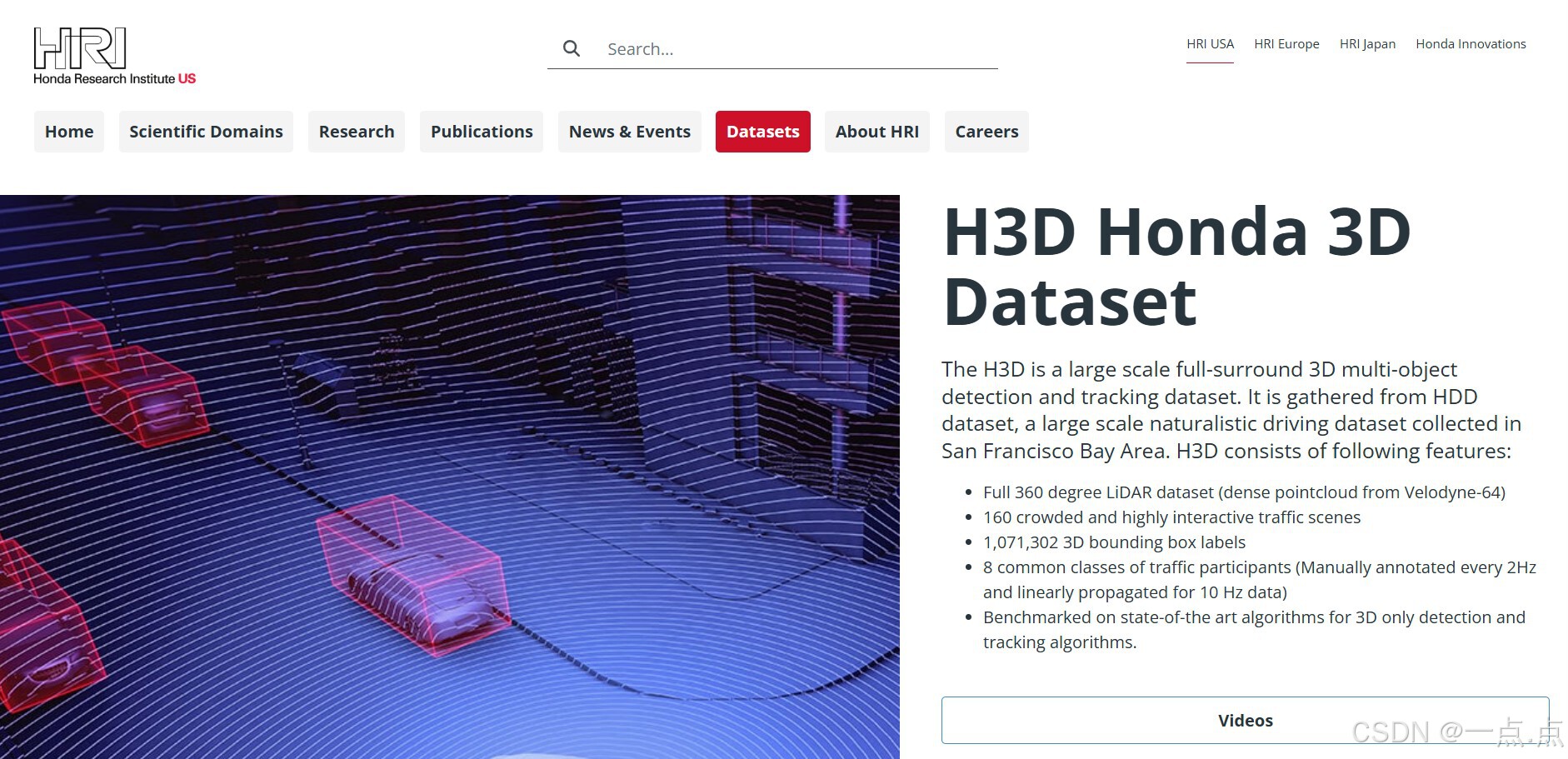
1. KITTI 数据集 简介:由德国卡尔斯鲁厄理工学院与丰田研究院联合创建,是自动驾驶领域最经典的评测基准,涵盖立体视觉、光流、3D检测等任务。包含市区、乡村和高速公路场景的真实数据,标注对象包括车辆、行人等,支持多…...

C++ 部署的性能优化方法
一、使用结构体提前存放常用变量 在编写前后处理函数时,通常会多次用到一些变量,比如模型输入 tensor 的 shape,count 等等,若在每个处理函数中都重复计算一次,会增加部署时的计算量。对于这种情况,可以考…...

关于IDEA的循环依赖问题
bug描述:(java: 模块循环不支持注解处理。请确保将循环 [...] 中的所有模块排除在注解处理之外) 解决方法:...

如何在idea中写spark程序
在 IntelliJ IDEA 中编写 Spark 程序,可按以下步骤进行: 1. 创建新项目 打开 IntelliJ IDEA,选择File -> New -> Project。在左侧面板选择Maven或者Gradle(这里以 Maven 为例),确保Project SDK选择…...

RAG工程-基于LangChain 实现 Advanced RAG(预检索优化)
Advanced RAG 概述 Advanced RAG 被誉为 RAG 的第二范式,它是在 Naive RAG 基础上发展起来的检索增强生成架构,旨在解决 Naive RAG 存在的一些问题,如召回率低、组装 prompt 时的冗余和重复以及灵活性不足等。它重点聚焦在检索增强࿰…...

关于常量指针和指向常量的指针
关于指针,对于常量指针和指向常量的指针也是傻傻分不清。看到定义时,不知道是指针不能变,还是指针指向的内容不能变量。 先看形式: const char * A; char * const B; 这两种有什么区别?傻傻分不清。 A这种定义&am…...

《Masked Autoencoders Are Scalable Vision Learners》---CV版的BERT
目录 一、与之前阅读文章的关系? 二、标题:带掩码的自auto编码器是一个可拓展的视觉学习器 三、摘要 四、核心图 五、结果图 六、不同mask比例对比图 七、“Introduction” (He 等, 2021, p. 1) 引言 八、“Related Work” (He 等, 2021, p. 3)相…...

高压直流输电MATLAB/simulink仿真模型+说明文档
1.模型简介 本仿真模型基于MATLAB/Simulink(版本MATLAB 2018Ra)软件。建议采用matlab2018 Ra及以上版本打开。(若需要其他版本可联系代为转换) 使用一个传输功率为1000MW(500 kV,2 kA)直流互连…...

locust压力测试
安装 pip install locust验证是否安装成功 locust -V使用 网上的教程基本上是前几年的,locust已经更新了好几个版本,有点过时了,在此做一个总结 启动 默认是使用浏览器进行设置的 # 使用浏览器 locust -f .\main.py其他参数 Usage: locust […...

python 线程池顺序执行
在Python中,线程池(ThreadPoolExecutor)默认是并发执行任务的,但若需要实现任务的顺序执行(按提交顺序执行或按结果顺序处理),可以通过以下方案实现: 方案一:强制单线程&…...

第十二届蓝桥杯 2021 C/C++组 空间
目录 题目: 题目描述: 题目链接: 思路: 思路详解: 代码: 代码详解: 题目: 题目描述: 题目链接: 空间 - 蓝桥云课 思路: 思路详解&#…...

以太网的mac帧格式
一.以太网的mac帧 帧的要求 1.长度 2.物理层...

前端如何使用Mock模拟数据实现前后端并行开发,提升项目整体效率
1. 安装 Mock.js npm install mockjs --save-dev # 或使用 CDN <script src"https://cdn.bootcdn.net/ajax/libs/Mock.js/1.0.0/mock-min.js"></script>2. 创建 Mock 数据文件 在项目中新建 mock 目录,创建 mock.js 文件: // m…...

【hadoop】HBase shell 操作
1.创建course表 hbase(main):002:0> create course,cf 2.查看HBase所有表 hbase(main):003:0> list 3.查看course表结构 hbase(main):004:0> describe course 4.向course表插入数据 hbase(main):005:0> put course,001,cf:cname,hbase hbase(main):006:0> …...

如何使用 Redis 缓存验证码
目录 🧠 Redis 缓存验证码的工作原理 🧰 实现流程 1. 安装 Redis 和 Python 客户端 2. 生成并缓存验证码 示例代码:生成并存储验证码 3. 发送验证码(以短信为例) 4. 校验验证码 示例代码:校验验证码…...

深度学习---框架流程
核心六步 一、数据准备 二、模型构建 三、模型训练 四、模型验证 五、模型优化 六、模型推理 一、数据准备:深度学习的基石 数据是模型的“燃料”,其质量直接决定模型上限。核心步骤包括: 1. 数据收集与标注 来源:公开数据集…...

业绩回暖、股价承压,三只松鼠赴港上市能否重构价值锚点?
在营收重返百亿俱乐部后,三只松鼠再度向资本市场发起冲击。 4月25日,这家坚果零食巨头正式向港交所递交上市申请书,若成功登陆港股,将成为国内首个实现“AH”双上市的零食品牌。 其赴港背后的支撑力,显然来自近期披露…...

JAVA-StringBuilder使用方法
JAVA-StringBuilder使用方法 常用方法 append(Object obj) 追加内容到末尾 sb.append(" World"); insert(int offset, Object obj) 在指定位置插入内容 sb.insert(5, “Java”); delete(int start, int end) 删除指定范围的字符 sb.delete(0, 5); replace(int start…...

【Python】Matplotlib:立体永生花绘制
本文代码部分实现参考自CSDN博客:https://blog.csdn.net/ak_bingbing/article/details/135852038 一、引言 Matplotlib作为Python生态中最著名的可视化库,其三维绘图功能可以创造出令人惊叹的数学艺术。本文将通过一个独特的参数方程,结合极…...

Unity AI-使用Ollama本地大语言模型运行框架运行本地Deepseek等模型实现聊天对话(一)
一、Ollama介绍 官方网页:Ollama官方网址 中文文档参考:Ollama中文文档 相关教程:Ollama教程 Ollama 是一个开源的工具,旨在简化大型语言模型(LLM)在本地计算机上的运行和管理。它允许用户无需复杂的配置…...

terraform使用vault动态管多理云账号AK/SK
为了使用 Terraform 和 HashiCorp Vault 动态管理多个云账号的 Access Key (AK) 和 Secret Key (SK),可以按照以下步骤实现安全、自动化的凭证管理: 一、架构概述 核心组件: Vault:存储或动态生成云账号的 AK/SK,提供…...

SAP /SDF/SMON配置错误会导致HANA OOM以及Disk Full的情况
一般来说,为了保障每日信息收集,每个企业都会配置/SDF/SMON的监控。这样在出现性能问题时,可以通过收集到的snapshot进行分析检查。如果/SDF/SMON在配置时选取了过多的记录项,或者选择了过低的时间间隔[Interval in seconds],那显…...

CMU和苹果公司合作研究机器人长序列操作任务,提出ManipGen
我们今天来介绍一项完成Long-horizon任务的一项新的技术:ManipGen。 什么叫Long-horizon?就是任务比较长。说到底,也是任务比较复杂。 那么这个技术就给我们提供了一个非常好的解决这类问题的思路,同时,也取得了不错的…...
大模型(LLMs)强化学习—— PPO
一、大语言模型RLHF中的PPO主要分哪些步骤? 二、举例描述一下 大语言模型的RLHF? 三、大语言模型RLHF 采样篇 什么是 PPO 中 采样过程?介绍一下 PPO 中 采样策略?PPO 中 采样策略中,如何评估“收益”? …...
