【官方题解】StarryCoding 入门教育赛 2 | acm | 蓝桥杯 | 新手入门
本场比赛开始时题面存在一些问题,私密马赛!
A.池化【入门教育赛】
根据题目所给公式计算即可。
#include "bits/stdc++.h"signed main() {int t; std::cin >> t;while (t --) {int l, k, s, p; std::cin >> l >> k >> s >> p;int ans = floor((l + 2 * p - k) / s) + 1;std::cout << ans << "\n";}
}
B. 牢e买黄金【入门教育赛】
枚举卖点 i i i,那么仅需找到数组 a a a的区间 [ 1 , i − 1 ] [1, i - 1] [1,i−1]的最小值,维护一个前缀最值即可。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 9;
using ll = long long;
ll a[N];int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);ll n, x;cin >> n >> x;for(int i = 1;i <= n;++ i)cin >> a[i];ll mi = a[1], ans = 0;for(int i = 1;i <= n; ++ i){ans = max(ans, a[i] - mi);mi = min(mi, a[i]);}cout << ans * x << '\n';return 0;
}
C.前缀序列【入门教育赛】
思维题,我们从右往左考虑,对于 i i i,若 a i a_i ai为负数,就直接将其取相反数就好了,至多 n n n次一定可以使得所有元素为非负整数,所以答案就是所有元素的绝对值之和。
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 9;
using ll = long long;
ll a[N];int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);ll n;cin >> n;for(int i = 1;i <= n;++ i)cin >> a[i];ll ans = 0;for(int i = 1;i <= n; ++ i)ans += (a[i] < 0 ? -a[i] : a[i]);cout << ans << '\n';return 0;
}
D.相邻最大公约数【入门教育赛】
动态规划,定义状态 d p [ i ] [ j ] dp[i][j] dp[i][j]表示 a i a_i ai是否增加 x x x(若 j = 0 j=0 j=0则没加 x x x,反之则加了)的情况下区间 [ 1 , i ] [1, i] [1,i]相邻 g c d gcd gcd之和。
d p [ i ] [ 0 ] dp[i][0] dp[i][0]可以从 d p [ i − 1 ] [ 0 ] dp[i - 1][0] dp[i−1][0]和 d p [ i − 1 ] [ 1 ] dp[i - 1][1] dp[i−1][1]转移过来, d p [ i ] [ 1 ] dp[i][1] dp[i][1]亦同。
状态转移方程请见代码,注意从 2 2 2开始转移。
#include <bits/stdc++.h>
using namespace std;using ll = long long;
const int N = 1e5 + 9;
ll dp[N][2], a[N];ll gcd(ll a, ll b){return b == 0 ? a : gcd(b, a % b);
}int main(){ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);ll n, x;cin >> n >> x;for(int i = 1;i <= n; ++ i)cin >> a[i];for(int i = 2;i <= n; ++ i){dp[i][0] = max(dp[i - 1][0] + gcd(a[i - 1], a[i]), dp[i - 1][1] + gcd(a[i - 1] + x, a[i]));dp[i][1] = max(dp[i - 1][0] + gcd(a[i - 1], a[i] + x), dp[i - 1][1] + gcd(a[i - 1] + x, a[i] + x));}cout << max(dp[n][0], dp[n][1]) << '\n';
}
E.基环树【入门教育赛】
基环树找环模板题,可用dfs或拓扑排序完成。
dfs解法:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 9;
ll a[N], n;
vector<int> g[N];
bitset<N> vis;
stack<int> stk;
ll ans;bool dfs(int x, int fa){vis[x] = true;stk.push(x);for(const auto &y : g[x]){if(y == fa)continue;if(vis[y]){while(stk.size()){int t = stk.top();stk.pop();ans += a[t];if(t == y)break;}return true;}if(dfs(y, x))return true;}stk.pop();return false;
}int main()
{cin >> n;for(int i = 1;i <= n; ++ i)cin >> a[i];for(int i = 1;i <= n; ++ i){int x, y;cin >> x >> y;if(x == y){cout << a[x] << '\n';return 0;}g[x].push_back(y), g[y].push_back(x);}if(n <= 2){ll ans = 0;for(int i = 1;i <= n; ++ i)ans += a[i];cout << ans << '\n';return 0;}dfs(1, 0);cout << ans << '\n';return 0;
}
拓扑排序做法:
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e5 + 9;
ll a[N], ind[N], n;
vector<int> g[N];void topo(){queue<int> q;for(int i = 1;i <= n; ++ i){if(ind[i] == 1)q.push(i);}while(q.size()){int x = q.front();q.pop();for(const auto &y : g[x]){if(-- ind[y] == 1)q.push(y);}}
}int main()
{cin >> n;for(int i = 1;i <= n; ++ i)cin >> a[i];set<pair<int, int> > st;for(int i = 1;i <= n; ++ i){int x, y;cin >> x >> y;if(x == y){cout << a[x] << '\n';return 0;}g[x].push_back(y), g[y].push_back(x);ind[x] ++, ind[y] ++;}if(n <= 2){ll ans = 0;for(int i = 1;i <= n; ++ i)ans += a[i];cout << ans << '\n';return 0;}topo();ll ans = 0;for(int i = 1;i <= n; ++ i)if(ind[i] == 2)ans += a[i];cout << ans << '\n';return 0;
}
相关文章:

【官方题解】StarryCoding 入门教育赛 2 | acm | 蓝桥杯 | 新手入门
比赛传送门: 本场比赛开始时题面存在一些问题,私密马赛! A.池化【入门教育赛】 根据题目所给公式计算即可。 #include "bits/stdc.h"signed main() {int t; std::cin >> t;while (t --) {int l, k, s, p; std::cin >&…...
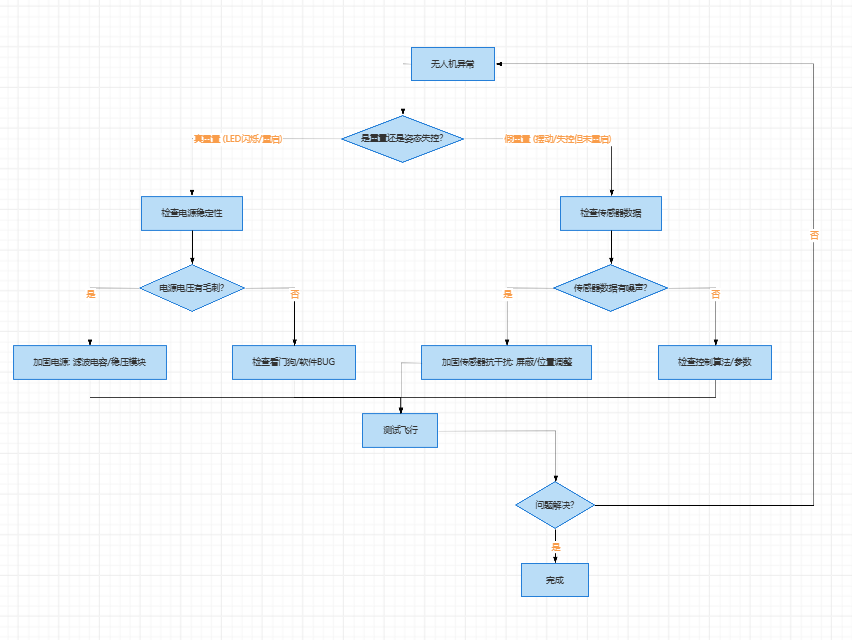
无人机相关技术与故障排除笔记
无人机相关技术与故障排除笔记 本文档整理了关于无人机电调、电机、通信协议、传感器以及硬件故障排除相关的笔记和解释。 1. 电调 (ESC) PWM 输出初始化设置 初始化电调(电子调速器)的 PWM 输出功能时,设置 频率 400Hz、分辨率 10000、初…...

SpringSecurity(自定义异常处理)
文末有本篇文章的项目源码可供下载学习。 在实际的项目开发过程中,我们对于认证失败或者授权失败需要像接口一样返回相同结构的json数据,这样可以让前端对响应进行统一的处理。要实现这个功能我们需要知道SpringSecurity的异常处理机制。 在SpringSecu…...

Java——反射
目录 5 反射 5 反射 类信息:方法、变量、构造器、继承和实现的类或接口。反射:反射是 Java 中一项强大的特性,它赋予了程序在运行时动态获取类的信息,并能够调用类的方法、访问类的字段以及操作构造函数等的能力。通过反射&#…...

本地玩AI绘画 | StableDiffusion安装到绘画
环境须知 Cuda必须安装 不需要安装Python,因为该项目会自动安装Python3.10的虚拟环境 1.下载StableDiffusionWebUI压缩包并解压 下载方式一: 从Github下载https://github.com/AUTOMATIC1111/stable-diffusion-webui 的压缩包,解压后名为…...

C++:书架
【描述】 John最近买了一个书架用来存放奶牛养殖书籍,但书架很快被存满了,只剩最顶层有空余。 John共有N头奶牛(1 ≤ N ≤ 20,000),每头奶牛有自己的高度Hi(1 ≤ Hi ≤ 10,000),N头奶牛的总高度为S。书架高度为B(1 ≤ B ≤ S <…...

project从入门到精通(四)
目录 日程表的设置和妙用 为日程表视图添加任务 用日程表视图的好处 编辑 查找任务的前置任务和后续任务 方法1:采用复合视图的方式 方法3:关系图法 方法4:通过任务路径的方式检查所选任务的前置任务 前置任务和驱动前置任务的区…...

git项目迁移,包括所有的提交记录和分支 gitlab迁移到gitblit
之前git都是全新项目上传,没有迁移过,因为迁移的话要考虑已有项目上的分支都要迁移过去,提交记录能迁移就好;分支如果按照全新项目上传的方式需要新git手动创建好老git已有分支,在手动一个一个克隆老项目分支代码依次提…...

基于STM32、HAL库的SST26VF064B NOR FLASH存储器驱动应用程序设计
一、简介: SST26VF064B是Microchip公司生产的一款64Mbit(8MB)串行闪存器件,采用SPI接口通信,具有以下特点: 工作电压:2.7-3.6V 最高104MHz时钟频率 统一4KB扇区结构 快速擦除和编程时间 低功耗特性 支持标准SPI、Dual SPI和Quad SPI模式 二、硬件接口: STM32L4引脚SST26V…...

【黑马JavaWeb+AI知识梳理】后端Web基础01 - Maven
Maven Maven核心 Maven概述 定义: Maven是一款用于管理和构建Java项目的工具,是apache旗下的一个开源项目,基于项目对象模型(POM,project object model)的概念,通过一小段描述信息来管理项目的…...

港大今年开源了哪些SLAM算法?
过去的5个月,香港大学 MaRS 实验室陆续开源了四套面向无人机的在线 SLAM 框架:**FAST-LIVO2 、Point-LIO(grid-map 分支) 、Voxel-SLAM 、Swarm-LIO2 **。这四套框架覆盖了单机三传感器融合、高带宽高速机动、长时间多级地图优化以…...
)
Spring框架(1)
Spring框架是Java企业级开发中最受欢迎的框架之一,它通过简化开发流程、降低耦合度,让开发者能够更专注于业务逻辑的实现。本文将带你了解Spring框架的核心概念和基本用法。 一、Spring框架简介 Spring是一个轻量级的开源Java开发框架,由Ro…...

边缘计算:技术概念与应用详解
引言 随着物联网(IoT)、5G 和人工智能(AI)的快速发展,传统的云计算架构在处理海量数据和实时计算需求时逐渐显现出瓶颈。边缘计算(Edge Computing)作为一种新兴的计算范式,通过将计…...

Godot4.3类星露谷游戏开发之【昼夜循环】
千里之行,始于足下 文章目录 零、 笔记一、创造时间二、产生颜色三、搭建测试环境四、测试五、免费开源资产包 零、 笔记 为了让游戏可以拥有白天和黑夜,我们需要像上帝一样,在游戏中创造时间的规则,并在不同的时间点产生不同的颜…...
★★★★★)
数据结构每日一题day17(链表)★★★★★
题目描述:假设有两个按元素值递增次排列的线性表,均以单链表形式存储。请编与算法将这两个单链表归并为一个按元素值依次递减排列的单链表,并要求利用原来两个单链表的结点存放归并后的单链表。 算法思想: 1.初始化: 创建一个新…...

深入解析多线程与多进程:从理论到Python实践
一、并发编程的核心概念 1.1 多线程的本质与实现原理 多线程(Multithreading)是指在一个进程内创建多个执行流,共享同一进程资源(如内存空间、文件句柄等)的编程模型。其核心特征包括: 资源共享…...

当当网Top500书籍信息爬取与分析
爬取当当网的Top500书籍信息,并对书籍的评价数量进行排序,然后绘制前十名的条形图,然后对各个出版社出版的书籍数量进行排序,绘制百分比的饼图 # 导入所需的模块 import re # 正则表达式模块,用于提取文本中的特定模…...

Android Framework 记录之二
23、services目录 文件描述class AlarmManagerService extends IAlarmManager.Stub {//定时管理服务public class AppOpsService extends IAppOpsService.Stub { // 程序选项服务public class AppsLaunchFailureReceiver extends BroadcastReceiver { //app启动失败广播class A…...

RabbitMQ 幂等性与消息可靠性保障
一、引言 RabbitMQ 是一个广泛应用于软件开发、数据传输、微服务等领域的高效、可靠的开源消息队列系统1。在分布式系统中,保证消息的可靠传递和幂等性是至关重要的,它能够确保系统在各种复杂情况下的稳定性和数据的准确性。 二、消息可靠性保障 &…...

neo4j图数据库基本概念和向量使用
一.节点 1.新建节点 create (n:GroupProduct {name:都邦高保额团意险,description: "保险产品名称"} ) return n CREATE:Neo4j 的关键字,用于创建新节点或关系。 (n:GroupProduct): n 是节点的临时别名(变量名&#…...

修复笔记:获取 torch._dynamo 的详细日志信息
一、问题描述 在运行项目时,遇到与 torch._dynamo 相关的报错,并且希望获取更详细的日志信息以便于进一步诊断问题。 二、相关环境变量设置 通过设置环境变量,可以获得更详细的日志信息: set TORCH_LOGSdynamo set TORCHDYNAM…...

Windows平台下的Qt发布版程序打包成exe可执行文件(带图标)|Qt|C++
首先先找一个可执行文件的图标 可以去阿里的矢量图库里找 iconfont-阿里巴巴矢量图标库 找到想要的图标下载下来 此时的图标是png格式的,我们要转到icon格式的文件 要使用到一个工具Drop Icons_2.1.1.rar - 蓝奏云 生成icon文件后把icon文件放到你项目的根目录下…...

PDF解析新范式:Free2AI工具实测
在数字化浪潮中,PDF文件已成为企业、政府及个人存储与传递信息的核心载体。然而,PDF内容的提取与处理始终是行业痛点——无论是合同解析、研究报告整理,还是大规模知识库构建,传统方法常面临效率低、成本高、准确率不足等问题。Free2AI基于智能体技术与大模型算力,为PDF内…...

CSS--图片链接垂直居中展示的方法
原文网址:CSS--图片链接垂直居中展示的方法-CSDN博客 简介 本文介绍CSS图片链接垂直居中展示的方法。 图片链接 问题复现 源码 <html xml:lang"cn" lang"cn"><head><meta http-equiv"Content-Type" content&quo…...

聊聊Spring AI autoconfigure模块的拆分
序 本文主要研究一下Spring AI autoconfigure模块的拆分 v1.0.0-M6版本 (base) ➜ spring-ai-spring-boot-autoconfigure git:(v1.0.0-M6) tree -L 9 . ├── pom.xml ├── src │ ├── main │ │ ├── java │ │ │ └── org │ │ │ └…...

【Elastsearch】如何获取已创建的api keys
『这种方法其实无法获取秘钥,只是获取了秘钥的名字等信息』 在Elasticsearch中,可以通过API获取已创建的API密钥(API keys)。以下是具体步骤和示例: 1.使用GET请求获取API密钥 Elasticsearch提供了GETAPI,用…...

Flutter异步原理-Future
前言 在 Dart 中,谈到异步就离不开 Future。无论是 .then()、还是 await,它们背后运作的都是一个私有实现类:_Future ,我们平时使用的 Future 只是一个抽象接口,其真正的实现逻辑由_Future 承担。 class _Future<…...

TRAE 配置blender MCP AI自动3D建模
BlenderMCP - Blender模型上下文协议集成 BlenderMCP通过模型上下文协议(MCP)将Blender连接到Claude AI,允许Claude直接与Blender交互并控制Blender。这种集成实现了即时辅助的3D建模、场景创建和操纵。 1.第一步下载 MCP插件(addon.py):Blender插件,在…...

VUE2课程计划表练习
主要练习数据变量对象 以下是修正后的完整代码: //javascript export default {data() {return {list: [{ id: 1, subject: Vue.js 前端实战开发, content: 学习指令,例如 v-if、v-for、v-model 等, place: 自习室, status: false }// 可以在这里添加更…...

虚拟文件系统
虚拟文件系统(Virtual File System,VFS)是操作系统内核中的一个抽象层,它为不同的文件系统(如ext4、NTFS、FAT32等)提供统一的访问接口。通过VFS,用户和应用程序无需关心底层文件系统的具体差异…...
