vue配置代理解决前端跨域的问题

---

一、概述

跨域是指由于浏览器的同源策略限制，向不同源(不同协议、不同域名、不同端口)发送ajax请求会失败

二、报错现象

三、通过配置代理来解决

修改request.js中的baseURL为/api

在vite.config.js中增加代理配置

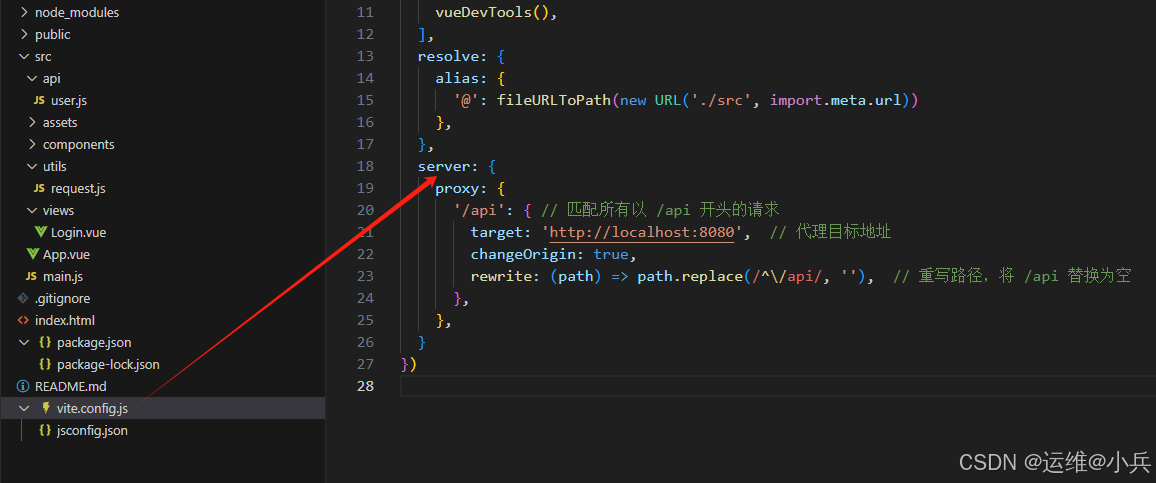
完整内容：

import { fileURLToPath, URL } from 'node:url'import { defineConfig } from 'vite'
import vue from '@vitejs/plugin-vue'
import vueDevTools from 'vite-plugin-vue-devtools'// https://vite.dev/config/
export default defineConfig({plugins: [vue(),vueDevTools(),],resolve: {alias: {'@': fileURLToPath(new URL('./src', import.meta.url))},},server: {proxy: {'/api': { // 匹配所有以 /api 开头的请求target: 'http://localhost:8080',  // 代理目标地址changeOrigin: true,rewrite: (path) => path.replace(/^\/api/, ''),  // 重写路径，将 /api 替换为空},},}
})

四、参考资料

https://www.bilibili.com/video/BV14z4y1N7pg?spm_id_from=333.788.player.switch&vd_source=0467ab39cc5ec5940fee22a0e7797575&p=73