每日c/c++题 备战蓝桥杯(P1002 [NOIP 2002 普及组] 过河卒)
洛谷P1002 [NOIP 2002 普及组] 过河卒 题解
题目描述
过河卒是一道经典的动态规划题目。题目大意是:一个卒子从棋盘左上角(0,0)出发,要走到右下角(n,m),棋盘上有一个马在(x,y)位置,卒子不能经过马所在位置及其周围8个位置。求卒子的合法路径总数。
解题思路
1. 问题分析
- 棋盘范围:棋盘为(n+1)×(m+1)的网格(坐标从0开始)
- 移动规则:卒子只能向右或向下移动
- 阻挡条件:马的位置及其控制的8个位置不可达
- 核心目标:统计从起点到终点的所有合法路径数
2. 动态规划建模
状态定义
dp[i][j]表示从起点(0,0)到达坐标(i,j)的合法路径总数
状态转移
d p [ i ] [ j ] = { 0 当前位置被马控制 1 i=0且j=0(起点) d p [ i − 1 ] [ j ] + d p [ i ] [ j − 1 ] 其他情况 dp[i][j] = \begin{cases} 0 & \text{当前位置被马控制} \\ 1 & \text{i=0且j=0(起点)} \\ dp[i-1][j] + dp[i][j-1] & \text{其他情况} \end{cases} dp[i][j]=⎩ ⎨ ⎧01dp[i−1][j]+dp[i][j−1]当前位置被马控制i=0且j=0(起点)其他情况
初始化条件
dp[0][0] = 1(起点自身算1条路径)- 被马控制的位置及其后续位置保持0值
3. 关键优化
坐标系偏移
将原始坐标系整体右移2格,下移2格(代码中b1 += 2; b2 += 2),目的是:
- 避免处理负数坐标
- 统一处理棋盘边界(通过循环条件
i <= b1和j <= b2自动限制范围)
马控制范围判断
通过预定义的8个方向向量:
int dx[8] = {-2,-2,-1,+1,+2,+2,+1,-1};
int dy[8] = {-1,+1,+2,+2,+1,-1,-2,-2};
检查目标位置是否被马控制:
bool pd(int a, int b) {// 检查马本体位置if (m1 == a && m2 == b) return false;// 检查8个控制位for (int i = 0; i < 8; ++i) {if (m1 + dx[i] == a && m2 + dy[i] == b) return false;}return true;
}
代码解析
1. 输入处理
cin >> b1 >> b2 >> m1 >> m2;
b1 += 2; // 扩展后的棋盘行数
b2 += 2; // 扩展后的棋盘列数
m1 += 2; // 马坐标同步偏移
m2 += 2;
2. 动态规划核心
for (int i = 2; i <= b1; ++i) { // 遍历所有行for (int j = 2; j <= b2; ++j) { // 遍历所有列if (!pd(i, j)) { // 被马控制的位置dp[i][j] = 0;continue;}if (i == 2 && j == 2) { // 起点初始化dp[i][j] = 1;continue;}dp[i][j] = dp[i-1][j] + dp[i][j-1]; // 状态转移}
}
3. 输出结果
最终结果存储在dp[b1][b2]中,直接输出即可。
复杂度分析
- 时间复杂度:O(nm),仅需遍历棋盘一次
- 空间复杂度:O(nm),使用二维数组存储状态
常见错误及注意事项
- 坐标偏移:忘记对马的位置进行同步偏移会导致控制范围判断错误
- 边界条件:当马位于起点或终点时,路径数应为0
- 数据类型:路径数可能超过int范围,需使用long long类型
- 初始化顺序:必须按行优先顺序填充dp数组,保证状态转移的正确性
扩展思考
- 记忆化搜索:可用DFS+记忆化实现,但时间复杂度较高(O(2^(n+m)))
- 矩阵快速幂:对于无阻挡的纯路径计数问题,可用组合数学优化到O(log(n+m))
- 三维DP:当需要记录更多状态时(如不同移动方式),可扩展DP维度
总结
本题通过动态规划完美解决了路径计数问题,关键点在于:
- 合理建模状态转移方程
- 正确处理棋盘边界和阻挡条件
- 通过坐标偏移简化边界判断
该方法的时间复杂度稳定在O(nm),能够高效处理题目给定的数据范围(n,m ≤ 20),是典型的动态规划应用案例。
相关文章:
)
每日c/c++题 备战蓝桥杯(P1002 [NOIP 2002 普及组] 过河卒)
洛谷P1002 [NOIP 2002 普及组] 过河卒 题解 题目描述 过河卒是一道经典的动态规划题目。题目大意是:一个卒子从棋盘左上角(0,0)出发,要走到右下角(n,m),棋盘上有一个马在(x,y)位置,卒子不能经过马所在位置及其周围8个位置。求卒…...
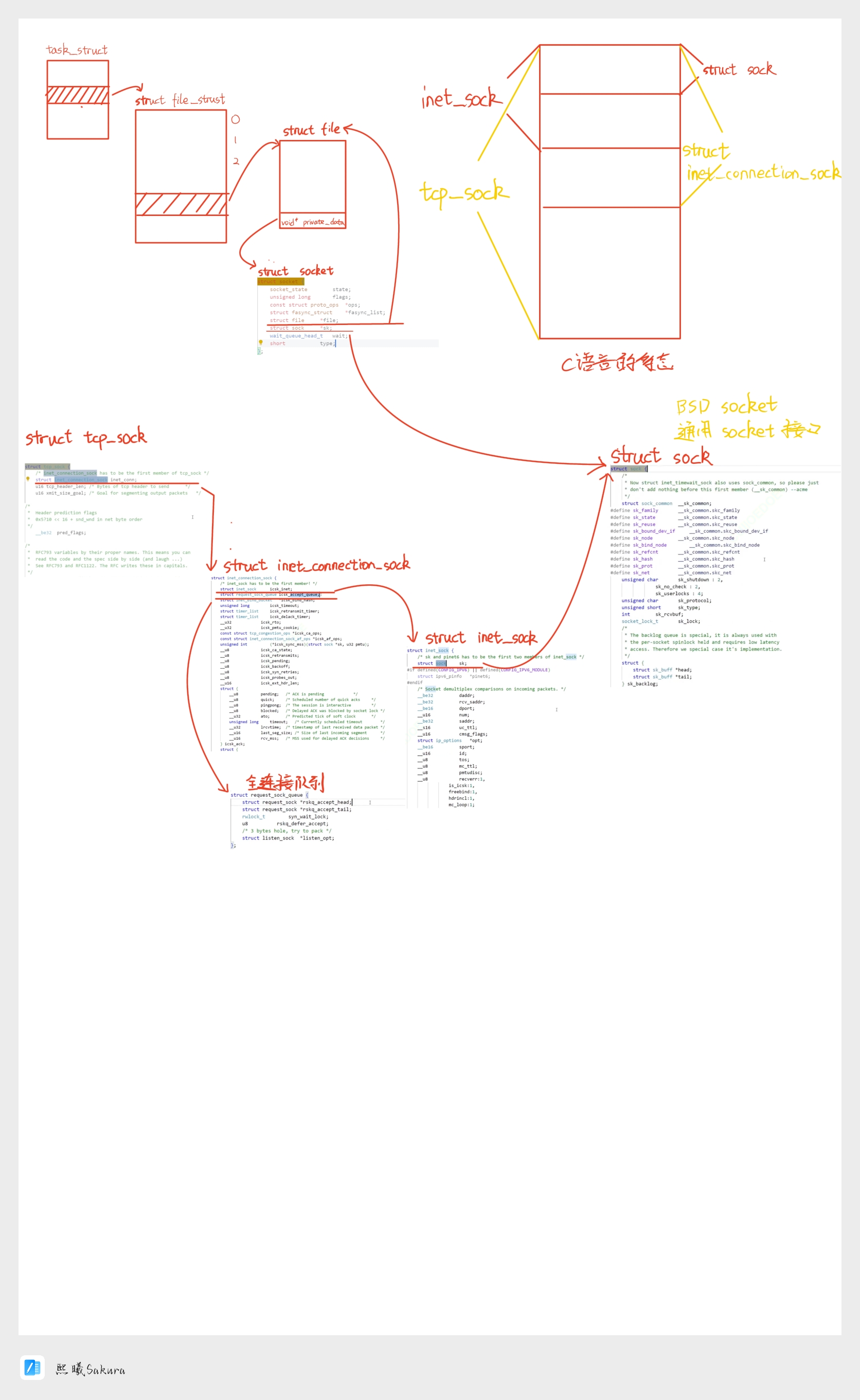
【Linux网络】TCP全连接队列
TCP 相关实验 理解 listen 的第二个参数 基于刚才封装的 TcpSocket 实现以下测试代码对于服务器, listen 的第二个参数设置为 1, 并且不调用 accept测试代码链接 test_server.cc #include "tcp_socket.hpp"int main(int argc, char* argv[]) {if (argc ! 3) {pri…...
HTML 颜色全解析:从命名规则到 RGBA/HSL 值,附透明度设置与场景应用指南
一、HTML 颜色系统详解 HTML 中的颜色可以通过多种方式定义,包括颜色名称、RGB 值、十六进制值、HSL 值等,同时支持透明度调整。以下是详细分类及应用场景: 1. 颜色名称(预定义关键字) HTML 预定义了 140 个标准颜色名…...

蓝桥杯12届国B 完全日期
题目描述。 如果一个日期中年月日的各位数字之和是完全平方数,则称为一个完全日期。 例如:2021 年 6 月 5 日的各位数字之和为 20216516,而 16 是一个完全平方数,它是 4 的平方。所以 2021 年 6 月 5 日是一个完全日期。 例如&…...

深度剖析多模态大模型中的视频编码器算法
写在前面 随着多模态大型语言模型(MLLM)的兴起,AI 理解世界的能力从静态的文本和图像,进一步拓展到了动态的、包含丰富时空信息的视频。视频作为一种承载了动作、交互、场景变化和声音(虽然本文主要聚焦视觉部分)的复杂数据形式,为 MLLM 提供了理解真实世界动态和因果关…...

游戏引擎学习第282天:Z轴移动与摄像机运动
运行游戏,展示目前进展 我们目前正在进行一个游戏开发项目。昨天,我们实现了基于房间的角色移动系统,并且加入了摄像机的跟随滚动功能。这是我们首次进入“游戏逻辑设计”阶段,也就是说,我们开始构建游戏本身的行为和…...

C++中的std::allocator
C中的std::allocator 文章目录 C中的std::allocator1.std::allocator1.1C中的placement new 和operator new1.2一个custom allocator的实现1.3使用std::allocator_traits实现allocator 1.std::allocator C中的std::allocator默默工作在CSTL中的所有容器的内存分配上࿰…...

Git/GitLab日常使用的命令指南来了!
在 GitLab 中拉取并合并代码的常见流程是通过 Git 命令来完成的。以下是一个标准的 Git 工作流,适用于从远程仓库(如 GitLab)拉取代码、切换分支、合并更新等操作。 🌐 一、基础命令:拉取最新代码 # 拉取远程仓库的所…...
aws 实践创建policy + Role
今天Cyber 通过image 来创建EC2 的时候,要添加policy, 虽然是administrator 的role, 参考Cyber 提供的link: Imageshttps://docs.cyberark.com/pam-self-hosted/14.2/en/content/pas%20cloud/images.htm#Bring 1 Step1:...
)
[Java实战]Spring Boot 解决跨域问题(十四)
[Java实战]Spring Boot 解决跨域问题(十四) 一、CORS 问题背景 什么是跨域问题? 当浏览器通过 JavaScript 发起跨域请求(不同协议、域名、端口)时,会触发同源策略限制,导致请求被拦截。 示例场…...

【HarmonyOS 5】鸿蒙星闪NearLink详解
【HarmonyOS 5】鸿蒙星闪NearLink详解 一、前言 鸿蒙星闪NearLink Kit 是 HarmonyOS 提供的短距离通信服务,支持星闪设备间的连接、数据交互。例如,手机可作为中心设备与外围设备(如鼠标、手写笔、智能家电、车钥匙等)通过星闪进…...

Python高级进阶:Vim与Vi使用指南
李升伟 整理 在 Python 高级进阶中,使用 Vim 或 Vi 作为代码编辑器可以显著提升开发效率,尤其是在远程服务器开发或快速脚本编辑时。以下是关于它们在 Python 开发中的高级应用详解: 1. Vim/Vi 简介 Vi:经典的 Unix 文本编辑器…...

【Python】对象生命周期全解析
Python对象生命周期全解析 在Python中,一个对象从创建到销毁会经历一系列过程,理解这些过程对于编写高效、可靠的Python代码非常重要。下面我将详细讲解Python对象的完整生命周期。 1. 对象创建阶段 (1) 内存分配 当使用类实例化时(obj MyClass())&…...
在影评情感分析中的处理流程示例)
自然语言处理(NLP)在影评情感分析中的处理流程示例
自然语言处理(NLP)在影评情感分析中的处理流程示例 以影评情感分析为例,为你详细介绍自然语言处理的处理流程。在这个例子中,我们将使用 Python 和一些常用的 NLP 库,如nltk(自然语言工具包)和…...

WF24 wifi/蓝牙模块串口与手机蓝牙通信
usb-ttl ch340接线 打开串口工具SSCOM,端口号选择ch340接的那个口,波特率改成115200 DX-SMART_2.0.5.apk下载 手机打开DX-SMART软件 点击透传-搜索BLE-连接WF24-BLE 连接成功串口会收到消息 [14:37:10.591]收←◆ BLE_CONNECT_SUCCESS发送命令ATBLUFI…...

互联网大厂Java求职面试:优惠券服务架构设计与AI增强实践-3
互联网大厂Java求职面试:优惠券服务架构设计与AI增强实践-3 场景背景 面试场景设定在一家大型互联网公司,面试官为拥有10年以上经验的技术总监,专注于高并发、高可用系统的架构设计。候选人郑薪苦是一名技术潜力十足的程序员,擅…...

C++核心编程--1 内存分区模型
C程序执行时,内存可以划分为4部分 代码区:存放函数体的二进制代码 全局区:存放全局变量、静态变量、常量 栈区:局部变量、函数参数值,编译器自动分配和释放 堆区:程序员自己分配和释放 1.1 程序运行前…...
)
02_线性模型(回归分类模型)
用于分类的线性模型 线性模型也广泛应用于分类问题,可以利用下面的公式进行预测: $ \widehat y w[0]*x[0]w[1]*x[1]…w[p]*x[p]b > 0$ 公式看起来与线性回归的公式非常相似,但没有返回特征的加权求和,而是为预测设置了阈值…...

通义千问席卷日本!开源界“卷王”阿里通义千问成为日本AI发展新基石
据日本经济新闻(NIKKEI)报道,通义千问已成为日本AI开发的新基础,其影响力正逐步扩大,深刻改变着日本AI产业的格局。 同时,日本经济新闻将通义千问Qwen2.5-Max列为全球AI模型综合评测第六名,不仅…...

流程编辑器Bpmn与LogicFlow学习
工作流技术如何与用户交互结合(如动态表单、任务分配)处理过 XML 与 JSON 的转换自定义过 bpmn.js 的样式(如修改节点颜色、形状、图标)扩展过上下文菜单(Palette)或属性面板(Properties Panel&…...

Figma 新手教程学习笔记
📺 视频地址:Figma新手教程2025|30分钟高效掌握Figma基础操作与UI设计流程_哔哩哔哩_bilibili 🧭 课程结构 Figma 简介(00:38) 熟悉工作环境(01:49) 操作界面介绍(03:…...

RabbitMQ的工作队列模式和路由模式有什么区别?
RabbitMQ 的工作队列模式(Work Queues)和路由模式(Routing)是两种不同的消息传递模式,主要区别在于消息的分发逻辑和使用场景。以下是它们的核心差异: 1. 工作队列模式(Work Queues)…...

什么是 ANR 如何避免它
一、什么是 ANR? ANR(Application Not Responding) 是 Android 系统在应用程序主线程(UI 线程)被阻塞超过一定时间后触发的错误机制。此时系统会弹出一个对话框提示用户“应用无响应”,用户可以选择等待或强…...

配置Spark环境
1.上传spark安装包到某一台机器(自己在finaShell上的机器)。 2.解压。 把第一步上传的安装包解压到/opt/module下(也可以自己决定解压到哪里)。对应的命令是:tar -zxvf 安装包 -C /opt/module 3.重命名。进入/opt/mo…...

嵌入式硬件篇---IIC
文章目录 前言1. IC协议基础1.1 物理层特性两根信号线SCLSDA支持多主多从 标准模式电平 1.2 通信流程起始条件(Start Condition)从机地址(Slave Address)应答(ACK/NACK)数据传输:停止条件&#…...

Window下Jmeter多机压测方法
1.概述 Jmeter多机压测的原理,是通过单个jmeter客户端,控制多个远程的jmeter服务器,使他们同步的对服务器进行压力测试。 以此方式收集测试数据的好处在于: 保存测试采样数据到本地机器通过单台机器管理多个jmeter执行引擎测试…...

视频图像压缩领域中 DCT 的 DC 系数和 AC 系数详解
引言 在数字图像与视频压缩领域,离散余弦变换(Discrete Cosine Transform, DCT)凭借其卓越的能量集中特性,成为JPEG、MPEG等国际标准的核心技术。DCT通过将空域信号映射到频域,分离出DC系数(直流分量&…...

K8S cgroups详解
以下是 Kubernetes 中 cgroups(Control Groups) 的详细解析,涵盖其核心原理、在 Kubernetes 中的具体应用及实践操作: 一、cgroups 基础概念 1. 是什么? cgroups 是 Linux 内核提供的 资源隔离与控制机制,…...

能源设备数据采集
在全球可持续发展目标与环境保护理念日益深入人心的时代背景下,有效管理和优化能源使用已成为企业实现绿色转型、提升竞争力的关键路径。能源设备数据采集系统,作为能源管理的核心技术支撑,通过对各类能源生产设备运行数据的全面收集、深度分…...

Go语言安装proto并且使用gRPC服务(2025最新WINDOWS系统)
1.protobuf简介 protobuf 即 Protocol Buffers,是一种轻便高效的结构化数据存储格式,与语言、平台无关,可扩展可序列化。protobuf 性能和效率大幅度优于 JSON、XML 等其他的结构化数据格式。protobuf 是以二进制方式存储的,占用空…...
