存储器上如何存储1和0
在计算机存储器中,数据最终以**二进制形式(0和1)**存储,这是由硬件特性和电子电路的物理特性决定的。以下是具体存储方式的详细解析:
一、存储的物理基础:半导体电路与电平信号
计算机存储器(如内存、硬盘等)的核心是半导体器件(如晶体管),通过电路的电信号状态表示0和1:
- 0的表示:电路处于低电平状态(如电压接近0V),代表二进制“0”。
- 1的表示:电路处于高电平状态(如电压接近5V或3.3V),代表二进制“1”。
示例:晶体管的开关状态
- 晶体管类似电子开关:
- 关闭(Off):不导通,对应低电平→存储“0”。
- 导通(On):电流通过,对应高电平→存储“1”。
二、不同存储器的存储机制
根据存储器类型(如内存、硬盘、U盘等),存储0和1的具体方式有所不同:
1. 随机存取存储器(RAM,如内存条)
- 存储单元:由电容和晶体管组成(如DRAM存储单元)。
- 电容用于存储电荷(表示0或1):
- 有电荷→高电平→“1”;
- 无电荷→低电平→“0”。
- 晶体管用于控制电容的读写操作。
- 电容用于存储电荷(表示0或1):
- 特点:
- 数据易失性:断电后电容电荷丢失,数据消失。
- 读写速度极快,用于临时存储运行中的程序和数据。
2. 固态硬盘(SSD)
- 存储单元:基于NAND闪存芯片,由浮栅晶体管组成。
- 浮栅晶体管的栅极带有电荷时,表示“1”;无电荷时表示“0”。
- 通过向浮栅注入或移除电荷,改变存储状态(如SLC、MLC、TLC等类型通过存储电荷层级区分更多数据,如TLC存储3位数据)。
- 特点:
- 非易失性:断电后电荷保留,数据不丢失。
- 速度快于机械硬盘,无机械部件。
3. 机械硬盘(HDD)
- 存储单元:基于磁性材料涂层的盘片。
- 磁头通过改变盘片表面的磁化方向记录数据:
- 正向磁化→一种磁极方向→“1”;
- 反向磁化→另一种磁极方向→“0”。
- 磁头通过改变盘片表面的磁化方向记录数据:
- 特点:
- 非易失性,但依赖机械运动,速度较慢。
4. 只读存储器(ROM,如BIOS芯片)
- 存储方式:出厂时通过掩膜工艺固定电路连接(如熔丝是否熔断)。
- 熔丝导通→“0”;熔丝熔断→“1”(或反之,取决于设计)。
- 特点:数据不可改写,用于存储固件(如主板BIOS)。
三、存储单位与数据组织
- 位(Bit):最小存储单位,一个位存储一个0或1。
- 字节(Byte):8位组成1字节(如00000001),是计算机处理数据的基本单位。
- 更大单位:KB(1024字节)、MB、GB、TB等,用于表示存储器容量。
示例:存储数字“5”
- 数字5的二进制是
00000101(1字节),在存储器中表现为:- 第1位(最高位):0(低电平)
- 第2位:0(低电平)
- ……
- 第6位:1(高电平)
- 第8位:1(高电平)
四、数据读写的核心原理
-
写入数据:
- 控制器根据数据的二进制值,向存储单元施加高/低电平(或磁场、电荷),改变其状态。
- 例:写入“1”时,对DRAM电容充电,或对SSD浮栅晶体管注入电荷。
-
读取数据:
- 通过电路检测存储单元的状态(电平、电荷、磁场方向),转换为对应的0或1。
- 例:读取DRAM时,检测电容是否有电荷,有则为“1”,无则为“0”。
五、总结:从物理到逻辑的映射
计算机存储器通过物理状态的二元化(如电平高低、电荷有无、磁极方向)实现0和1的存储,再通过电路和算法将这些二进制信号组合为字节、字符、文件等逻辑数据。这种“简单而统一”的存储方式,是现代数字计算机高效运行的基石。
二进制数据在计算机中的运算主要通过数字逻辑电路实现,核心是对二进制位(0和1)进行逻辑运算和算术运算。以下是具体原理和过程的详细解析:
一、基础逻辑运算:位运算的核心
计算机通过逻辑门电路(与门、或门、非门、异或门等)处理二进制位的基本运算,这些运算是所有复杂计算的基础。
1. 逻辑与(AND)
- 符号:
&(或电路图中的“与门”)。 - 规则:只有当两个输入位均为1时,结果为1;否则为0。
- 例:
1 & 1 = 1,1 & 0 = 0,0 & 0 = 0。
- 例:
- 电路实现:由晶体管组成的与门电路,仅当两个输入均为高电平(1)时,输出高电平(1)。
2. 逻辑或(OR)
- 符号:
|(或电路图中的“或门”)。 - 规则:只要两个输入位中有一个为1,结果为1;否则为0。
- 例:
1 | 1 = 1,1 | 0 = 1,0 | 0 = 0。
- 例:
- 电路实现:或门电路中,只要一个输入为高电平,输出即为高电平。
3. 逻辑非(NOT)
- 符号:
~(或电路图中的“非门”,带小圆圈)。 - 规则:翻转输入位,1变0,0变1。
- 例:
~1 = 0,~0 = 1。
- 例:
- 电路实现:非门(反相器)通过晶体管将输入电平反相(高变低,低变高)。
4. 逻辑异或(XOR)
- 符号:
^(或电路图中的“异或门”)。 - 规则:两个输入位不同时为1,相同时为0。
- 例:
1 ^ 1 = 0,1 ^ 0 = 1,0 ^ 0 = 0。
- 例:
- 电路实现:由与门、或门、非门组合而成,用于检测输入是否不同。
二、算术运算:加法与减法的实现
计算机的算术运算(如加减乘除)均基于二进制加法,其他运算可通过加法和逻辑运算推导实现。
1. 二进制加法
- 核心组件:全加器(Full Adder),用于计算两个二进制位及进位的和。
- 运算规则:
加数A 加数B 进位Cin 和S 新进位Cout 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1 - 关键逻辑:
- 和S:
A ^ B ^ C<sub>in</sub>(异或运算)。 - **新进位Cout
:(A & B) | (A & Cin) | (B & Cin)`(或门组合)。
- 和S:
2. 多位加法器
- 通过级联多个全加器,形成N位加法器(如32位、64位),处理多位数相加。
- 最低位全加器的进位输入Cin为0,高位全加器的进位输入来自低位的进位输出Cout。
- 示例:计算3(
011)+ 5(101)011 (3) + 101 (5) ------ = 1000(8) (进位依次传递:最低位1+1=0,进位1;中间位1+0+1=0,进位1;最高位0+1+1=0,进位1,最终结果为1000)
3. 减法运算:补码与加法的转换
- 补码表示法:将负数转换为补码形式,减法变为加法运算。
- 步骤:
- 求负数的原码(如-5的原码为
101,假设3位二进制,最高位为符号位)。 - 求反码:符号位不变,其余位取反(
101→110)。 - 求补码:反码加1(
110→111)。
- 求负数的原码(如-5的原码为
- 减法变加法:
A - B = A + (-B的补码)。
- 步骤:
- 示例:计算5(
101)- 3(011)= 5 + (-3的补码)`- -3的原码:
111(3位,符号位1)。 - -3的补码:反码
100+ 1 =101。 - 加法:
101(5) +101(-3的补码)=1010(最高位溢出,保留低3位010,即十进制2)。
- -3的原码:
三、乘法与除法:基于加法和移位
1. 乘法运算
- 原理:二进制乘法相当于“加法+移位”。
- 若乘数的某一位为1,则将被乘数左移相应位数后累加到结果中。
- 示例:计算3(
011)× 2(010)- 2的二进制最低位为0,次低位为1,故结果为
011<< 1(左移1位)=110(6)。
- 2的二进制最低位为0,次低位为1,故结果为
2. 除法运算
- 原理:二进制除法相当于“减法+移位”,通过反复比较和移位实现。
- 示例:计算6(
110)÷ 2(010):- 6右移1位(除以2)=
011(3),余数为0。
- 6右移1位(除以2)=
- 示例:计算6(
四、运算器的核心:ALU(算术逻辑单元)
- 功能:计算机的CPU中包含ALU,负责执行算术运算(加减乘除)和逻辑运算(与、或、非、异或等)。
- 组成:
- 多个全加器和逻辑门电路。
- 控制单元:根据指令选择运算类型(如加法、异或)。
- 工作流程:
- 从寄存器获取操作数(二进制数据)。
- 通过ALU执行指定运算(如加法)。
- 将结果存回寄存器或内存。
五、二进制运算的优势与挑战
优势:
- 物理实现简单:仅需区分两种状态(如电平高低),降低电路复杂度。
- 抗干扰能力强:信号只需识别高/低电平,不易受噪声影响。
- 逻辑运算统一:算术运算可转化为逻辑运算,便于电路复用。
挑战:
- 位数限制:固定位数(如32位)会导致数值溢出(结果超出表示范围)。
- 符号处理:需通过补码等方式处理正负号,增加运算复杂度。
- 浮点运算复杂:小数的二进制表示可能无限循环(如0.1的二进制为
0.000110011...),需通过浮点格式(如IEEE 754)近似表示。
总结:从电路到算法的二进制运算链
计算机通过逻辑门电路实现二进制位的基本运算,再通过全加器、移位器、补码转换等组件将简单运算组合为复杂算术操作,最终由ALU在CPU中完成高效计算。这种“以简驭繁”的设计,使得计算机能够通过最基础的0和1组合,实现从简单加减到复杂AI算法的所有运算。
加法器是计算机中实现二进制加法的核心逻辑电路,其基本原理是通过与门、或门、非门等基本逻辑门组合,实现二进制位的加法运算和进位处理。以下是不同类型加法器的实现方式:
一、半加器(Half Adder)
功能:实现两个1位二进制数(A和B)的加法,输出和(S)和进位(C),不考虑低位进位。
逻辑表达式:
- 和(S):( S = A \oplus B = A \cdot \overline{B} + \overline{A} \cdot B )(异或运算,可通过与门、或门、非门组合实现)
- 进位(C):( C = A \cdot B )(与运算)
电路图:
┌───┐ ┌───┐
A ──────┤异或├─S──┤ ├└───┘ │与门│
B ──────┤异或├────┤ ├─C└───┘ └───┘
分解实现:
- 异或门:用2个与门、1个或门和2个非门实现
- ( A \oplus B = (A \cdot \overline{B}) + (\overline{A} \cdot B) )
- 与门:直接连接A和B,输出进位C。
二、全加器(Full Adder)
功能:实现两个1位二进制数(A和B)与低位进位(Cin)的加法,输出和(S)和高位进位(Cout)。
逻辑表达式:
- 和(S):( S = A \oplus B \oplus Cin )(三次异或运算)
- 进位(Cout):( Cout = (A \cdot B) + (A \cdot Cin) + (B \cdot Cin) )(或门组合与运算结果)
电路图:
┌───┐ ┌───┐
A ────────┤半加├─S1───┐ │半加├─S
B ────────┤器 ├─C1───┼───┤器 ├└───┘ │ └───┘
Cin ────────┼─────────┘└───────────┐└───┐│或门│─Cout└───┘
分解实现:
- 第一步:用半加器计算A和B的和( S1 = A \oplus B )和进位( C1 = A \cdot B )。
- 第二步:用另一个半加器计算( S1 )和( Cin )的和( S = S1 \oplus Cin ),并得到新的进位( C2 = S1 \cdot Cin )。
- 第三步:用或门合并两次进位( Cout = C1 + C2 )。
三、多位加法器(Ripple Carry Adder)
功能:实现n位二进制数的加法,通过级联多个全加器实现,每一位的进位输出连接到下一位的进位输入。
示例:4位加法器:
全加器1 全加器2 全加器3 全加器4
┌─────┐ ┌─────┐ ┌─────┐ ┌─────┐
│A1 B1│ │A2 B2│ │A3 B3│ │A4 B4│
│ Cin─┼───> Cout│ │ Cin─┼───> Cout│
└─────┘ └─────┘ └─────┘ └─────┘S1 S2 S3 S4
特点:
- 结构简单,但进位信号需从最低位逐位传递到最高位(行波进位),运算速度较慢,位数越多延迟越长。
四、关键逻辑门的作用总结
| 逻辑门 | 功能描述 | 在加法器中的具体应用 |
|---|---|---|
| 与门(AND) | 仅当输入全为1时输出1 | 计算进位(( A \cdot B )或( A \cdot B + A \cdot Cin )) |
| 或门(OR) | 输入至少一个1时输出1 | 合并多个进位信号(如( Cout = C1 + C2 )) |
| 非门(NOT) | 翻转输入电平 | 辅助实现异或门中的取反操作(如( \overline{A} )) |
| 异或门(XOR) | 输入相异时输出1 | 计算本位和(( S = A \oplus B \oplus Cin )) |
五、扩展:减法的实现(补码加法)
计算机中减法通过补码运算转换为加法,步骤如下:
- 将减数转换为二进制补码(原码取反加1)。
- 使用加法器将被减数与减数的补码相加。
- 结果为补码形式,可自动处理符号位(负数补码的最高位为1)。
示例:计算 ( 3 - 1 )(均为4位二进制数)
- ( 3 )的原码:
0011,( 1 )的原码:0001 - ( -1 )的补码:
1111(原码1001取反1110加1) - 加法:
0011 + 1111 = 10010(舍弃最高位进位,结果为0010,即十进制2)
通过上述逻辑门的组合,计算机可实现二进制数的算术运算,而更复杂的运算(如乘法、除法)则基于加法和移位操作完成。加法器的设计优化(如超前进位加法器)可进一步提升运算速度,但核心原理仍基于基本逻辑门的组合。
相关文章:

存储器上如何存储1和0
在计算机存储器中,数据最终以**二进制形式(0和1)**存储,这是由硬件特性和电子电路的物理特性决定的。以下是具体存储方式的详细解析: 一、存储的物理基础:半导体电路与电平信号 计算机存储器(…...

2025第三届盘古初赛(计算机部分)
前言 比赛的时候时间不对,打一会干一会,导致比赛时候思路都跟不上,赛后简单复现一下,希望大家批批一下 计算机取证 1、分析贾韦码计算机检材,计算机系统Build版本为?【标准格式:19000】 183…...

【源码级开发】Qwen3接入MCP,企业级智能体开发实战!
Qwen3接入MCP智能体开发实战(上) 一、MCP技术与Qwen3原生MCP能力介绍 1.智能体开发核心技术—MCP 1.1 Function calling技术回顾 如何快速开发一款智能体应用,最关键的技术难点就在于如何让大模型高效稳定的接入一些外部工具。而在MCP技术…...

文本数据词汇级增强
import nltkfrom nltk.corpus import wordnetfrom nltk.tokenize import word_tokenizeimport random# nltk.download(wordnet)# nltk.download(punkt)def get_synonyms(word):"""获取单词的同义词列表"""synonyms []for syn in wordnet.synset…...

基于EFISH-SCB-RK3576/SAIL-RK3576的消防机器人控制器技术方案
(国产化替代J1900的应急救援智能化解决方案) 一、硬件架构设计 极端环境防护系统 防爆耐高温设计: 采用陶瓷纤维复合装甲(耐温1200℃持续1小时),通过GB 26784-2023消防设备防爆认证IP68防护等级…...

微信小程序:封装request请求、解决请求路径问题
一、创建文件 1、创建请求文件 创建工具类文件request.js,目的是用于发送请求 二、js接口封装 1、写入接口路径 创建一个变量BASE_URL专门存储api请求地址 2、获取全局的token变量 从缓存中取出token的数据 3、执行请求 (1)方法中接收传递的参数 function request(url,…...

【技术原理】ELK技术栈的历史沿革与技术演进
一、起源与早期发展(2010-2015) ELK技术栈的诞生源于互联网时代对海量日志处理的迫切需求。2010年,Elasticsearch作为基于Apache Lucene的分布式搜索引擎问世,其核心能力包括实时全文检索、倒排索引和分片存储机制,填补…...

point3d 视野朝向设置
这里写自定义目录标题 point3d 视野朝向设置三维相机朝向的直观理解 point3d 视野朝向设置 open3d.visualization.Visualizer 中的 get_view_control() 方法返回一个 ViewControl 对象,用来控制 3D 可视化窗口中的相机视角。通过这个对象可以设置视角朝向ÿ…...

windows服务器下自启动后台运行python脚本
前言 最近有个需求,在windows下根据系统的cpu核数,运行python脚本,记录下在windows注册服务,后台运行python脚本 目录 前言✅ 一、目录结构(示例)✅ 二、manager.py(启动与 CPU 数相同的子进程…...

【Elasticsearch】flattened`类型在查询嵌套数组时可能返回不准确结果的情况
好的!为了更清楚地说明flattened类型在查询嵌套数组时可能返回不准确结果的情况,我们可以通过一个具体的例子来展示。这个例子将展示如何在文档中没有完全匹配的嵌套对象时,flattened类型仍然可能返回该文档。 示例文档结构 假设你有以下文…...

Mysql、Oracle、Sql Server、达梦之间sql的差异
1:分页查询 Sql Server: <bind name"startRow" value"(page - 1) * limit 1"/> <bind name"endRow" value"page * limit"/> SELECT *FROM (SELECT ROW_NUMBER() OVER (<if test"sortZd!…...
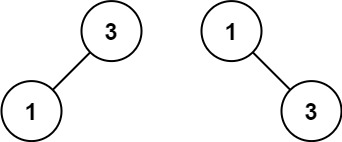
记录算法笔记(2025.5.15)将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 平衡 二叉搜索树。 示例 1: 输入:nums [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5] 解释:[0,-10,5,null,-3,null,9] 也将被视为正确…...

数学复习笔记 11
前言 向量开始。 矩阵的秩 k 阶子式。从这个概念开始复习。考虑 k 阶子式是否为零,具体是多少我们不在乎,我们只在乎 k 阶子式是否为零。把一套资料复习好就好了。 秩的计算 初等变换秩不发生改变。要么初等变换,要么行列式。用行列式需…...

Kubernetes 运维操作手册:从 etcd 快照进行精确恢复
1 5 步实现 etcd 精确恢复 将快照恢复到本地 etcd 数据目录。使用恢复的数据启动本地 etcd 实例。使用 etcdctl 查询特定键(例如,ConfigMap)。使用 auger 解码以提取干净的 YAML。使用 kubectl 申请恢复到您的实时集群。 本指南将指导您从 et…...

云轴科技ZStack官网上线Support AI,智能助手助力高效技术支持
5月16日,云轴科技ZStack在官网(www.zstack.io)正式上线ZStack Support AI智能助手。该系统是ZStack应用人工智能于技术支持服务领域的重要创新,基于自研ZStack AIOS平台智塔及LLMOPS技术打造。 ZStack Support AI定位为智能客服&…...

UE5中制作动态数字Decal
在进行城市道路编辑时,经常需要绘制人行道、交通标志、停车线等路面元素。如果能够使用具有动态修改功能的 Decal(贴花),将大大提升编辑效率和灵活性。接下来讲解如何制作。 1.首先准备一张包含所需元素的Texture,这里…...
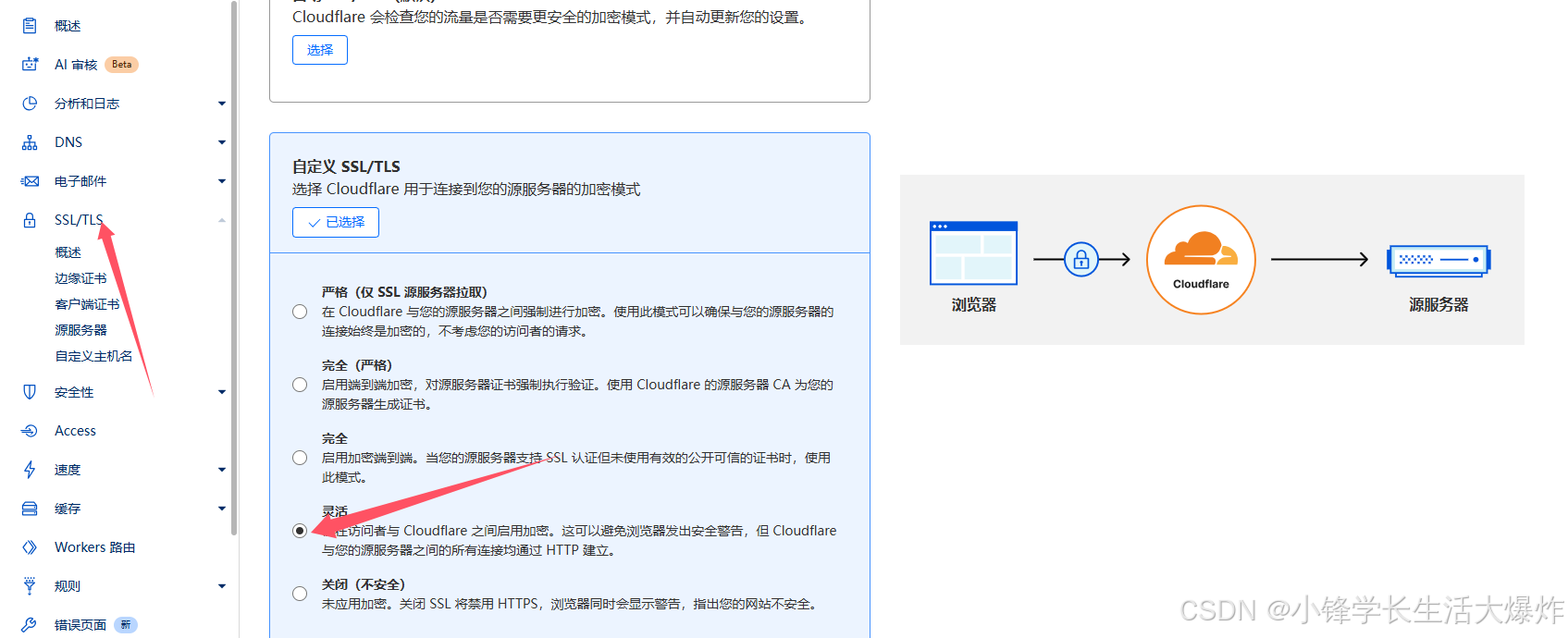
【踩坑】修复Cloudflare的Origin Rules端口重定向不生效
转载请注明出处:小锋学长生活大爆炸[xfxuezhagn.cn] 如果本文帮助到了你,欢迎[点赞、收藏、关注]哦~ 网上没人说,目前我是通过以下两种方式成功将二级域名映射到指定端口的。关于如何映射,网上教程很多,这里只说不生效…...

2025 年十大网络安全预测
随着我们逐步迈向 2026 年,网络安全领域正处于一个关键的转折点,技术创新与数字威胁以前所未有的复杂态势交织在一起。 地缘政治环境进一步加剧了这些网络安全挑战,国际犯罪组织利用先进的技术能力来追求战略目标。 人工智能在这一不断演变…...

JS手写代码篇---手写 instanceof 方法
2、手写 instanceof 方法 instancecof用于检测一个对象是否是某个构造函数的实例。它通常用于检查对象的类型,尤其是在处理继承关系时。 eg: const arr [1,2,3,4,5]console.log(arr instanceof Array); // trueconsole.log(arr instanceof Object); // true那这是…...

STM32硬件I2C驱动OLED屏幕
本文基于STM32硬件I2C驱动SSD1306 OLED屏幕,提供完整的代码实现及关键注意事项,适用于128x32或128x64分辨率屏幕。代码通过模块化设计,支持显示字符、数字、汉字及位图,并优化了显存刷新机制。 零、完整代码 完整代码: 1&#x…...

紫外相机工作原理及可应用范围
紫外相机是一种利用紫外线(UV)波段进行成像的设备,紫外线可用于机器视觉应用中,以检测使用可见光无法检测到的特征,工业上使用最常见的紫外波长是365nm和395nm。紫外相机通常用于高分辨率视频显微镜、电晕检测、半导体…...

【虚幻引擎】UE5独立游戏开发全流程(商业级架构)
本套课程我将会讲解一下知识 1.虚幻引擎的常用功能节点、模块包含但不限于动画模块、UI模块、AI模块、碰撞模块、伤害模块、背包模块、准心模块、武器模块、可拾取物品模块、死亡等模块。 2.整个游戏的设计思路(游戏架构),本套教程讲解了如…...

嵌入式单片机中STM32F1演示寄存器控制方法
该文以STM32F103C8T6为示例,演示如何使用操作寄存器的方法点亮(关闭LED灯),并讲解了如何调试,以及使用宏定义。 第一:操作寄存器点亮LED灯。 (1)首先我们的目的是操作板子上的LED2灯,对其实现点亮和关闭操作。打开STM32F103C8T6的原理图,找到LED2的位置。 可以看到…...

spark-cache模式
一、RDD持久化 1.什么时候该使用持久化(缓存) 2. RDD cache & persist 缓存 3. RDD CheckPoint 检查点 4. cache & persist & checkpoint 的特点和区别 特点 区别 二、cache & persist 的持久化级别及策略选择 Spark的几种持久化…...

架构思维:通用架构模式_系统监控的设计
文章目录 引言什么是监控三大常见监控类型1. 次数监控2. 性能监控3. 可用率监控 落地监控1. 服务入口2. 服务内部3. 服务依赖 监控时间间隔的取舍小结 引言 架构思维:通用架构模式_从设计到代码构建稳如磐石的系统 架构思维:通用架构模式_稳如老狗的SDK…...

Laravel 参数验证工具
Laravel 提供了内置的参数验证工具,可以让你定义参数需满足的规则,程序自动进行验证。如果验证成功,程序继续运行;如果失败,则自动返回响应并显示失败原因。 具体实现方式如下: 1. 创建自定义请求类 你可…...

InfluxDB 2.7 连续查询实战指南:Task 替代方案详解
InfluxDB 2.7 引入了 Task 功能,作为连续查询(CQ)的现代替代方案。本文详细介绍了如何使用 Task 实现传统 CQ 的功能,包括语法解析、示例代码、参数对比以及典型应用场景。通过实际案例和最佳实践,帮助开发者高效迁移并…...
【SpringBoot】从零开始全面解析SpringMVC (二)
本篇博客给大家带来的是SpringBoot的知识点, 本篇是SpringBoot入门, 介绍SpringMVC相关知识. 🐎文章专栏: JavaEE进阶 🚀若有问题 评论区见 👉gitee链接: 薯条不要番茄酱 ❤ 欢迎大家点赞 评论 收藏 分享 如果你不知道分享给谁,那就分享给薯条…...

蒟蒻编程日志
ORZ (用于记录你这个“人”是不是真的,也就是说CSDN的流量是否属合适) 2025/4/14 21:25 开坑 前言 2024/10/26:CSP-J 260pts,CSP-S 45pts。 2025/3/1:%你赛 180pts rk34 寄!这就是不认真的…...

git克隆github项目到本地的三种方式
本文旨在使用git工具将别人发布在github上的项目保存到本地 1.安装git,创建github账户,并使用ssh关联自己的github账号和git,具体教程可以参照下面两篇文章: Github入门教程,适合新手学习(非常详细&#…...
