经典算法 求C(N, K) % mod,保证mod是质数
求C(N, K) % mod,保证mod是质数
问题描述
给你三个整数N,K,mod保证mod是一个质数,求组合数C(N, K) % mod。
输入描述
输入有多组,输入第一行为两个整数T,mod。接下来2 - T + 1行,每行输入N, K。
输出描述
每一组输入,输出C(N, K) % mod。
输入示例
9 1000003
6 4
7 5
3 2
10 5
100 50
1000 500
10000 5000
100000 50000
1000000 500000
输出示例
15
21
3
252
440004
175726
737315
781911
375001
c++代码(乘法逆元)
这种方法大致可以处理N,K<= 1000000,mod <= 1000000009。
保证mod为质数,用费马小定理求逆元。
#include<bits/stdc++.h>using namespace std;typedef __int128_t ll;//防止数据溢出long long T, N, K, mod;//保证mod是质数
vector<ll> jiecen;ll fastPow(ll a, ll b, ll mod) {//返回a^b % modif (b == 0) return 1 % mod;if (b == 1) return a % mod;ll k = fastPow(a, b / 2, mod);if (b % 2 == 0) return (k * k) % mod;else return (((k * k) % mod) * a) % mod;
}ll mod_inverse(ll A, ll mod) { return fastPow(A, mod - 2, mod); }//求A % mod 的逆元ll cnk(ll N, ll K, ll mod) { return (jiecen[N] * mod_inverse((jiecen[K] * jiecen[N - K]) % mod, mod)) % mod; }//返回组合数C(N, K) % modint main() {cin >> T >> mod;jiecen = vector<ll>(1000001, 1);//预处理阶乘for (int i = 1; i <= 1000000; i++) jiecen[i] = (jiecen[i - 1] * i) % mod;while(T--) {cin >> N >> K;cout << (long long)cnk(N, K, mod) << endl;}return 0;
}//by wqs
c++代码(卢卡斯定理)
大致可以处理N,K <= 1 * 10^18, mod <= 1000000。
卢卡斯递归过程中可能会出现N < K,这个时候cnk函数要返回0
#include<bits/stdc++.h>using namespace std;typedef __int128_t ll;vector<ll> jiecen;
long long T, N, K, mod;ll fastPow(ll a, ll b, ll mod) {//返回a^b % modif (b == 0) return 1 % mod;if (b == 1) return a % mod;ll k = fastPow(a, b / 2, mod);if (b % 2 == 0) return (k * k) % mod;else return (((k * k) % mod) * a) % mod;
}ll mod_inverse(ll A, ll mod) { return fastPow(A, mod - 2, mod); }//求A % mod 的逆元ll cnk(ll N, ll K, ll mod) { return N >= K ? (jiecen[N] * mod_inverse((jiecen[K] * jiecen[N - K]) % mod, mod)) % mod : 0; }//返回组合数C(N, K) % modll Lucas(ll N, ll K, ll mod) { return K == 0 ? 1 : (cnk(N % mod, K % mod, mod) * Lucas(N / mod, K / mod, mod)) % mod; }int main() {cin >> T >> mod;jiecen = vector<ll>(mod, 1);for (int i = 1; i <= mod - 1; i++) jiecen[i] = (__int128_t(jiecen[i - 1]) * i) % mod;while(T--) {cin >> N >> K;cout << (long long)Lucas(N, K, mod) << endl;}return 0;
}//by wqs
相关文章:
 % mod,保证mod是质数)
经典算法 求C(N, K) % mod,保证mod是质数
求C(N, K) % mod,保证mod是质数 问题描述 给你三个整数N,K,mod保证mod是一个质数,求组合数C(N, K) % mod。 输入描述 输入有多组,输入第一行为两个整数T,mod。接下来2 - T 1行,每行输入N, K。 输出描…...

【LeetCode 热题 100】二叉树的最大深度 / 翻转二叉树 / 二叉树的直径 / 验证二叉搜索树
⭐️个人主页:小羊 ⭐️所属专栏:LeetCode 热题 100 很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~ 目录 二叉树的中序遍历二叉树的最大深度翻转二叉树对称二叉树二叉树的直径二叉树的层序遍历将有序数组转换为二叉搜索树验…...

关于软件测试开发的一些有趣的知识
文章目录 一、什么是测试?二、为什么要软件测试软件测试三、测试的岗位有哪些四 、软件测试和开发的区别五、走测试岗位为什么还要学开发。4、优秀的测试人员具备的素质我为什么走测试岗位 一、什么是测试? 其实这个问题说简单也不简单,说难…...

uni-app 开发HarmonyOS的鸿蒙影视项目分享:从实战案例到开源后台
最近,HBuilderX 新版本发布,带来了令人兴奋的消息——uni-app 现在支持 Harmony Next 平台的 App 开发。这对于开发者来说无疑是一个巨大的福音,意味着使用熟悉的 Vue 3 语法和开发框架,就可以为鸿蒙生态贡献自己的力量。 前言 作…...

售前工作.工作流程和工具
第一部分 售前解决方案及技术建议书的制作 售前解决方案编写的标准操作步骤SOP: 售前解决方案写作方法_哔哩哔哩_bilibili 第二部分 投标过程关键活动--商务标技术方案 1. 按项目管理--售前销售项目立项 销售活动和销售线索的跟踪流程和工具 1)拿到标书ÿ…...
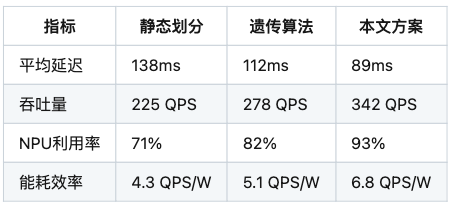
GPU与NPU异构计算任务划分算法研究:基于强化学习的Transformer负载均衡实践
点击 “AladdinEdu,同学们用得起的【H卡】算力平台”,H卡级别算力,按量计费,灵活弹性,顶级配置,学生专属优惠。 引言 在边缘计算与AI推理场景中,GPU-NPU异构计算架构已成为突破算力瓶颈的关键技…...

学习ai课程大纲
以下是一个通用的 AI 课程大纲,涵盖从基础到进阶的核心内容,适用于大学课程或自学规划。你可以根据自身需求(如入门、进阶、专项方向)调整内容和深度。 人工智能(AI)课程大纲 第一部分:基础理论…...

基于CentOS7制作OpenSSL 1.1的RPM包
背景:CentOS7 已经不再维护了,有时候需要升级某些组件,网上却没有相关的资源了。尤其是制作OpenSSH 9.6 的RPM包,就会要求OpenSSL为1.1的版本。基于此,还是自己制作吧,以下是踩坑过程。 1、官网提供的源码包…...

数据分析_Python
1 分析内容 1.1 数据的整体概述 提供数据集的基本信息,包括数据量、时间跨度、地理范围和主要字段. import pandas as pd# 创建示例数据 data {姓名: [张三, 李四, 王五, 赵六, 钱七, 孙八, 周九, 吴十],年龄: [25, 30, 35, 40, 45, 50, 55, 60],性别: [男, 男, 女, 女, 男,…...

TCP/UDP协议原理和区别 笔记
从简单到难吧 区别就是TCP一般用于安全稳定的需求,UDP一般用于不那么需要完全数据的需求,比如说直播,视频等。 再然后就是TPC性能慢于UDP。 再然后我们看TCP的原理(三次握手,数据传输,四次挥手࿰…...

深入浅出:C++数据处理类与计算机网络的巧妙类比
深入浅出:C数据处理类与计算机网络的巧妙类比 引言 在计算机编程中,我们常常会遇到一些看似简单的代码结构,却能巧妙地映射到复杂的计算机网络概念中。本文将通过一个简单的C数据处理类,探讨其与计算机网络中硬件设备和协议的类…...

【滑动窗口】LeetCode 209题解 | 长度最小的子数组
长度最小的子数组 前言:滑动窗口一、题目链接二、题目三、算法原理解法一:暴力枚举解法二:利用单调性,用滑动窗口解决问题那么怎么用滑动窗口解决问题?分析滑动窗口的时间复杂度 四、编写代码 前言:滑动窗口…...

在RK3588上使用NCNN和Vulkan加速ResNet50推理全流程
在RK3588上使用NCNN和Vulkan加速ResNet50推理全流程 前言:为什么需要关注移动端AI推理一、环境准备与框架编译1.1 获取NCNN源码1.2 安装必要依赖1.3 编译NCNN二、模型导出与转换2.1 生成ONNX模型2.2 转换NCNN格式三、模型量化加速3.1 生成校准数据3.2 执行量化操作四、性能测试…...

【ant design】ant-design-vue 4.0实现主题色切换
官网:Ant Design Vue — An enterprise-class UI components based on Ant Design and Vue.js 我图方便,直接在 app.vue 中加入的 <div class"app-content" v-bind:class"appOption.appContentClass"><a-config-provider…...

Android 图片自动拉伸不变形,点九
要让 UI 设计师 制作 Android 用的点九图(.9.png),可以按照以下流程和要求进行: 🧩 一、什么是点九图? 点九图(NinePatch)是一种特殊的 PNG 图像,用于在 Android 中根据…...

电子电路:什么是色环电阻器,怎么识别和计算阻值?
识别和计算色环电阻的阻值需要掌握颜色编码规则和基本步骤。以下是具体方法及窍门: 一、色环电阻的基本规则 色环数量: 4环电阻:前2环为有效数字,第3环为倍乘(10ⁿ),第4环为误差。5环电阻:前3环为有效数字,第4环为倍乘,第5环为误差。6环电阻(较少见):前3环为有效数…...

LeetCode Hot100刷题——轮转数组
56. 轮转数组 给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。 示例 1: 输入: nums [1,2,3,4,5,6,7], k 3 输出: [5,6,7,1,2,3,4] 解释: 向右轮转 1 步: [7,1,2,3,4,5,6] 向右轮转 2 步: [6,7,1,2,3,4,5] 向右轮转 3 步: …...

Python绘制南丁格尔玫瑰图:从入门到实战
Python绘制南丁格尔玫瑰图:从入门到实战 引言 南丁格尔玫瑰图(Nightingale Rose Chart),也被称为极区图(Polar Area Chart),是一种独特的数据可视化方式。这种图表由弗洛伦斯南丁格尔ÿ…...

概率与期望总结
一、概率 概念:无需多言;几个公式( Ω \Omega Ω 表示整个样本空间): 以下公式均有 A , B ⊆ Ω , 且 P ( A ) , P ( B ) > 0. P ( A ∪ B ) P ( A ) P ( B ) − P ( A ∩ B ) , P ( A ∣ B ) P ( A B ) P ( B…...

炼丹学习笔记3---ubuntu2004部署运行openpcdet记录
前言 环境 cuda 11.3 python 3.8 ubuntu2004 一、cuda环境检测 ylhy:~/code_ws/OpenPCDet/tools$ nvcc -V nvcc: NVIDIA (R) Cuda compiler driver Copyright (c) 2005-2021 NVIDIA Corporation Built on Sun_Mar_21_19:15:46_PDT_2021 Cuda compilation tools, release 11.3…...

深入解析BGP路由反射器与联邦:突破IBGP全连接限制的两种方案
一、引言:大型BGP网络的挑战 在大型BGP网络架构中,传统的IBGP全连接架构会带来严重的扩展性问题。当网络中存在N台路由器时,需要维护N*(N-1)/2个IBGP连接,这对设备资源和运维管理都是巨大挑战。本文将深入解析两种主流解决方案&a…...

QT设置MySQL驱动
QSqlDatabase: QMYSQL driver not loaded QSqlDatabase: available drivers: QSQLITE QMYSQL QMYSQL3 QODBC QODBC3 QPSQL QPSQL7 第一步:下载MySQL https://dev.mysql.com/downloads/mysql/ 解压缩下载的安装包,其目录结构如下所示: 第二…...

String的一些固定程序函数
append reverse length toString...

3.2/Q2,Charls最新文章解读
文章题目:Transition of nighttime sleep duration and sleep quality with incident cardiovascular disease among middle-aged and older adults: results from a national cohort study DOI:10.1186/s13690-025-01577-5 中文标题:中老年人…...

大麦(Hordeum vulgare)中 BAHD 超家族酰基转移酶-文献精读129
Systematic identification and expression profiles of the BAHD superfamily acyltransferases in barley (Hordeum vulgare) 系统鉴定与大麦(Hordeum vulgare)中 BAHD 超家族酰基转移酶的表达谱分析 摘要 BAHD 超家族酰基转移酶在植物中催化和调控次…...

docker迅雷自定义端口号、登录用户名密码
在NAS上部署迅雷,确实会带来很大的方便。但是目前很多教程都是讲怎么部署docker迅雷,鲜有将自定义配置的方法。这里讲一下怎么部署,并重点讲一下支持的自定义参数。 一、部署docker 在其他教程中,都是介绍的如下命令,…...

中国30米年度土地覆盖数据集及其动态变化(1985-2022年)
中文名称 中国30米年度土地覆盖数据集及其动态变化(1985-2022年) 英文名称:The 30 m annual land cover datasets and its dynamics in China from 1985 to 2022 CSTR:11738.11.NCDC.ZENODO.DB3943.2023 DOI 10.5281/zenodo.8176941 数据共享方式:…...

3D个人简历网站 5.天空、鸟、飞机
1.显示天空 models下新建文件Sky.jsx Sky.jsx // 从 React 库中导入 useRef 钩子,用于创建可变的 ref 对象 import { useRef } from "react"; // 从 react-three/drei 库中导入 useGLTF 钩子,用于加载 GLTF 格式的 3D 模型 import { useGLT…...

STM32IIC实战-OLED模板
STM32IIC实战-OLED模板 一,SSD1306 控制芯片1, 主要特性2,I2C 通信协议3, 显示原理4, 控制流程5, 开发思路 二,HAL I2C API 解析I2C 相关 API1,2,3,4…...

Sparse4D运行笔记
Sparse4D有三个版本,其中V1和V2版本的官方文档中环境依赖写得比较模糊且依赖库有版本冲突。 1. Sparse4D V1 创建环境 conda create sparse4dv1 python3.8 激活环境 conda activate sparse4dv1 安装torch, torchvision, torchaudio pip install torch1.13.0c…...
