6.1.1图的基本概念
基本概念
图:
顶点集+边集
顶点集:所有顶点的集合,不能为空(因为图是顶点集和边集组成,其中一个顶点集不能为空,则图肯定不为空)
边集:所有边的集合,边是由顶点集中的2个顶点构成,如果边集里的边不是由顶点集里的2个顶点构成,那就构不成图,可以为空




无向图:
(只有度、边、连通、连通图、极大连通子图(连通分量)、生成树、带权路径长度的概念)
各个边没有方向,A和B有一条线,则A可以到B,B可以导A。边用圆括号(),(A,B)=(B,A)
度:
依附于该顶点的边的条数,也就是这个顶点有多少条线。记为TD(V)。TD(C)=2。一条边为2个顶点提供一个度,即无向图的度数之和是边数的2倍
有向图:
(只有入度、出度、弧头、弧尾,强连通、强连通图、强连通分量概念):
各个边有方向,各个边又称为弧,用尖括号<>表示边,<A,B>≠<B,A>,A指向B,B没有指向A,则B就不能到A。有箭头指向的顶点称为弧头,没有箭头指向的顶点称为弧尾,如<v,w>是从v到w的距离,v指向w,w是是弧头,v是弧尾
顶点的入度:
以该顶点为基准,往该顶点指的箭头有几个。有多少边指向该顶点。ID(A)=1
顶点的出度:
以该顶点为基准,往外指的箭头有几个。该顶点指向多少边。OD(A)=4
简单图:没有顶点到自身的边+没有重复边
多重图:加了顶点到自身的边
路径(2个顶点之间):
从1个顶点到另外一个顶点经过了哪些顶点序列(顶点可以重复,没有重复的顶点序列就是简单路径)。
距离(2个顶点之间):
路径的长度。估摸是路径中的顶点序列个数
无向图A到D的路径:ABD顶点序列(简单路径)或ABED(简单路径)序列或ABECD(简单路径)序列或ABEBD(出现重复顶点B,不是简单路径,但还是路径)即顶点序列
无向图连通(2个顶点之间):
从一个顶点到另外一个顶点之间有没有路径存在,有路径就是连通,没路径就是不连通。F顶点没边,即和其他顶点没有连接,没有路径,不连通,没有路径的距离都是∞,距离都是最短序列(没边的顶点都没有路径,没有路径的距离都是∞)
有向图强连通(2个顶点之间):
如果从A到E有路径,从E到A有路径,则称为两个顶点强连通。如果有向图A到E有路径,E到A没有路径,因为没有从E指出的箭头,
连通图:
针对无向图来说,任意2个顶点都是连通的,即都有路径,称为连通图,否则称为非连通图。
强连通图:
针对有向图来说,任意2个顶点都是强连通的,就是强连通图



子图:
从一个图的顶点集合拿出一些顶点,再从图的边集里拿出一些边,拿出的边集和顶点集构成的图(一定要构成图,有的还构不成图,如下图就够不成图)就是原图的子图
生成子图:
有2个图,图A和图B,图A和图B的顶点集完全相同,但是图B的边集比图A的边集少(即少几条边)那图B就是图A的生成子图


连通分量(极大,无向图):
极大连通子图(无向图的子图中的任意2个顶点之间都是连通的,即有路径,并且尽可能都多的顶点和边)称为连通分量
连通分量如下:无向图中G的三个子图中都是连通图(任意2个顶点之间都有路径,子图G只有一个顶点没边,所以认为也是连通的吧,各个子图带多个顶点啥的就不是连通图了,比如把J这个顶点放到GHI这个子图里,GHI子图就不连通了),且尽可能多的包含了无向图G中的顶点和边(那意思是无向图G原来不是连通图吧,因为J这个顶点和任意顶点都不连通且G、I、H和带A的子图也不连通)
强连通分量(有向图):
有向图中的ABCDE顶点是强连通的(因为各个顶点之间可以逆推),但是加上F顶点不是(因为ABCDE顶点都可以推到F顶点,即连通,但是F顶点没有到ABCDE的箭头指向,即没有路径不能逆推,故不是强联通的),所以要把F顶点抽离出来,G顶点同,故构成如下三个强联通子图即强连通分量(跟无向图类似,还是让每个子图尽量有多的可强连通的顶点和边)


生成树(极小):
针对无向图来说,首先生成树包含图中的所有顶点还要保持连通,但是还要在连通的请情况下保证边少,即在保证连通的情况下,顶点数-1为最少的边数,因为少一条边的树有各种形式,则一个图的生成树可能有多条。对于生成树而言,少一条边就会变成非连通图,多一条边就会形成一个回路。
一般生成树用于各个没有打通的村修路,各个村就相当于各个顶点,要让各个村打通,不一定要把各个村之间都修上路,因为花费太大,所以可以使用生成树的概念,在保证各个村连通的前提下,有最少的边,边修少了意味着修路的花费变少,且因为一个图的生成树样式不只一种,则可以根据现实中修每条路的实际成本有多少,来确定到底怎样修路

生成森林:
顺序是图是非连通图,然后形成一个个连通分量(各个连通分量都是连通的且是图的极大连通子图,即在保证连通的前提下,每个连通分量拥有尽可能多的图的顶点和边),然后连通分量再形成生成树(生成树都是连通的,且生成树拥有连通分量的全部顶点和在保证连通的前提下尽可能少的边),然后就形成了生成森林(估摸是所有的连通分量的生成树合在一起叫生成森林吧)


带权路径长度:
给路径标上值,从北京到上海的带权路径长度=经过的路径上标的值之和
带权图:
给路径上标值的图




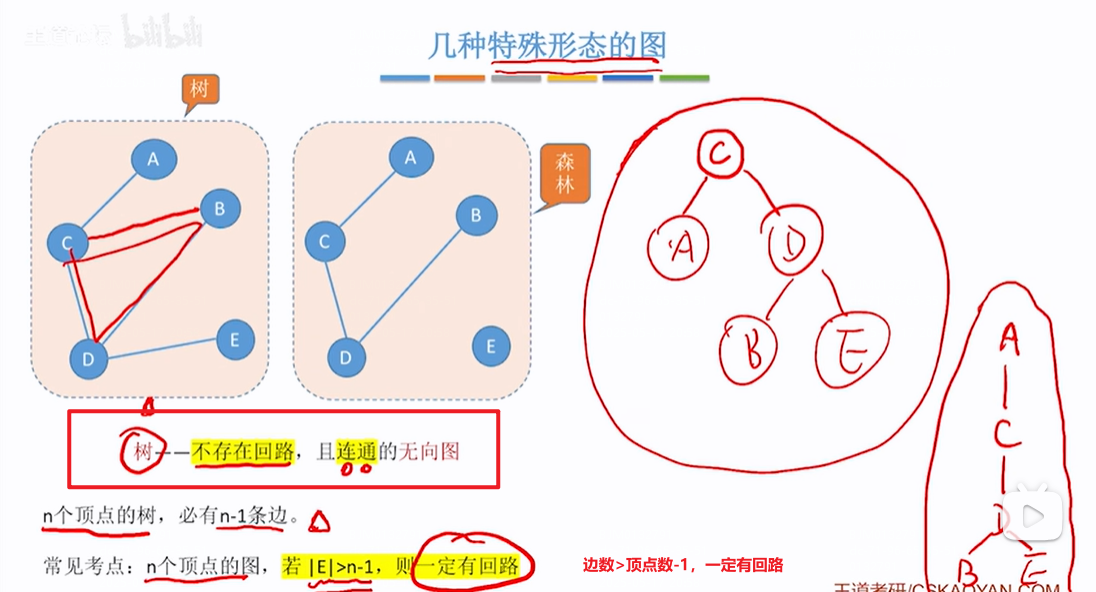
有向树并不是强连通图,不是不都是是不是强连通图


做个记录。。。。。。
相关文章:

6.1.1图的基本概念
基本概念 图: 顶点集边集 顶点集:所有顶点的集合,不能为空(因为图是顶点集和边集组成,其中一个顶点集不能为空,则图肯定不为空) 边集:所有边的集合,边是由顶点集中的2…...

Linux面试题集合(6)
创建多级目录或者同级目录 mkdir -p 文件名/文件名/文件名 mkdir -p 文件名 文件名 文件名 Linux创建一个文件 touch 文件名 DOS命令创建文件 echo 内容>文件名(创建一个有内容的文件) echo >文件名(创建一个没有内容的文件)…...

时间筛掉了不够坚定的东西
2025年5月17日,16~25℃,还好 待办: 《高等数学1》重修考试 《高等数学2》备课 《物理[2]》备课 《高等数学2》取消考试资格学生名单 《物理[2]》取消考试资格名单 职称申报材料 2024年税务申报 5月24日、25日监考报名 遇见:敲了一…...

Python集合运算:从基础到进阶全解析
Python基础:集合运算进阶 文章目录 Python基础:集合运算进阶一、知识点详解1.1 集合运算(运算符 vs 方法)1.2 集合运算符优先级1.3 集合关系判断方法1.4 方法对比 二、说明示例2.1 权限管理系统2.2 数据去重与差异分析2.3 数学运算…...
openjdk17 c++源码垃圾回收安全点信号函数处理线程阻塞)
jvm安全点(二)openjdk17 c++源码垃圾回收安全点信号函数处理线程阻塞
1. 信号处理与桩代码(Stub) 当线程访问安全点轮询页(Polling Page)时: 触发 SIGSEGV 信号:访问只读的轮询页会引发 SIGSEGV 异常。信号处理函数:pd_hotspot_signal_handl…...

YOLOv7训练时4个类别只出2个类别
正常是4个类别: 但是YOLOv7训练完后预测总是只有两个类别: 而且都是LFM和SFM 我一开始检查了下特征图大小,如果输入是640*640的话,三个尺度特征图是80*80,40*40,20*20;如果输入是416*416的话,三个尺度特征…...

【论文阅读】针对BEV感知的攻击
Understanding the Robustness of 3D Object Detection with Bird’s-Eye-View Representations in Autonomous Driving 这篇文章是发表在CVPR上的一篇文章,针对基于BEV的目标检测算法进行了两类可靠性分析,即恶劣自然条件以及敌对攻击。同时也提出了一…...

18.中介者模式:思考与解读
原文地址:中介者模式:思考与解读 更多内容请关注:深入思考与解读设计模式 引言 在软件开发中,尤其是处理多个对象交互时,你是否遇到过一个问题:当多个对象需要互相通信时,系统变得复杂,难以管…...

flutter 配置 安卓、Ios启动图
android 配置启动图 launch_background.xml <?xml version"1.0" encoding"utf-8"?> <!-- Modify this file to customize your launch splash screen --> <layer-list xmlns:android"http://schemas.android.com/apk/res/android&…...

基于朴素贝叶斯与 LSTM 的假新闻检测模型对比分析
一、引言 在信息爆炸的时代,假新闻的传播对社会产生了诸多负面影响。如何快速、准确地识别假新闻成为了重要的研究课题。本文将对比传统机器学习算法(朴素贝叶斯)与深度学习模型(LSTM)在假新闻检测任务中的性能表现&am…...

【LeetCode 热题 100】搜索插入位置 / 搜索旋转排序数组 / 寻找旋转排序数组中的最小值
⭐️个人主页:小羊 ⭐️所属专栏:LeetCode 热题 100 很荣幸您能阅读我的文章,诚请评论指点,欢迎欢迎 ~ 目录 搜索插入位置搜索二维矩阵在排序数组中查找元素的第一个和最后一个位置搜索旋转排序数组寻找旋转排序数组中的最小值…...
副业小程序YUERGS,从开发到变现
文章目录 我为什么写这个小程序网站转小程序有什么坑有什么推广渠道个人开发者如何变现简单介绍YUERGS小程序给独立开发者一点小建议 我为什么写这个小程序 关注我的粉丝应该知道,我在硕士阶段就已经掌握了小程序开发技能,并写了一个名为“约球online”…...
)
计算机视觉与深度学习 | Python实现EMD-VMD-LSTM时间序列预测(完整源码和数据)
EMD-VMD-LSTM 一、完整代码实现二、代码结构解析三、关键参数说明四、性能优化建议五、工业部署方案以下是用Python实现EMD-VMD-LSTM时间序列预测的完整代码,结合经验模态分解(EMD)、变分模态分解(VMD)与LSTM深度学习模型,适用于复杂非平稳信号的预测任务。代码包含数据生…...

基于LLM合成高质量情感数据,提升情感分类能力!!
摘要:大多数用于情感分析的数据集缺乏意见表达的上下文,而上下文对于理解情绪往往至关重要,并且这些数据集主要局限于几种情绪类别。像 GPT-4 这样的基础大型语言模型(Foundation Large Language Models,LLMsÿ…...

网络检测工具InternetTest v8.9.1.2504 单文件版,支持一键查询IP/DNS、WIFI密码信息
—————【下 载 地 址】——————— 【本章下载一】:https://drive.uc.cn/s/295e068b79314 【本章下载二】:https://pan.xunlei.com/s/VOQDXguH0DYPxrql5y2zlkhTA1?pwdg2nx# 【百款黑科技】:https://ucnygalh6wle.feishu.cn/wiki/…...

SpringBoot中使用Flux实现流式返回的技术总结
背景 近期在使用deepseek/openai等网页和APP时,发现大模型在思考和回复时,内容是一点点的显示出来的,于是好奇他们的实现方式。经调研和使用开发者工具抓取请求,每次聊天会向后台发送一个http请求,而这个接口跟普通接…...

【网络编程】十、详解 UDP 协议
文章目录 Ⅰ. 传输层概述1、进程之间的通信2、再谈端口号端口号的引出五元组标识一个通信端口号范围划分常见的知名端口号查看知名端口号协议号 VS 端口号 3、两个问题一个端口号是否可以被多个进程绑定?一个进程是否可以绑定多个端口号? 4、部分常见指令…...

从零开始理解Jetty:轻量级Java服务器的入门指南
目录 一、Jetty是什么?先看一个生活比喻 二、5分钟快速入门:搭建你的第一个Jetty服务 步骤1:Maven依赖配置 步骤2:编写简易Servlet(厨房厨师) 步骤3:组装服务器(餐厅开业准备&am…...

python05——循环结构
1、while循环 n0 #初始条件 while n<5: #判断print(hello python) #要重复执行的代码print(n) #注意同级代码缩进相同n1 #计数器结果: hello python 0 hello python 1 hello python 2 hello python 3 hello python 4 hello python 5 #求阶乘和 sum0 n1 whil…...

windows触摸板快捷指南
以下是结构化整理后的触控手势说明,采用清晰的层级划分和标准化表述: **触控手势操作规范****1. 单指操作****2. 双指操作****3. 三指操作****4. 四指操作** **优化说明:** 触控手势操作规范 1. 单指操作 手势功能描述等效操作单击滑动选择…...

STM32 ADC 模数转换器详解:原理、配置与应用
STM32 ADC 模数转换器详解:原理、配置与应用 在嵌入式系统中,模数转换(ADC)是实现传感器信号采集、信号处理等任务的关键环节。STM32 微控制器作为一款功能强大的 32 位微控制器,其内置的 ADC 模块为开发者提供了高效…...

[目标检测] YOLO系列算法讲解
前言 目标检测就是做到给模型输入一张图片或者视频,模型可以迅速判断出视频和图片里面感兴趣的目标所有的位置和它 的类别,而当前最热门的目标检测的模型也就是YOLO系列了。 YOLO系列的模型的提出,是为了解决当时目标检测的模型帧率太低而提…...

React 中,闭包陷阱
文章目录 前言1. 经典闭包陷阱示例过期状态问题 2. 解决方案2.1 正确声明依赖数组2.2 使用 useRef 捕获最新值**2.3 使用函数式更新(针对状态更新)****2.4 使用 useCallback 冻结闭包** **3. 异步操作中的闭包陷阱****事件监听示例** **4. 自定义 Hooks …...

.NET NativeAOT 指南
目录 1. 引言 2. 什么是 .NET NativeAOT? 2.1 NativeAOT 的定义 2.2 NativeAOT 与传统 JIT 的对比 2.3 NativeAOT 的适用场景 3. NativeAOT 的核心优势 3.1 性能提升 3.2 简化部署 3.3 更小的应用体积 3.4 知识产权保护 4. NativeAOT 的基本用法 4.1 环境…...

uniapp-商城-57-后台 新增商品(弹窗属性数据添加父级)
后台增加商品,需要添加相关的数据信息,这里还要添加属性,前面已经对相关的界面布局继续了编写。这里还要对页面添加的数据,置入到云数据库,继续永久保存,便于后期的使用。这里主要是讲属性数据 父级信息的添…...

摩方 12 代 N200 迷你主机(Ubuntu 系统)WiFi 抓包环境配置教程
摩方12代N200迷你主机标配 Intel AX201无线网卡,支持 WiFi 6 协议(802.11ax)及蓝牙5.2。此网卡兼容主流抓包工具,但需注意: 驱动兼容性:Ubuntu 20.04及以上内核版本(5.4)默认支持AX2…...

matlab多智能体网络一致性研究
一个基于连续时间多智能体系统(Multi-Agent Systems, MAS)的一阶一致性协议的MATLAB仿真代码,包含网络拓扑建模、一致性协议设计和收敛性分析。代码支持固定拓扑和时变拓扑,适用于学术研究。 1. 基础模型与代码框架 (1) 网络拓扑…...

Unity(URP渲染管线)的后处理、动画制作、虚拟相机(Virtual Camera)
一、URP渲染管线 渲染管线是一系列渲染操作的集合,Unity提供了内置渲染管线(Built-In)和可编程渲染管线(SRP)两类渲染管线。内置渲染管线是Unity的默认渲染管线,其自定义选项有限。而可编程渲染管线可以通…...

C语言:在 Win 10 上,gcc 如何编译 gtk 应用程序
在 Windows 10 上使用 g(或 gcc)编译基于 GTK 的 C 语言程序是完全可行的,且相比 Tcc 更为推荐,因为 g(GNU 编译器套件)对 GTK 的支持更加完善,配置也更简单。以下是详细步骤和注意事项…...
)
阿里云CMH镜像迁移与SMC整机迁移对比及功能详解(同地域跨主体账号场景)
文章目录 一、核心功能对比二、CMH镜像迁移操作流程1.资源调研2.镜像共享3.迁移验证4.限制: 三、SMC整机迁移操作流程1.迁移源导入2.任务配置3.增量同步4.应用验证…...
