卷积神经网络进阶:转置卷积与棋盘效应详解
【内容摘要】
本文深入解析卷积神经网络中的转置卷积(反卷积)技术,重点阐述标准卷积与转置卷积的计算过程、转置卷积的上采样作用,以及其常见问题——棋盘效应的产生原因与解决方法,为图像分割、超分辨率等任务提供理论支持。
关键词: 转置卷积 反卷积 棋盘效应 标准卷积 上采样 卷积神经网络
在卷积神经网络(CNN)中,转置卷积(Transposed Convolution,又称反卷积Deconvolution)是实现特征图上采样的关键技术,广泛应用于语义分割、超分辨率等需要恢复空间分辨率的任务中。本文将从标准卷积的计算原理出发,详细解析转置卷积的操作过程,并重点讨论其常见问题——棋盘效应的产生机制与解决方法。
一、标准卷积的计算过程
要理解转置卷积,首先需要明确标准卷积的运算方式。标准卷积是通过卷积核对输入特征图进行滑窗点乘求和的过程,其核心步骤包括卷积核旋转(通常为180°)、中心对齐与局部区域计算。
以图1所示的标准卷积输出计算为例,输入为一个3×3的像素矩阵,卷积核为3×3的矩阵(值为[-1,-2,-1;0,0, 0;1,2, 1])。计算左上角(第1行第1列)像素的卷积值时,需将卷积核旋转180°后与输入矩阵的左上角3×3区域对齐,逐元素相乘后求和:
-
(x)矩阵和(h)矩阵
-
(x)矩阵:
X = [ x [ − 1 , − 1 ] x [ 0 , − 1 ] x [ 1 , − 1 ] x [ − 1 , 0 ] x [ 0 , 0 ] x [ 1 , 0 ] x [ − 1 , 1 ] x [ 0 , 1 ] x [ 1 , 1 ] ] = [ 0 0 0 0 1 2 0 4 5 ] X=\begin{bmatrix} x[-1,-1]&x[0,-1]&x[1,-1]\\ x[-1,0]&x[0,0]&x[1,0]\\ x[-1,1]&x[0,1]&x[1,1] \end{bmatrix}=\begin{bmatrix} 0&0&0\\ 0&1&2\\ 0&4&5 \end{bmatrix} X= x[−1,−1]x[−1,0]x[−1,1]x[0,−1]x[0,0]x[0,1]x[1,−1]x[1,0]x[1,1] = 000014025
-
(h)矩阵:
H = [ h [ 1 , 1 ] h [ 1 , 0 ] h [ 1 , − 1 ] h [ 0 , 1 ] h [ 0 , 0 ] h [ 0 , − 1 ] h [ − 1 , 1 ] h [ − 1 , 0 ] h [ − 1 , − 1 ] ] = [ 1 0 − 1 2 0 − 2 1 0 − 1 ] H=\begin{bmatrix} h[1,1]&h[1,0]&h[1,-1]\\ h[0,1]&h[0,0]&h[0,-1]\\ h[-1,1]&h[-1,0]&h[-1,-1] \end{bmatrix}=\begin{bmatrix} 1&0& - 1\\ 2&0& - 2\\ 1&0& - 1 \end{bmatrix} H= h[1,1]h[0,1]h[−1,1]h[1,0]h[0,0]h[−1,0]h[1,−1]h[0,−1]h[−1,−1] = 121000−1−2−1
-
-
矩阵运算过程
- 这里计算(y[0,0])相当于计算矩阵(X)和(H)的一种特殊卷积形式(在这种小矩阵情况下类似矩阵乘法的元素对应相乘再求和),从矩阵乘法角度看,可看作是对矩阵元素对应相乘后求和。
- 按照矩阵乘法规则( C i j = ∑ k = 1 n A i k B k j C_{ij}=\sum_{k = 1}^{n}A_{ik}B_{kj} Cij=∑k=1nAikBkj)(这里(n = 3) ),对于(y[0,0]),它等于(X)和(H)对应元素乘积之和。
- 具体计算:
y [ 0 , 0 ] = X ⋅ H T = x [ − 1 , − 1 ] ⋅ h [ 1 , 1 ] + x [ 0 , − 1 ] ⋅ h [ 0 , 1 ] + x [ 1 , − 1 ] ⋅ h [ − 1 , 1 ] + x [ − 1 , 0 ] ⋅ h [ 1 , 0 ] + x [ 0 , 0 ] ⋅ h [ 0 , 0 ] + x [ 1 , 0 ] ⋅ h [ − 1 , 0 ] + x [ − 1 , 1 ] ⋅ h [ 1 , − 1 ] + x [ 0 , 1 ] ⋅ h [ 0 , − 1 ] + x [ 1 , 1 ] ⋅ h [ − 1 , − 1 ] = 0 × 1 + 0 × 2 + 0 × 1 + 0 × 0 + 1 × 0 + 2 × 0 + 0 × ( − 1 ) + 4 × ( − 2 ) + 5 × ( − 1 ) \begin{align*} y[0,0]=X \cdot\ H^T&=x[-1,-1]\cdot h[1,1]+x[0,-1]\cdot h[0,1]+x[1,-1]\cdot h[-1,1]\\ &+x[-1,0]\cdot h[1,0]+x[0,0]\cdot h[0,0]+x[1,0]\cdot h[-1,0]\\ &+x[-1,1]\cdot h[1,-1]+x[0,1]\cdot h[0,-1]+x[1,1]\cdot h[-1,-1]\\ &=0\times1 + 0\times2+0\times1+0\times0 + 1\times0+2\times0+0\times(-1)+4\times(-2)+5\times(-1) \end{align*} y[0,0]=X⋅ HT=x[−1,−1]⋅h[1,1]+x[0,−1]⋅h[0,1]+x[1,−1]⋅h[−1,1]+x[−1,0]⋅h[1,0]+x[0,0]⋅h[0,0]+x[1,0]⋅h[−1,0]+x[−1,1]⋅h[1,−1]+x[0,1]⋅h[0,−1]+x[1,1]⋅h[−1,−1]=0×1+0×2+0×1+0×0+1×0+2×0+0×(−1)+4×(−2)+5×(−1)
通过滑动卷积核(步长为1),最终得到3×3的输出特征图(图2为更直观的卷积值计算过程示意图)。


图1:标准卷积输出计算

图2:更直观的卷积值计算过程示意图
二、转置卷积的操作原理
转置卷积的核心目标是将小尺寸的特征图上采样为大尺寸特征图,其名称源于其数学本质是标准卷积的转置操作(即矩阵运算中的转置)。以下通过具体示例说明其计算过程。
假设输入特征图大小为2×2,卷积核大小为4×4,滑动步长为3,输出特征图大小可通过公式计算:
o u t = ( i n − 1 ) × s + k out = (in-1)×s + k out=(in−1)×s+k
其中,in为输入大小,s为步长,k为卷积核大小。代入数值得:
o u t = ( 2 − 1 ) × 3 + 4 = 7 out = (2-1)×3 + 4 = 7 out=(2−1)×3+4=7
即输出特征图为7×7。
转置卷积的具体步骤如下(图3为图像的转置卷积过程示意图):
- 全卷积展开:输入特征图的每个像素独立进行全卷积(即填充后卷积),每个像素生成一个4×4的特征图(大小为1+4-1=4)。输入有4个像素,因此生成4个4×4的特征图。
- 步长叠加:将4个特征图按步长3进行叠加,重叠区域的像素值相加。例如,输出的第1行第4列像素由第一个特征图的第1行第4列与第二个特征图的第1行第1列相加得到。

图3:图像的转置卷积过程
三、棋盘效应的产生与解决
转置卷积虽能有效上采样,但常伴随“棋盘效应”(Checkerboard Artifacts),即输出图像中出现类似棋盘格的不均匀色块(图4为棋盘效应示意图)。

图4:棋盘效应示意图
(一)产生原因
棋盘效应的本质是卷积核大小无法被步长整除时的不均匀重叠。以图5为例,当卷积步长为2,卷积核尺寸为3或5时,输出像素接收到的输入信息量不一致:
- 若卷积核尺寸能被步长整除(如步长2、核尺寸4),输出像素的信息重叠均匀,无棋盘效应;
- 若无法整除(如步长2、核尺寸3),相邻像素的信息重叠量不同,导致局部颜色深浅不一。

图5:卷积步长改为2时的棋盘效应示意图
(二)解决方法
为减轻或避免棋盘效应,可采用以下策略:
- 匹配核尺寸与步长:确保卷积核大小能被步长整除,例如步长2时选择核尺寸4,避免不均匀重叠;
- 使用步长1的转置卷积:步长为1时,卷积核的重叠区域均匀,可有效减少棋盘效应;
- 替代上采样方法:如采用双线性插值、最近邻插值等传统上采样方法,或结合转置卷积与像素重组(Pixel Shuffle)技术。
四、总结
转置卷积是CNN中实现上采样的重要工具,但其引入的棋盘效应需特别关注。通过理解标准卷积与转置卷积的数学本质,合理设计卷积核尺寸与步长,可有效规避棋盘效应,提升模型在语义分割、超分辨率等任务中的性能。
相关文章:

卷积神经网络进阶:转置卷积与棋盘效应详解
【内容摘要】 本文深入解析卷积神经网络中的转置卷积(反卷积)技术,重点阐述标准卷积与转置卷积的计算过程、转置卷积的上采样作用,以及其常见问题——棋盘效应的产生原因与解决方法,为图像分割、超分辨率等任务提供理论…...
重塑 Android 工程效能:2000 字终极实践指南)
用 Kotlin 脚本(KTS)重塑 Android 工程效能:2000 字终极实践指南
一、KTS 核心优势解码 1.1 类型安全革命 对比 Groovy 的动态类型缺陷,KTS 的静态类型系统能在 编译期拦截 90% 的配置错误: // Groovy 的危险操作(运行时才会报错) dependencies {implementation "com.squareup.retrofit:…...

2025年5月13日第一轮
1.百词斩 2.安全状态和死锁 3.银行家算法和状态图 4.Vue运行 5.英语听力 6.词汇 7.英语 长篇:数学竞赛 8.数学 间断点类型和数量 The rapid development of artificial intelligence has led to widerspareasd concreasns about job displacemant.As AI technology conti…...

HarmonyOs开发之———使用HTTP访问网络资源
谢谢关注!! 前言:上一篇文章主要介绍HarmonyOs开发之———Video组件的使用:HarmonyOs开发之———Video组件的使用_华为 video标签查看-CSDN博客 HarmonyOS 网络开发入门:使用 HTTP 访问网络资源 HarmonyOS 作为新一代智能终端…...
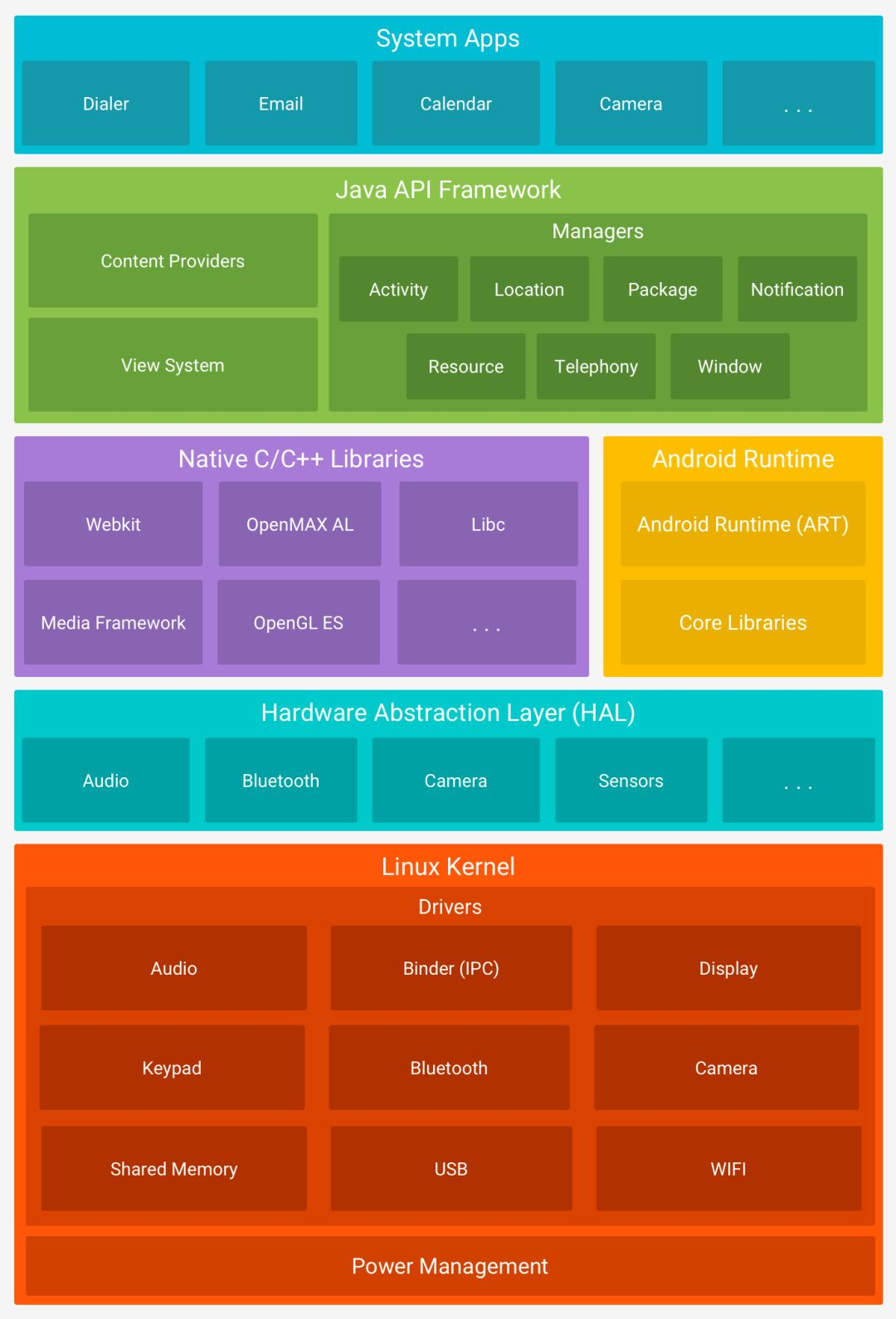
小结:Android系统架构
https://developer.android.com/topic/architecture?hlzh-cn Android系统的架构,分为四个主要层次:应用程序层、应用框架层、库和运行时层以及Linux内核层。: 1. 应用程序层(Applications) 功能:这一层包…...

单物理机上部署多个TaskManager与调优 Flink 集群
单物理机上如何高效部署与调优 Flink 集群 一、硬件环境概述 单物理机,4CPU,16G 内存,旨在充分利用硬件资源,部署 Apache Flink 集群,实现高效的分布式流处理任务。 二、Flink 集群配置 (一)配置文件说明 进入$FLINK_HOME/conf目录。备份原始配置文件:cp flink-con…...

基于C#的MQTT通信实战:从EMQX搭建到发布订阅全解析
MQTT(Message Queueing Telemetry Transport) 消息队列遥测传输,在物联网领域应用的很广泛,它是基于Publish/Subscribe模式,具有简单易用,支持QoS,传输效率高的特点。 它被设计用于低带宽,不稳定或高延迟的…...

VUE3_ref和useTemplateRef获取组件实例,ref获取dom对象
旧写法 ref的字符串需要跟js中ref定义的变量名称一样 类型丢失,无法获取到ref定义的title类型 <template><div><h1 ref"title">Hello Vue3.5</h1></div> </template><script setup>import { ref, onMounted } …...

ISP中拖影问题的处理
有时候会出现如下的阴影问题该如何处理呢?本文将提供几个思路。 1、降低曝光时间 如果曝光时间过大,会统计整个曝光时间内的图像信息,就会导致拖影的产生,这个时候可以考虑降低一下曝光时间。 2、时域降噪过大 只要明白时域降噪…...

C++.备考知识点
C++备考知识点 1. 循环结构与等差数列求和1.1 逐天累加实现方法1.2 等差数列求和公式优化2.1 数字转字符串方法2.2 首尾字符交换实现2.3 去除前导零技巧3.1 异或运算基本性质3.2 找出出现奇数次的数问题分析示例代码输出结果扩展应用4.1 字符位移量计算问题分析示例代码输出结果…...

SQLMesh 模型管理指南:从创建到验证的全流程解析
本文全面介绍SQLMesh这一现代化数据转换工具的核心功能,重点讲解模型创建、编辑、验证和删除的全生命周期管理方法。通过具体示例和最佳实践,帮助数据工程师掌握SQLMesh的高效工作流程,包括增量模型配置、变更影响评估、安全回滚机制等关键操…...

HarmonyOS AVPlayer 音频播放器
鸿蒙文档中心:使用AVPlayer播放视频(ArkTS)文档中心https://developer.huawei.com/consumer/cn/doc/harmonyos-guides/video-playback 这张图描述的是 HarmonyOS AVPlayer 音频播放器的状态流转过程,展示了 AVPlayer 在不同状态之间的切换条件和关键操作…...

⭐️白嫖的阿里云认证⭐️ 第二弹【课时1:提示词(Prompt)技巧】for 「大模型Clouder认证:利用大模型提升内容生产能力」
「大模型Clouder认证:利用大模型提升内容生产能力」这个认证目前在阿里云认证中心还是免费的,简单几步就可以申请考试,有两次的免费考试机会。而且,这个课程中的内容对于所有普通用户来说都非常实用,课程整体长度也就3节课,非常快速就能学完。心动不如行动,赶紧开始吧!…...

Filament引擎(一) ——渲染框架设计
filament是谷歌开源的一个基于物理渲染(PBR)的轻量级、高性能的实时渲染框架,其框架架构设计并不复杂,后端RHI的设计也比较简单。重点其实在于项目中材质、光照模型背后的方程式和理论,以及对它们的实现。相关的信息,可以参考官方…...

c++从入门到精通(六)--特殊工具与技术-完结篇
文章目录 特殊工具与技术-完结篇控制内存分配运行时类型识别成员指针嵌套类局部类固有的不可抑制特性位域volatile限定符链接指示 extern "C" 特殊工具与技术-完结篇 控制内存分配 重载new和delete: 如果应用程序希望控制内存分配的过程,…...

JDK 1.8 全解析:从核心特性到企业实战的深度实践
引言 JDK 1.8 作为 Java 生态发展史上的里程碑版本,自 2014 年发布以来,凭借 Lambda 表达式、Stream API、新日期时间 API 三大核心特性,彻底重塑了 Java 编程范式。本文结合 Oracle 官方文档、蚂蚁集团、京东零售等企业级实战案例ÿ…...

MCP实战:在扣子空间用扣子工作流MCP,一句话生成儿童故事rap视频
扣子最近迎来重要更新,支持将扣子工作流一键发布成MCP,在扣子空间里使用。 这个功能非常有用,因为我有很多业务工作流是在扣子平台上做的,两者打通之后,就可以在扣子空间里直接通过对话方式调用扣子工作流了࿰…...

分布式微服务系统架构第134集:笔记1运维服务器经验,高并发,大数据量系统
加群联系作者vx:xiaoda0423 仓库地址:https://webvueblog.github.io/JavaPlusDoc/ https://1024bat.cn/ https://github.com/webVueBlog/fastapi_plus https://webvueblog.github.io/JavaPlusDoc/ ✅ 一、查看端口是否被占用的常用命令 1️⃣ lsof 命令&…...

【SSL证书系列】客户端如何验证https网站服务器发的证书是否由受信任的根证书签发机构签发
客户端验证HTTPS网站证书是否由受信任的根证书颁发机构(CA)签发,是一个多步骤的过程,涉及证书链验证、信任锚(Trust Anchor)检查、域名匹配和吊销状态验证等。以下是详细的验证流程: 1. 证书链的…...

SpringBoot基础项目搭建
资料链接:https://download.csdn.net/download/ly1h1/90855288?spm1001.2014.3001.5501 1.准备工作 1.1 安装IntelliJ IDEA 2023.3.4 (Ultimate Edition) 1.2 采用apache-maven-3.6.3 1.2.1 maven配置文件设置 1.2.2 IDEA配置maven 1.3 JDK采用17版本 2.手动创建…...

Rust 学习笔记:关于 HashMap 的练习题
Rust 学习笔记:关于 HashMap 的练习题 Rust 学习笔记:关于 HashMap 的练习题以下代码能否通过编译?若能,输出是?以下代码能否通过编译?若能,输出是? Rust 学习笔记:关于 …...

C语言-8.数组
8.1数组 8.1.1初试数组 如何写一个程序计算用户输入的数字的平均数? #include<stdio.h> int main() {int digit;//输入要求平均数的数字double sum=0;//记录输入数字的和int count=0;//记录输入数字的个数printf("请输入一组数字,用来求平均数,以-1结束\n&quo…...

Kotlin Android单元测试MockK指南
目录 MockK 简介环境配置基础用法高级用法Android 特有场景最佳实践 1. MockK 简介 MockK 是一个专为 Kotlin 设计的 Mocking 框架,支持协程、扩展函数、对象声明(object)等 Kotlin 特性。相比 Mockito,它提供更自然的 Kotlin A…...

C# lock
在C#中,lock关键字用于确保当一个线程位于给定实例的代码块中时,其他线程无法访问同一实例的该代码块。这是一种简单的同步机制,用来防止多个线程同时访问共享资源或执行需要独占访问的代码段(临界区),从而…...
》阅读笔记:p83-p85)
《算法导论(第4版)》阅读笔记:p83-p85
《算法导论(第4版)》学习第 18 天,p83-p85 总结,总计 3 页。 一、技术总结 1. Strassen algorithm(施特拉森算法) 2.矩阵 (1)矩阵表示法 If we wish to refer to matrices without specifically writing out all their entries, we will use upperc…...

Go 后端中双 token 的实现模板
下面是一个典型的 Go 后端双 Token 认证机制 实现模板,使用 Gin 框架 JWT Redis,结构清晰、可拓展,适合实战开发。 项目结构建议 /utils├── jwt.go // Access & Refresh token 的生成和解析├── claims.go // 从请求…...

【拥抱AI】Deer-Flow字节跳动开源的多智能体深度研究框架
最近发现一款可以对标甚至可能超越GPT-Researcher的AI深度研究应用,Deer-Flow(Deep Exploration and Efficient Research Flow)作为字节跳动近期开源的重量级项目,正以其模块化、灵活性和人机协同能力引发广泛关注。该项目基于 La…...

第六天——贪心算法——字符串分隔
1. 题目 给定一个字符串 s,我们需要将其划分为尽可能多的部分,使得同一字母最多出现在一个部分中。 例如:字符串 "ababcc" 可以划分为 ["abab", "cc"],但要避免 ["aba", "bcc&quo…...

Python 条件语句详解
条件语句是编程中用于控制程序流程的基本结构,Python 提供了几种条件语句来实现不同的逻辑判断。 1. if 语句 最基本的条件语句形式: if 条件:# 条件为真时执行的代码块示例: age 18 if age > 18:print("你已经成年了")2. …...

前端获取用户的公网 IP 地址
可以使用免费的免费的公共服务网站 一:https://www.ipify.org/ 获取 JSON 格式的 IP 地址 // 旧地址不好使 // https://api.ipify.org/?formatjson // 新地址 https://api64.ipify.org/?formatjson 二:https://ipinfo.io/ https://ipinfo.io/ 三&a…...
