每日算法 -【Swift 算法】寻找两个有序数组的中位数(O(log(m+n)))详细讲解版
🧠 用 Swift 寻找两个有序数组的中位数(O(log(m+n)))详细讲解版
寻找两个有序数组的中位数,是 LeetCode 上非常经典的一道题,难度为 困难(Hard),但它的本质是一个 二分查找 的变形应用。
📌 题目描述
给定两个正序(从小到大)排列的数组 nums1 和 nums2,要求在 不合并数组 的前提下,找出它们的中位数,并且时间复杂度必须为 O(log(m+n))。
示例 1:
输入: nums1 = [1, 3], nums2 = [2]
合并后:[1, 2, 3]
中位数:2
示例 2:
输入: nums1 = [1, 2], nums2 = [3, 4]
合并后:[1, 2, 3, 4]
中位数:(2 + 3)/2 = 2.5
⚠️ 暴力解法(不推荐)
直接合并两个数组然后排序,再取中位数,这种做法时间复杂度是 O(m+n),不满足题目要求。
func findMedianSortedArraysBruteForce(_ nums1: [Int], _ nums2: [Int]) -> Double {// 1. 合并两个数组let merged = (nums1 + nums2).sorted()// 2. 获取总长度let count = merged.count// 3. 判断奇偶并返回中位数if count % 2 == 1 {// 奇数,直接返回中间的数return Double(merged[count / 2])} else {// 偶数,返回中间两个数的平均值let mid1 = merged[count / 2 - 1]let mid2 = merged[count / 2]return Double(mid1 + mid2) / 2.0}
}
✅ 二分查找解法(推荐)
我们要寻找的是第 k 小的数,而中位数正是数组中间的那个数。所以我们把问题转化为:
“在两个有序数组中找第 k 小的数”。
🧮 中位数转化为第 k 小数
设两个数组总长度为 total = m + n:
- 如果
total是奇数,返回第(total+1)/2小的数; - 如果
total是偶数,返回第total/2和total/2 + 1小的数的平均值。
🔧 Swift 实现(附详细注释)
func findMedianSortedArrays(_ nums1: [Int], _ nums2: [Int]) -> Double {// 获取第 k 小的元素func getKthElement(_ k: Int) -> Int {var index1 = 0, index2 = 0var k = klet m = nums1.count, n = nums2.countwhile true {// 如果 nums1 已经全部用完了,直接从 nums2 取if index1 == m {return nums2[index2 + k - 1]}// 如果 nums2 已经全部用完了,直接从 nums1 取if index2 == n {return nums1[index1 + k - 1]}// 如果 k == 1,说明我们只需要找最小的那一个if k == 1 {return min(nums1[index1], nums2[index2])}// 正常情况下,从两个数组中各取 k/2 个元素进行比较let newIndex1 = min(index1 + k / 2 - 1, m - 1)let newIndex2 = min(index2 + k / 2 - 1, n - 1)let pivot1 = nums1[newIndex1]let pivot2 = nums2[newIndex2]if pivot1 <= pivot2 {// 舍弃 nums1[index1...newIndex1]k -= (newIndex1 - index1 + 1)index1 = newIndex1 + 1} else {// 舍弃 nums2[index2...newIndex2]k -= (newIndex2 - index2 + 1)index2 = newIndex2 + 1}}}// 主逻辑let totalLength = nums1.count + nums2.countif totalLength % 2 == 1 {// 奇数时:返回中间那个数return Double(getKthElement((totalLength + 1) / 2))} else {// 偶数时:返回中间两个数的平均值let mid1 = getKthElement(totalLength / 2)let mid2 = getKthElement(totalLength / 2 + 1)return Double(mid1 + mid2) / 2.0}
}
🧪 测试代码
print(findMedianSortedArrays([1, 3], [2])) // 输出: 2.0
print(findMedianSortedArrays([1, 2], [3, 4])) // 输出: 2.5
print(findMedianSortedArrays([0, 0], [0, 0])) // 输出: 0.0
print(findMedianSortedArrays([], [1])) // 输出: 1.0
print(findMedianSortedArrays([2], [])) // 输出: 2.0
📈 时间复杂度分析
- 每次比较会排除 k/2 个元素,时间复杂度为 O(log k);
- 因为 k 最多是
m+n,所以总复杂度是 O(log(m+n)),符合要求。
✅ 总结
| 特性 | 描述 |
|---|---|
| 输入数组 | 有序 |
| 允许合并吗 | ❌ 不允许 |
| 解法 | 二分查找 |
| 时间复杂度 | O(log(m+n)) |
| 空间复杂度 | O(1) |
这种算法很有代表性,它说明了:二分查找不仅仅适用于一个数组,还可以延伸到两个数组,只要我们学会“不断舍弃不可能的部分”。
🧠 推荐练习
- LeetCode 4. Median of Two Sorted Arrays
- 寻找两个有序数组的第 K 小数
如果你觉得这篇文章对你有帮助,欢迎 👍 收藏 ⭐,评论交流 💬!
相关文章:
))详细讲解版)
每日算法 -【Swift 算法】寻找两个有序数组的中位数(O(log(m+n)))详细讲解版
🧠 用 Swift 寻找两个有序数组的中位数(O(log(mn)))详细讲解版 寻找两个有序数组的中位数,是 LeetCode 上非常经典的一道题,难度为 困难(Hard),但它的本质是一个 二分查找 的变形应…...

Linux问题排查-找到偷偷写文件的进程
在 Linux 系统中,若要通过已修改的文件找到修改该文件的进程 PID,可以结合以下方法分析,具体取决于文件是否仍被进程打开或已被删除但句柄仍存在: 一、文件仍被进程打开(未删除) 如果文件当前正在被某个进…...

SOPHGO算能科技BM1688内存使用与编解码开发指南
1. BM1688内存分配接口详解 1.1 设备内存分配接口区别 BM1688提供了三个主要的设备内存分配接口,它们的主要区别如下: // 基本设备内存分配接口 void* bm_malloc_device_byte(bm_handle_t handle, unsigned int size);// 指定heap区域的设备内存分配 void*</...

kotlin flow的两种SharingStarted策略的区别
一 两种 SharingStarted 策略的区别: SharingStarted.Eagerly: 立即开始收集上游流,即使没有下游订阅者持续保持活跃状态,直到 ViewModel 被清除优点:响应更快,数据始终保持最新缺点:消耗更多资源&#x…...
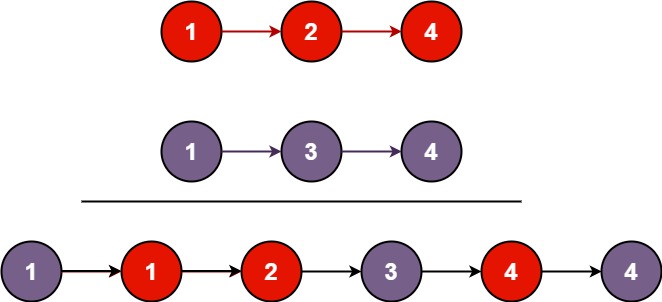
LeetCode-链表-合并两个有序链表
LeetCode-链表-合并两个有序链表 ✏️ 关于专栏:专栏用于记录 prepare for the coding test。 文章目录 LeetCode-链表-合并两个有序链表📝 合并两个有序链表🎯题目描述🔍 输入输出示例🧩题目提示🧪AC递归&…...

sqli-labs靶场29-31关(http参数污染)
目录 前言 less29(单引号http参数污染) less30(双引号http参数污染) less31(双引号括号http参数污染) 前言 在JSP中,使用request.getParameter("id")获取请求参数时,如果存在多个同名参数&a…...

独占内存访问指令LDXR/STXR
一、原子操作的介绍 在计算机领域里,如果要在多线程的情况下要保持数据的同步,需要引入称作Load-Link(LL)和Store-Conditional(SC)的操作,通常简称为LL/SC。 LL操作返回一个内存地址上当前存储…...

JVM 垃圾回收机制深度解析(含图解)
JVM 垃圾回收机制深度解析(含图解) 一、垃圾回收整体流程 垃圾回收图解 #mermaid-svg-KPtxlwWntQx8TOj3 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-KPtxlwWntQx8TOj3 .error-icon{fill…...

如何利用 Conda 安装 Pytorch 教程 ?
如何利用 Conda 安装 Pytorch 教程 ? 总共分为六步走: (1)第一步:验证conda 环境是否安装好? 1) conda -V2) conda --version(2)第二步:查看现有环境 conda env list…...

【ffmpeg】SPS与PPS的概念
PPS(Picture Parameter Set)详解 PPS(图像参数集)是H.264/H.265视频编码标准中的关键数据结构,与SPS(序列参数集)共同组成视频的解码配置信息,直接影响视频的正确解码和播放。以下是…...

uniapp vue 开发微信小程序 分包梳理经验总结
嗨,我是小路。今天主要和大家分享的主题是“uniapp vue 开发微信小程序 分包梳理经验总结”。 在使用 UniAppvue框架开发微信小程序时,当项目比较大的时候,经常需要分包加载。它有助于控制主包的大小,从而提升小程序的启…...

什么是VR展示?VR展示的用途
随着科技的迅猛发展,我们步入一个全新的数字时代。在这个时代,虚拟现实(VR)技术崭露头角,逐步改变我们对世界的认知。全景展示厅作为VR技术与传统展览艺术的完美结合,以独特的全景视角,引领我们…...

.NET外挂系列:4. harmony 中补丁参数的有趣玩法(上)
一:背景 1. 讲故事 前面几篇我们说完了 harmony 的几个注入点,这篇我们聚焦注入点可接收的几类参数的解读,非常有意思,在.NET高级调试 视角下也是非常重要的,到底是哪些参数,用一张表格整理如下ÿ…...

Go语言中new与make的深度解析
在 Go 语言中,new 和 make 是两个用于内存分配的内置函数,但它们的作用和使用场景有显著区别。 理解它们的核心在于: new(T): 为类型 T 分配内存,并将其初始化为零值,然后返回一个指向该内存的指针 (*T)。make(T, ar…...

3、ubantu系统 | 通过vscode远程安装并配置anaconda
1、vscode登录 登录后通过pwd可以发现目前位于wangqinag账号下,左侧为属于该账号的文件夹及文件。 通过cd ..可以回到上一级目录,通过ls可以查看当前目录下的文件夹及文件。 2、安装 2.1、下载anaconda 通过wget和curl下载未成功,使用手动…...

【Unity】 HTFramework框架(六十五)ScrollList滚动数据列表
更新日期:2025年5月16日。 Github 仓库:https://github.com/SaiTingHu/HTFramework Gitee 仓库:https://gitee.com/SaiTingHu/HTFramework 索引 一、ScrollList滚动数据列表二、使用ScrollList1.快捷创建ScrollList2.ScrollList的属性3.自定义…...

深度学习之用CelebA_Spoof数据集搭建一个活体检测-用MNN来推理时候如何利用Conan对软件包进行管理
我为什么用Conan 前面的文章:深度学习之用CelebA_Spoof数据集搭建一个活体检测-训练好的模型用MNN来推理有提到怎么使用MNN对训练好的模型进行推理,里面并没有提到我是怎么编译和进行代码依赖包的管理的详细步骤,在这里我是用的是Conan:一个C/C++包管理器,可以管理项目依赖…...
)
React 常见的陷阱之(如异步访问事件对象)
文章目录 前言1. 异步访问事件对象问题解决方案 2. 事件传播的误解**问题**解决方案 **3. 事件监听器未正确卸载****问题****解决方案** **4. 动态列表中的事件绑定****问题****解决方案** **5. 第三方库与 React 事件冲突****问题****解决方案** **6. 表单输入与受控组件****问…...

Swagger在java的运用
Swagger 是一个广泛使用的工具,用于设计、构建、记录和使用 RESTful Web 服务。它通过提供交互式的 API 文档、客户端 SDK 生成和 API 发现功能,极大地简化了 API 的开发和使用过程。以下是对 Swagger 的详细介绍,包括它的功能、使用场景、如…...

代码随想录算法训练营 Day49 图论Ⅰ 深度优先与广度优先
图论 基础 图的概念 图的概念 概念清单有向图 (a)无向图 (b)有向/无向如图 a 所示每条边有指向如图 b 所示每条边没有箭头指向权值每条边的权值每条边的权值度-有几条边连到该节点 (eg V 2 V_2 V2 度为 3)入度/出度出度:从该节点出发的边个数入度:…...

.NET外挂系列:1. harmony 基本原理和骨架分析
一:背景 1. 讲故事 为什么要开这么一个系列,是因为他可以对 .NET SDK 中的方法进行外挂,这种技术对解决程序的一些疑难杂症特别有用,在.NET高级调试 领域下大显神威,在我的训练营里也是花了一些篇幅来说这个…...

HarmonyOS NEXT端云一体化工程目录结构
视频课程学习报名入口:HarmonyOS NEXT端云一体化开发 端云一体化开发工程由端开发工程(Application)和云开发工程(CloudProgram)两大核心模块构成。 1)端开发工程目录结构 端开发工程主要用于开发应用端侧的业务代码,通用云开发模板的端开发工程目录结构如下图所示: …...

Ajax研究
简介 AJAX Asynchronous JavaScript and XML(异步的 JavaScript 和 XML)。 AJAX 是一种在无需重新加载整个网页的情况下,能够更新部分网页的技术。 Ajax 不是一种新的编程语言,而是一种用于创建更好更快以及交互性更强的Web应用…...

学习 Android(十)Fragment的生命周期
简介 Android 的 Fragment 是一个具有自己生命周期的 可重用 UI 组件,能够在运行时灵活地添加、移除和替换,从而支持单 Activity 多界面、动态布局和响应式设计。掌握 Fragment 的生命周期有助于正确地在各个阶段执行初始化、资源绑定、状态保存与释放操…...

flutter 常用组件详细介绍、屏幕适配方案
一、常用组件 1.基础组件 组件说明示例Text显示文本Text(‘Hello Flutter’, style: TextStyle(fontSize: 20))Image显示图片Image.network(‘https://example.com/image.jpg’)Icon显示图标Icon(Icons.home, size: 30, color: Colors.blue)RaisedButton / ElevatedButton按钮…...

Elasticsearch生产环境性能调优指南
#作者:朱雷 文章目录 一、背景二、优化项2.1. 磁盘优化2.2.配置文件优化2.3. jvm 配置2.4. 关闭或禁用 swap2.5. 最大文件描述符2.6. 段合并流量设置2.7. thread_pool相关 三、总结 一、背景 Elasticsearch是基于Lucene的开源分布式搜索与分析引擎,支持…...
从零实现用MobileFaceNet算法进行实时人脸识别(一)conda环境搭建)
野火鲁班猫(arrch64架构debian)从零实现用MobileFaceNet算法进行实时人脸识别(一)conda环境搭建
先安装miniconda wget https://repo.anaconda.com/miniconda/Miniconda3-latest-Linux-aarch64.sh chmod x Miniconda3-latest-Linux-aarch64.sh bash Miniconda3-latest-Linux-aarch64.sh source ~/.bashrc conda --version按照MobileFaceNet的github官方指南,需要…...

RT Thread FinSH(msh)调度逻辑
文章目录 概要FinSH功能FinSH调度逻辑细节小结 概要 RT-Thread(Real-Time Thread)作为一款开源的嵌入式实时操作系统,在嵌入式设备领域得到了广泛应用。 该系统不仅具备强大的任务调度功能,还集成了 FinSH命令行系统,…...
)
Kotlin 极简小抄 P9 - 数组(数组的创建、数组元素的访问与修改、数组遍历、数组操作、多维数组、数组与可变参数)
Kotlin 概述 Kotlin 由 JetBrains 开发,是一种在 JVM(Java 虚拟机)上运行的静态类型编程语言 Kotlin 旨在提高开发者的编码效率和安全性,同时保持与 Java 的高度互操作性 Kotlin 是 Android 应用开发的首选语言,也可…...

CSS display有几种属性值
在 CSS 中,display 属性是控制元素布局和渲染方式的核心属性之一。它有多种属性值,每个值都决定了元素在文档流中的表现形式。以下是 display 的主要属性值分类及说明: 1. 块级和行内布局 块级元素 (block) 特性:独占一行&…...
