哈希表的实现(上)
前言
在C++98中,STL提供了底层为红黑树结构的一系列关联式容器,在查询时效率可达到,即最差情况下需要比较红黑树的高度次,当树中的节点非常多时,查询效率也不理想。最好的查询是,进行很少的比较次数就能够将元素找到,因此在C++11中,STL又提供了4个unordered系列的关联式容器,这四个容器与红黑树结构的关联式容器使用方式基本类似,只是其底层结构不同,分别unordered_map、unordered_set和unordered_multimap、unordered_multiset。他们的底层便用到了哈希表。本文将从哈希表的基本实现、封装、迭代器的实现、const迭代器的实现顺序进行介绍。
哈希
引入
在介绍前,我们先来做一道简单的题目,这种思想就用到了哈希。
387. 字符串中的第一个唯一字符 - 力扣(LeetCode)

此题可以用暴力查找,一遍一遍的统计每个字母的个数,但这种方法时间复杂度太大了。直接说优化方法,我们可以把每个字母和数组的下标进行映射,我们知道每个字符都可以通过assic转换为一个数,比如'a'这个字母,只要将他在减去一个'a',那么得到的就是0,我们开一个int数组,大小为26,这样刚好存入26个英文字母。这样只需要遍历一遍字符串,便可以把所有的字母都统计一遍,然后在遍历一遍,就能得到哪个出现了一次。代码如下:
class Solution {
public:int firstUniqChar(string s) {vector<int> arr(26);for(int i = 0;i<s.size();i++){arr[s[i]-'a']++;}for(int i = 0;i<s.size();i++){if(arr[s[i]-'a']==1)return i;}return -1;}
};通过assic的转换与数组下标取得映射关系,这种思想就用到了哈希,接下来我们就详细介绍一下哈希。
哈希概念
顺序结构以及平衡树中,元素关键码与其存储位置之间没有对应的关系,因此在查找一个元素
时,必须要经过关键码的多次比较。顺序查找时间复杂度为O(N),平衡树中为树的高度,即
O(),搜索的效率取决于搜索过程中元素的比较次数。
理想的搜索方法:可以不经过任何比较,一次直接从表中得到要搜索的元素。如果构造一种存储结构,通过某种函数使元素的存储位置与它的关键码之间能够建立一一映射的关系,那么在查找时通过该函数可以很快找到该元素。

用该方法进行搜索不必进行多次关键码的比较,因此搜索的速度比较快。
但这样就会有一个问题,当我们插入11或者14时就会出现多个数值映射一个位置的情况。就是哈希冲突
哈希冲突
原因
出现上面的情况有以下几种原因:
- 哈希函数设计不合理:如果哈希函数不能将键均匀地分布到哈希表的各个位置,就会导致某些位置被频繁访问,从而增加冲突的概率。
- 哈希表大小有限:哈希表的大小是有限的,而键的数量可能是无限的。当键的数量超过哈希表的大小时,冲突就不可避免。
- 键的分布不均匀:如果键的分布本身就不均匀,那么即使哈希函数设计得再好,也无法完全避免冲突。
解决方法
enum Status{EMPTY,EXIST,DELETE};接下来我们在实现一个节点
template<class K, class V>struct HashData{pair<K, V> _kv;Status _s; //状态};
暂时先实现为KV结构,后面会更改。
接下来是最基本的哈希表结构。
class HashTable{public:HashTable(){_tables.resize(10);}private:vector<HashData> _tables;size_t _n = 0; // 存储的关键字的个数};
}定义一个vector<HashData>类型的数组,在定义一个_n表示存储关键字的数量,构造函数中先给vector开十个大小的空间。之后我们来进行插入操作。
Insert
插入操作时,我们需要规定一个负载因子,它表示的是该空间中非空所占空间的比例,如果超出这个值就需要扩容,通常设置为0.7比较合适。(设计太大,那么产生冲突的可能性就越大,但相对于来说节省点空间,设计太小,产生冲突可能性小,但浪费了大量空间)代码如下:
bool Insert(const pair<K, V>& kv){// 负载因子0.7就扩容if (_n*10 / _tables.size() == 7){size_t newSize = _tables.size() * 2;HashTable<K, V> newHT;newHT._tables.resize(newSize);// 遍历旧表for (size_t i = 0; i < _table.size(); i++){if (_tables[i]._s == EXIST){newHT.Insert(_tables[i]._kv);}}_tables.swap(newHT._tables);}size_t hashi = kv.first % _tables.size();while (_tables[hashi]._s == EXIST){hashi++;hashi %= _tables.size();}_tables[hashi]._kv = kv;_tables[hashi]._s = EXIST;++_n;return true;}首先先判断负载因子的大小,若超过则进行扩容处理,扩容的大小为之前的二倍,然后构建一个新的哈希表,在新的哈希表中重新插入原表中的值,之后再用swap进行交换,这样我们就完成了扩容。不用担心新建的哈希表无法释放,他会自动调用vector的析构函数。
扩完容或者不需要扩容时,进行下一步操作,通过哈希函数找到位置,进行插入,如果该位置已经存在,就接着向下查找,直到出现空或者删除状态时再进行插入。插入成功后把该位置的状态改为EXIST,并++n。这就是insert的实现。
Find
比如我们查找44,首先算出他的关键值4,那么在他的位置进行查找时,不为空,但他里面存放的并不是44,这时我将就继续向下寻找,在下表为8处找到了他。
如果我们查找34,关键值还是4,但当我们一直查找直到下表为0时,状态为空,此时结束,就说明没有34这个数。

还有一种情况,当我们把6删除时,应该为伪删除,也就是 不是真的把6去掉,而是将6位置的状态设置为删除,删除后当我们在查找6时,发现它的状态为删除,那么我们也无法找到。
代码如下:
HashData<K, V>* Find(const K& key){size_t hashi = key % _tables.size();while (_tables[hashi]._s != EMPTY){if (_tables[hashi]._s == EXIST&& _tables[hashi]._kv.first == key){return &_tables[hashi];}hashi++;hashi %= _tables.size();}return NULL;}Erase
bool Erase(const K& key){HashData<K, V>* ret = Find(key);if (ret){ret->_s = DELETE;--_n;return true;}else{return false;}}删除时我们要先确定这个值在不在,若不存在直接返回false,若存在进行删除操作。
将该位置的状态改为删除,并且--n遍完成了操作。
相关文章:

哈希表的实现(上)
前言 在C98中,STL提供了底层为红黑树结构的一系列关联式容器,在查询时效率可达到,即最差情况下需要比较红黑树的高度次,当树中的节点非常多时,查询效率也不理想。最好的查询是,进行很少的比较次数就能够将…...

【Java高阶面经:微服务篇】1.微服务架构核心:服务注册与发现之AP vs CP选型全攻略
一、CAP理论在服务注册与发现中的落地实践 1.1 CAP三要素的技术权衡 要素AP模型实现CP模型实现一致性最终一致性(Eureka通过异步复制实现)强一致性(ZooKeeper通过ZAB协议保证)可用性服务节点可独立响应(支持分区存活)分区期间无法保证写操作(需多数节点可用)分区容错性…...

实验7 HTTP协议分析与测量
实验7 HTTP协议分析与测量 1、实验目的 了解HTTP协议及其报文结构 了解HTTP操作过程:TCP三次握手、请求和响应交互 掌握基于tcpdump和wireshark软件进行HTTP数据包抓取和分析技术 2、实验环境 硬件要求:阿里云云主机ECS 一台。 软件要求࿱…...

python:机器学习概述
本文目录: 一、人工智能三大概念二、学习方式三、人工智能发展史**1950-1970****1980-2000****2010-2017****2017-至今** 四、机器学习三要素五、常见术语六、数据集的划分七、常见算法分类八、机器学习的建模流程九、特征工程特征工程包括**五大步**:特…...

【一. Java基础:注释、变量与数据类型详解】
1. Java 基础概念 1.1 注释 注释:对代码的解释和说明文字 java的三种注释: 单行注释:两个斜杠 // 后面跟着你的注释内容 //哈哈多行注释:以 /* 开头,以 */ 结尾,中间可以写很多行 /*哈哈哈哈哈哈…...

得力DE-620K针式打印机打印速度不能调节维修一例
基本参数: 产品类型 票据针式打印机(平推式) 打印方式 串行点阵击打式 打印宽度 85列 打印针数 24针 可靠性 4亿次/针 色带性能 1000万字符纠错 复写能力 7份(1份原件+6份拷贝) 缓冲区 128KB 接口类型 …...

SAP在金属行业的数字化转型:无锡哲讯科技的智能解决方案
金属行业面临的发展挑战 金属行业作为制造业的基础支柱,涵盖钢铁、有色金属、金属制品等多个细分领域。当前行业正面临原材料价格波动、能耗双控政策、市场竞争加剧等多重压力。数字化转型已成为金属企业提升生产效率、优化供应链、实现绿色可持续发展的必由之路。…...

安装openresty使用nginx+lua,openresty使用jwt解密
yum install -y epel-release yum update yum search openresty # 查看是否有可用包 yum install -y openresty启动systemctl start openresty验证服务状态systemctl status openresty设置开机自启systemctl enable openrestysystemctl stop openresty # 停止服务 system…...

java基础(继承)
什么是继承 继承好处 提高代码的复用性 继承注意事项 权限修饰符 单继承、Object类 冲突: 方法重写 扩展: 其实我们不想看地址,地址看来没用,我们是用来看对象有没有问题 重写toString: 比如这个如果返回的是地址值,…...

python 实现一个完整的基于Python的多视角三维重建系统,包含特征提取与匹配、相机位姿估计、三维重建、优化和可视化等功能
多视角三维重建系统 下面我将实现一个完整的基于Python的多视角三维重建系统,包含特征提取与匹配、相机位姿估计、三维重建、优化和可视化等功能。 1. 环境准备与数据加载 首先安装必要的库: pip install opencv-python opencv-contrib-python numpy…...

行列式中某一行的元素与另一行对应元素的代数余子式乘积之和等于零
问题陈述 为什么行列式中某一行(列)的元素与另一行(列)对应元素的代数余子式乘积之和等于零?即: ∑ k 1 n a i k C j k 0 ( i ≠ j ) \sum_{k1}^{n} a_{ik} C_{jk} 0 \quad (i \ne j) k1∑naikCjk…...

【时时三省】Python 语言----字符串,列表,元组,字典常用操作异同点
目录 1,字符串常用操作 1,创建 2,访问 3,常用方法 4,内置方法 2,列表 1,创建列表 2,访问列表 3,内置方法 3,元组 1,创建 2,访问 3,内置方法 4,字典 1,创建 2,访问 3,内置方法 5,集合 1,创建 2,访问 3,内置方法 山不在高,有仙则名。水不在深,有龙则…...

基于cornerstone3D的dicom影像浏览器 第二十二章 mpr + vr
系列文章目录 第一章 下载源码 运行cornerstone3D example 第二章 修改示例crosshairs的图像源 第三章 vitevue3cornerstonejs项目创建 第四章 加载本地文件夹中的dicom文件并归档 第五章 dicom文件生成png,显示检查栏,序列栏 第六章 stack viewport 显…...

优启通添加自定义浏览器及EXLOAD使用技巧分享
文章目录 优启通添加自定义浏览器及EXLOAD使用技巧分享🚩问题描述🔧解决方案概述📁自定义软件添加方法汇总🧩快捷方式配置:exload.cfg 用法大全🧷基础用法🗂分类菜单🖥创建桌面快捷方…...

MySQL:游标 cursor 句柄
当我们select * from emp 可以查看所有的数据 这个数据就相当于一个数据表 游标的作用相当于一个索引 一个指针 指向每一个数据 假设说我要取出员工中薪资最高的前五名成员 就要用到limit关键字 但是这样太麻烦了 所以这里用到了游标 游标的声明: declare my…...

二、ZooKeeper 集群部署搭建
作者:IvanCodes 日期:2025年5月24日 专栏:Zookeeper教程 我们这次教程将以 hadoop01 (192.168.121.131), hadoop02 (192.168.121.132), hadoop03 (192.168.121.133) 三台Linux服务器为例,搭建一个ZooKeeper 3.8.4集群。 一、下载…...
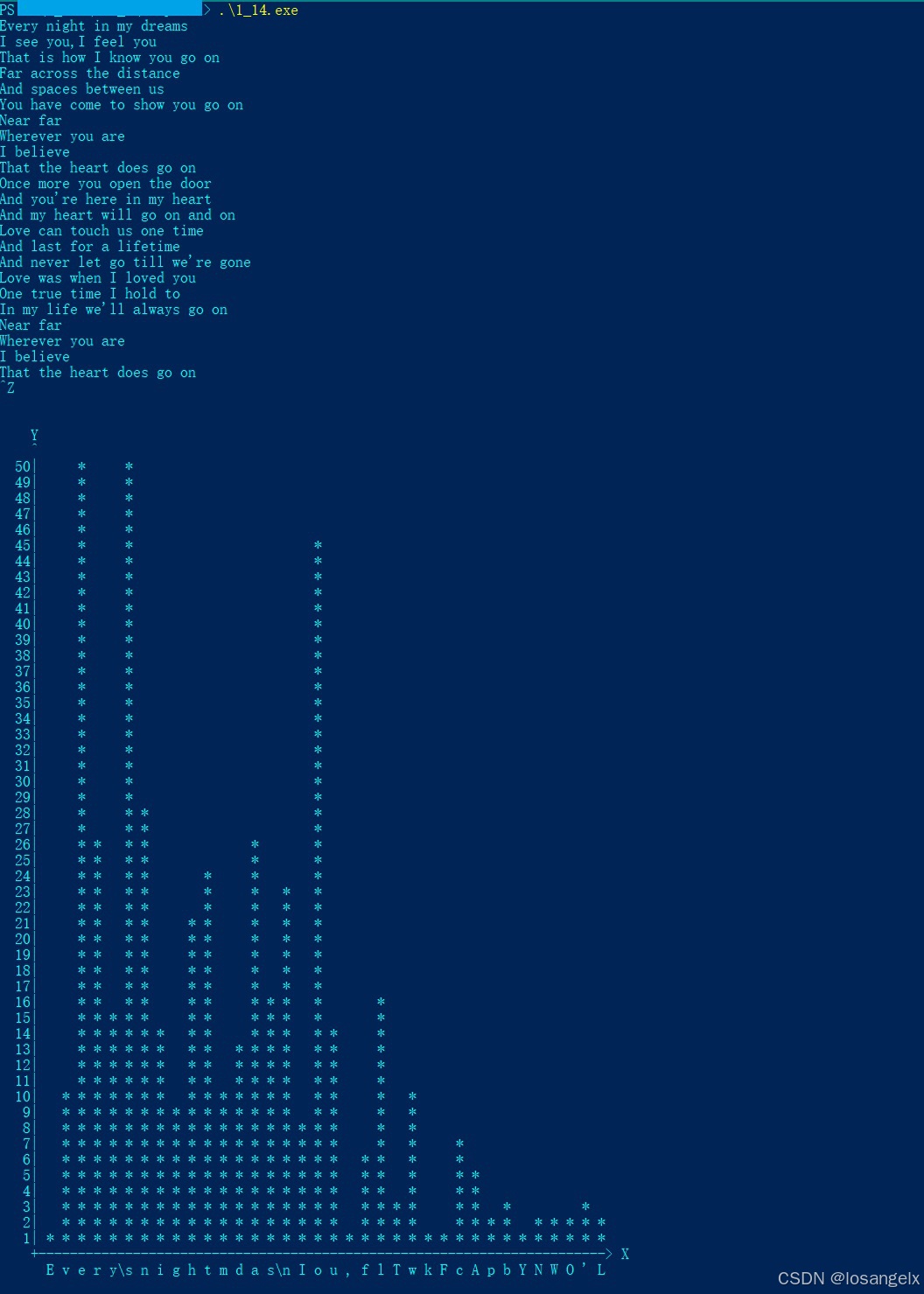
<< C程序设计语言第2版 >> 练习1-14 打印输入中各个字符出现频度的直方图
1. 前言 本篇文章是<< C程序设计语言第2版 >> 的第1章的编程练习1-14, 个人觉得还有点意思, 所以写一篇文章来记录下. 希望可以给初学C的同学一点参考. 尤其是自学的同学, 或者觉得以前学得不好, 需要自己补充学习的同学. 和我的很多其它文章一样, 不建议自己还没实…...

黑马点评双拦截器和Threadlocal实现原理
文章目录 双拦截器ThreadLocal实现原理 双拦截器 实现登录状态刷新的原因: 防止用户会话过期:通过动态刷新Token有效期,确保活跃用户不会因固定过期时间而被强制登出 提升用户体验:用户无需频繁重新登录,只要…...

港股IPO市场火爆 没有港卡如何参与港股打新?
据Wind资讯数据统计,今年1月1日至5月20日,港股共有23家企业IPO,较去年同期增加6家;IPO融资规模达600亿港元,较去年同期增长626.54%,IPO融资规模重回全球首位。 港股IPO市场持续火爆,不少朋友没有…...
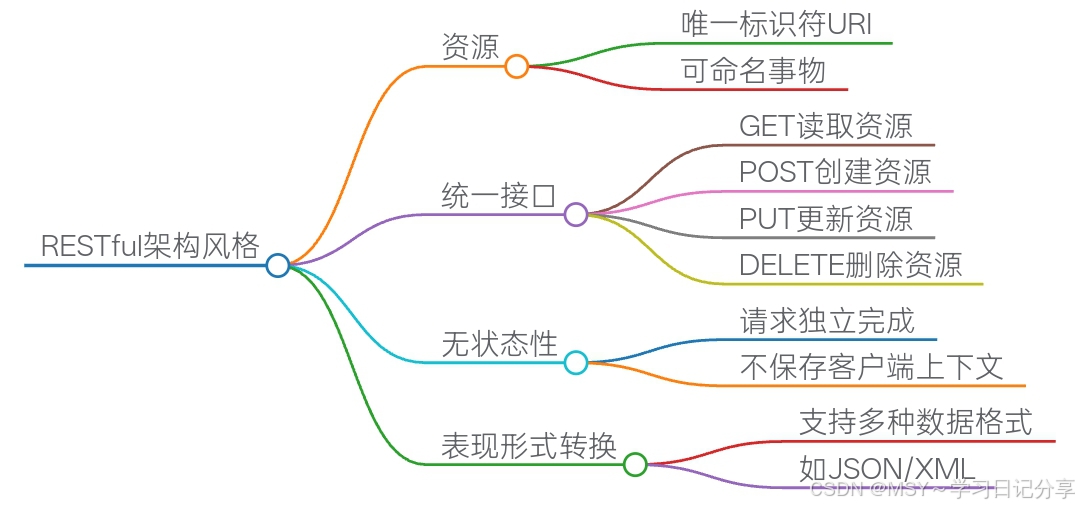
RESTful API 在前后端交互中的作用与实践
一、RESTful API 概述 RESTful(Representational State Transfer)API 是一种基于 HTTP 协议、面向资源的架构风格,旨在实现前后端的松散耦合和高效通信。它通过定义统一的资源标识、操作方法以及数据传输格式,为前后端提供了一种…...

Jenkins+Docker+Harbor快速部署Spring Boot项目详解
JenkinsDockerHarbor快速部署Spring Boot项目详解 Jenkins、Docker和Harbor是现代DevOps流程中的核心工具,结合使用可以实现自动化构建、测试和部署。下面我将详细介绍如何搭建这个集成环境。 一、各工具的核心作用 Jenkins 自动化CI/CD工具,负责拉取代…...

python打卡训练营打卡记录day35
知识点回顾: 三种不同的模型可视化方法:推荐torchinfo打印summary权重分布可视化进度条功能:手动和自动写法,让打印结果更加美观推理的写法:评估模式 作业:调整模型定义时的超参数,对比下效果 1…...

如何评价OpenRouter这样的大模型API聚合平台?
OpenRouter通过统一接口简化多模型访问与集成的复杂性,实现一站式调用。然而,这种便利性背后暗藏三重挑战:成本控制、服务稳定性、对第三方供应商的强依赖性。 现在AI大模型火得一塌糊涂,新模型层出不穷,各有各的长处。但是对于开发者来说,挨个去对接OpenAI、谷歌、Anthr…...

恢复二叉搜索树:递归与中序遍历的智慧应用
恢复二叉搜索树:递归与中序遍历的智慧应用 二叉搜索树(BST)是一种在算法世界里相当重要的数据结构,它的特性——左子树的节点值小于根节点,而右子树的节点值大于根节点——让它在查找、插入和删除操作上都能高效运行。然而,现实总是充满意外,有时候由于错误的操作或数据…...

从零开始构建一个区块链应用:技术解析与实践指南
区块链技术自比特币诞生以来,已经逐渐从金融领域扩展到更多行业,如供应链管理、物联网、智能合约等。它以其去中心化、不可篡改和透明性等特点,吸引了众多开发者的关注。然而,对于初学者来说,区块链技术的学习曲线可能…...

5.2.4 wpf中MultiBinding的使用方法
在 WPF 中,MultiBinding 允许将多个绑定(Binding)组合成一个逻辑结果,并通过一个转换器(IMultiValueConverter)处理这些值,最终影响目标属性。以下是其核心用法和示例: 核心组件: MultiBinding:定义多个绑定源的集合。 IMultiValueConverter:实现逻…...

技术服务业-首套运营商网络路由5G SA测试专网搭建完成并对外提供服务
为了更好的服务蜂窝无线技术及运营商测试认证相关业务,搭建了技术服务业少有的5G测试专网,可独立灵活配置、完整端到端5G(含RedCap、LAN)的网络架构。 通过走真正运营商网络路由的方式,使终端设备的测试和运营商网络兼…...

仿腾讯会议——音频服务器部分
1、中介者定义处理音频帧函数 2、 中介者实现处理音频帧函数 3、绑定函数映射 4、服务器定义音频处理函数 5、 服务器实现音频处理函数...

大文件上传,对接阿里oss采用前端分片技术。完成对应需求!
最近做了一个大文件分片上传的功能,记录下 1. 首先是安装阿里云 oss 扩展 composer require aliyuncs/oss-sdk-php 去阿里云 oss 获取配置文件 AccessKey ID *** AccessKey Secret *** Bucket名称 *** Endpoint *** 2. 前端上传,对文件进行分片…...

【场景分析】基于概率距离快速削减法的风光场景生成与削减方法
目录 1 主要内容 场景消减步骤 2 部分代码 3 程序结果 1 主要内容 该程序参考文献《含风光水的虚拟电厂与配电公司协调调度模型》场景消减部分模型,程序对风电场景进行生成并采用概率距离方法进行消减,程序先随机生成200个风电出力场景,然…...
