「EMD/EEMD/VMD 信号分解方法 ——ECG信号处理-第十四课」2025年5月23日
一、引言
上一节,我们介绍了希尔伯特黄变换(HHT)及其经验模态分解(EMD)的相关内容,这一节,我们继续拓展EMD分解技术,补充介绍集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)和变分模态分解(Variational Mode Decomposition,VMD)分解方法。
二、3种信号分解方法
2.1 经验模态分解(Empirical Mode Decomposition,EMD)
经验模态分解(Empirical Mode Decomposition,EMD),它能够将复杂的非平稳信号分解为若干个本征模态函数(Intrinsic Mode Functions,IMFs)。IMFs反映了信号在不同时间尺度上的局部特征。EMD分解过程是基于信号的局部极值点,通过不断筛选出信号中的局部极值点来构造上下包络线,从而得到各个IMFs。这一过程是自适应的,不需要预先设定信号的模型,能够很好地适应心电信号的非平稳特性。

图1 经验模态分解示意图
2.1.1. IMF的定义
一个本征模态函数(IMF)必须满足以下两个条件:
-
在整个数据段内,极值点(极大值点和极小值点)的数量和过零点的数量必须相等,或者最多相差一个。
-
在任意时刻,由局部极大值点定义的上包络和由局部极小值点定义的下包络的平均值为零。
2.1.2 EMD分解步骤
EMD分解过程可以分为以下几个步骤:
(1)寻找局部极值点
-
对于给定的信号 s(t),首先找到所有的局部极大值点和极小值点。局部极大值点是指在该点及其邻域内,信号值达到局部最大值;局部极小值点是指在该点及其邻域内,信号值达到局部最小值。
(2)构造上下包络线
- 使用三次样条插值方法,通过局部极大值点构造上包络线 Eupper(t),通过局部极小值点构造下包络线 Elower(t)。包络线的构造公式如下:


(3)计算均值
-
计算上下包络线的均值 m(t):

(4)筛选过程
-
从原始信号中减去均值 m(t),得到新的信号 h(t):
![]()
-
检查 h(t) 是否满足IMF的条件。如果满足,则 h(t) 是一个IMF;如果不满足,则将 h(t) 作为新的信号,重复上述步骤,直到满足IMF的条件。
(5)分解IMFs
-
重复上述过程,从原始信号中逐步提取出各个IMF。每次提取一个IMF后,从原始信号中减去该IMF,得到剩余信号,然后对剩余信号继续进行EMD分解,直到剩余信号不再包含任何IMF为止。
2.1.3 EMD分解的数学表示
假设原始信号为 s(t),通过EMD分解可以得到 n 个IMF和一个残差 r(t):
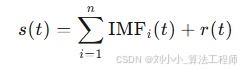
其中,IMFi(t) 表示第 i 个本征模态函数,r(t) 是分解后的残差,包含信号的低频趋势或噪声成分。
2.2 集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)
2.2.1 EEMD分解步骤
EEMD 是 EMD 的改进方法,通过在原始信号中添加白噪声来解决模态混叠问题。其步骤如下:
-
向原始信号 x(t) 添加白噪声:xnoisy(t)=x(t)+noise(t)。
-
对加噪信号 xnoisy(t) 进行 EMD 分解,得到一组 IMF 分量 {ci,j(t)},其中 i 表示第 i 个 IMF 分量,j 表示第 j 次加噪。
-
重复上述过程 N 次。
-
对 N 次分解得到的 IMF 分量进行集合平均,得到最终的 IMF 分量:

2.2.2 EEMD的数学表述
EEMD 分解可以表示为:
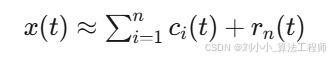
其中,ci(t) 是通过集合平均得到的第 i 个 IMF 分量,rn(t) 是最终残差。
2.3 变分模态分解(Variational Mode Decomposition,VMD)
2.3.1 目标函数构建
变分模态分解(VMD)是一种基于变分优化框架的自适应信号分解方法,旨在将复杂信号分解为多个具有稀疏频带特性的本征模态函数(Band-Limited Intrinsic Mode Functions, BLIMFs)。其核心思想是通过数学优化手段,在频域内自适应地划分信号频谱,从而克服传统经验模态分解(EMD)的模态混叠和端点效应问题。
VMD的核心是构造一个约束优化问题,要求每个模态函数 uk(t) 的带宽最小化,同时保证所有模态的线性组合等于原始信号 f(t) 。其数学模型为:

物理意义:
-
∂t表示时间导数:约束每个模态的瞬时变化特性。
-
Hilbert变换项 (δ(t)+jπt)∗uk(t):将模态转换为解析信号,便于频域分析。
-
指数项 e^−jωkt:将模态的频谱搬移到基带,简化带宽计算。
-
目标函数最小化:迫使每个模态 uk(t)的能量集中在以 ωk 为中心的窄带内。
2.3.2 约束条件的松弛化
为便于求解,引入拉格朗日乘子 λ(t) 和二次惩罚项,将原约束优化问题转化为无约束形式:

其中:
-
α:带宽约束因子,控制模态的带宽(α 越大,模态带宽越窄)。
-
二次惩罚项:增强算法对噪声的鲁棒性。
2.3.3 交替方向乘子法(ADMM)求解
通过交替方向乘子法(ADMM)迭代更新模态 uk、中心频率 ωk,以及拉格朗日乘子 λλ。
(1) 模态更新(频域形式)
在频域中,模态函数的更新方程为:

-
将时域信号转换至频域,简化微分运算。
-
通过引入拉格朗日乘子的频域形式 λ^(ω) ,分离各模态的耦合。
-
分母项 1+2α(ω−ωk)^2 体现带宽约束,迫使能量集中在 ωk 附近。
(2) 中心频率更新
中心频率 ωk 通过能量重心法更新:

新的中心频率是模态功率谱的加权平均,确保每个模态的频谱能量集中在其中心频率附近。
(3) 拉格朗日乘子更新
拉格朗日乘子用于强制约束条件的满足:

其中 τ (tao)为更新步长(噪声容忍参数),控制收敛速度。
(4)模态数 K
-
选择依据:根据信号的频谱特征预先设定。若 K 过小,导致模态欠分解;若 K 过大,引入虚假模态。
-
心电信号建议:通常取 K=6∼10,覆盖QRS波(高频)、P/T波(中频)、基线漂移(低频)。
三、EEMD和VMD在心电信号特征提取中的应用
3.1 实验过程
通过对心电信号进行EMD/EEMD/VMD分解,我们得到了多个IMF。每个IMF代表了心电信号的一个局部特征,可以用于进一步的分析和诊断。以下是具体的实验结果和分析:
-
图2展示了原始心电信号的波形,可以看出心电信号的周期性和波动性。

图2 原始心电信号(mitdb-222号记录)
3.1.1 EMD分解结果
-
图3展示了EMD分解后的9个IMF。每个IMF代表了心电信号的一个局部特征,可以用于进一步的分析和诊断。

图3 EMD分解(mitdb-222号记录)
-
图4展示了EMD分解结果的小窗显示,通过偏移量区分不同的IMF,便于观察和比较。

图4 EMD分解的偏移量小窗显示(mitdb-222号记录)
(3)IMF的瞬时频率
-
图5展示了IMF2的瞬时频率。瞬时频率的变化可以反映心电信号的动态特性,有助于识别心电信号中的异常特征。

图5 EMD-IMF2的瞬时频率(mitdb-222号记录)
3.1.2 EEMD分解结果
选择噪声系数为0.2,迭代次数为100,进行EEMD分解,结果如下所示。

图6 EEMD分解(mitdb-222号记录)

图7 EEMD分解的偏移量小窗显示(mitdb-222号记录)

图8 EEMD-IMF2的瞬时频率(mitdb-222号记录)
3.1.3 VMD分解结果
选择如下参数,对原始心电信号进行VMD分解,结果如下所示。
%--------- 对于VMD参数进行设置---------------
alpha = 2000; % moderate bandwidth constraint:适度的带宽约束/惩罚因子
tau = 0.0244; % noise-tolerance (no strict fidelity enforcement):噪声容限(没有严格的保真度执行)
K = 10; % modes:分解的模态数
DC = 0; % no DC part imposed:无直流部分
init = 1; % initialize omegas uniformly :omegas的均匀初始化

图9 VMD分解(mitdb-222号记录)

图10 VMD分解的偏移量小窗显示(mitdb-222号记录)

图11 VMD-IMF2的瞬时频率(mitdb-222号记录)
四、实验结果与分析
(一)EEMD/VMD 在心电信号特征提取中的优势
-
EEMD 的优势 (1)通过添加白噪声,解决了传统 EMD 中的模态混叠问题,提高了分解结果的稳定性和可靠性。 (2)能够自适应地分解心电信号中的多频率成分,提取出不同频率段的特征信息,有助于更准确地分析心电信号的时频特性。
-
VMD 的优势 (1)在分解过程中能够自适应地确定模态函数的中心频率和带宽,避免了传统 EMD 方法中存在的端点效应问题。 (2)通过优化模型实现信号分解,分解结果更加合理且具有物理意义,能够更好地反映心电信号的内在结构。
(二)EEMD 和 VMD 分解结果比较
-
分解效果: EEMD 和 VMD 都能有效地将心电信号分解为多个分量。EEMD 的分解结果受白噪声影响,具有一定的随机性;VMD 的分解结果更稳定,且无模态混叠。
-
计算效率: VMD 可并行实现,计算效率高于 EEMD。
-
适用场景: 对于需要精确特征提取的场景,VMD 更适用;对于对随机性有一定容忍度的场景,EEMD 也能取得较好的效果。
通过实验验证了 EEMD 和 VMD 在心电信号特征提取中的有效性。实验数据为从 222.dat 文件中读取的心电信号,采样频率为 360 Hz。分别采用 EEMD 和 VMD 方法对心电信号进行分解,得到多个 IMF 分量,并绘制了分解结果的大窗图和小窗图。从分解结果可以看出,两种方法都能够有效地将心电信号分解为多个具有不同频率特性的 IMF 分量。进一步对 IMF 分量进行功率谱密度分析和瞬时频率计算,提取了心电信号的特征信息,为心律失常检测等应用提供了基础。
Tips:下一讲,我们将进一步探讨,心电信号特征提取——傅里叶变换谱、小波谱与希尔伯特谱分析等。
以上就是EMD/EEMD/VMD 信号分解方法的全部内容啦~
我们下期再见,拜拜(⭐v⭐) ~
(Ps:有代码实现需求,请见主页信息,谢谢支持!~)
相关文章:

「EMD/EEMD/VMD 信号分解方法 ——ECG信号处理-第十四课」2025年5月23日
一、引言 上一节,我们介绍了希尔伯特黄变换(HHT)及其经验模态分解(EMD)的相关内容,这一节,我们继续拓展EMD分解技术,补充介绍集合经验模态分解(Ensemble Empirical Mode …...

二叉树层序遍历6
INT_MIN的用法: INT_MIN是C/C 中的一个宏常量 ,在 <limits.h> (C 中也可使用 <climits> )头文件中定义,代表 int 类型能表示的最小整数值 。其用法主要体现在以下方面: 1.初始化变量 …...

【论文精读】2023 AAAI--FastRealVSR现实世界视频超分辨率(RealWorld VSR)
文章目录 一、摘要二、Method2.1 现象(问题)--对应文中隐状态的分析(Analysis of Hidden State)2.2 怎么解决 --对应文中Framework2.2.1 整体流程:2.2.2 HSA模块怎么工作?2.2.2.1 隐藏状态池2.2.2.2 选择性…...

IPython 常用魔法命令
文章目录 IPython 魔法命令(Magic Commands)一、系统与文件操作1. %ls2. %cd和%pwd3. %%writefile4. %run 二、性能分析与计时1. %timeit2. %prun3. %%timeit 三、代码处理与交互1. %load2. %edit3. %store 四、调试与诊断2. …...

数据同步自动化——如何用Python打造高效工具?
友友们好! 我是Echo_Wish,我的的新专栏《Python进阶》以及《Python!实战!》正式启动啦!这是专为那些渴望提升Python技能的朋友们量身打造的专栏,无论你是已经有一定基础的开发者,还是希望深入挖掘Python潜力的爱好者,这里都将是你不可错过的宝藏。 在这个专栏中,你将会…...

开源与闭源之争:AI时代的创新博弈与未来抉择
在人工智能技术狂飙突进的今天,开源与闭源之争已不再局限于技术圈的讨论,而是演变为一场关乎技术伦理、商业格局乃至人类文明走向的深度博弈。当Meta的Llama 3开源模型下载量突破百万,当OpenAI的GPT-5继续加固技术壁垒,这场没有硝…...

flutter dart class语法说明、示例
🔹 Dart 中的 class 基本语法 class ClassName {// 属性(字段)数据类型 属性名;// 构造函数ClassName(this.属性名);// 方法返回类型 方法名() {// 方法体} }✅ 示例:创建一个简单的 Person 类 class Person {// 属性String name;…...

Java虚拟机 - 程序计数器和虚拟机栈
运行时数据结构 Java运行时数据区程序计数器为什么需要程序计数器执行流程虚拟机栈虚拟机栈作用虚拟机栈核心结构运行机制 Java运行时数据区 首先介绍Java运行时数据之前,我们要了解,对于计算机来说,内存是非常重要的资源,因为内…...
)
SpringMVC04所有注解按照使用位置划分| 按照使用层级划分(业务层、视图层、控制层)
目录 一、所有注解按照使用位置划分(类、方法、参数) 1. 类级别注解 2. 方法级别注解 3. 参数级别注解 4. 字段/返回值注解 二、按照使用层级划分(业务层、视图层、控制层) 1、控制层(Controller Layer&#x…...

新能源汽车产业链图谱分析
1. 产业定义 新能源汽车是指采用非常规的车用燃料作为动力来源,综合车辆的动力控制和驱动方面的先进技术,形成的具有新技术、新结构、技术原理先进的汽车。 新能源车包括四大类型:混合动力电动汽车(HEV)、纯电动汽车…...

如何在PyCharm2025中设置conda的多个Python版本
前言 体验的最新版本的PyCharm(Community)2025.1.1,发现和以前的版本有所不同。特别是使用Anaconda中的多个版本的Python的时候。 关于基于Anaconda中多个Python版本的使用,以及对应的Pycharm(2023版)的使用,可以参考…...
算法详解:图解+代码+经典例题)
005 深度优先搜索(DFS)算法详解:图解+代码+经典例题
📌 什么是深度优先搜索? 深度优先搜索(Depth-First Search,DFS)是算法竞赛和面试中最高频的暴力搜索算法之一。其核心思想是“一条路走到黑”,从起点出发,优先探索最深的节点,直到无…...
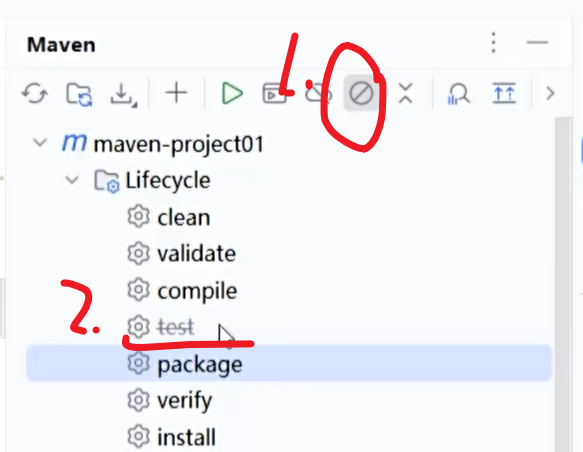
maven快速上手
之前我们项目如果要用到其他额外的jar包,需要自己去官网下载并且导入。但是有maven后,直接在maven的pom.xml文件里用代码配置即可,配置好后maven会自动帮我们联网下载并且会自动导入该jar包 在右边的maven中,我们可以看到下载安装…...

cplex12.9 安装教程以及下载
cplex 感觉不是很好找,尤其是教育版,我这里提供一个版本,在下面的图可以看到,不仅可以配置matlab,也可以配置vs,现在拿vs2017来测试一下,具体文件的文件有需要的可以复制下面的链接获取 我用网盘分享了「c…...

甘特图实例 dhtmlxGantt.js
本文介绍了如何使用dhtmlxGantt库创建一个基础的甘特图示例,并对其进行汉化和自定义配置。首先,通过引入dhtmlxgantt.css和dhtmlxgantt.js文件初始化甘特图。接着,通过设置gantt.i18n.setLocale("cn")实现核心文本的汉化࿰…...

AMD硬件笔试面试题型解析
本专栏预计更新60期左右。当前第12期 这个系列通过在各类网上搜索大厂公开的笔试和面试题目,然后构造相关的知识点矩阵,让大家对核心的知识点有更深的认识,这个过程虽然耗时费力,但大厂的很多题目确实非常巧妙,很有代表性。由于官方没有发布过这样的题库,所以文章中的题目…...

视频剪辑 VEGAS - 配置视频片段保持原长宽比
VEGAS 配置视频片段保持原长宽比 右击视频片段 -> 选择【开关】 -> 勾选【保持长宽比】 右击视频片段 -> 点击【属性】 -> 弹出【属性】窗口 点击【媒体】 -> 选择【像素宽高比】为【1,0000(方形)】...

力扣 54 .螺旋矩阵
文章目录 题目介绍题解 题目介绍 题解 代码如下: class Solution {public List<Integer> spiralOrder(int[][] matrix) {List<Integer> res new ArrayList<>();if (matrix.length 0){return res;}int l 0, r matrix[0].length - 1, t 0, b…...

四、【API 开发篇 (上)】:使用 Django REST Framework 构建项目与模块 CRUD API
【API 开发篇 】:使用 Django REST Framework 构建项目与模块 CRUD API 前言为什么选择 Django REST Framework (DRF)?第一步:创建 Serializers (序列化器)第二步:创建 ViewSets (视图集)第三步:配置 URLs (路由)第四步…...

python使用pycharm和conda 设置默认使用清华镜像
将步骤分为Conda配置和PyCharm配置两部分。Conda部分包括添加镜像源、调整优先级、更新环境。PyCharm部分需要根据版本说明如何添加镜像源到项目解释器设置中。同时,需要验证配置是否成功,并提醒常见问题,比如路径错误或缓存问题。需要确保引…...

Prometheus+Grafana实现对服务的监控
PrometheusGrafana实现对服务的监控 前言:PrometheusGrafana实现监控会更加全面,监控的组件更多 Prometheus官网 https://prometheus.io/docs/prometheus/latest/getting_started/ Grafana官网 https://grafana.com/docs/ 一、安装PrometheusGrafana 这…...

ARM笔记-ARM伪指令及编程基础
第四章 ARM伪指令及编程基础 4.1 伪指令概述 4.1.1 伪指令定义 人们设计了一些专门用于指导汇编器进行汇编工作的指令,由于这些指令不形成机器码指令,它们只是在汇编器进行汇编工作的过程中起作用,所以被叫做伪指令。 4.1.2 伪指令特征 …...

Python入门手册:Python基础语法
Python是一种简洁、易读且功能强大的编程语言,非常适合初学者入门。无论你是编程新手,还是有一定编程基础但想学习Python的开发者,掌握Python的基础语法都是迈向高效编程的第一步。本文将详细介绍Python的基本语法,包括变量和数据…...

SpringBoot-SpringBoot源码解读
SpringBoot-SpringBoot源码解读 一、Spring Boot启动过程概述 Spring Boot通过一系列的类和机制,简化了Spring应用的启动流程。当你执行SpringApplication.run()时,Spring Boot会自动完成应用的初始化、环境配置、组件加载、自动配置等任务,…...
CAD如何导出PDF?PDF如何转CAD?详细教程来了
浩辰CAD看图王是一款功能强大的CAD图纸查看与编辑工具,其核心功能之一便是支持CAD与PDF格式的互转。下面是CAD看图王输出PDF和PDF转CAD功能的详细介绍及操作步骤: 一、输出PDF功能 看图王可以将CAD图纸转换为PDF格式,是文件在不同的设备上显…...

python-数据可视化(大数据、数据分析、可视化图像、HTML页面)
通过 Python 读取 XLS 、CSV文件中的数据,对数据进行处理,然后生成包含柱状图、扇形图和折线图的 HTML 报告。这个方案使用了 pandas 处理数据,matplotlib 生成图表,并将图表嵌入到 HTML 页面中。 1.XSL文件生成可视化图像、生成h…...

el-select中自定义 两组el-option,但是key不一样,并且点击需获取当前整个项的所有属性
当el-select中只有一组el-option , 获取点击的当前项的属性 , el-select 绑定:value-keyid 但是 当el-select中有两组el-option ,每组option的key不一致,如下代码所示 <el-selectv-model"sth" change"choosee":value-key"…...
【笔记】OpenCV的学习(未完)
由于只记关键和不懂的部分 希望做到下次再看这部分笔记就记得 所以用词会非常简练 前向传播 输入数据依次经过模型的各层,按照各层定义的运算规则进行计算,最终得到模型预测输出的过程。 单向的信息流动,不涉及模型参数的更新。 助于思考的…...

多模态大语言模型arxiv论文略读(八十七)
MG-LLaVA: Towards Multi-Granularity Visual Instruction Tuning ➡️ 论文标题:MG-LLaVA: Towards Multi-Granularity Visual Instruction Tuning ➡️ 论文作者:Xiangyu Zhao, Xiangtai Li, Haodong Duan, Haian Huang, Yining Li, Kai Chen, Hua Ya…...

《棒球百科》长寿运动排名·棒球1号位
关于长寿运动的排名,运动长寿秘诀: 一、全球公认的「长寿运动」排名 游泳(低冲击、强化心肺) 快走/健走(每日30分钟降低15%早逝风险) 太极拳(平衡力减压,哈佛研究称可延缓衰老&am…...
