leetcode105.从中序与前序遍历序列构造二叉树:前序定根与中序分治的递归重建术
一、题目深度解析与核心挑战
在二叉树的重建问题中,"从中序与前序遍历序列构造二叉树"是一道考察递归分治思想的经典题目。题目要求我们根据一棵二叉树的前序遍历序列和中序遍历序列,重建出该二叉树的原始结构。这道题的核心难点在于如何利用两种遍历序列的特性,高效定位子树的根节点,并通过递归分治策略构建完整的树结构。
遍历序列特性回顾:
- 前序遍历(Preorder):根-左-右,第一个元素是当前子树的根节点
- 中序遍历(Inorder):左-根-右,根节点将序列分为左子树和右子树两部分
示例输入输出:
输入:
前序 preorder = [3,9,20,15,7]
中序 inorder = [9,3,15,20,7]
输出:
3/ \9 20/ \15 7
重建的核心逻辑在于:每次通过前序的第一个元素确定根节点,再通过中序中根节点的位置分割出左右子树的范围,递归构建子树。
二、递归解法的核心实现与数据结构设计
完整递归代码实现
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {Map<Integer, Integer> map; // 存储中序值到索引的映射public TreeNode buildTree(int[] preorder, int[] inorder) {map = new HashMap<>();for (int i = 0; i < inorder.length; i++) {map.put(inorder[i], i); // 预处理中序索引,O(n)时间}return findTree(preorder, 0, preorder.length, inorder, 0, inorder.length);}public TreeNode findTree(int[] preorder, int preBegin, int preEnd, int[] inorder, int inBegin, int inEnd) {if (preBegin >= preEnd || inBegin >= inEnd) {return null; // 子数组为空,返回null}// 前序第一个元素是当前子树的根节点int rootVal = preorder[preBegin]; int rootIndex = map.get(rootVal); // 中序中根节点的索引TreeNode root = new TreeNode(rootVal); // 创建根节点// 计算左子树长度:中序中根节点左边的元素个数int lenLeft = rootIndex - inBegin; // 递归构建左子树:前序[preBegin+1, preBegin+lenLeft+1),中序[inBegin, rootIndex)root.left = findTree(preorder, preBegin + 1, preBegin + lenLeft + 1, inorder, inBegin, rootIndex);// 递归构建右子树:前序[preBegin+lenLeft+1, preEnd),中序[rootIndex+1, inEnd)root.right = findTree(preorder, preBegin + lenLeft + 1, preEnd, inorder, rootIndex + 1, inEnd);return root;}
}
核心数据结构设计:
-
HashMap映射表:
- 作用:快速查找中序遍历中值对应的索引(O(1)时间复杂度)
- 预处理:遍历中序数组,将每个值与其索引存入map
- 关键价值:避免每次查找根节点索引时遍历中序数组,将时间复杂度从O(n²)优化到O(n log n)
-
递归函数参数:
preBegin/preEnd:前序数组当前处理的子数组范围(左闭右开)inBegin/inEnd:中序数组当前处理的子数组范围(左闭右开)- 意义:通过索引范围精确划分当前子树的左右子树区域,避免数据拷贝
三、核心问题解析:索引定位与递归分治过程
1. 根节点定位的核心逻辑
前序遍历的根节点特性
int rootVal = preorder[preBegin]; // 前序第一个元素是根节点
int rootIndex = map.get(rootVal); // 中序中根节点的位置
- 前序特性:前序遍历的第一个元素必定是当前子树的根节点(先访问根节点,再访问左右子树)
- 中序分割:根节点在中序中的位置将序列分为左子树(左边元素)和右子树(右边元素)
示例说明:
- 前序数组
[3,9,20,15,7]的第一个元素是3,确定根节点为3 - 中序数组
[9,3,15,20,7]中3的索引是1,左边是左子树[9],右边是右子树[15,20,7]
2. 左右子树的索引划分
左子树范围确定
int lenLeft = rootIndex - inBegin; // 左子树元素个数
// 前序左子树范围:preBegin+1 到 preBegin+lenLeft+1
root.left = findTree(preorder, preBegin + 1, preBegin + lenLeft + 1, inorder, inBegin, rootIndex);
- 中序左子树:从
inBegin到rootIndex(左闭右开,包含根节点左边的所有元素) - 前序左子树:前序中左子树的元素个数与中序左子树相同,起始索引为
preBegin+1(跳过根节点),结束索引为preBegin+lenLeft+1
右子树范围确定
// 中序右子树:从rootIndex+1到inEnd
// 前序右子树:左子树之后到preEnd(左子树结束索引为preBegin+lenLeft+1)
root.right = findTree(preorder, preBegin + lenLeft + 1, preEnd, inorder, rootIndex + 1, inEnd);
- 关键公式:前序中右子树的起始索引 = 左子树结束索引(preBegin+lenLeft+1)
- 逻辑推导:前序中根节点后,先排列左子树所有元素,再排列右子树所有元素,因此右子树的起始位置是左子树结束之后
3. 递归终止条件
if (preBegin >= preEnd || inBegin >= inEnd) {return null;
}
- 触发场景:当子数组长度为0(preBegin == preEnd或inBegin == inEnd)
- 逻辑意义:表示当前子树不存在,返回null作为叶子节点的子节点,确保递归正确终止
四、递归分治流程模拟:以示例输入为例
示例输入:
- 前序:
[3,9,20,15,7](索引0-4) - 中序:
[9,3,15,20,7](索引0-4)
详细递归过程:
-
第一次调用(构建整棵树):
- preBegin=0, preEnd=5;inBegin=0, inEnd=5
- 根节点:preorder[0]=3,中序索引1
- 左子树长度:1-0=1(元素9)
- 右子树长度:5-1-1=3(元素15,20,7)
-
构建左子树:
- 前序范围[1,2](元素9),中序范围[0,1](元素9)
- 根节点:preorder[1]=9,中序索引0
- 左右子树长度均为0,递归终止,左子树为叶子节点9
-
构建右子树:
- 前序范围[2,5](元素20,15,7),中序范围[2,5](元素15,20,7)
- 根节点:preorder[2]=20,中序索引3
- 左子树长度:3-2=1(元素15),右子树长度:5-3-1=1(元素7)
-
右子树的左子树(15):
- 前序范围[3,4](元素15),中序范围[2,3](元素15)
- 根节点:preorder[3]=15,中序索引2,左右子树为空,构建叶子节点15
-
右子树的右子树(7):
- 前序范围[4,5](元素7),中序范围[4,5](元素7)
- 根节点:preorder[4]=7,中序索引4,左右子树为空,构建叶子节点7
最终构建的树结构:
3/ \9 20/ \15 7
五、算法复杂度分析
1. 时间复杂度
- O(n):每个节点仅被创建一次,HashMap预处理O(n),每次递归分割子数组O(1)
- 分治策略下,每个层级的总操作数为O(n),总共有O(log n)层(平衡树),最坏O(n)层(链表树),总体仍为O(n)
2. 空间复杂度
- O(n):HashMap存储n个元素,递归栈深度O(n)(最坏情况树退化为链表)
3. 核心优化点
- HashMap索引预处理:将中序索引查找从O(n)优化到O(1),避免双重循环
- 分治策略:通过索引范围划分,每次递归将问题规模减半,符合分治思想
- 无数据拷贝:通过索引范围传递,避免复制子数组,节省空间
六、核心技术点总结:前序中序重建的三大关键步骤
1. 根节点的唯一性定位
- 前序特性:第一个元素是根节点,确保每次递归有且仅有一个根节点
- 中序分割:根节点在中序中的位置将序列分为左右子树,保证子问题独立性
- 时间优化:HashMap实现O(1)时间的根节点定位
2. 子树范围的数学推导
- 左子树长度:
rootIndex - inBegin(中序左边元素个数) - 前序左子树范围:起始索引=preBegin+1,结束索引=preBegin+lenLeft+1
- 解释:preBegin是根节点索引,+1跳过根节点,+lenLeft是左子树元素个数,+1是因为左闭右开
- 前序右子树范围:起始索引=左子树结束索引,结束索引=preEnd
3. 递归终止的边界处理
- 空数组判断:当子数组长度为0时返回null,作为递归终止条件
- 正确性保证:每个子树的左右边界通过索引严格控制,避免越界访问
- 逻辑闭环:递归终止时返回null,确保叶子节点的子节点正确设置
七、常见误区与边界情况处理
1. 空树处理
- 输入为空数组时,
preBegin >= preEnd自动触发,返回null,无需额外处理
2. 单节点树
- 前序和中序均只有一个元素,直接创建节点,递归终止条件正确处理
- 示例:preorder=[1], inorder=[1],直接返回节点1
3. 完全左/右子树
- 例如前序
[1,2,3],中序[1,2,3],根节点是1,左子树为空,右子树递归构建2和3 - 关键:正确计算lenLeft=0,前序右子树范围为preBegin+0+1=1到preEnd=3,即元素2和3
八、总结:递归分治在树重建中的设计哲学
本算法通过"前序定根-中序分治-递归构建"的三步策略,完美解决了从中序与前序序列重建二叉树的问题。其核心设计哲学包括:
-
特性利用:
- 前序遍历的根节点特性(第一个元素)
- 中序遍历的左右子树划分特性
-
索引魔法:
- 通过HashMap实现中序值到索引的快速查找
- 利用数学推导确定前序中左右子树的索引范围,实现O(1)时间的子数组划分
-
递归分治:
- 将原问题分解为左右子树的重建子问题
- 通过索引范围传递,避免数据拷贝,实现线性时间复杂度
这种解法不仅高效,而且逻辑清晰,充分体现了递归分治在树结构问题中的优势。理解索引定位的数学推导和递归边界的处理,是掌握此类问题的关键。在实际应用中,这种分治思想还可迁移到后序与中序重建、不同遍历序列的树重建等问题中,具有很强的通用性。
通过前序和中序重建二叉树的核心,在于利用两种遍历序列的特性,将树的重建问题转化为子树的递归重建问题,而索引的正确划分则是实现这一转化的关键桥梁。
相关文章:

leetcode105.从中序与前序遍历序列构造二叉树:前序定根与中序分治的递归重建术
一、题目深度解析与核心挑战 在二叉树的重建问题中,"从中序与前序遍历序列构造二叉树"是一道考察递归分治思想的经典题目。题目要求我们根据一棵二叉树的前序遍历序列和中序遍历序列,重建出该二叉树的原始结构。这道题的核心难点在于如何利用…...

Python二级考试
目录 一、核心知识模块 1. 程序结构 2. 循环结构 3. 组合数据类型 4. 函数与模块 二、重点算法 1. 排序算法 2. 查找算法 三、文件操作 1. 基础文件处理 四、备考建议 五、典型易错点 以下是Python二级考试的复习要点整理,分为知识模块和备考建议&#…...

DeepSeek联网Google搜索引擎
目录: 1、使用背景2、实现代码3、Gradio 的 yield 机制 1、使用背景 比如所有易建联是什么时候退役的?使用大模型对这种实事回答不准确,需要通过联网搜索处理。 正确答案应该是2023年8月29日退役。 2、实现代码 # import gradio as gr# d…...
时,经典理论失效?)
理论物理:为什么在极低温(接近绝对零度)时,经典理论失效?
经典理论应该是指经典力学和经典统计物理吧,比如牛顿力学、麦克斯韦-玻尔兹曼分布这些。而到了接近绝对零度的时候,物质的状态会发生什么变化呢?比如说超流性、超导性,或者玻色-爱因斯坦凝聚这些现象,这些在经典理论里好像没法解释。 因为在极低温下,粒子的热运动减弱,…...

奈雪小程序任务脚本
功能概述 该脚本用于自动完成奈雪点单小程序的每日任务,包括: 自动检测 Token 有效性自动签到(如果未签到)获取用户基础信息(昵称、手机号)查询当前奈雪币余额记录连续签到天数支持多账号执行,…...

上海医日健集团物联网专利技术领跑智慧药房赛道
在智慧医疗蓬勃发展的浪潮中,上海医日健集团凭借其卓越的创新能力与强大的技术实力,在智慧药房领域崭露头角。集团自主研发的物联网专利技术,正以前所未有的优势,重塑智慧药房运营模式,引领行业迈向新的发展高度。 上…...

基于Java+MySQL实现(Web)图书借阅管理系统
图书借阅管理系统(前后台) 1 需求分析 图书借阅管理系统是模拟学校图书馆实现的一个具有前后台的 Web 系统.对于读者,能够提供全文检索,个性化推荐,借阅等功能.对于管理员,能够提供可视化数据分析,信息管理等功能. 2 技术栈 前端: Layui,jQuery,echarts 后端:Spring Boot,…...

SAR ADC的功耗设计
SAR ADC 由比较器、逻辑和DAC组成,功耗比可能是3:6:1,对于低功耗设计来说,我们需要尽量让DAC的功耗最小,这里来探讨一下CDAC的功耗计算方法。 CDAC从状态1切换到状态2时,需要从Vref buffer上抽拉电荷。C是状态2时连接Vref的总电容,V2就是状态2时接Vref的电容上的电压…...

PP-OCRv5
目录 PP-OCRv5官方效果如下 C封装、C#调用效果 项目 代码 下载 PP-OCRv5官方效果如下 C封装、C#调用效果 项目 代码 using Newtonsoft.Json; using OpenCvSharp; using System; using System.Collections.Generic; using System.Diagnostics; using System.Drawing; usi…...
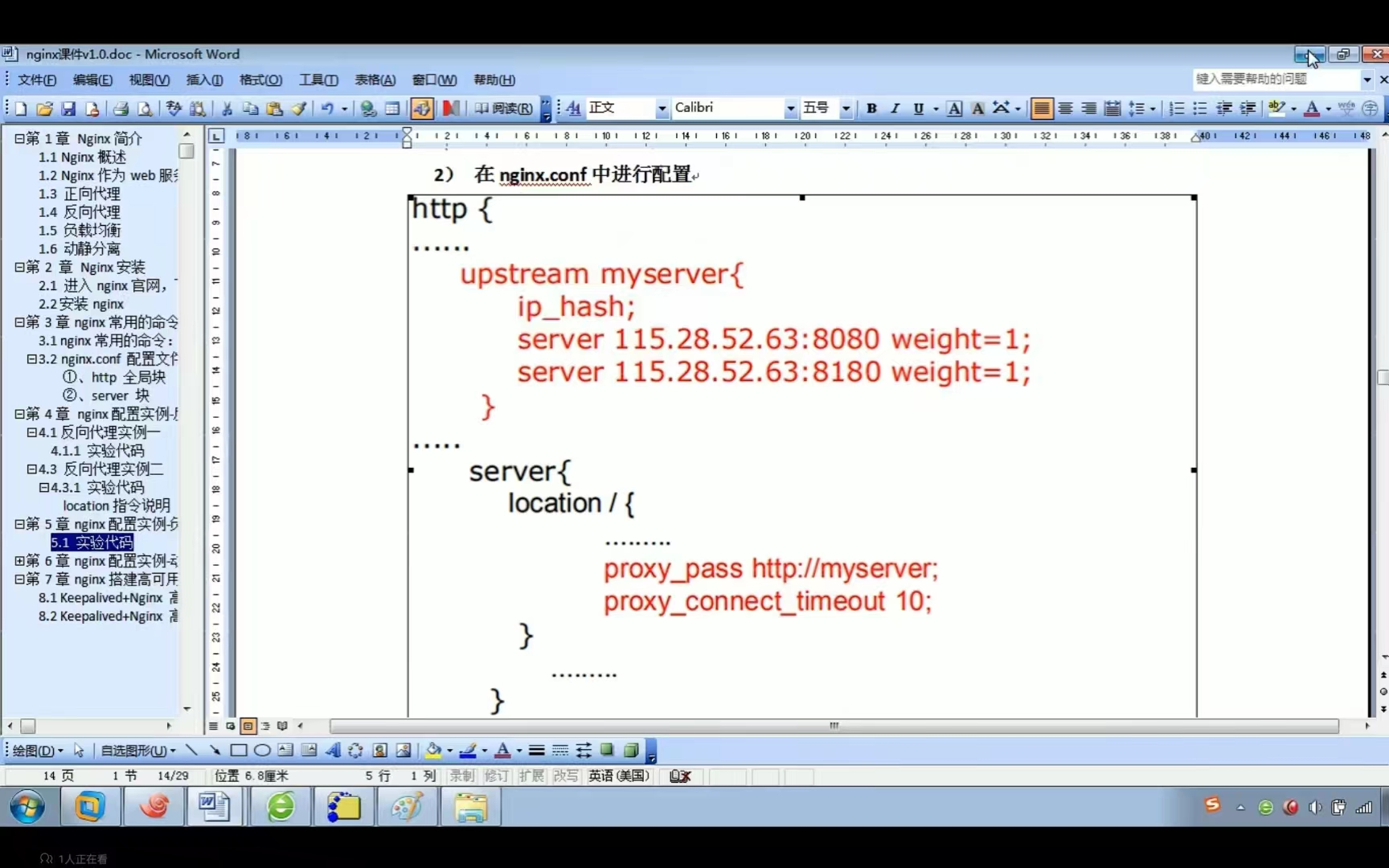
nginx的一些配置的意思
1.用这个端口可以访问到nginx 2.工作进程,设置成和cpu核心数一样即可 3.每个工作进程的最大网络连接数。 4.主机名称 设置反向代理时,把server_name设置成ip。 5.反向代理进行转发,localhost指的是nginx所在的机器。 关键字proxy_pass。 …...

Agent模型微调
这篇文章讲解: 把 Agent 和 Fine-Tuning 的知识串起来,在更高的技术视角看大模型应用;加深对 Agent 工作原理的理解;加深对 Fine-Tuning 训练数据处理的理解。 1. 认识大模型 Agent 1.1 大模型 Agent 的应用场景 揭秘Agent核心…...

Android-OkHttp与Retrofit学习总结
OkHttp核心机制与工作流程 面试官:能简单介绍一下OkHttp的工作流程吗? 候选人: 好的,OkHttp的工作流程大致可以分为几个步骤。首先,我们需要创建一个OkHttpClient实例,通常会用建造者模式来配置…...

移远三款主流5G模块RM500U,RM520N,RG200U比较
文章目录 概要一、技术架构差异1. 3GPP协议版本2. 芯片平台与性能3. 频段覆盖与区域适配4. 协议增强与特殊功能 二、功能与应用定位1. 网络兼容性2. 封装与接口扩展 三、典型应用场景总结 概要 本文介绍下移远两款主流5G模块RM500U RM520N RG200U。 一…...

C++引用以及和指针的区别
C++ 引用 引用(reference)是 C++ 中的一种变量类型,是另一个变量的别名。一旦引用被初始化,就不能再改变它所指向的对象。 引用的特点 必须初始化:声明引用时必须立即对其进行初始化。不可更改绑定:一旦引用绑定到某个变量,就不能再指向其他变量。语法简洁:使用引用不…...

firfox 国外版和国内版本账号不互通问题处理
https://blog.csdn.net/sinat_37891718/article/details/147445621 现在国际服的火狐浏览器修改使用国内的账号服务器,需要先在搜索框输入about:config 中改变三项配置,然后重启浏览器,才能正常使用国内的火狐账号服务器 identity.fxaccount…...

Linux基本指令篇 —— whoami指令
whoami 是 Linux 和 Unix 系统中一个简单但实用的命令,全称 Who Am I(我是谁)。它的功能是显示当前登录用户的用户名。以下是关于 whoami 的详细解析: 目录 1. 基本用法 2. 命令特点 3. 实际应用场景 场景 1:脚本中…...
--异步调用+多路复用实现)
用go从零构建写一个RPC(3)--异步调用+多路复用实现
在前两个版本中,我们实现了基础的客户端-服务端通信、连接池、序列化等关键模块。为了进一步提升吞吐量和并发性能,本版本新增了 异步发送机制 和 多路复用支持,旨在减少资源消耗、提升连接利用率。 代码地址:https://github.com/…...

力扣395做题笔记
题目链接 力扣395 第一次尝试 class Solution {public int longestSubstring(String str, int k) {char[] s str.toCharArray();int n s.length;int[] cnts new int[256];int ans 0;for (int r 0, l 0; r < n; r ) { cnts[s[r]];if (cnts[s[r]] > k) { ans Mat…...

Python-numpy中常用的统计函数及转换函数
numpy中常用的统计函数 numpy中常用统计函数numpy普通统计函数忽略 NaN 值进行统计百分位数 numpy中形状转换函数重塑数组(reshape)展平数组(flatten/ravel)转置(transpose/T) 数据类型的转换使用astype()转…...

【C语言干货】free细节
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、为啥*phead free掉了之后,为啥下面还 提示:以下是本篇文章正文内容,下面案例可供 可以用? 前言参考 一、为…...
 2-0 等级保护制度现行技术标准)
网络安全-等级保护(等保) 2-0 等级保护制度现行技术标准
################################################################################ 第二章:现行等保标准要求,通过表格方式详细拆分了等保的相关要求。 GB 17859-1999 计算机信息系统 安全保护等级划分准则【现行】 GB/T22240-2020 《信息安全技术 网…...

WebSocket(看这一篇就够了)
文章目录 WebSocket 基本概念什么是WebSocket?为什么需要 WebSocket?与 HTTP 协议的区别WebSocket协议的原理WebSocket工作流程WebSocket 数据帧结构和控制帧结构。JavaScript 中 WebSocket 对象的属性和方法,以及如何创建和连接 WebSocket。webSocket简…...
旧物回收小程序:让闲置焕发光彩,为生活增添价值
你是否常常为家中堆积如山的闲置物品而烦恼?那些曾经心爱的物品,如今却成了占据空间的“鸡肋”,丢弃可惜,留着又无处安放。别担心,一款旧物二手回收小程序将为你解决这一难题,让闲置物品重新焕发光彩&#…...
:黏性阶段的功能优先级法则——七问决策模型与风险控制)
精益数据分析(73/126):黏性阶段的功能优先级法则——七问决策模型与风险控制
精益数据分析(73/126):黏性阶段的功能优先级法则——七问决策模型与风险控制 在创业的黏性阶段,如何从海量的功能创意中筛选出真正能提升用户留存的关键改动?今天,我们结合《精益数据分析》中的“开发功能…...
与Vue响应式系统(自动优化,中小型项目,快速开发)区别)
React声明式编程(手动控制,大型项目,深度定制)与Vue响应式系统(自动优化,中小型项目,快速开发)区别
文章目录 React声明式与Vue响应式区别详解一、响应式机制原理对比1.1 Vue的响应式系统Vue响应式流程图Vue响应式代码示例 1.2 React的声明式更新React声明式流程图React声明式代码示例 二、更新触发逻辑差异2.1 Vue的自动更新Vue依赖收集机制 2.2 React的手动更新React Diff算法…...

数学建模MathAI智能体-2025电工杯A题实战
题目: 光伏电站发电功率日前预测问题 光伏发电是通过半导体材料的光电效应,将太阳能直接转化为电能的技术。光伏电站是由众多光伏发电单元组成的规模化发电设施。 光伏电站的发电功率主要由光伏板表面接收到的太阳辐射总量决定,不同季节太阳…...

跨平台游戏引擎 Axmol-2.6.0 发布
Axmol 2.6.0 版本是一个以错误修复和功能改进为主的次要LTS长期支持版本 🙏感谢所有贡献者及财务赞助者:scorewarrior、peterkharitonov、duong、thienphuoc、bingsoo、asnagni、paulocoutinhox、DelinWorks 相对于2.5.0版本的重要变更: 通…...

C# Windows Forms应用程序-002
目录 项目结构 主类和命名空间 构造函数和析构函数 初始化组件 (InitializeComponent) 按钮点击事件处理程序 主程序入口点 项目截图: 完整代码: 项目结构 这个项目是一个简单的C# Windows Forms应用程序,获取指定文件的根信息…...

理解计算机系统_线程(八):并行
前言 以<深入理解计算机系统>(以下称“本书”)内容为基础,对程序的整个过程进行梳理。本书内容对整个计算机系统做了系统性导引,每部分内容都是单独的一门课.学习深度根据自己需要来定 引入 接续理解计算机系统_并发编程(10)_线程(七):基于预线程化的…...

【MySQL】09.索引
索引是用来提高数据库的性能的,但查询速度的提高是以插入、更新、删除的速度为代价的,这些写操作,增加了大量的IO。所以它的价值在于提高一个海量数据的检索速度。 1. 认识磁盘 MySQL 给用户提供存储服务,而存储的都是数据&…...
