【R语言编程绘图-函数篇】
基础函数绘制
R语言可通过curve()函数直接绘制数学函数图形,无需预先生成数据点。例如绘制正弦函数:
curve(sin, from = -pi, to = pi, col = "blue", lwd = 2)
自定义函数绘制
对于用户自定义函数,需先定义函数表达式:
my_function <- function(x) x^2 + 2*x + 1
curve(my_function, from = -5, to 5, n = 1000)
多函数叠加绘制
使用add = TRUE参数可在同一图形上叠加多个函数:
curve(sin, -pi, pi, col = "red")
curve(cos, -pi, pi, col = "blue", add = TRUE)
参数化函数绘制
处理含参数的函数时,可通过匿名函数传递参数:
a <- 2
curve(function(x) a*sin(x), 0, 2*pi)
离散点绘制法
对于无法用表达式表示的函数,可生成离散点后绘图:
x <- seq(-3, 3, length.out = 100)
y <- dnorm(x) # 标准正态分布密度函数
plot(x, y, type = "l")
图形定制技巧
通过图形参数增强可视化效果:
curve(exp, -2, 2, main = "Exponential Function",xlab = "Input", ylab = "Output",col = "darkgreen", lty = 2)
grid() # 添加网格线
特殊函数绘制
统计分布函数可直接调用:
curve(dnorm, -3, 3) # 正态分布密度
curve(pnorm, -3, 3) # 正态分布累积概率



# 设置随机种子
set.seed(123)# 定义x值范围
x <- seq(-10, 10, length.out = 200)# 设置图形布局为3行4列
par(mfrow = c(2, 2), mar = c(4, 4, 2, 2)) # 调整边距# 1. 线性函数
y1 <- 2 + 0.5 * x
plot(x, y1, type = "l", col = "blue", lwd = 2, main = "Linear Function", xlab = "x", ylab = "y")# 2. 多项式函数
y2 <- 2 + 0.5 * x + 0.1 * x^2
plot(x, y2, type = "l", col = "red", lwd = 2, main = "Polynomial Function", xlab = "x", ylab = "y")# 3. 指数函数
y3 <- 2 * exp(0.3 * x)
plot(x, y3, type = "l", col = "green", lwd = 2, main = "Exponential Function", xlab = "x", ylab = "y")# 4. 对数函数
y4 <- 2 + 0.5 * log(abs(x) + 1) # 避免对负数取对数
plot(x, y4, type = "l", col = "purple", lwd = 2, main = "Logarithmic Function", xlab = "x", ylab = "y")# 设置图形布局为3行4列
par(mfrow = c(2, 2), mar = c(4, 4, 2, 2)) # 调整边距# 5. 幂函数
y5 <- 2 * x^0.5
plot(x, y5, type = "l", col = "orange", lwd = 2, main = "Power Function", xlab = "x", ylab = "y")# 6. 逻辑函数
y6 <- 1 / (1 + exp(-(2 + 0.5 * x)))
plot(x, y6, type = "l", col = "brown", lwd = 2, main = "Logistic Function", xlab = "x", ylab = "y")# 7. 正弦函数
y7 <- 2 * sin(0.5 * x + 1)
plot(x, y7, type = "l", col = "pink", lwd = 2, main = "Sine Function", xlab = "x", ylab = "y")# 8. 余弦函数
y8 <- 2 * cos(0.5 * x + 1)
plot(x, y8, type = "l", col = "cyan", lwd = 2, main = "Cosine Function", xlab = "x", ylab = "y")# 设置图形布局为3行4列
par(mfrow = c(2, 2), mar = c(4, 4, 2, 2)) # 调整边距# 9. 高斯函数
y9 <- 2 * exp(-((x - 0)^2) / (2 * 1^2))
plot(x, y9, type = "l", col = "magenta", lwd = 2, main = "Gaussian Function", xlab = "x", ylab = "y")# 10. 双曲函数
y10 <- 2 * tanh(0.5 * x + 1)
plot(x, y10, type = "l", col = "gray", lwd = 2, main = "Hyperbolic Function", xlab = "x", ylab = "y")# 11. 双指数函数y11 <- 2 * exp(-0.5 * abs(x))
plot(x, y11, type = "l", col = "gray", lwd = 2, main = "Hyperbolic Function", xlab = "x", ylab = "y")# 12. 三次多项式函数y12 <- 2 + 0.5 * x + 0.1 * x^2 + 0.01 * x^3
plot(x, y12, type = "l", col = "gray", lwd = 2, main = "Hyperbolic Function", xlab = "x", ylab = "y")相关文章:

【R语言编程绘图-函数篇】
基础函数绘制 R语言可通过curve()函数直接绘制数学函数图形,无需预先生成数据点。例如绘制正弦函数: curve(sin, from -pi, to pi, col "blue", lwd 2)自定义函数绘制 对于用户自定义函数,需先定义函数表达式: …...

训练自己的yolo模型,并部署到rk3588上
文章目录 1. 训练自己的模型2. pt转onnx3. onnx转rknn4. 后续…… 1. 训练自己的模型 如何训练自己的yolo模型,网络上已经有足够多的教程,这里只简单的描述一下。如果已经有了自己的.pt模型,那么可以直接跳转到第二节。 此处是以检测模型的…...

Leetcode 3556. Sum of Largest Prime Substrings
Leetcode 3556. Sum of Largest Prime Substrings 1. 解题思路2. 代码实现3. 算法优化 题目链接:3556. Sum of Largest Prime Substrings 1. 解题思路 这一题毕竟只是这一次双周赛的第一题,虽然标记为medium的题目,但是思路上还是非常简单…...

以少学习:通过无标签数据从大型语言模型进行知识蒸馏
Learning with Less: Knowledge Distillation from Large Language Models via Unlabeled Data 发表:NNACL-Findings 2025 机构:密歇根州立大学 Abstract 在实际的自然语言处理(NLP)应用中,大型语言模型(…...

鸿蒙OSUniApp 实现带有滑动删除的列表#三方框架 #Uniapp
使用 UniApp 实现带有滑动删除的列表 在移动应用开发中,滑动删除(Swipe to Delete)是一种常见且实用的交互方式,广泛应用于消息、待办、收藏等列表场景。用户只需在列表项上左右滑动,即可快速删除或管理数据。随着 Ha…...

Qt qml Network error问题
最近在学习Qt,需要调用地图,所以用到了QML,但是却遇到了这样的问题 d://qt_project//run//main.qml: Network error 现在我展示一下我的main文件的代码: #include <QApplication> #include <QQuickView> #include &l…...

Prompt工程:解锁大语言模型的终极密钥
Prompt工程:解锁大语言模型的终极密钥 一、引言:Prompt的战略价值重构 在人工智能技术加速渗透的2025年,Prompt(提示词)作为连接人类意图与大语言模型(LLM)的核心接口,其战略地位已…...
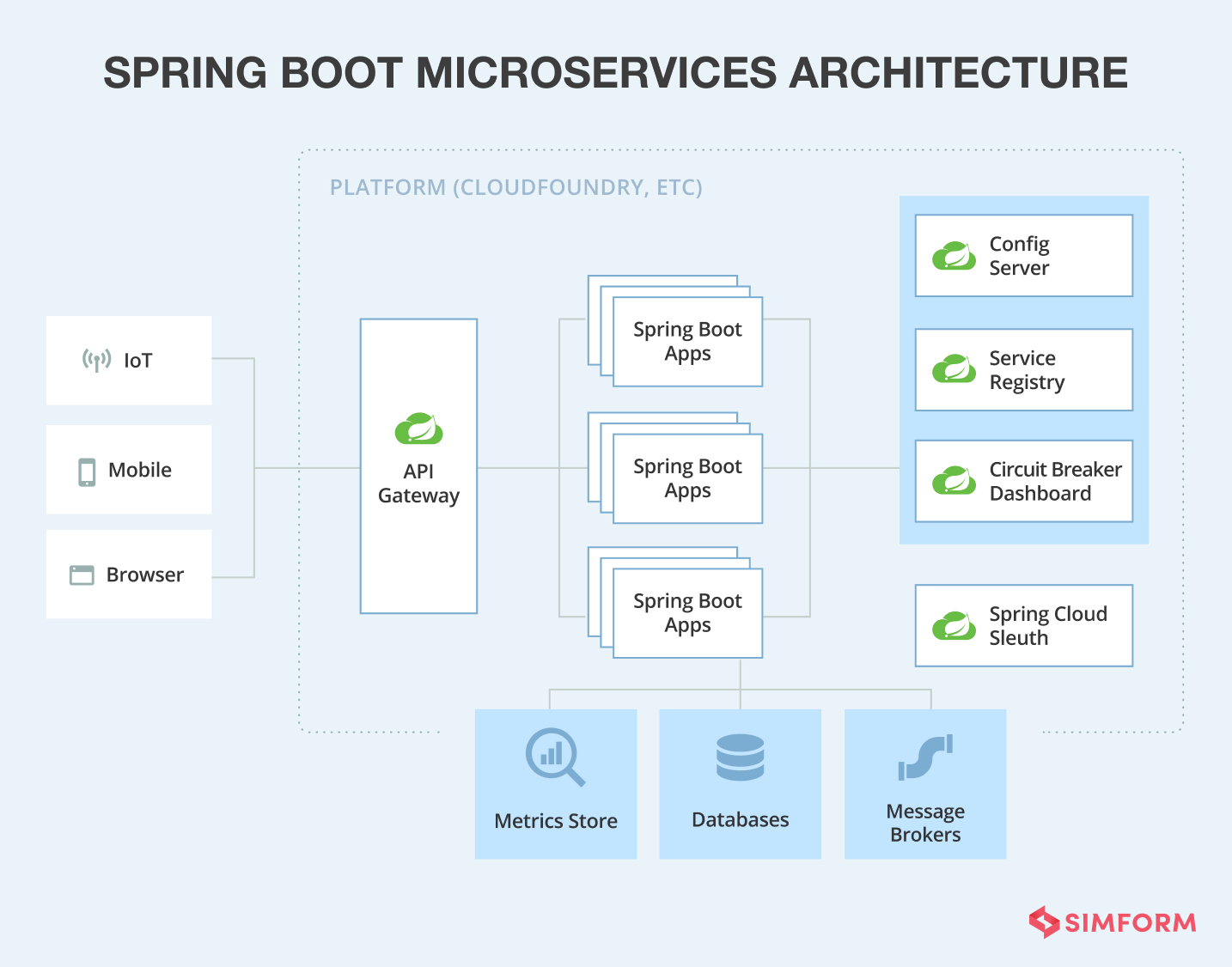
Spring Boot微服务架构(六):伪装的微服务有哪些问题?
伪装的微服务有哪些问题? 伪装的微服务架构(即表面上模仿微服务设计,但未真正遵循其核心原则的系统)通常具备以下特征点,这些特征可能导致系统复杂度增加、维护困难或性能下降: 1. 服务间强耦合 …...
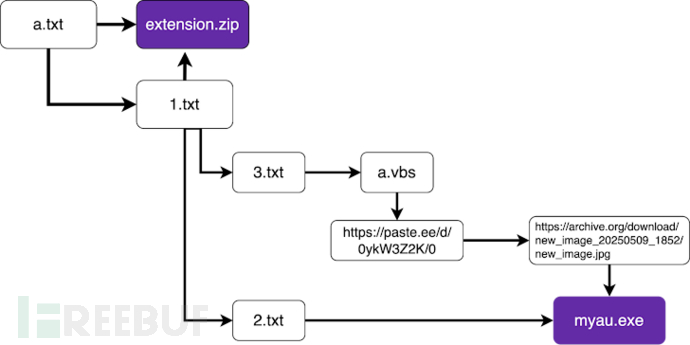
恶意npm与VS Code包窃取数据及加密货币资产
60个npm包窃取系统敏感信息 安全研究人员在npm软件包注册表中发现60个恶意组件,这些组件能够收集主机名、IP地址、DNS服务器和用户目录信息,并将其发送至Discord平台控制的终端节点。据Socket安全研究员Kirill Boychenko上周发布的报告显示,…...

Matlab快速上手五十六:详解符号运算里假设的用法,通过假设可以设置符号变量的取值范围,也可以通过假设设置变量属于集合:整数、正数和实数等
1.符号变量中假设的概念 在符号数学工具箱中,符号变量默认范围是全体复数,也就是说,符号运算是在全体复数域进行的,若需要运算中,不使用全体复数域,可以为变量设定取值范围,这就用到了假设&…...

机器学习笔记【Week1】
一、机器学习简介(Introduction) 什么是机器学习? 定义(Tom Mitchell): “A computer program is said to learn from experience E with respect to some task T and performance measure P, if its per…...

什么是3D全景视角?3D全景有什么魅力?
什么是3D全景视角?3D全景视角的全面解析。 3D全景视角,又称为3D全景技术或3D实景技术,是新兴的富媒体技术,基于静态图像和虚拟现实(VR)技术,通过全方位、无死角地捕捉和展示环境,为…...

【Mini-F5265-OB开发板试用测评】按键控制测试
本文介绍了如何使用按键控制 MCU 引脚的输出电平。 原理 由原理图可知 板载用户按键 K1 和 K2 分别与主控的 PB0 和 PB1 相连。 代码 #define _MAIN_C_#include "platform.h" #include "gpio_key_input.h" #include "main.h"int main(void) …...

Debian重装系统后
安装配置java环境 手动安装 下载openJDK:openJDK 设置替代项 sudo update-alternatives --install /usr/bin/java java /opt/jdk-21.0.2/bin/java 1 sudo update-alternatives --install /usr/bin/javac javac /opt/jdk-21.0.2/bin/javac 1 sudo update-alternat…...

每日Prompt:古花卷
提示词 主体对象 一本展开的古画卷 古画卷内呈现的内容 一片微型春秋鲁国,有古代马车,孔子乘坐周游列国,颜回、子路、子贡、曾参紧随其后 古画卷的外观状态 表面已经开裂和风化,呈现出年代感和历史感 与文字描述的首句一致&…...
)
[学习]C语言指针函数与函数指针详解(代码示例)
C语言指针函数与函数指针详解 文章目录 C语言指针函数与函数指针详解一、引言二、指针函数(函数返回指针)定义与语法典型应用场景注意事项 三、函数指针(指向函数的指针)定义与声明初始化与调用赋值方式调用语法 高级应用回调函数…...

夏季用电高峰如何防患于未“燃”?电力测温技术守护城市生命线
随着夏季来临用电负荷激增,电力系统面临严峻的高温考验,电力测温技术的重要性愈发凸显,电力安全是城市生命线工程的核心环节,电力测温已从"可选功能"升级为"必要的基础安全设施"。通过实时感知、智能分析和快…...
)
浙大版《Python 程序设计》题目集6-3,6-4,6-5,6-6列表或元组的数字元素求和及其变式(递归解法)
目录 6-3 输入格式: 输出格式: 输入样例: 输出样例: 6-4 输入格式: 输出格式: 输入样例: 输出样例: 6-5 输入格式: 输出格式: 输入样例: 输出样例: 6-6 输入格式: 输出格式: 输入样例: 输出样例: 6-3 第6章-3 列表或元组的数字元素求和 分数 20 全屏浏览 切换布局 作者 陈春晖 …...

Leetcode 3563. Lexicographically Smallest String After Adjacent Removals
Leetcode 3563. Lexicographically Smallest String After Adjacent Removals 1. 解题思路2. 代码实现 题目链接:3563. Lexicographically Smallest String After Adjacent Removals 1. 解题思路 这次的最后一题同样没有自力搞定,简直了…… 这道题还…...

【创造型模式】抽象工厂方法模式
文章目录 抽象工厂方法模式产品族与产品等级结构抽象工厂方法模式的角色和职责抽象工厂方法模式的实现抽象工厂方法模式的优缺点适用场景 抽象工厂方法模式 工厂方法模式引入了“工厂等级结构”,解决了简单工厂方法过分依赖单一工厂的问题。但是工厂方法模式存在的一…...

一台手机怎样实现多IP上网?方法有多种
在数字时代,多IP上网已成为许多手机用户的刚需。本文将详细介绍如何通过不同技术手段实现手机多IP上网,帮助读者根据实际需求选择适合的解决方案。 一、为什么一台手机要实现多IP上网 手机实现多IP上网的典型场景包括: ①防止同一IP操作多个…...
)
【FFmpeg+SDL】播放音频时,声音正常但是有杂音问题(已解决)
下面这个函数是SDL音频的回调函数(修改后的) void fill_audio(void *udata,Uint8 *stream,int len) {static int cc 0;cc;qDebug()<<QString::fromLocal8Bit("想要填充:%1字节").arg(len)<<cc;AudioOutput* is static_cast<AudioOutput*>(udat…...

Linux 527 重定向 2>1 rsync定时同步(未完)
rsync定时同步 配环境 关闭防火墙、selinux systemctl stop firewalld systemctl disable firewalld setenforce0 vim /etc/SELINUX/config SELINUXdisable515 设置主机名 systemctl set-hostname code systemctl set-hostname backup 配静态ip rsync 需要稳定的路由表和端…...

3DVR拍摄指南:从理论到实践
3DVR拍摄指南:从理论到实践 3D虚拟现实(Virtual Reality,简称VR)作为近年来迅速崛起的高新技术,通过电脑模拟产生一个三维空间的虚拟世界,为使用者提供视觉、听觉乃至触觉的全方位感官模拟,使用户仿佛身临…...

OSI模型中的网络协议
一、电子邮件协议:从SMTP到MIME的扩展 电子邮件系统的核心协议包括SMTP(Simple Mail Transfer Protocol)、POP3(Post Office Protocol)和IMAP(Internet Message Access Protocol),但…...

【C/C++】线程局部存储:原理与应用详解
文章目录 1 基础概念1.1 定义1.2 初始化规则1.3 全局TLS vs 局部静态TLS 2 内存布局2.1 实现机制2.2 典型内存结构2.3 性能特点 3 使用场景/用途3.1 场景3.2 用途 4 注意事项5 对比其他技术6 示例代码7 建议7.1 调试7.2 优化 8 学习资料9 总结 在 C 多线程编程中,线…...

分块查找详解
1、原理 分块查找(Block Search)是一种结合顺序查找与索引查找的算法,适用于数据分块存储且块内无序但块间有序的场景。它通过“分块-建立索引-逐层定位”提高查找效率。 分块查找的核心思想 数据分块 将数据集划分为若干块(子…...

leetcode hot100刷题日记——21.不同路径
和20题一样的思路link 题解: class Solution { public:int dfs(int i,int j,vector<vector<int>>&memo){//超过了边界,return 0if(i<0||j<0){return 0;}//从(0,0)到(0,0…...

Elasticsearch 如何实现跨数据中心的数据同步?
实战场景: 双数据中心容灾,要求RPO<5分钟,RTO<30分钟 RPO(Recovery Point Objective): RPO指的是灾难发生后,系统能够恢复到的数据更新点的时间。简单来说,它衡量的是数据…...

C语言学习笔记三 --- V
文章目录 程序入门设计 --- C 语言第二周 核心语法📝2.1 C 语言笔记 | 注释的使用(让代码会“说话”)💡 **注释的作用**🔍 **注释的两种写法**⚠️ **注释的注意事项**🔧 **注释的实用场景**📌 **本节总结**:📝 2.2 C 语言笔记 | 关键字(保留字)深度解析💡 …...
