代码随想录算法训练营 Day58 图论Ⅷ 拓扑排序 Dijkstra
图论
题目
117. 软件构建
拓扑排序:给出一个有向图,把这个有向图转成线性的排序就叫拓扑排序。
当然拓扑排序也要检测这个有向图是否有环,即存在循环依赖的情况,因为这种情况是不能做线性排序的。所以拓扑排序也是图论中判断有向无环图的常用方法。
本题使用 BFS 的拓扑排序思路

寻找出发边,特征是入度为0 出度为2,也就是没有边指向它,而它有两条边是指出去的。
接下来我给出拓扑排序的过程,其实就两步:
1. 找到入度为0 的节点,加入结果集
2. 将该节点从图中移除
循环以上两步,直到所有节点都在图中被移除了。
模拟过程



如果有环出现

这个图,我们只能将入度为0 的节点0 接入结果集。
之后,节点1、2、3、4 形成了环,找不到入度为0 的节点了,所以此时结果集里只有一个元素。
那么如果我们发现结果集元素个数不等于图中节点个数,我们就可以认定图中一定有有向环!
这也是拓扑排序判断有向环的方法。
#include <iostream>
#include <vector>
#include <queue>
#include <unordered_map>using namespace std;int main() {int m, n, s, t;cin >> n >> m;// 记录入度vector<int> inDegree(n, 0);// 使用邻接表记录图依赖关系unordered_map<int, vector<int>> umap;// 记录结果vector<int> res;for (int i = 0; i < m; ++i) {cin >> s >> t;inDegree[t]++;umap[s].push_back(t);}// 拓扑排序开始queue<int> que;// 寻找入度为0的元素加入队列for (int i = 0; i < n; ++i) {if (inDegree[i] == 0) que.push(i);}while (!que.empty()) {// 当前节点int cur = que.front();que.pop();res.push_back(cur);// 遍历节点指向for (int idx : umap[cur]) {inDegree[idx]--; // 通过 入度-- 实现图中删除这个节点if (inDegree[idx] == 0) que.push(idx);}}// 若不等于n说明有向图中有环if (res.size() == n) {for (int i = 0; i < n-1; ++i) {cout << res[i] << " ";}cout << res[n-1] << endl;}else cout << -1 << endl;
}
47. 参加科学大会(第六期模拟笔试)
最短路径 dijkstra 算法,求图中最短路径

思路
类似于 prim 算法,dijkstra 算法 同样是贪心的思路,不断寻找距离 源点最近的没有访问过的节点。
这里我也给出 dijkstra三部曲:
1. 第一步,选源点到哪个节点近且该节点未被访问过
2. 第二步,该最近节点被标记访问过
3. 第三步,更新非访问节点到源点的距离(即更新minDist数组)
在dijkstra算法中,同样有一个数组很重要,起名为:minDist。
minDist数组用来记录每一个节点距离源点的最小距离。
理解这一点很重要,也是理解 dijkstra 算法的核心所在。
朴素算法
初始化节点这里在强点一下 minDist数组的含义:记录所有节点到源点的最短路径,那么初始化的时候就应该初始为最大值,这样才能在后续出现最短路径的时候及时更新。

(图中,max 表示默认值,节点0 不做处理,统一从下标1 开始计算,这样下标和节点数值统一,方便大家理解,避免搞混)
源点(节点1) 到自己的距离为0,所以 minDist[1] = 0
此时所有节点都没有被访问过,所以 visited数组都为0
以下为dijkstra 三部曲
1、选源点到哪个节点近且该节点未被访问过,源点距离源点最近,距离为0,且未被访问。
2、该最近节点被标记访问过,标记源点访问过
3、更新非访问节点到源点的距离(即更新minDist数组) ,如图:

更新 minDist数组,即:源点(节点1) 到 节点2 和 节点3的距离。
- 源点到节点2的最短距离为1,小于原minDist[2]的数值max,更新minDist[2] = 1
- 源点到节点3的最短距离为4,小于原minDist[3]的数值max,更新minDist[3] = 4
可能有录友问:为啥和 minDist[2] 比较?
再强调一下 minDist[2] 的含义,它表示源点到节点2的最短距离,那么目前我们得到了源点到节点2的最短距离为1,小于默认值max,所以更新。 minDist[3]的更新同理



#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int main() {int n, m, p1, p2, val;cin >> n >> m;vector<vector<int>> grid(n + 1, vector<int>(n + 1, INT_MAX));for(int i = 0; i < m; i++){cin >> p1 >> p2 >> val;grid[p1][p2] = val;}int start = 1;int end = n;std::vector<int> minDist(n + 1, INT_MAX);std::vector<bool> visited(n + 1, false);minDist[start] = 0; //加上初始化vector<int> parent(n + 1, -1);for (int i = 1; i <= n; i++) {int minVal = INT_MAX;int cur = 1;for (int v = 1; v <= n; ++v) {if (!visited[v] && minDist[v] < minVal) {minVal = minDist[v];cur = v;}}visited[cur] = true;for (int v = 1; v <= n; v++) {if (!visited[v] && grid[cur][v] != INT_MAX && minDist[cur] + grid[cur][v] < minDist[v]) {minDist[v] = minDist[cur] + grid[cur][v];parent[v] = cur; // 记录边}}}// 输出最短情况for (int i = 1; i <= n; i++) {cout << parent[i] << "->" << i << endl;}
}
相关文章:

代码随想录算法训练营 Day58 图论Ⅷ 拓扑排序 Dijkstra
图论 题目 117. 软件构建 拓扑排序:给出一个有向图,把这个有向图转成线性的排序就叫拓扑排序。 当然拓扑排序也要检测这个有向图是否有环,即存在循环依赖的情况,因为这种情况是不能做线性排序的。所以拓扑排序也是图论中判断有向…...

实现单例模式的6种方法(Python)
目录 一. 基于模块的实现(简单,易用) 二. 重新创建时报错(不好用) 三. 只靠方法获取实例(不好用) 四. 类装饰器 五. 重写__new__方法 六. 元类 七. 总结 单例模式(Singleton Pattern)是一种设计模式,其核心目标是确保一个类…...

基于 STM32 的智慧农业温室控制系统设计与实现
摘要 本文提出一种基于 STM32 微控制器的智慧农业温室控制系统设计方案,通过集成多类型环境传感器、执行机构及无线通信模块,实现对温室内温湿度、光照、土壤湿度等参数的实时监测与自动调控。文中详细阐述硬件选型、电路连接及软件实现流程,并附关键代码示例,为智慧农业领…...

深度学习优化器相关问题
问题汇总 各类优化器SGDMomentumNesterovAdagardAdadeltaRMSpropAdam优化器 为什么Adam不一定最优而SGD最优的深度网络中loss除以10和学习率除以10等价吗L1,L2正则化是如何让模型变得稀疏的,正则化的原理L1不可导的时候该怎么办梯度消失和梯度爆炸什么原因ÿ…...

【免费】【无需登录/关注】度分秒转换在线工具
UVE Toolbox 功能概述 这是一个用于地理坐标转换的在线工具,支持两种转换模式: 十进制度 → 度分秒 度分秒 → 十进制度 使用方法 十进制度转度分秒 在"经度"输入框中输入十进制度格式的经度值(例如:121.46694&am…...

常见的垃圾回收算法原理及其模拟实现
1.标记 - 清除(Mark - Sweep)算法: 这是一种基础的垃圾回收算法。首先标记所有可达的对象,然后清除未被标记的对象。 缺点是会产生内存碎片。 原理: 如下图分配一段内存,假设已经存储上数据了 标记所有…...

fpga-编程线性序列机和状态机
一、线性序列机和有限状态机和(状态机-编程思想)的原理 序列机是什么:用计数器对时钟个数计数,根据相应时钟周期下的单个周期时间和计数个数可以确定某个时刻的时间,确定时间后再需要时间点转换电平! 采用…...

力扣面试150题--完全二叉树的节点个数
Day 51 题目描述 思路 根据完全二叉树的规律,完全二叉树的高度可以直接通过不断地访问左子树就可以获取,判断左右子树的高度: 1. 如果相等说明左子树是满二叉树, 然后进一步判断右子树的节点数(最后一层最后出现的节点必然在右子树中) 2. 如…...

Qt 多线程环境下的全局变量管理与密码安全
在现代软件开发中,全局变量的管理和敏感信息的保护是两个重要的课题。特别是在多线程环境中,不正确的全局变量使用可能导致数据竞争和不一致的问题,而密码等敏感信息的明文存储更是会带来严重的安全隐患。本文将介绍如何在 Qt 框架下实现一个…...

内网映射有什么作用,如何实现内网的网络地址映射到公网连接?
在网络环境中,内网映射是一项重要的技术,它允许用户通过外部网络访问位于内部网络中的设备或服务。如自己电脑上的程序提供他人使用,或在家远程管理公司办公OA等涉及不同网络间的通信和数据交互。nat123作为一款老牌的内网映射工具࿰…...

BLIP3-o:一系列完全开源的统一多模态模型——架构、训练与数据集
摘要 在近期关于多模态模型的研究中,将图像理解与生成统一起来受到了越来越多的关注。尽管图像理解的设计选择已经得到了广泛研究,但对于具有图像生成功能的统一框架而言,其最优模型架构和训练方案仍有待进一步探索。鉴于自回归和扩散模型在…...
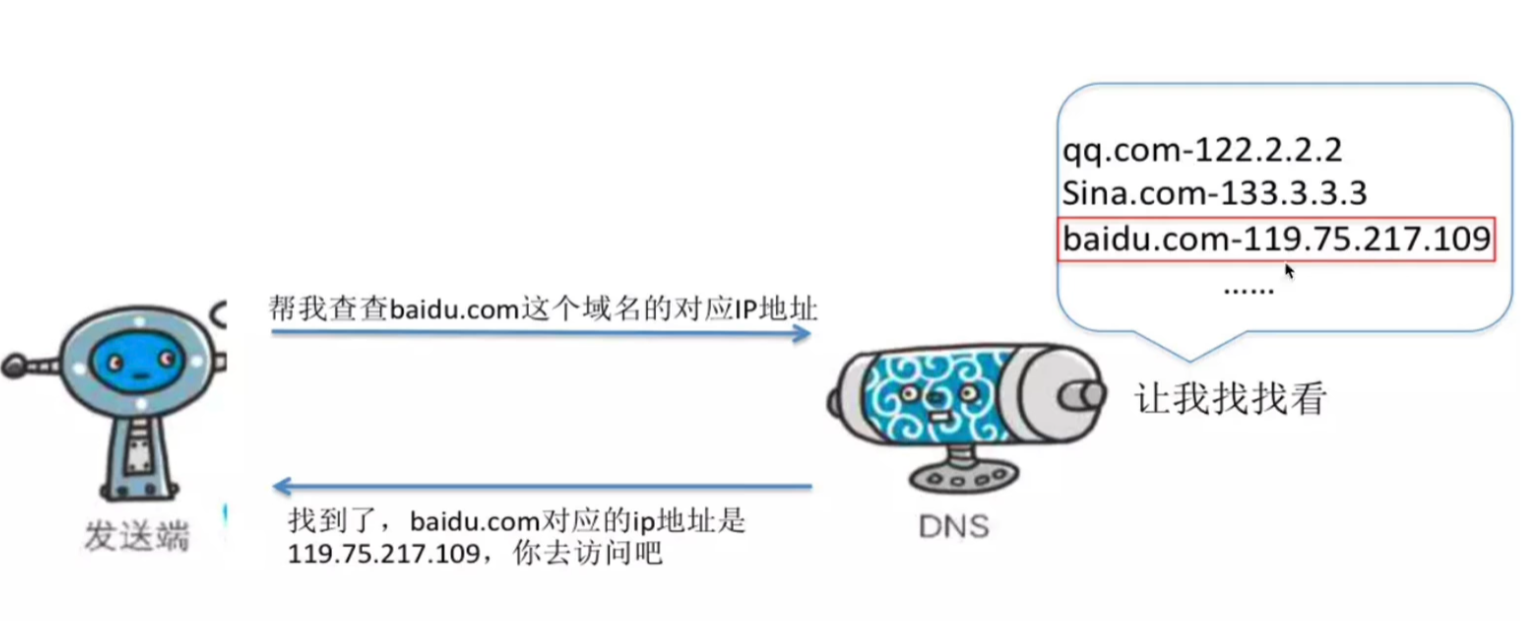
DNS解析流程入门篇
一、DNS 解析流程 1.1 浏览器输入域名 当在浏览器中输入 www.baidu.com 时,操作系统会按照以下步骤进行 DNS 解析: 检查本地 hosts 文件 :操作系统先检查本地的 /etc/hosts 文件,查看是否存在域名与 IP 地址的对应关系。如果找到…...

spring4第2课-ioc控制反转-依赖注入,是为了解决耦合问题
继续学习ioc控制反转, IOC(Inversion of Control)控制反转,也叫依赖注入, 目的是解决程序的耦合问题,轻量级spring的核心。 1.定义bean.xml <?xml version"1.0" encoding"UTF-8"…...

大模型系列22-MCP
大模型系列22-MCP 玩转 MCP 协议:用 Cline DeepSeek 接入天气服务什么是 MCP?环境准备:VScode Cline DeepSeek**配置 DeepSeek 模型:****配置 MCP 工具****uvx是什么?****安装 uv(会自动有 uvx 命令&…...

【监控】Prometheus+Grafana 构建可视化监控
在云原生和微服务架构盛行的今天,监控系统已成为保障业务稳定性的核心基础设施。作为监控领域的标杆工具,Prometheus和Grafana凭借其高效的数据采集、灵活的可视化能力,成为运维和开发团队的“标配”。 一、Prometheus Prometheus诞生于2012…...

vscode里几种程序调试配置
标题调试python嵌入的c代码,例如 import torch from torch.utils.cpp_extension import loadtest_load load(nametest_load, sources[test.cpp],extra_cflags[-O0, -g],#extra_cflags[-O1],verboseTrue, ) a torch.tensor([1, 2, 3]) b torch.tensor([4, 5, 6]) result te…...

RAGFlow源码安装操作过程
RAGFlow是一款基于深度文档理解构建的开源 RAG(Retrieval-Augmented Generation)引擎,可作为Dify的外部知识库使用[1]。本文主要介绍RAGFlow前端和后端等源码安装操作过程。 一.后端安装 特别注意:python ">3.12,<3…...

Unity使用XCharts动态配置数据——折线图(LineChart)
XCharts官网地址:https://xcharts-team.github.io/ 本地上传资源:https://download.csdn.net/download/m0_64375864/90919669 效果图: 动态配置数据: public class Test3 : MonoBehaviour {public LineChart lineChart;public …...

【HITCSAPP 哈工大计算机系统期末大作业】 程序人生-Hello’s P2P
计算机系统 大作业 题 目 程序人生-Hello’s P2P 专 业 计算机与电子通信类 学 号 2023112915 班 级 23L0505 学 生 杨昕彦 指 导 教 师 刘宏伟 计算机科学…...

DAY9 热力图和箱线图的绘制
浙大疏锦行 学会了绘制两个图: 热力图:表示每个特征之间的影响,颜色越深数值越大表示这两个特征的关系越紧密 箱线图:表示每个特征的数据分布情况 箱体(Box): 箱体的上下边界分别表示第一四分位…...

如何查看 GitLab 内置的 PostgreSQL 版本?
GitLab 依赖 PostgreSQL,PostgreSQL 的升级会随着 GitLab 的版本升级而进行,本文分享查看 GitLab 内置 PostgreSQL 版本的方法。 GitLab 版本和 PostgreSQL 版本需要一一对应,默认情况下使用 Omnibus 方式安装的 GitLab 实例会自动升级 Postg…...

VR 技术与病毒分离鉴定:一场奇妙的邂逅
过去,病毒分离鉴定主要依靠传统实验技术,虽为病毒学发展奠定基础,但在现代病毒研究中有诸多局限。 沉浸式操作,告别风险担忧 VR 技术给病毒分离鉴定带来的最大变革是大幅提升实验安全性。借助 VR 设备,实验者身处高…...

解释一下NGINX的反向代理和正向代理的区别?
大家好,我是锋哥。今天分享关于【解释一下NGINX的反向代理和正向代理的区别?】面试题。希望对大家有帮助; 解释一下NGINX的反向代理和正向代理的区别? NGINX的反向代理和正向代理的区别主要体现在它们的功能和使用场景上。下面我会详细解释它们的定义…...
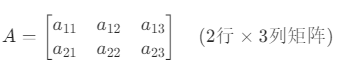
数学笔记一:标量、向量和矩阵基本概念辨析
一、标量 标量(Scalar) 是一种仅用数值大小(即 “量值”)就能完全描述的物理量或数学对象,它不具有方向属性。 例如在实数领域的正数、负数。 在物理学领域的多少斤、多少公斤、水温多少度、气温多少度都是标量。 …...

vue3获取两个日期之间的所有时间
1.获取两个日期之间所有年月日 如图所示: 代码如下: <template><div class"datePicker"><el-date-pickerv-model"value1"type"daterange"range-separator"至"start-placeholder"开始时间…...

Python 实现简易版的文件管理(结合网络编程)
目录 一、Python 代码实现1. 服务器端2. 客户端 二、结果展示1. 查看当前路径下的内容 ls2. 切换当前路径 cd3. 查看当前路径 pwd4. 显示根目录下的树状结构 tree5. 在当前路径下创建目录 mkdir6. 删除当前路径下的文件或目录 rm7. 复制文件 mv8. 移动文件 cp9. 用户从当前路径…...

元组可以比较大小吗?一次返回多个值?编程语言的元组?声明变量一定需要指定类型吗?
目录 元组可以比较大小吗? 一次返回多个值? 编程语言的元组 支持元组的语言 元组的基本特性 元组的初始化和使用 声明变量一定需要指定类型吗? var类型 元组可以比较大小吗? 不同编程语言对元组的定位稍有差异,是否可以比较大小随语言而定。 Swift支持…...

PXC集群
PXC集群 一、环境介绍二、PXC安装1、关闭默认mysql模块2、安装yum源3、准备pxc安装环境4、安装pxc5、启动mysql,并更改root密码 三、搭建PXC集群1、编辑/etc/my.cnf 配置文件(1)pxc1节点配置文件(2)pxc2节点配置文件&a…...

线程安全问题的成因
前言 大家晚上好呀~~ 今天学习了线程不安全问题的成因。线程安全问题是十分重要的知识点,我想把我所学的与大家分享一波,希望可以帮助到有需要的人,同时加深自己对于线程安全问题的理解。 分析过程如下 结语 今天心情还不错~ 要坚持持续…...

零基础远程连接课题组Linux服务器,安装anaconda,配置python环境(换源),在服务器上运行python代码【3/3 适合小白,步骤详细!!!】
远程连接服务器 请查阅之前的博客——零基础远程连接课题组Linux服务器,安装anaconda,配置python环境(换源),在服务器上运行python代码【1/3 适合小白,步骤详细!!!】&am…...
