华为OD机试真题——信道分配(2025B卷:200分)Java/python/JavaScript/C/C++/GO最佳实现

2025 B卷 200分 题型
本专栏内全部题目均提供Java、python、JavaScript、C、C++、GO六种语言的最佳实现方式;
并且每种语言均涵盖详细的问题分析、解题思路、代码实现、代码详解、3个测试用例以及综合分析;
本文收录于专栏:《2025华为OD真题目录+全流程解析+备考攻略+经验分享》
华为OD机试真题《信道分配》:
文章快捷目录
题目描述及说明
Java
python
JavaScript
C++
C
GO
题目名称:信道分配
- 知识点:贪心算法、逻辑处理
- 时间限制:1秒
- 空间限制:256MB
- 限定语言:不限
题目描述
算法工程师小明需要将通信用的信道分配给尽量多的用户,信道的条件及分配规则如下:
- 所有信道都有属性“阶”,阶为 ( r ) 的信道容量为 ( 2^r ) 比特。
- 所有用户需要传输的数据量相同,均为 ( D ) 比特。
- 一个用户可以分配多个信道,但每个信道只能分配给一个用户。
- 只有当分配给一个用户的所有信道容量之和 ( \geq D ) 时,用户才能传输数据。
输入描述:
- 第一行:一个数字 ( R ),表示最大阶数(( 0 \leq R < 20 ))。
- 第二行:( R+1 ) 个数字,表示每种信道的数量 ( N_i ),按阶从小到大排列(( 0 \leq N_i \leq 1000000 ))。
- 第三行:一个数字 ( D ),表示单个用户所需传输的数据量(( 0 < D < 1000000 ))。
输出描述:
一个数字,表示最多可以满足多少用户传输数据。
示例:
输入:
5
10 5 0 1 3 2
30
输出:
4
说明:通过合理分配信道,最多可满足4个用户的需求。
Java
问题分析
我们需要通过合理分配不同阶的信道,满足尽可能多的用户的数据传输需求。每个用户需要至少D比特的容量,每个阶为r的信道提供的容量为2^r。我们的目标是最大化满足的用户数量。
解题思路
- 贪心策略:优先处理能单独满足用户需求的高阶信道。
- 阶的容量判断:若某阶的单个信道容量≥D,则该阶所有信道都可直接分配给用户。
- 剩余容量处理:对于无法单独满足需求的信道,计算它们的总容量,并尽可能组合分配。
代码实现
import java.util.Scanner;public class Main {public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int R = scanner.nextInt(); // 最大阶数int[] num = new int[R + 1]; // 各阶信道的数量for (int i = 0; i <= R; i++) {num[i] = scanner.nextInt();}int D = scanner.nextInt(); // 用户需求int result = 0;// 处理所有能单独满足用户的高阶信道for (int r = R; r >= 0; r--) {long capacity = 1L << r; // 计算2^rif (capacity >= D) {result += num[r]; // 该阶所有信道均可单独使用num[r] = 0; // 标记为已用完}}// 计算剩余信道的总容量long totalCapacity = 0;for (int r = 0; r <= R; r++) {totalCapacity += (long) num[r] * (1L << r);}// 剩余容量可满足的用户数result += totalCapacity / D;System.out.println(result);}
}
代码解析
-
输入读取:
int R = scanner.nextInt();:读取最大阶数。int[] num = new int[R + 1];:存储各阶信道数量。int D = scanner.nextInt();:读取用户需求D。
-
处理高阶信道:
for (int r = R; r >= 0; r--) {long capacity = 1L << r; // 2^rif (capacity >= D) {result += num[r]; // 累加该阶信道数到结果num[r] = 0; // 标记为已用} }- 从最高阶到最低阶遍历,若当前阶的容量≥D,则所有该阶信道可单独满足用户。
-
计算剩余总容量:
long totalCapacity = 0; for (int r = 0; r <= R; r++) {totalCapacity += (long) num[r] * (1L << r); }- 遍历所有阶,累加剩余信道的总容量。
-
剩余容量分配:
result += totalCapacity / D;- 剩余总容量可满足的用户数为总容量除以D的商。
示例测试
-
示例1:
- 输入:
5 10 5 0 1 3 2 30 - 输出:
4 - 解析:高阶信道满足2个用户,剩余容量76满足2个用户,总计4。
- 输入:
-
示例2:
- 输入:
0 5 3 - 输出:
1 - 解析:所有信道容量总和5,满足1个用户。
- 输入:
-
示例3:
- 输入:
1 3 1 4 - 输出:
1 - 解析:总容量5满足1个用户。
- 输入:
综合分析
-
时间复杂度:
- 预处理高阶信道:O®,R为最大阶数(≤20),可忽略。
- 计算剩余总容量:O®。
- 总体时间复杂度:O®,极为高效。
-
空间复杂度:
- 使用数组存储各阶信道数量,空间复杂度为O®。
-
正确性保障:
- 高阶信道单独处理确保局部最优。
- 剩余容量总和整除D确保全局最优。
-
优势:
- 高效性:线性时间处理,适用于大输入规模。
- 简洁性:无需复杂数据结构,逻辑清晰。
-
适用场景:
- 需要快速分配资源以满足最大用户数的场景,如通信资源分配、云计算资源调度。
python
问题分析
我们需要分配不同阶的信道,使得尽可能多的用户能满足数据传输需求。每个用户需要至少D比特的容量,每个阶r的信道容量为2^r。目标是通过合理分配信道,最大化可以满足的用户数目。
解题思路
-
贪心策略:
- 处理高阶信道:单个信道容量≥D的高阶信道可直接满足用户,每个信道对应一个用户。
- 组合低阶信道:剩余的信道总容量可组合分配给用户,总容量除以D即为满足的用户数。
-
步骤:
- 预处理所有能单独满足用户的高阶信道。
- 计算剩余信道的总容量,并用该容量统计可满足的用户数。
代码实现
R = int(input相关文章:

华为OD机试真题——信道分配(2025B卷:200分)Java/python/JavaScript/C/C++/GO最佳实现
2025 B卷 200分 题型 本专栏内全部题目均提供Java、python、JavaScript、C、C++、GO六种语言的最佳实现方式; 并且每种语言均涵盖详细的问题分析、解题思路、代码实现、代码详解、3个测试用例以及综合分析; 本文收录于专栏:《2025华为OD真题目录+全流程解析+备考攻略+经验分…...

比亚迪“双剑”电池获中汽中心权威认证,堪称“移动安全堡垒”。
在新能源汽车发展中,电池安全是重中之重。比亚迪的刀片电池与闪充刀片电池提前通过电池新国标全项检测,获中汽中心权威认证,堪称“移动安全堡垒”。 传统电池极端条件下易热失控,而刀片电池独特长条形设计,似刀片般&am…...

【mysql】mysql的高级函数、高级用法
mysql是最常用的数据库之一,常见的函数用法大家应该都很熟悉,本文主要例举一些相对出现频率比较少的高级用法 (注:需注意mysql版本,大部分高级特性都是mysql8才有的) 多值索引与虚拟列 主要是解决字符串索引问题,光说…...

了解一下C#的SortedSet
基础概念 SortedSet 是 C# 中的一个集合类型,位于 System.Collections.Generic 命名空间下。它是一个自动排序的集合,用于存储不重复的元素,并且会根据元素的自然顺序(默认排序)或自定义比较器进行排序,内…...

【平面波导外腔激光器专题系列】用于光纤传感的低噪声PLC外腔窄线宽激光器
----翻译自Mazin Alalusi等人的文章 摘要 高性价比的 1550 nm DWDM平面外腔 (PLANEX) 激光器是干涉测量、布里渊、LIDAR 和其他光传感应用的最佳选择。其线宽<3kHz、低相位/频率噪声和极低的RIN。 简介 高性能光纤分布式传感技术是在过去几年中开发…...

Pytorch里面多任务Loss是加起来还是分别backward? | Pytorch | 深度学习
当你在深度学习中进入“多任务学习(Multi-task Learning)”的领域,第一道关卡可能不是设计网络结构,也不是准备数据集,而是:多个Loss到底是加起来一起backward,还是分别backward? 这个问题看似简单,却涉及PyTorch计算图的构建逻辑、自动求导机制、内存管理、任务耦合…...

K8S Pod调度方法实例
以下是一篇面向企业用户、兼具通俗易懂和实战深度的 Kubernetes Pod 调度方法详解博文大纲与正文示例。全文采用“图文(代码块)并茂 问答穿插 类比”方式,模拟了真实终端操作及输出,便于读者快速上手。 一、引言 为什么要关注 P…...

【mindspore系列】- 算子源码分析
本文会介绍mindspore的算子源码结构、执行过程以及如何编写一个自定义的mindspore算子。 源码介绍 首先,我们先从https://gitee.com/mindspore/mindspore/ 官网中clone源代码下来。 clone好代码后,可以看到源码的文件夹结构如下(只列出比较重要的文件夹): docsmindspore…...

学习日记-day17-5.27
完成目标: 知识点: 1.日期相关类_Calendar日历类 常用方法:int get(int field) ->返回给定日历字段的值void set(int field, int value) :将给定的日历字段设置为指定的值void add(int field, int amount) :根据日历的规则,为给定的日历字段添加或…...

一种比较精简的协议
链接地址为:ctLink: 一个比较精简的支持C/C的嵌入式通信的中间协议。 本文采用的协议格式如下 *帧头 uint8_t 起始字节:0XAF\ *协议版本 uint8_t 使用的协议版本号:当前为0X01\ *负载长度 uint8_t 数据段内容长…...

网络常识:网线和光纤的区别
网络常识:网线和光纤的区别 一. 介绍二. 网线2.1 什么是网线?2.2 网线的主要类别2.3 网线的优势2.4 网线的劣势 三. 光纤3.1 什么是光纤?3.2 光纤的主要类别3.3 光纤的优势3.4 光纤的劣势 四. 网线 vs 光纤:谁更适合你?…...

OpenCV CUDA模块图像过滤------创建一个 Scharr 滤波器函数createScharrFilter()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 该函数用于创建一个 Scharr 滤波器(基于 CUDA 加速),用于图像的一阶导数计算。它常用于边缘检测任务中&#…...
html css js网页制作成品——HTML+CSS+js醇香咖啡屋网页设计(5页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

[特殊字符] 构建高内聚低耦合的接口架构:从数据校验到后置通知的分层实践
在现代企业系统开发中,接口结构设计的质量直接影响系统的稳定性、扩展性与可维护性。随着业务复杂度上升,单一层次的接口实现往往难以应对功能膨胀、事务一致性、后置扩展等需求。因此,我们提出一种面向复杂业务场景的接口分层模型࿰…...

brep2seq 源码笔记2
数学公式是什么def forward(self, noise_1, noise_2, real_z_pNone): if(real_z_p): z_p_ self.downsample(real_z_p) input_2 z_p_ noise_2 z_f self.gen_z_f(input_2) output real_z_p z_f else: …...

UE5 蓝图,隐藏一个Actor,同时隐藏它的所有子物体
直接用actor.sethideningame是不行的 要先找到根组件,这样就有覆盖子物体的选项了...

人工智能AI之机器学习基石系列 第 2 篇:数据为王——机器学习的燃料与预处理
专栏系列:《人工智能AI之机器学习基石》② 高质量的数据是驱动机器学习模型的强大燃料 🚀 引言:无米之炊与数据的重要性 在上一篇文章《什么是机器学习?——开启智能之门》中,我们一起揭开了机器学习的神秘面纱&…...

代码随想录算法训练营 Day58 图论Ⅷ 拓扑排序 Dijkstra
图论 题目 117. 软件构建 拓扑排序:给出一个有向图,把这个有向图转成线性的排序就叫拓扑排序。 当然拓扑排序也要检测这个有向图是否有环,即存在循环依赖的情况,因为这种情况是不能做线性排序的。所以拓扑排序也是图论中判断有向…...

实现单例模式的6种方法(Python)
目录 一. 基于模块的实现(简单,易用) 二. 重新创建时报错(不好用) 三. 只靠方法获取实例(不好用) 四. 类装饰器 五. 重写__new__方法 六. 元类 七. 总结 单例模式(Singleton Pattern)是一种设计模式,其核心目标是确保一个类…...

基于 STM32 的智慧农业温室控制系统设计与实现
摘要 本文提出一种基于 STM32 微控制器的智慧农业温室控制系统设计方案,通过集成多类型环境传感器、执行机构及无线通信模块,实现对温室内温湿度、光照、土壤湿度等参数的实时监测与自动调控。文中详细阐述硬件选型、电路连接及软件实现流程,并附关键代码示例,为智慧农业领…...

深度学习优化器相关问题
问题汇总 各类优化器SGDMomentumNesterovAdagardAdadeltaRMSpropAdam优化器 为什么Adam不一定最优而SGD最优的深度网络中loss除以10和学习率除以10等价吗L1,L2正则化是如何让模型变得稀疏的,正则化的原理L1不可导的时候该怎么办梯度消失和梯度爆炸什么原因ÿ…...

【免费】【无需登录/关注】度分秒转换在线工具
UVE Toolbox 功能概述 这是一个用于地理坐标转换的在线工具,支持两种转换模式: 十进制度 → 度分秒 度分秒 → 十进制度 使用方法 十进制度转度分秒 在"经度"输入框中输入十进制度格式的经度值(例如:121.46694&am…...

常见的垃圾回收算法原理及其模拟实现
1.标记 - 清除(Mark - Sweep)算法: 这是一种基础的垃圾回收算法。首先标记所有可达的对象,然后清除未被标记的对象。 缺点是会产生内存碎片。 原理: 如下图分配一段内存,假设已经存储上数据了 标记所有…...

fpga-编程线性序列机和状态机
一、线性序列机和有限状态机和(状态机-编程思想)的原理 序列机是什么:用计数器对时钟个数计数,根据相应时钟周期下的单个周期时间和计数个数可以确定某个时刻的时间,确定时间后再需要时间点转换电平! 采用…...

力扣面试150题--完全二叉树的节点个数
Day 51 题目描述 思路 根据完全二叉树的规律,完全二叉树的高度可以直接通过不断地访问左子树就可以获取,判断左右子树的高度: 1. 如果相等说明左子树是满二叉树, 然后进一步判断右子树的节点数(最后一层最后出现的节点必然在右子树中) 2. 如…...

Qt 多线程环境下的全局变量管理与密码安全
在现代软件开发中,全局变量的管理和敏感信息的保护是两个重要的课题。特别是在多线程环境中,不正确的全局变量使用可能导致数据竞争和不一致的问题,而密码等敏感信息的明文存储更是会带来严重的安全隐患。本文将介绍如何在 Qt 框架下实现一个…...

内网映射有什么作用,如何实现内网的网络地址映射到公网连接?
在网络环境中,内网映射是一项重要的技术,它允许用户通过外部网络访问位于内部网络中的设备或服务。如自己电脑上的程序提供他人使用,或在家远程管理公司办公OA等涉及不同网络间的通信和数据交互。nat123作为一款老牌的内网映射工具࿰…...

BLIP3-o:一系列完全开源的统一多模态模型——架构、训练与数据集
摘要 在近期关于多模态模型的研究中,将图像理解与生成统一起来受到了越来越多的关注。尽管图像理解的设计选择已经得到了广泛研究,但对于具有图像生成功能的统一框架而言,其最优模型架构和训练方案仍有待进一步探索。鉴于自回归和扩散模型在…...
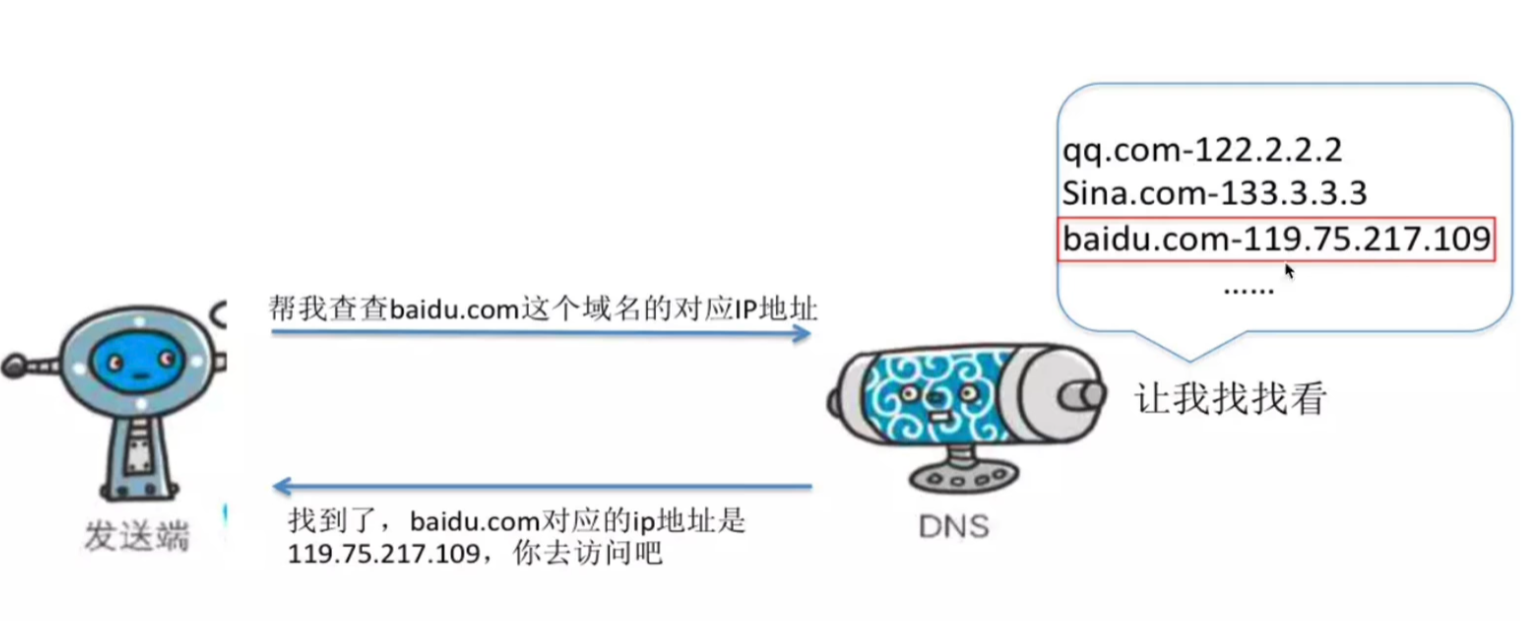
DNS解析流程入门篇
一、DNS 解析流程 1.1 浏览器输入域名 当在浏览器中输入 www.baidu.com 时,操作系统会按照以下步骤进行 DNS 解析: 检查本地 hosts 文件 :操作系统先检查本地的 /etc/hosts 文件,查看是否存在域名与 IP 地址的对应关系。如果找到…...

spring4第2课-ioc控制反转-依赖注入,是为了解决耦合问题
继续学习ioc控制反转, IOC(Inversion of Control)控制反转,也叫依赖注入, 目的是解决程序的耦合问题,轻量级spring的核心。 1.定义bean.xml <?xml version"1.0" encoding"UTF-8"…...
