数据结构7——二叉树
一、二叉树的定义与性质
1.定义
首先是树形结构,每个节点最多有2棵树,二叉树的子树有左右之分,不能颠倒。
2.性质
(1)二叉树的第i层,最多有2的(i-1)次幂。
(2)深度为k(层数也为k)的二叉树,最多有2^k-1结点。
(3)对于任意二叉树而言,若度为0的节点为N0个,度为2的节点为N2个,则:N0=N2+1。
二、二叉树的节点设计
1.采用顺序存储结构还是链式存储结构?
采用链式存储结构。
原因:顺序存储结构用数组实现,但对于数组来说,只适用于完全二叉树的情况,而对于一般的情况来说,浪费的空间较大。
2.二叉树(二叉链表)的有效节点设计
对于一个结点来说,最多有2个孩子,分别是左孩子和右孩子,所以设计二叉链表时,不仅需要设计该节点的值,而且还需要2个指针域,一个表示当前节点的左孩子,一个表示当前结点的右孩子。
typedef int ELEM_TYPE;
typedef struct Bin_Node
{ELEM_TYPE val;// 数据域struct Bin_Node* leftchild; //左孩子域struct Bin_Node* rightchild;//右孩子域
}Bin_Node;3.二叉树(二叉链表)的辅助结点的设计
让其辅助结点指向该二叉树的根节点位置。
typedef struct Bin_Tree{Bin_Node*root; //存放二叉树根节点的地址
}Bin_Tree; 三、二叉树的基本操作
1.二叉树的初始化
将二叉树的根节点置为空。
void Init(Bin_Tree* tree)
{assert(tree!=NULL);tree->root=NULL;// 将根节点置为空 } 2.购买新结点
(1)malloc申请空间,并判断空间是否申请成功。
(2)如果申请成功,则把其左孩子和右孩子指针置为空。
Bin_Node* BuyNode()
{//1.malloc申请空间Bin_Node*pnewnode=(Bin_Node*)malloc(sizeof(Bin_Node));if(pnewnode==NULL)exit(1);//将左孩子和右孩子置为空pnewnode->leftchild=pnewnode->rightchild=NULL; return pnewnode; } 3.二叉树的构建
3.1 用单个序列构造(此处使用先序)
(先序、中序、后序的一个,需要包含终止符#)
(1)先将根节点置为空。
(2)从键盘输入数据,判断数据是否为“#”
(3)如果不是,则购买结点,并为该节点赋值。对其左孩子和右孩子采用递归方法调用。
(4)如果是,则不断回退。
//采用先序遍历,使用递归实现
Bin_Node* Create_Bin_Tree1()
{//将根节点置为空 Bin_Node* root=NULL;ELEM_TYPE val;scanf("%d",&val);if(val!='#') //判断是否是终止符 {root=BuyNode(); //购买节点,并为结点赋值 root->val=val;root->leftchild=Create_Bin_Tree1(); //对其左右孩子采用递归方式实现 root->rightchild=Create_Bin_Tree1();} return root;
}3.2 用两个序列构造
(不需要包含终止符#,但都需要存在中序遍历)
3.2.1 采用先序和中序的遍历的方式
(1)首先定义一个节点,将该结点置为空。
(2)判断先序或者中序中元素的个数,如果个数为0,则不需要进行构造。
(3)个数大于0,则开始构造。
(4)购买一个结点,通过先序序列为该结点赋值,因为先序序列的第一个节点就是根节点。
(5)在中序序列找到当前结点的值,并返回下标。此时,根据此下标,可以将中序序列分为左右两个部分。
(6)对左右两个部分分别采用递归调用。
int Find_Pos(const char*in_str,ELEM_TYPE val) //在中序序列中找出val值所在的下标,进而将中序序列一分为二
{int count=0; //通过变量来返回位置 while(*in_str!=val){in_str++;count++;}return count;
}
Bin_Node* Create_Bin_Tree3_Pre_In(const char* pre_str, const char* in_str, int n)
{Bin_Node* pnewnode=NULL;if(n>0)//判断先序/中序的有效元素的个数 {//1.购买节点pnewnode=BuyNode();//2.为购买的节点赋值pnewnode->val=pre_str[0];//因为先序序列的第一个节点就是根节点//3.根据penwnode的值将中序划分为左右两个部分int index=Find_Pos(in_str,pre_str[0]);//4.将问题规模缩小化,采用递归的方式pnewnode->leftchild=Create_Bin_Tree3_Pre_In(pre_str+1,in_str,index);pnewnode->rightchild=Create_Bin_Tree3_Pre_In(pre_str+1+index,in_str+index+1,n-index-1); }return pnewnode;}3.2.2 采用中序和后序的遍历的方式
(1)首先定义一个节点,将该结点置为空。
(2)判断后序或者中序中元素的个数,如果个数为0,则不需要进行构造。
(3)个数大于0,则开始构造。
(4)购买一个结点,通过后序序列为该结点赋值,因为后序序列的最后一个节点就是根节点。
(5)在中序序列找到当前结点的值,并返回下标。此时,根据此下标,可以将中序序列分为左右两个部分。
(6)对左右两个部分分别采用递归调用。
int Find_Pos(const char*in_str,ELEM_TYPE val) //在中序序列中找出val值所在的下标,进而将中序序列一分为二
{int count=0; //通过变量来返回位置 while(*in_str!=val){in_str++;count++;}return count;
}Bin_Node* Create_Bin_Tree3_In_Post(const char* in_str, const char* post_str, int n)
{Bin_Node*pnewnode=NULL;if(n>0) //存在有效的个数{pnewnode=BuyNode();//购买节点pnewnode->val=post_str[n-1];//通过后序遍历得到根节点//根据pnewnode的值将中序序列划分为左右两个部分 int index=Find_Pos(in_str,pnewnode->val);//将问题规模缩小化,采用递归的方式pnewnode->leftchild=Create_Bin_Tree3_In_Post(in_str,post_str,index) ;pnewnode->rightchild=Create_Bin_Tree3_In_Post(in_str+index+1,post_str+index,n-index-1);} return pnewnode;
}4.二叉树的遍历(非递归实现)
4.1 二叉树的先序遍历 (根左右)
(1)申请一个栈,然后将根节点入栈。
(2)while循环判断栈是否为空,如果栈不为空,取出栈顶元素值。
(3)判断其左右孩子是否存在,如果存在,则先将右孩子压入栈,然后在将左孩子压入栈。
(4)直到栈为空(while结束为止)
void Preorder(Bin_Tree* tree)
{//assert(tree!=NULL);//申请一个栈,将根节点入栈std::stack<Bin_Node*> st;st.push(tree->root);//判断栈是否为空while(!st.empty()){//取出栈顶元素的值Bin_Node*p=st.top();st.pop();//打印printf("%d",p->val); //先判断其右孩子是否存在,存在则入栈if(p->rightchild!=NULL){st.push(p->rightchild);}//判断其左孩子是否存在,存在则入栈 if(p->leftchild!=NULL){st.push(p->leftchild);} } }
4.2 二叉树的中序遍历(左根右)
(1)先申请一个栈,将根节点压入栈中。
(2)设置一个标记位:判断当前结点是新插入的结点还是老结点。
(3)如果是新插入的节点,则判断其左孩子是否存在,存在则将左孩子压入栈中,直到左孩子为空。
(4)此时,已经将最左边的全部压入栈中,将当前的栈顶结点出栈,并打印栈顶元素的值。
(5)判断当前节点的右孩子是否存在,存在则将右孩子压入栈中,此时更改标记位为新插入的结点。
(6)如果右孩子不存在,则更改标记位为老节点。
(7)直到栈为空结束。
void Inorder(Bin_Tree* tree)
{//assertassert(tree->root!=NULL);//申请一个栈std::stack<Bin_Node*> st;//将根节点入栈st.push(tree->root);//定义一个标记位bool tag=true; //表示是刚插入的结点 while(!st.empty()){//判断当前节点是刚插入的结点还是老结点 while(tag&&st.top()->leftchild!=NULL) //是新结点且左孩子不为空 {//将左孩子入栈st.push(st.top()->leftchild); }//此时,获取栈顶元素的值Bin_Node* p=st.top() ;st.pop();printf("%d ",p->val);//判断其右孩子是否存在if(p->rightchild!=NULL){//存在则将右孩子入栈,并更改标记位st.push(p->rightchild);tag=true; }else{tag=false;} }} 4.3 二叉树的后序遍历(左右根)
4.3.1 双栈法实现
(1)先申请两个栈,s1和s2。其中s2表示结点的访问顺序。将根节点压入到s1中。
(2)判断s1是否为空,如果不为空,则将当前节点取出,压入到s2中,并判断当前结点的左右孩子是否存在,如果存在,则将其压入到s1中。
(3)重复执行,直到s1为空,此时,将s2中各节点的元素值打印出来。
void PostOrder(Bin_Tree* tree)
{//申请两个栈 S1 S2 std::stack<Bin_Node*> s1,s2;//将根节点压入到S1中s1.push(tree->root) ;//判断S1是否为空Bin_Node*p=NULL;while(!s1.empty()) {p=s1.top();//获取当前的栈顶元素 s1.pop() ;s2.push(p);//将结点压入到S2中if(p->leftchild!=NULL) //判断左孩子是否为空 {s1.push(p->leftchild);}if(p->rightchild!=NULL) //判断右孩子是否为空 {s1.push(p->rightchild);} }//此时,s1为空,则将S2中的元素逐个打印while(!s2.empty()) {printf("%d ",s2.top()->val);s2.pop();}} 4.3.2 单栈法实现
(1)申请一个栈,将根节点入栈。
(2)栈不为空时,先去判断当前结点是新结点还是老结点,如果是新结点再判断其左孩子是否存在,如果存在则将左孩子压入栈中。
(3)如果左孩子不存在或者当前结点是老节点,则去判断当前节点是否存在右孩子,如果右孩子存在,则将右孩子压入栈。右孩子不存在或者右孩子是老结点,则将该节点的元素值打印出来,并让当前指针指向该结点。
void PostOrder1(Bin_Tree* tree)
{assert(tree!=NULL);//1.申请一个栈std::stack<Bin_Node*> st;st.push(tree->root);//定义一个标记位,用来遍历最左边的结点bool tag=true; //定义一个指针,用来记录右边刚被访问的节点Bin_Node* preNode=NULL; //2.判断栈是否为空while(!st.empty()){//判断是否是新结点以及其左孩子是否存在while(tag&&st.top()->leftchild!=NULL){st.push(st.top()->leftchild);//将左孩子压入到栈中 }//此时左边已经结束 ,判断右孩子是否存在if(st.top()->rightchild==NULL||st.top()->rightchild==preNode){Bin_Node*p=st.top();st.pop();printf("%d ",p->val);preNode=p;tag=false;}else //右孩子存在,则将右孩子入栈 {st.push(st.top()->rigthchild);tag=true;// 只要有入栈的操作则表示是新结点,需要更改标记位 }} } 4.4 二叉树的层序(层次)遍历
(1)申请一个队列,并将根节点入队。
(2)循环判断队列是否为空。
(3)如果队列不为空,则获取队头元素,并将队头元素出队,接着判断其左右孩子是否存在,如果存在,则将左右孩子入队。
(4)如果为空,则结束。
void Level_Traversal(Bin_Node* root)
{//先申请一个队列 std::queue<Bin_Node*> q;//将根节点入队 q.push(root);//循环判断根节点是否为空 while(!q.empty()){Bin_Node*p=q.front();//获取队头元素 q.pop();printf("%d ",p->val);//判断其左右孩子是否存在if(p->leftchild!=NULL){q.push(p->leftchild);} if(p->rightchild!=NULL){q.push(p->rightchild);}}
}4.5 二叉树的正S遍历
(1)申请两个栈,栈s1,s2。
(2)将根节点入栈到s1中。
(3)只要两个栈中,一个不为空,则入栈。
(4)判断哪个栈不为空,如果栈1不为空,则将栈1中的元素取出,并按照从右向左的顺序判断其左右孩子是否存在,如果存在,则将右孩子和左孩子分别入栈2。直到栈1为空,停止。
(5)如果栈2不为空,则将栈2中的元素取出,并按照从左向右的顺序判断其左右孩子是否存在,如果存在,则将左孩子和右孩子分别入栈1。直到栈2为空,停止。
(6)如此循环,直到栈1和栈2均为空为止。
void S_Level_Traversal(Bin_Node* root)
{//申请两个栈 std::stack<Bin_Node*> st1,st2;//将根节点入栈1st1.push(root);//while循环while(!st1.empty()||!st2.empty()){while(!st1.empty()) //栈1不为空 {//取出栈中的元素值Bin_Node*p=st1.top();st1.pop();printf("%d ",p->val); //按照从右向左的顺序判断其孩子是否存在,存在则将孩子压入栈2中if(p->rightchild!=NULL){st2.push(p->rightchild);} if(p->leftchild!=NULL){st2.push(p->leftchild);}}while(!st2.empty()) //栈2不为空,则取出元素的值{Bin_Node*p=st2.top() ;st2.pop();printf("%d ",p->val);//按照从左向右的顺序判断其孩子是否存在,存在则将孩子压入栈1中if(p->leftchild!=NULL) {st1.push(p->leftchild);}if(p->rightchild!=NULL){st1.push(p->rightchild);}} }
}4.6 二叉树的倒S遍历
(1)申请两个栈,栈s1,s2。
(2)将根节点入栈到s1中。
(3)只要两个栈中,一个不为空,则入栈。
(4)判断哪个栈不为空,如果栈1不为空,则将栈1中的元素取出,并按照从左向右的顺序判断其左右孩子是否存在,如果存在,则将左孩子和右孩子分别入栈2。直到栈1为空,停止。
(5)如果栈2不为空,则将栈2中的元素取出,并按照从右向左的顺序判断其左右孩子是否存在,如果存在,则将右孩子和左孩子分别入栈1。直到栈2为空,停止。
(6)如此循环,直到栈1和栈2均为空为止。
void Reverse_S_Level_Traversal(Bin_Node* root)
{//申请两个栈 std::stack<Bin_Node*> st1,st2;//将根节点入栈1st1.push(root);//while循环while(!st1.empty()||!st2.empty()){while(!st1.empty()) //栈1不为空 {//取出栈中的元素值Bin_Node*p=st1.top();st1.pop();printf("%d ",p->val); //按照从左向右的顺序判断其孩子是否存在,存在则将孩子压入栈2中if(p->leftchild!=NULL){st2.push(p->leftchild);}if(p->rightchild!=NULL){st2.push(p->rightchild);} }while(!st2.empty()) //栈2不为空,则取出元素的值{Bin_Node*p=st2.top() ;st2.pop();printf("%d ",p->val);//按照从右向左的顺序判断其孩子是否存在,存在则将孩子压入栈1中if(p->rightchild!=NULL){st1.push(p->rightchild);}if(p->leftchild!=NULL) {st1.push(p->leftchild);}} }
}5. 二叉树的销毁 (非递归)
(1)申请一个栈,将根节点入栈
(2)判断栈是否为空,如果为空,则结束。
(3)如果不为空,则将栈顶元素出栈,判断其左右孩子是否为空,如果不为空,则将左右孩子入栈。
(4)直到栈空结束。
void Destroy1(Bin_Tree* pTree)//非递归
{//申请一个栈 std::stack<Bin_Node*> st;st.push(pTree->root);//将根节点入栈 while(!st.empty()){Bin_Node*p=st.top();st.pop();//将栈顶结点出栈 if(p->leftchild!=NULL) //判断其左右孩子是否存在 {st.push(p->leftchild); }if(p->rightchild!=NULL){st.push(p->rightchild);}free(p);//释放该节点 }
}相关文章:

数据结构7——二叉树
一、二叉树的定义与性质 1.定义 首先是树形结构,每个节点最多有2棵树,二叉树的子树有左右之分,不能颠倒。 2.性质 (1)二叉树的第i层,最多有2的(i-1)次幂。 (2)深度为k࿰…...

从“被动养老”到“主动健康管理”:平台如何重构代际关系?
在老龄化与数字化交织的背景下,代际关系的重构已成为破解养老难题的关键。 传统家庭养老模式中,代际互动多表现为单向的“赡养-被赡养”关系。 而智慧养老平台的介入,通过技术赋能、资源整合与情感连接,正在推动代际关系向“协作…...

Java 中的 synchronized 和 Lock:如何保证线程安全
Java 中的 synchronized 和 Lock:如何保证线程安全 引言 在 Java 多线程编程中,线程安全是一个核心问题。当多个线程同时访问共享资源时,可能会导致数据不一致或其他不可预期的结果。synchronized关键字和Lock接口是 Java 中实现线程同步的…...

贪心算法应用:最大匹配问题详解
Java中的贪心算法应用:最大匹配问题详解 贪心算法是一种在每一步选择中都采取当前状态下最优的选择,从而希望导致结果是全局最优的算法策略。在Java中,贪心算法可以应用于多种问题,其中最大匹配问题是一个经典的应用场景。下面我将从基础概念到具体实现,全面详细地讲解贪…...

爬虫IP代理效率优化:策略解析与实战案例
目录 一、代理池效率瓶颈的根源分析 二、六大核心优化策略 策略1:智能IP轮换矩阵 策略2:连接复用优化 策略3:动态指纹伪装 策略4:智能重试机制 三、典型场景实战案例 案例1:电商价格监控系统 案例2:…...

豆瓣电视剧数据工程实践:从爬虫到智能存储的技术演进(含完整代码)
通过网盘分享的文件:资料 链接: https://pan.baidu.com/s/1siOrGmM4n-m3jv95OCea9g?pwd4jir 提取码: 4jir 1. 引言 1.1 选题背景 在影视内容消费升级背景下,豆瓣电视剧榜单作为国内最具影响力的影视评价体系,其数据价值体现在:…...
的漏洞特征流量特征)
【HW系列】—C2远控服务器(webshell链接工具, metasploit、cobaltstrike)的漏洞特征流量特征
文章目录 蚁剑、冰蝎、哥斯拉一、蚁剑(AntSword)流量特征二、冰蝎(Behinder)流量特征三、哥斯拉(Godzilla)流量特征 metasploit、cobaltstrike一、Metasploit流量特征二、CobaltStrike流量特征三、检测与防…...

5.28 孔老师 nlp讲座
本次讲座主要介绍了语言模型的起源、预训练模型以及大语言模型(需要闫老师后讲)等内容。首先,语言模型的起源可以追溯到语音识别中的统计语言模型,通过估计声学参数串产生文字串的概率来找到最大概率的文字串。然后,介…...

基于微信小程序的漫展系统的设计与实现
博主介绍:java高级开发,从事互联网行业六年,熟悉各种主流语言,精通java、python、php、爬虫、web开发,已经做了六年的毕业设计程序开发,开发过上千套毕业设计程序,没有什么华丽的语言࿰…...

打卡day39
一、 图像数据的介绍 1.1 灰度图像 # 先继续之前的代码 import torch import torch.nn as nn import torch.optim as optim from torch.utils.data import DataLoader , Dataset # DataLoader 是 PyTorch 中用于加载数据的工具 from torchvision import datasets, transforms…...

基于Web的分布式图集管理系统架构设计与实践
引言:为什么需要分布式图集管理? 在现代Web图形应用中,纹理图集(Texture Atlas)技术是优化渲染性能的关键手段。传统的图集制作流程通常需要美术人员使用专业工具(如TexturePacker)离线制作&am…...

mysql执行sql语句报错事务锁住
报错情况 1205 - Lock wait timeout exceeded; try restarting transaction先找出长时间运行的事务 SELECT * FROM information_schema.INNODB_TRX ORDER BY trx_started ASC;终止长时间运行的事务 KILL [PROCESS_ID];...

Java消息队列应用:Kafka、RabbitMQ选择与优化
Java消息队列应用:Kafka、RabbitMQ选择与优化 在Java应用领域,消息队列是实现异步通信、应用解耦、流量削峰等重要功能的关键组件。Kafka和RabbitMQ作为两种主流的消息队列技术,各有特点和适用场景。本文将深入探讨Kafka和RabbitMQ在Java中的…...

零基础设计模式——结构型模式 - 组合模式
第三部分:结构型模式 - 组合模式 (Composite Pattern) 在学习了桥接模式如何分离抽象和实现以应对多维度变化后,我们来探讨组合模式。组合模式允许你将对象组合成树形结构来表现“整体-部分”的层次结构。组合模式使得用户对单个对象和组合对象的使用具…...

额度年审领域知识讲解
金融领域的“额度年审”是一个非常重要的常规性工作。它指的是金融机构(主要是银行)对其授予客户的各种信用额度或授信额度,在授信有效期内(通常是一年)进行周期性的重新评估、审查和确认的过程。 核心目的࿱…...

腾讯云国际站可靠性测试
在数字化转型加速的今天,企业对于云服务的依赖已从“可选”变为“必需”。无论是跨境电商的实时交易,还是跨国企业的数据协同,云服务的可靠性直接决定了业务连续性。作为中国领先的云服务提供商,腾讯云国际站(Tencent …...

自定义异常小练习
在开始之前,让我们高喊我们的口号: 键盘敲烂,年薪百万! 目录 键盘敲烂,年薪百万! 异常综合练习: 自定义异常 异常综合练习: 自定义异常: 定义异常类写继承关系空参构造带参构造 自定…...

SpringBoot整合MinIO实现文件上传
使用Spring Boot与JSP和MinIO(一个开源对象存储系统,兼容Amazon S3)进行集成,您可以创建一个Web应用来上传、存储和管理文件。以下是如何将Spring Boot、JSP和MinIO集成的基本步骤: 这个是minio正确启动界面 这个是min…...

基于面向对象设计的C++日期推算引擎:精准高效的时间运算实现与运算重载工程化实践
前引: 在软件开发中,时间与日期的处理是基础但极具挑战性的任务。传统的手工日期运算逻辑往往面临闰年规则、月份天数动态变化、时区转换等复杂场景的容错难题,且代码冗余度高、可维护性差。本文将深入探讨如何利用C的面向对象特性与成员函数…...
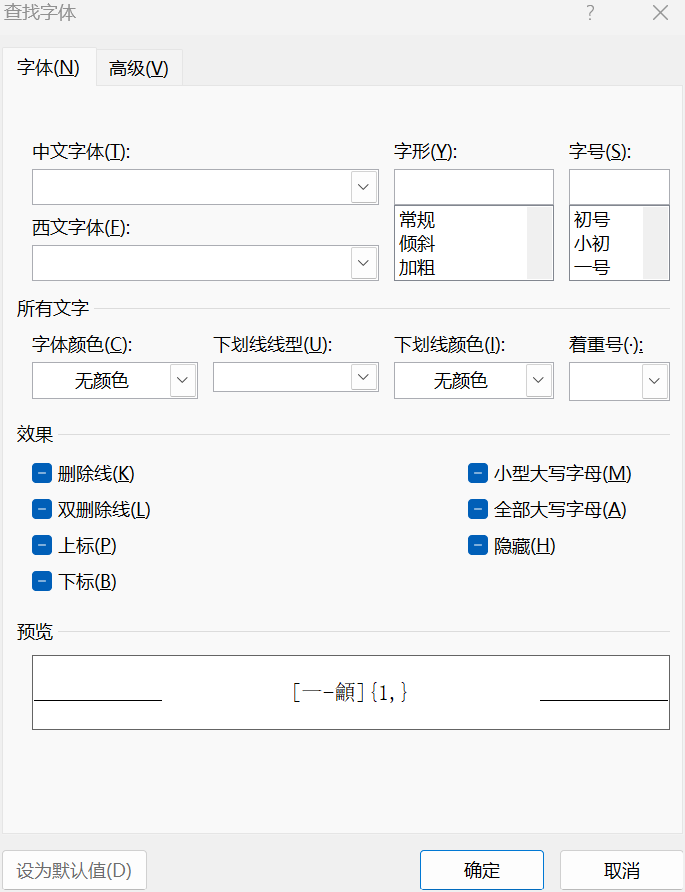
如何把 Microsoft Word 中所有的汉字字体替换为宋体?
Ctrl H ,然后,点击更多,勾选使用通配符,查找内容中填入 [一-龥]{1,}, 这是 Word 通配符匹配汉字的经典写法(匹配 Unicode 范围内的 CJK 汉字)。 然后, “替换为”留空,点…...
02. [Python+Golang+PHP]三数之和,多种语言实现最优解demo
一、问题描述:三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请你返回所有和为 0 且不重复的三元组。 注意:答案中…...

MongoDB选择理由
1.简介 MongoDB是一个基于分布式文件存储的数据库由C语言编写,旨在为WEB应用提供可扩展的高性能数据存储解决方案。MongoDB是一个介于关系数据库和非关系数据库之间的产品,是非关系数据库当中功能最丰富,最像关系数据库的。Mongo最大的特点是…...

倚光科技在二元衍射面加工技术上的革新:引领光学元件制造新方向
倚光科技二元衍射面加工技术(呈现出细腻的光碟反射纹路) 在光学元件制造领域,二元衍射面的加工技术一直是行业发展的关键驱动力之一。其精准的光相位调制能力,在诸多前沿光学应用中扮演着不可或缺的角色。然而,长期以来…...

驱动开发(2)|鲁班猫rk3568简单GPIO波形操控
上篇文章写了如何下载内核源码、编译源码的详细步骤,以及一个简单的官方demo编译,今天分享一下如何根据板子的引脚写自己控制GPIO进行高低电平反转。 想要控制GPIO之前要学会看自己的引脚分布图,我用的是鲁班猫RK3568,引脚分布图如…...

《软件工程》第 3 章 -需求工程概论
在软件工程的开发流程中,需求工程是奠定项目成功基础的关键环节。它专注于获取、分析、定义和管理软件需求,确保开发出的软件能真正满足用户需求。接下来,我们将按照目录内容,结合 Java 代码和实际案例,深入讲解需求工…...

VMware-MySQL主从
MySQL主从 服务器信息 服务器类型角色主机地址主机名称虚拟机master192.168.40.128test-1虚拟机slave192.168.40.129test-2 Master 配置(192.168.40.128) 删除自动生成的配置 /var/lib/mysql/auto.cnf [roottest-1 ~]# rm -rf /var/lib/mysql/auto.…...

ArcGIS Pro 3.4 二次开发 - 几何
环境:ArcGIS Pro SDK 3.4 + .NET 8 文章目录 几何1 空间参考1.1 从已知ID构建空间参考1.2 从字符串构建空间参考1.3 使用 WGS84 空间参考1.4 使用已知ID构建带有垂直坐标系的空间参考1.5 使用垂直坐标系从字符串构建SpatialReference1.6 使用自定义投影坐标系(PCS)构建空间参…...

2023-ICLR-ReAct 首次结合Thought和Action提升大模型解决问题的能力
关于普林斯顿大学和Google Research, Brain Team合作的一篇文章, 在语言模型中协同Reasoning推理和Action行动。 论文地址:https://arxiv.org/abs/2210.03629 代码:https://github.com/ysymyth/ReAct.git 其他复现 langchain :https://pytho…...

Rust 开发的一些GUI库
最近考虑用Rust干点什么,于是搜集了下资料——根据2025年最新调研结果和社区实践,Rust GUI库生态已形成多个成熟度不同的解决方案。以下是当前主流的GUI库分类及特点分析,结合跨平台支持、开发体验和实际应用场景进行综合评估: 一…...

【第四十六周】文献阅读:从 RAG 到记忆:大型语言模型的非参数持续学习
目录 摘要Abstract从 RAG 到记忆:大型语言模型的非参数持续学习研究背景方法论1. 离线索引(Offline Indexing)2. 在线检索(Online Retrieval)具体细节 创新性实验结果局限性总结 摘要 本论文旨在解决当前检索增强生成…...
