算法日记32:埃式筛、gcd和lcm、快速幂、乘法逆元
一、埃式筛(计算质数)
1.1、概念
1.1.1、在传统的计算质数中,我们采用单点判断,即判断(2~sqrt(n))是否存在不合法元素,若存在则判否,否则判是

1.1.2、假设,此时我们需要求1~1000的所有质数,此方法的时间复杂度就会变成O(n*sqrt(n)),这显然太过冗余了

- 因此,我们可以使用埃式筛
1.1.3、现在,求1~20中的所有质数,我们就可以:
-
1)首先将0、1排除:
-
2)创建从2到n的连续整数列表,[2,3,4,…,n];
-
3)初始化 p = 2,因为2是最小的质数;
-
4)枚举所有p的倍数(2p,3p,4p,…),标记为非质数(合数);
-
5)找到下一个 没有标记 且 大于p 的数。如果没有,结束运算;如果有,将该值赋予p,重复步骤4;
-
6)运算结束后,剩下所有未标记的数都是找到的质数。

-
此时,
2是第一个质数,因此把2的倍数全部设置为1(vis[j]=1)将其全部筛出

-
接下来,发现
3为0,表示3是一个质数,因此我们把3的倍数也给筛掉

-
因此,我们可以发现只要其没有被其他数字筛掉,那么他就一定是质数
1.2、总结:

ll vis[N];//用来判断一个数是否被筛掉了,0->没被筛掉,1->筛掉
void solve()
{ll n;cin>>n;vis[0]=vis[1]=1;for(ll i=2;i<=n;i++)//从2开始筛值{//从i*2开始,每次+i,当枚举到还没筛掉的数,筛掉for(ll j=i*i;j<=n;j+=i) {if(vis[i]==0) vis[j]=1;}}for(ll i=2;i<=n;i++) if(vis[i]==0) cout<<i<<' ';
}
2、最大公约数(gcd)和最小公倍数(lcm)
2.1、gcd求法
2.1.1、如何求解两个数(a,b)的最大公约数(gcd)?
- 使用辗转相除法
- 首先 ,我们假设(a>b),通过数学公式不难得出:
- 1)
gcd(a,b)=gcd(a%b,b),比如gcd(18,6)=gcd(0,6) - 2)
if(b==0)那么意味着此时的a即为最小公倍数
- 因此,代码可以写成
ll gcd(ll a,ll b) //只需记住,无论何时:a>b
{return b==0 ? a : gcd(b,a%b);
}

2.2、lcm求法
2.2.1、如何求解两个数(a,b)的最小公倍数(lcm)?
- 只需记住一个公式即可:
a*b=gcd(a,b)*lcm(a*b);
3、快速幂
3.1、概念:求解ab
- 1、当
b为奇数时候,拆出一个a,此时,b就变成了一个偶数 - 2、当
b为一个偶数的时候,就拆出其次方项b-->2/b

3.1.1、代码实现
//快速幂
ll qmi(ll a,ll b,ll c) //a ^ b % c
{int res=1;while(b){if(b&1) res=res*a%c,b--;//当b是奇数时,拆出一个a,使得 b 变成偶数else a=a*a%c,b>>=1; //此时b为偶数,拆出一个a*a,等待下次为奇数再计算答案}return res;
}
四、乘法逆元
4.1、概念
- 在写题目的时候,假设我们需要表达
a/b,是不好表达的,只能用浮点数来表示,因此我们就采用乘法逆元(类似于倒数 % p)来表示

4.2、那么,如何来求逆元呢?
- 我们可以使用费马小定理来求解

4.3、乘法逆元例题
- 题目链接

4.3.1、对于例题,我们可以对这个分式进行分解

- 因此,我们可以使用逆元来表示分数即可
#include<bits/stdc++.h>
using namespace std;typedef long long ll;
const int N = 2e5 + 7;
ll p=998244353;ll qmi(ll a,ll b) //快速幂
{ll res=1;while(b){if(b&1) res=res*a%p,b--;a=a*a%p,b>>=1;}return res%p;
}ll inv(int x) //求解x的逆元
{return qmi(x,p-2)%p;
}void solve()
{ll a,b,c,q;cin>>a>>b>>c>>q;while(q--){ll x;cin>>x;cout<<(a*x%p+b)%p*inv(c*x%p)%p<<'\n'; }
}int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int _ = 1; cin>>_;while (_--) solve();return 0;
}
相关文章:

算法日记32:埃式筛、gcd和lcm、快速幂、乘法逆元
一、埃式筛(计算质数) 1.1、概念 1.1.1、在传统的计算质数中,我们采用单点判断,即判断(2~sqrt(n))是否存在不合法元素,若存在则判否,否则判是 1.1.2、假设,此时我们需要求1~1000的所有质数&am…...

黑马点评-分布式锁Lua脚本
文章目录 分布式锁Redis setnxredis锁误删Lua脚本 分布式锁 当我们的项目服务器不只是一台(单体),而是部署在多态服务器上(集群/分布式),同样会出现线程安全问题。不同服务器内部有不同的JVM,每…...

P7-大规模语言模型分布式训练与微调框架调研文档
1. 引言 随着大语言模型(LLMs)在自然语言处理(NLP)、对话系统、文本生成等领域的广泛应用,分布式训练和高效微调技术成为提升模型性能和部署效率的关键。分布式训练框架如 Megatron-LM 和 DeepSpeed 针对超大规模模型…...

机械师安装ubantu双系统:三、GPT分区安装Ubantu
目录 一、查看磁盘格式 二、安装ubantu 参考链接: GPT分区安装Ubuntu_哔哩哔哩_bilibili 一、查看磁盘格式 右击左边灰色区域,点击属性 二、安装ubantu 插入磁盘,重启系统,狂按F7(具体我也忘了)&#…...

ORM++ 封装实战指南:安全高效的 C++ MySQL 数据库操作
ORM 封装实战指南:安全高效的 C MySQL 数据库操作 一、环境准备 1.1 依赖安装 # Ubuntu/Debian sudo apt-get install libmysqlclient-dev # CentOS sudo yum install mysql-devel# 编译时链接库 (-I 指定头文件路径 -L 指定库路径) g main.cpp -stdc17 -I/usr/i…...

kafka学习笔记(三、消费者Consumer使用教程——从指定位置消费)
1.简介 Kafka的poll()方法消费无法精准的掌握其消费的起始位置,auto.offset.reset参数也只能在比较粗粒度的指定消费方式。更细粒度的消费方式kafka提供了seek()方法可以指定位移消费允许消费者从特定位置(如固定偏移量、时间戳或分区首尾)开…...

【后端高阶面经:架构篇】46、分布式架构:如何应对高并发的用户请求
一、架构设计原则:构建可扩展的系统基石 在分布式系统中,高并发场景对架构设计提出了极高要求。 分层解耦与模块化是应对复杂业务的核心策略,通过将系统划分为客户端、CDN/边缘节点、API网关、微服务集群、缓存层和数据库层等多个层次,实现各模块的独立演进与维护。 1.1 …...

网络编程学习笔记——TCP网络编程
文章目录 1、socket()函数2、bind()函数3、listen()4、accept()5、connect()6、send()/write()7、recv()/read()8、套接字的关闭9、TCP循环服务器模型10、TCP多线程服务器11、TCP多进程并发服务器 网络编程常用函数 socket() 创建套接字bind() 绑定本机地址和端口connect() …...

Vue+element-ui,实现表格渲染缩略图,鼠标悬浮缩略图放大,点击缩略图播放视频(一)
Vueelement-ui,实现表格渲染缩略图,鼠标悬浮缩略图放大,点击缩略图播放视频 前言整体代码预览图具体分析基础结构主要标签作用videoel-popover 前言 如标题,需要实现这样的业务 此处文章所实现的,是静态视频资源。 注…...
day13 leetcode-hot100-22(链表1)
160. 相交链表 - 力扣(LeetCode) 1.哈希集合HashSet 思路 (1)将A链的所有数据存储到HashSet中。 (2)遍历B链,找到是否在A中存在。 具体代码 /*** Definition for singly-linked list.* pu…...

【Oracle】DQL语言
个人主页:Guiat 归属专栏:Oracle 文章目录 1. DQL概述1.1 什么是DQL?1.2 DQL的核心功能 2. SELECT语句基础2.1 基本语法结构2.2 最简单的查询2.3 DISTINCT去重 3. WHERE条件筛选3.1 基本条件运算符3.2 逻辑运算符组合3.3 高级条件筛选 4. 排序…...

HUAWEI华为MateBook D 14 2021款i5,i7集显非触屏(NBD-WXX9,NbD-WFH9)原装出厂Win10系统
适用型号:NbD-WFH9、NbD-WFE9A、NbD-WDH9B、NbD-WFE9、 链接:https://pan.baidu.com/s/1qTCbaQQa8xqLR-4Ooe3ytg?pwdvr7t 提取码:vr7t 华为原厂WIN系统自带所有驱动、出厂主题壁纸、系统属性联机支持标志、系统属性专属LOGO标志、Office…...

【STIP】安全Transformer推理协议
Secure Transformer Inference Protocol 论文地址:https://arxiv.org/abs/2312.00025 摘要 模型参数和用户数据的安全性对于基于 Transformer 的服务(例如 ChatGPT)至关重要。虽然最近在安全两方协议方面取得的进步成功地解决了服务 Transf…...

leetcode hot100刷题日记——27.对称二叉树
方法一:递归法 class Solution { public:bool check(TreeNode *left,TreeNode *right){//左子树和右子树的节点同时是空的是对称的if(leftnullptr&&rightnullptr){return true;}if(leftnullptr||rightnullptr){return false;}//检查左右子树的值相不相等&a…...

高考加油(Python+HTML)
前言 询问DeepSeek根据自己所学到的知识来生成多个可执行的代码,为高考学子加油。最开始生成的都会有点小问题,还是需要自己调试一遍,下面就是完整的代码,当然了最后几天也不会有多少人看,都在专心的备考。 Python励…...

贪心算法应用:Ford-Fulkerson最大流问题详解
Java中的贪心算法应用:Ford-Fulkerson最大流问题详解 1. 最大流问题概述 最大流问题(Maximum Flow Problem)是图论中的一个经典问题,旨在找到一个从源节点(source)到汇节点(sink)的最大流量。Ford-Fulkerson方法是解决最大流问题的经典算法之一,它属于贪心算法的范畴…...

UE5 Niagara 如何让四元数进行旋转
Axis Angle中,X,Y,Z分别为旋转的轴向,W为旋转的角度,在这里旋转角度不需要除以2,因为里面已经除了,再将计算好的四元数与要进行旋转的四元数进行相乘,结果就是按照原来的角度绕着某一轴向旋转了某一角度...

从“黑箱”到透明化:MES如何重构生产执行全流程?
引言 在传统制造企业中,生产执行环节常面临“计划混乱、进度难控、异常频发、数据滞后”的困境。人工派工效率低下、物料错配频发、质量追溯困难等问题,直接导致交付延期、成本攀升、客户流失。深蓝易网MES系统以全流程数字化管理为核心,通过…...

探索Linux互斥:线程安全与资源共享
个人主页:chian-ocean 文章专栏-Linux 前言: 互斥是并发编程中避免竞争条件和保护共享资源的核心技术。通过使用锁或信号量等机制,能够确保多线程或多进程环境下对共享资源的安全访问,避免数据不一致、死锁等问题。 竞争条件 竞…...

JWT安全:假密钥.【签名随便写实现越权绕过.】
JWT安全:假密钥【签名随便写实现越权绕过.】 JSON Web 令牌 (JWT)是一种在系统之间发送加密签名 JSON 数据的标准化格式。理论上,它们可以包含任何类型的数据,但最常用于在身份验证、会话处理和访问控制机制中发送有关用户的信息(“声明”)。…...
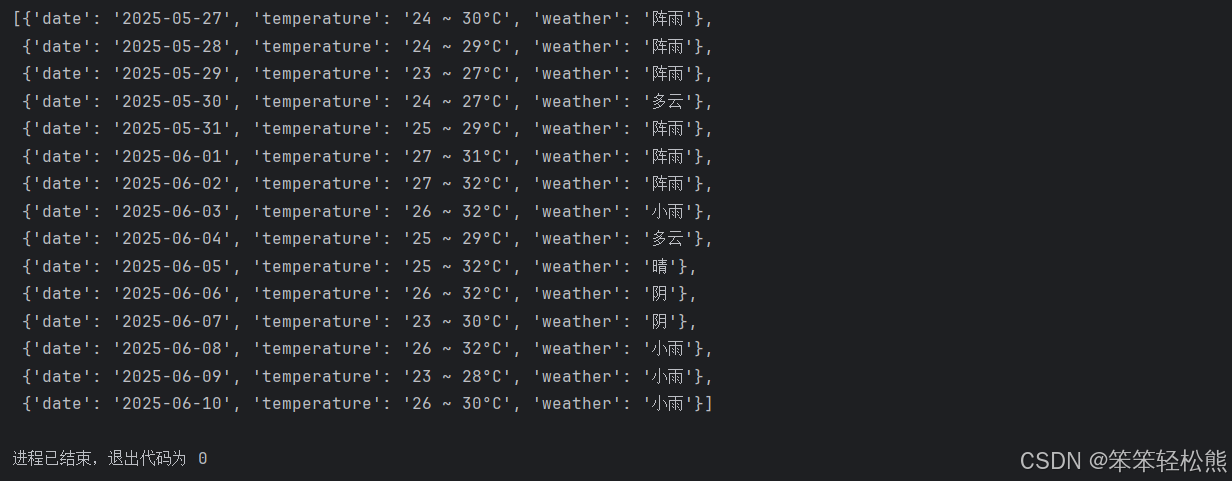
Python爬虫实战:抓取百度15天天气预报数据
🌐 编程基础第一期《9-30》–使用python中的第三方模块requests,和三个内置模块(re、json、pprint),实现百度地图的近15天天气信息抓取 记得安装 pip install requests📑 项目介绍 网络爬虫是Python最受欢迎的应用场景之一&…...

RV1126 + FFPEG多路码流项目
代码主体思路: 一.VI,VENC,RGA模块初始化 1.先创建一个自定义公共结构体,用于方便管理各个模块 rkmedia_config_public.h //文件名字#ifndef _RV1126_PUBLIC_H #define _RV1126_PUBLIC_H#include <assert.h> #include <fcntl.h> #include …...

NodeJS 基于 Koa, 开发一个读取文件,并返回给客户端文件下载,以及读取文件形成列表和文件删除的代码演示
前言 在上一篇文章 《Nodejs 实现 Mysql 数据库的全量备份的代码演示》 中,我们演示了如何将用户的 Mysql 数据库进行备份的代码。但是,这个备份,只是备份在了服务器上了。 而我们用户的真实需求,是需要将备份文件下载到本地进行…...

为什么在我的Flask里面有两个路由,但是在网页里有一个却不能正确访问到智能体
1. /zhoushibo 能访问,/chat 直接浏览器访问报 Method Not Allowed 原因: /zhoushibo 路由是你用 app.route(/zhoushibo) 定义的,返回的是一个HTML网页,浏览器访问没问题。 /chat 路由你用的是 app.route(/chat, methods[POST])…...

哈工大计算机系统2024大作业——Hello的程序人生
计算机系统 大作业 题 目 程序人生-Hello’s P2P 专 业 人工智能 学 号 2022112040 班 级 2203601 学 生 郄东昕 指 导 教 师 吴锐 计算机科学与技术学院…...
2025年软件测试面试八股文(含答案+文档)
🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 Part1 1、你的测试职业发展是什么? 测试经验越多,测试能力越高。所以我的职业发展是需要时间积累的,一步步向着高级测试工程师…...

【仿生系统】qwen的仿生机器人解决方案
收到完整需求后,我将从系统架构设计、算法实现路径、训练方法三个维度为您构建完整的仿生机器人解决方案。以下是分阶段实施方案: 一、核心系统架构设计(模块化可进化架构) 1. 多模态感知引擎 - 视觉子系统:YOLOv8SAM…...

Flutter3.22适配运行鸿蒙系统问题记录
Flutter3.22适配运行鸿蒙系统问题记录 一:适配条件适配过程问题记录(1)环境配置问题(2)Concurrent modification during iteration: Instance(length:2) of_GrowableList 报错(3)三方插件寻找替…...

秋招Day10 - JVM - 内存管理
JVM组织架构主要有三个部分:类加载器、运行时数据区和字节码执行引擎 类加载器:负责从文件系统、网络或其他来源加载class文件,将class文件中的二进制数据加载到内存中运行时数据区:运行时的数据存放的区域,分为方法区…...

Spring Boot 3.5.0中文文档上线
Spring Boot 3.5.0 中文文档翻译完成,需要的可收藏 传送门:Spring Boot 3.5.0 中文文档...
