代码随想录第43天:图论4(最小生成树、拓扑排序)
一、冗余的边II(Kamacoder 109)


from collections import defaultdict# 并查集 - 查找根节点(路径压缩)
def find(fa, x):if fa[x] != x:fa[x] = find(fa, fa[x])return fa[x]# 并查集 - 合并两个集合,返回是否合并成功
def union(fa, x, y):fx, fy = find(fa, x), find(fa, y)if fx != fy:fa[fx] = fyreturn True # 合并成功,无环return False # 已在一个集合中,成环# 判断删除某一条边后,是否构成有向树(无环)
def is_tree_after_removal(edges, remove_idx, n):fa = list(range(n + 1)) # 初始化并查集for i, (u, v) in enumerate(edges):if i == remove_idx: # 跳过指定要删除的边continueif not union(fa, u, v): # 出现环return Falsereturn True# 主函数:找出多余的那条边
def find_redundant_directed_connection(n, edges):in_deg = defaultdict(list) # 记录每个节点的入边索引(用于找入度为2的点)for i, (u, v) in enumerate(edges):in_deg[v].append(i)# 情况 1:存在某个点入度为 2(有两个父节点)for v in in_deg:if len(in_deg[v]) == 2:i1, i2 = in_deg[v]# 优先删除后添加的边(尝试是否能变成树)if is_tree_after_removal(edges, i2, n):return edges[i2]# 否则只能删另一条return edges[i1]# 情况 2:无入度为2的点,仅存在有向环fa = list(range(n + 1)) # 初始化并查集for u, v in edges:if not union(fa, u, v): # 出现环return [u, v]# 读取输入和输出结果
if __name__ == "__main__":n = int(input()) # 节点数edges = [list(map(int, input().split())) for _ in range(n)] # 读取边print(*find_redundant_directed_connection(n, edges)) # 输出多余的那条边
二、寻宝(Kamacoder 53)


最小生成树:在无向图中求一棵树(n-1条边,无环,连通所有点),而且这棵树的边权和最小。
等价于:怎么花最小成本连通无向图的所有点???
Prim(普里姆算法):更适合稠密图,与边的数量没关系,加点法
Kruskal(克鲁斯卡尔算法):更适合稀疏图,与节点的数量没关系,加边法
最小生成树可能不唯一,但是边权和唯一!!!!
# 接收输入:v 个顶点,e 条边
v, e = list(map(int, input().strip().split()))# 使用邻接矩阵初始化图:默认所有节点之间不可达,设为一个很大的数(10001)
graph = [[10001] * (v + 1) for _ in range(v + 1)]
for _ in range(e):x, y, w = list(map(int, input().strip().split()))graph[x][y] = wgraph[y][x] = w # 因为是无向图,双向赋值# 初始化 Prim 算法所需变量
visited = [False] * (v + 1) # 标记哪些节点已加入生成树
minDist = [10001] * (v + 1) # 记录每个节点与当前生成树的最短连接边权重# 从第一个节点开始构建 MST(通常默认从顶点1开始)
minDist[1] = 0 # 起点到自己权重为 0# Prim 主循环:重复选择 v 次,每次选择一个未加入树的、距离最小的节点
for _ in range(1, v + 1):min_val = 10002 # 当前最小权重(初始为无穷大)cur = -1 # 当前选择加入树的节点# 遍历所有未访问的节点,选出与树连接距离最小的那个for j in range(1, v + 1):if not visited[j] and minDist[j] < min_val:cur = jmin_val = minDist[j]visited[cur] = True # 标记该节点已加入 MST# 更新其他未加入节点的 minDist,如果通过新加入的 cur 更近for j in range(1, v + 1):if not visited[j] and graph[cur][j] < minDist[j]:minDist[j] = graph[cur][j]# 累加所有边权(minDist[1] 是起点设为 0,可以忽略)
ans = sum(minDist[2:]) # minDist[1] 为起点设为 0,不计入答案
print(ans)
三、软件构建(Kamacoder 117)


拓扑排序:所有点按照先后顺序排成序列,每次选入度为0的点,然后删除这个点和它的出边,如果拓扑排序进行不下去了,说明图中有环。
from collections import deque, defaultdictdef topo_sort(n, edges):indeg = [0] * n # indeg[i] 表示点 i 的入度(被多少个点指向)graph = defaultdict(list) # 用邻接表 graph 存储有向图,graph[u] 里是所有从 u 出发可达的点# 构建图和入度数组for u, v in edges:graph[u].append(v) # u 指向 vindeg[v] += 1 # v 的入度加一# 将所有入度为 0 的点入队,表示它们可以首先被处理q = deque(i for i in range(n) if indeg[i] == 0)res = [] # 存储拓扑排序的结果while q:u = q.popleft() # 取出一个入度为 0 的点res.append(u) # 加入结果中for v in graph[u]: # 遍历 u 指向的所有节点indeg[v] -= 1 # u 被处理了,v 的入度减一if indeg[v] == 0: # 若 v 入度减为 0,加入队列等待处理q.append(v)# 若结果中包含了所有 n 个节点,说明成功排序;否则图中有环,无法拓扑排序print(" ".join(map(str, res)) if len(res) == n else -1)if __name__ == "__main__":# 读取顶点数 n 和边数 mn, m = map(int, input().split())# 读取 m 条边,构建边列表edges = [tuple(map(int, input().split())) for _ in range(m)]# 调用拓扑排序函数topo_sort(n, edges)
相关文章:

代码随想录第43天:图论4(最小生成树、拓扑排序)
一、冗余的边II(Kamacoder 109) from collections import defaultdict# 并查集 - 查找根节点(路径压缩) def find(fa, x):if fa[x] ! x:fa[x] find(fa, fa[x])return fa[x]# 并查集 - 合并两个集合,返回是否合并成功 …...

AI智能体|扣子(Coze)搭建【自动生成超高质量PPT】工作流
各位好久不见,你的失踪人口又回来了,已经超过一周的时间没有进行文章的更新了。 没更新的这段时间,主要还是因为工作上的调整以及身体生病所导致的停更,具体以后再说。 我们先讲今天的主要主题,使用 Coze 智能体一键生…...
的两个问题)
list.sort(*, key=None, reverse=False)的两个问题
在python官网中,5.1. More on Lists,list.sort()是关于排序的方法。 list.sort(*, keyNone, reverseFalse) 中有两个问题: * 是什么意思key有什么作用 * 是什么意思 * 表示后面必须是关键字参数,具体见python官网4…...

文档处理的相关工具
目前网页端的文档,可以通过沉浸式翻译来进行翻译阅读和学习。 但是某些文献只有pdf下载的版本,所以需要一个免费的针对pdf的翻译工具。 保留公式和图片格式。 推荐一个pdf翻译的工具,可以自己部署使用。如果需要word版本,后面讨论…...

java基础(面向对象进阶高级)内部类
内部类 内部类概述、成员内部类 (了解) 内部类创建对象: 一定要继承外部类对象,才能创建内部类对象。 拓展:成员内部类访问外部类的成员特点: 成员内部类中,是否可以直接访问外部类的实例成员?? 当然可以啊&#x…...

使用Python,OpenCV,Tesseract-OCR对自己的运动数据图片进行识别及分析,并使用Matplotlib绘制配速图出来
使用Python,OpenCV,Tesseract-OCR对自己的运动数据图片进行识别及分析,并使用Matplotlib绘制配速图出来 1. 效果图2. 源码3. 全量源码及运动图片资源参考主要分为 目录下图片解析及读取;拼九宫格图片出来,可以自由配置(m*n)取决于自己有多少张运动图片遍历图片并进行运动…...

小白的进阶之路系列之七----人工智能从初步到精通pytorch自动微分优化以及载入和保存模型
本文将介绍Pytorch的以下内容 自动微分函数 优化 模型保存和载入 好了,我们首先介绍一下关于微分的内容。 在训练神经网络时,最常用的算法是反向传播算法。在该算法中,根据损失函数相对于给定参数的梯度来调整参数(模型权重)。 为了计算这些梯度,PyTorch有一个内置…...

创建型模式之 Builder (生成器)
创建型模式之 Builder (生成器) 摘要: 本文介绍了生成器(Builder)设计模式,属于创建型模式之一。该模式通过将复杂对象的构建与表示分离,使同一构建过程能创建不同表现形式。文章以小米汽车不同配置版本为例说明了模式…...

智能物资出入库管控系统
概述 智能物资管理系统利用RFID自动识别技术,物联网技术、人脸识别、指纹、指静脉生物识别技术,应用于军械装备的管理,可实时准确采集军械装备编配、 储存、供应、使用等数据,实时掌握军械装备物资的分布及数量 状况。细化管理到…...

鸿蒙OSUniApp 制作倒计时与提醒功能#三方框架 #Uniapp
使用 UniApp 制作倒计时与提醒功能 前言 倒计时与提醒功能在移动应用中应用广泛,如活动秒杀、任务提醒、考试倒计时等。一个实用的倒计时组件不仅要精准计时,还要兼容多端,尤其是在鸿蒙(HarmonyOS)等新兴平台上保证流…...

深入剖析网络协议:七层协议与四层协议详解
在计算机网络的世界中,数据的传输与交互离不开协议的规范。其中,七层协议和四层协议是网络通信架构的核心概念,它们如同网络世界的 “交通规则”,保障着数据准确、高效地在不同设备间流转。本文将深入解读七层协议与四层协议&…...

机器学习-线性回归基础
一、什么是回归 依据输入x写出一个目标值y的计算方程,求回归系数的过程就叫回归。简言之:根据题意列出方程,求出系数的过程就叫做回归。 回归的目的是预测数值型的目标值y,分类的目的预测标称型的目标值y。 二、线性回归 2.1线性…...

自学嵌入式 day 25 - 系统编程 标准io 缓冲区 文件io
(3)二进制文件读写函数: ①fread: size_t fread(void *ptr, size_t size, size_t nmemb, FILE *stream); 功能:从指定的stream流对象中获取nmemeb个大小为size字节的数据块到ptr所在的本地内存中。 参数&…...
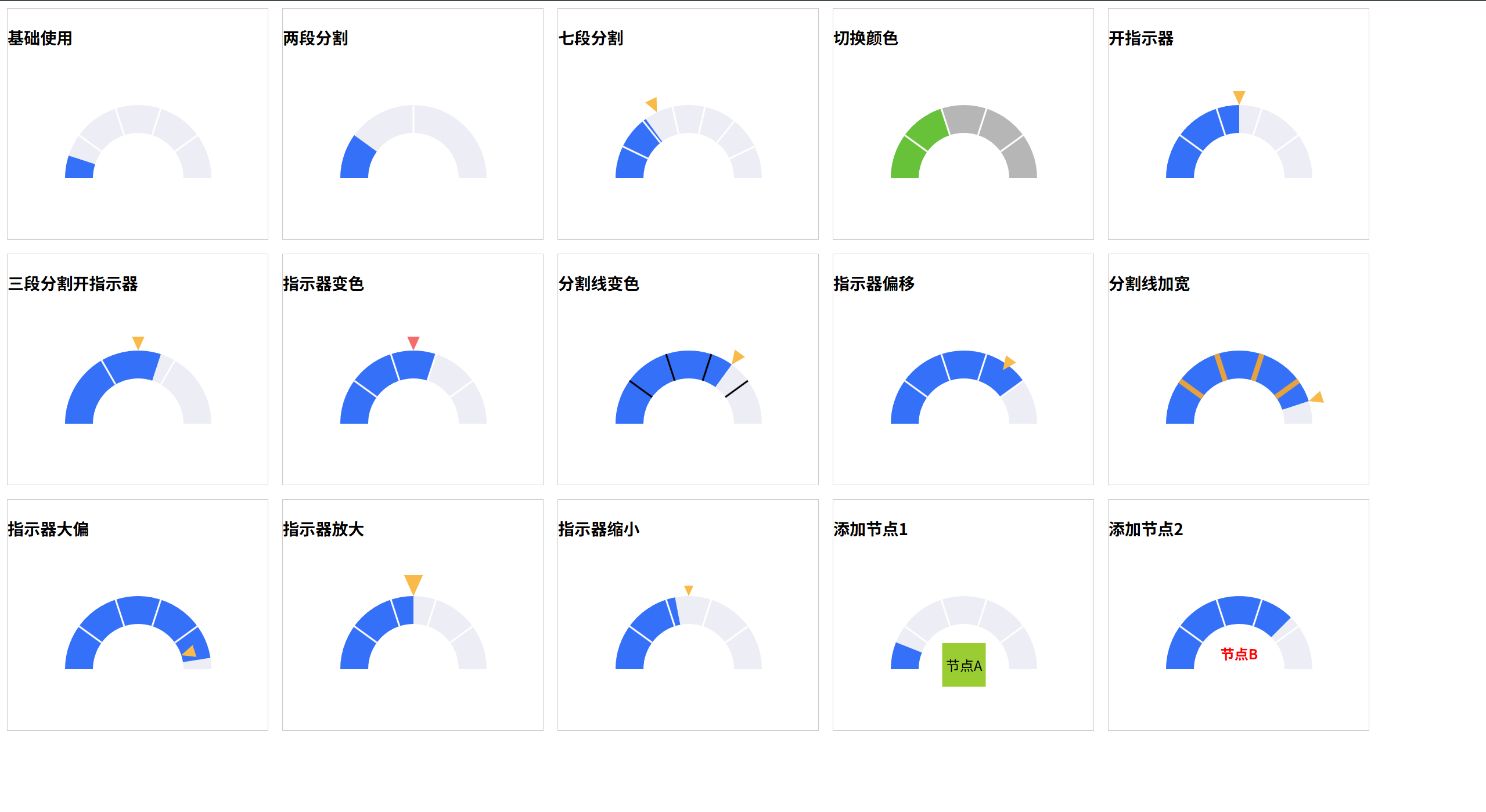
[Vue组件]半环进度显示器
[Vue组件]半环进度显示器 纯svg实现,不需要其他第三方库,功能简单,理论上现代浏览器都能支持 封装组件 所有参数都选填,进度都可选填 <template><div class"ys-semiring"><div class"svg-container…...

科技赋能建筑行业,智能楼宇自控系统崭露头角成发展新势力
在科技浪潮席卷全球的时代背景下,传统建筑行业正面临着前所未有的变革压力。随着城市化进程加快,建筑规模与复杂度不断攀升,能源消耗、运营效率、用户体验等问题日益凸显。智能楼宇自控系统凭借物联网、大数据、人工智能等前沿技术࿰…...
)
Rust入门之并发编程基础(一)
Rust入门之并发编程基础(一) 无畏并发 本文源码 安全且高效地处理并发编程是 Rust 的另一个主要目标。并发编程(Concurrent programming),代表程序的不同部分相互独立地执行,而 并行编程(par…...
)
高级特性实战:死信队列、延迟队列与优先级队列(二)
三、延迟队列:实现任务定时执行 3.1 延迟队列概念解析 延迟队列(Delay Queue),是一种特殊的队列,它的独特之处在于队列中的元素(消息)并不会立即被处理,而是会在指定的延迟时间过后…...

VR 电缆故障测试系统:技术革新
VR 电缆故障测试系统,作为电力领域的创新科技成果,融合了虚拟现实技术、三维建模、实时交互等前沿技术,为电缆故障测试带来了全新的解决方案。它的工作原理犹如一位经验丰富的侦探,通过层层线索,精准地锁定电缆故障的位…...

Rocky Linux上安装Go
使用官方二进制包安装 1. 下载 Go 官方二进制包 cd /tmp wget https://go.dev/dl/go1.22.3.linux-amd64.tar.gz2. 解压并安装到 /usr/local sudo rm -rf /usr/local/go # 如果之前有旧版本先删除 sudo tar -C /usr/local -xzf go1.22.3.linux-amd64.tar.gz3. 设置环境变量…...

深度学习论文: FastVLM: Efficient Vision Encoding for Vision Language Models
深度学习论文: FastVLM: Efficient Vision Encoding for Vision Language Models FastVLM: Efficient Vision Encoding for Vision Language Models PDF: https://www.arxiv.org/abs/2412.13303 PyTorch代码: https://github.com/shanglianlm0525/CvPytorch PyTorch代码: https…...

白杨SEO:做AI搜索优化的DeepSeek、豆包、Kimi、百度文心一言、腾讯元宝、通义、智谱、天工等AI生成内容信息采集主要来自哪?占比是多少?
大家好,我是白杨SEO,专注SEO十年以上,全网SEO流量实战派,AI搜索优化研究者。 在开始写之前,先说个抱歉。 上周在上海客户以及线下聚会AI搜索优化分享说各大AI模型的联网搜索是关闭的,最开始上来确实是的。…...

显示docker桌面,vnc远程连接docker
目录 相关概念: 实现步骤: 1.启动docker容器 2.安装x11 3.Docker 容器中安装一个完整的图形桌面(XFCE)和 VNC 远程桌面服务器(TightVNC) 4.配置vncservice 5.本地安装VNC Viewer连接VNC Viewer下载地…...

Web 端顶级视效实现:山海鲸端渲染底层原理与发布模式详解
大家好,欢迎大家回到山海鲸的渲染模式系列教程。昨天,我们看了一下山海鲸支持的3种渲染模式的整体概览。今天,我们就来看一下山海鲸支持的最基础的渲染模式,也就是端渲染的渲染设置。 1. 山海鲸的端渲染 我们说到端渲染…...

腾讯云国际站性能调优
全球化业务扩张中,云端性能直接决定用户体验与商业成败。腾讯云国际站通过资源适配、网络优化与存储革新,为企业提供全链路调优方案。 资源精准适配 实例选型需与业务场景深度耦合,计算优化型实例加速AI训练效率3倍,内存…...

深入解析操作系统内核与用户空间以及内核态与用户态转换
用户空间和内核空间的划分是现代操作系统的基础,对应用程序网络模型的设计和优化有着深远的影响。 内核空间与用户空间的分工 现代操作系统为了保证系统的稳定性和安全性,将虚拟内存空间划分为用户空间和内核空间。 一、用户空间 用户空间是用户程序…...

每日一题洛谷P8662 [蓝桥杯 2018 省 AB] 全球变暖c++
P8662 [蓝桥杯 2018 省 AB] 全球变暖 - 洛谷 (luogu.com.cn) DFS #include<iostream> using namespace std; int n, res; char a[1005][1005]; bool vis[1005][1005]; bool flag; int dx[4] { 0,0,1,-1 }; int dy[4] { 1,-1,0,0 }; void dfs(int x, int y) {vis[x][y]…...
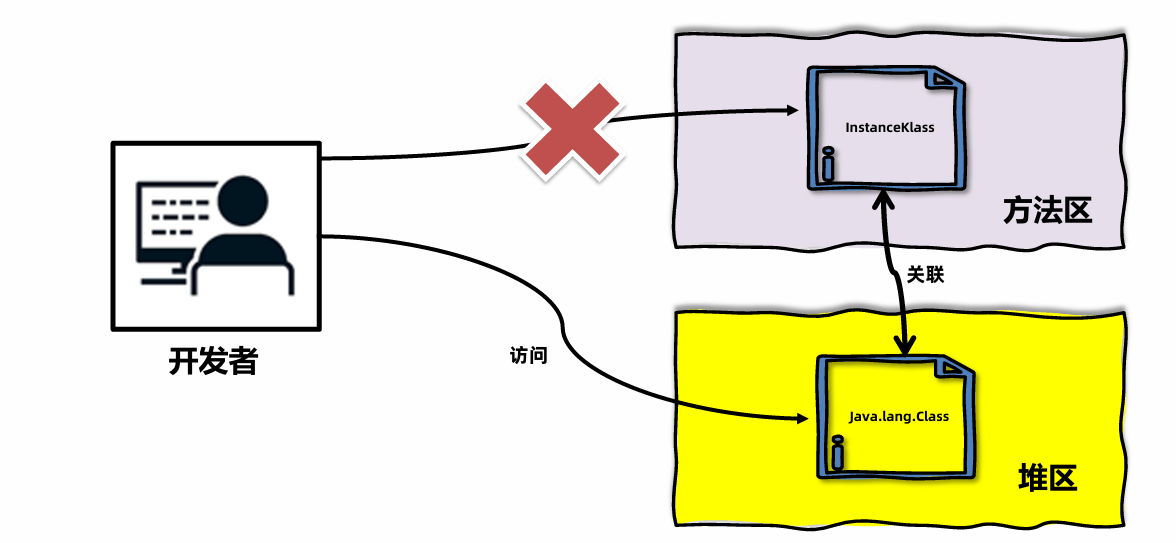
【JVM】初识JVM 从字节码文件到类的生命周期
初识JVM JVM(Java Virtual Machine)即 Java 虚拟机,是 Java 技术的核心组件之一。JVM的本质就是运行在计算机上的一个程序,通过软件模拟实现了一台抽象的计算机的功能。JVM是Java程序的运行环境,负责加载字节码文件&a…...

多级体验体系构建:基于开源AI智能客服与AI智能名片的S2B2C商城小程序体验升级路径研究
摘要:在体验经济时代,传统企业单一的总部体验模式难以覆盖全链路用户需求。本文针对B端与C端体验深度差异,提出“一级总部体验—二级区域体验—三级终端体验”的分层架构,并引入“开源AI智能客服”与“AI智能名片”技术࿰…...

每日算法 -【Swift 算法】字符串转整数算法题详解:myAtoi 实现与正则表达式对比
Swift 字符串转整数算法题详解:myAtoi 实现与正则表达式对比 🧩 题目背景 LeetCode 上的经典算法题 8. String to Integer (atoi) 是一道考察字符串解析与边界处理的题目。这道题虽看似简单,但处理细节相当复杂。我们将使用 Swift 语言实现…...

记录一个难崩的bug
1.后端配置了 Filter 过滤器,如果再配置了Configuration ,那么会出现冲突吗? 过滤器与Configuration类本身无直接冲突,但需注意注册机制、执行顺序和依赖管理。通过显式控制过滤器的注册方式和优先级,结合Spring Security的链式配…...
