PyTorch 中mm和bmm函数的使用详解
torch.mm 是 PyTorch 中用于 二维矩阵乘法(matrix-matrix multiplication) 的函数,等价于数学中的 A × B 矩阵乘积。
一、函数定义
torch.mm(input, mat2) → Tensor
执行的是两个 2D Tensor(矩阵)的标准矩阵乘法。
input: 第一个二维张量,形状为(n × m)mat2: 第二个二维张量,形状为(m × p)- 返回:形状为
(n × p)的张量
二、使用条件和注意事项
| 条件 | 说明 |
|---|---|
| 仅支持 2D 张量 | 一维或三维以上使用 torch.matmul 或 @ 操作符 |
| 维度要匹配 | 即 input.shape[1] == mat2.shape[0] |
| 不支持广播 | 两个矩阵维度不匹配会直接报错 |
| 结果是普通矩阵乘积 | 不是逐元素乘法(Hadamard),即不是 * 或 torch.mul() |
三、示例代码
示例 1:基本矩阵乘法
import torchA = torch.tensor([[1., 2.], [3., 4.]]) # 2x2
B = torch.tensor([[5., 6.], [7., 8.]]) # 2x2C = torch.mm(A, B)
print(C)
输出:
tensor([[19., 22.],[43., 50.]])
计算步骤:
C[0][0] = 1*5 + 2*7 = 19
C[0][1] = 1*6 + 2*8 = 22
...
示例 2:不匹配维度导致报错
A = torch.rand(2, 3)
B = torch.rand(4, 2)
C = torch.mm(A, B) # ❌ 会报错
报错:
RuntimeError: mat1 and mat2 shapes cannot be multiplied (2x3 and 4x2)
示例 3:推荐写法(推荐使用 @ 或 matmul)
A = torch.rand(3, 4)
B = torch.rand(4, 5)C1 = torch.mm(A, B)
C2 = A @ B # 推荐用法
C3 = torch.matmul(A, B) # 推荐用法
四、与其他乘法函数的比较
| 函数名 | 支持维度 | 运算类型 | 支持广播 |
|---|---|---|---|
torch.mm | 仅限二维 | 矩阵乘法 | ❌ 不支持 |
torch.matmul | 1D, 2D, ND | 自动判断点乘 / 矩阵乘 | ✅ 支持 |
torch.bmm | 批量二维乘法 | 3D Tensor batch × batch | ❌ 不支持 |
torch.mul | 任意维度 | 元素乘(Hadamard) | ✅ 支持 |
* 运算符 | 任意维度 | 元素乘 | ✅ 支持 |
@ 运算符 | ND(推荐用) | 矩阵乘法(和 matmul 一样) | ✅ |
五、典型应用场景
- 神经网络权重乘法:
output = torch.mm(W, x) - 点云 / 图像变换:
x' = torch.mm(R, x) + t - 多层感知机中的矩阵计算
- 注意力机制中 QK^T 乘积
六、总结:什么时候用 mm?
| 使用场景 | 用什么 |
|---|---|
| 仅二维矩阵乘法 | torch.mm |
| 高维或支持广播乘法 | torch.matmul / @ |
| 批量矩阵乘法 (如 batch_size×3×3) | torch.bmm |
| 元素乘 | torch.mul or * |
在 PyTorch 中,torch.bmm 是 批量矩阵乘法(batch matrix multiplication) 的操作,专用于处理三维张量(batch of matrices)。它的主要作用是对一组矩阵成对进行乘法,效率远高于手动循环计算。
一、torch.bmm 语法
torch.bmm(input, mat2, *, out=None) → Tensor
- input:
Tensor,形状为(B, N, M) - mat2:
Tensor,形状为(B, M, P) - 返回结果形状为
(B, N, P)
这表示对 B 对 N×M 和 M×P 的矩阵进行成对相乘。
二、示例演示
示例 1:基础用法
import torch# 定义两个 batch 矩阵
A = torch.randn(4, 2, 3) # shape: (B=4, N=2, M=3)
B = torch.randn(4, 3, 5) # shape: (B=4, M=3, P=5)# 批量矩阵乘法
C = torch.bmm(A, B) # shape: (4, 2, 5)print(C.shape) # 输出: torch.Size([4, 2, 5])
示例 2:手动循环 vs bmm 效率对比
# 慢速手动方式
C_manual = torch.stack([A[i] @ B[i] for i in range(A.size(0))])# 等效于 bmm
C_bmm = torch.bmm(A, B)print(torch.allclose(C_manual, C_bmm)) # True
三、注意事项
1. 维度必须是三维张量
- 否则会报错:
RuntimeError: batch1 must be a 3D tensor
你可以通过 .unsqueeze() 手动调整维度:
a = torch.randn(2, 3)
b = torch.randn(3, 4)# 升维
a_batch = a.unsqueeze(0) # (1, 2, 3)
b_batch = b.unsqueeze(0) # (1, 3, 4)c = torch.bmm(a_batch, b_batch) # (1, 2, 4)
2. 维度必须满足矩阵乘法规则
(B, N, M)×(B, M, P)→(B, N, P)- 若
M不一致会报错:
RuntimeError: Expected size for the second dimension of batch2 tensor to match the first dimension of batch1 tensor
3. bmm 不支持广播(broadcasting)
- 必须显式提供相同的 batch size。
- 如果只有一个矩阵固定,可以使用
.expand():
A = torch.randn(1, 2, 3) # 单个矩阵
B = torch.randn(4, 3, 5) # 4 个矩阵# 扩展 A 以进行 batch 乘法
A_expand = A.expand(4, -1, -1)
C = torch.bmm(A_expand, B) # (4, 2, 5)
四、在实际应用中的例子
在点云变换中:批量乘旋转矩阵
# 假设有 B 个旋转矩阵和点坐标
R = torch.randn(B, 3, 3) # 旋转矩阵
points = torch.randn(B, 3, N) # 点云# 先转置点坐标为 (B, N, 3)
points_T = points.transpose(1, 2) # (B, N, 3)# 用 bmm 做点变换:每组点乘旋转
transformed = torch.bmm(points_T, R.transpose(1, 2)) # (B, N, 3)
五、总结
| 特性 | torch.bmm |
|---|---|
| 操作对象 | 三维张量(batch of matrices) |
| 核心规则 | (B, N, M) x (B, M, P) = (B, N, P) |
| 是否支持广播 | ❌ 不支持,需要手动 .expand() |
与 matmul 区别 | matmul 支持更多广播,bmm 更高效用于纯批量矩阵乘法 |
| 应用场景 | 批量线性变换、点云配准、神经网络前向传播等 |
相关文章:

PyTorch 中mm和bmm函数的使用详解
torch.mm 是 PyTorch 中用于 二维矩阵乘法(matrix-matrix multiplication) 的函数,等价于数学中的 A B 矩阵乘积。 一、函数定义 torch.mm(input, mat2) → Tensor执行的是两个 2D Tensor(矩阵)的标准矩阵乘法。 in…...

关于表连接
目录 1.左连接 2.右连接 3.内连接 4.全外连接 5.笛卡尔积 -- 创建表A CREATE TABLE A(PNO VARCHAR2(10) PRIMARY KEY, PAMT NUMBER, A_DATE DATE);-- 向表A插入数据 INSERT INTO A VALUES (01001, 100, TO_DATE(2005-01-01, YYYY-MM-DD)); INSERT INTO A VALUES (010…...

【计算机网络】fork()+exec()创建新进程(僵尸进程及孤儿进程)
文章目录 一、基本概念1. fork() 系统调用2. exec() 系列函数 二、典型使用场景1. 创建子进程执行新程序2. 父子进程执行不同代码 三、核心区别与注意事项四、组合使用技巧1. 重定向子进程的输入/输出2. 创建多级子进程 五、常见问题与解决方案僵尸进程(Zombie Proc…...

QPS 和 TPS 详解
QPS 和 TPS 是性能测试中的两个核心指标,用于衡量系统的吞吐能力,但关注点不同。以下是具体解析: 1. QPS(Queries Per Second) 定义:每秒查询数,表示系统每秒能处理的请求数量(无论…...

Word表格怎样插入自动序号或编号
在Word文档中编辑表格时,经常需要为表格添加序号或编号,可以设置为自动序号或编号,当删除行时,编号会自动变化,不用手工再重新编号。如图所示。 序号数据1数据21300300230030033003004300300 一,建立word表…...

数据结构:导论
目录 什么是“第一性原理”? 什么是“数据结构”? 数据结构解决的根本问题是什么? 数据结构的两大分类 数据结构的基本操作 数据结构与算法的关系 学习数据结构的底层目标 什么是“第一性原理”? 在正式进入数据结构之前&…...

青少年编程与数学 02-020 C#程序设计基础 13课题、数据访问
青少年编程与数学 02-020 C#程序设计基础 13课题、数据访问 一、使用数据库1. 使用ADO.NET连接数据库连接SQL Server示例连接其他数据库 2. 使用Entity Framework (EF Core)安装EF Core示例代码 3. 数据绑定到WinForms控件DataGridView绑定简单控件绑定 4. 使用本地数据库(SQLi…...

无人机仿真环境(3维)附项目git链接
项目概述 随着无人机技术在物流、测绘、应急救援等领域的广泛应用,其自主导航、避障算法、路径规划及多机协同等核心技术的研究需求日益迫切。为降低实地测试成本、提高研发效率,本项目旨在构建一个高精度、可扩展的无人机三维虚拟仿真环境&…...

湖北理元理律师事务所:债务优化中的“生活锚点”设计
在债务重组领域,一个常被忽视的核心矛盾是:还款能力与生存需求的冲突。过度压缩生活支出还债,可能导致收入中断;放任债务膨胀,又加剧精神压力。湖北理元理律师事务所通过“三步平衡法”,尝试在法理框架内破…...
Python 训练营打卡 Day 30-模块和库的导入
模块和库的导入 1.1标准导入 import mathprint("方式1: 使用 import math") print(f"圆周率π的值: {math.pi}") print(f"2的平方根: {math.sqrt(2)}\n") 1.2从库中导入特定项 from math import pi, sqrtprint("方式2:使用 f…...

前端实现图片压缩:基于 HTML5 File API 与 Canvas 的完整方案
在 Web 开发中,处理用户上传的图片时,前端压缩可以有效减少服务器压力并提升上传效率。本文将详细讲解如何通过<input type="file">实现图片上传,结合 Canvas 实现图片压缩,并实时展示压缩前后的图片预览和文件大小对比。 一、核心功能架构 我们将实现以…...

【Docker管理工具】部署Docker管理面板DweebUI
【Docker管理工具】部署Docker管理面板DweebUI 一、DweebUI介绍1.1 DweebUI 简介1.2 主要特点1.3 使用场景 二、本次实践规划2.1 本地环境规划2.2 本次实践介绍 三、本地环境检查3.1 检查Docker服务状态3.2 检查Docker版本3.3 检查docker compose 版本 四、下载DweebUI镜像五、…...

【后端高阶面经:架构篇】50、数据存储架构:如何改善系统的数据存储能力?
一、数据存储架构设计核心原则 (一)分层存储架构:让数据各得其所 根据数据访问频率和价值,将数据划分为热、温、冷三层,匹配不同存储介质,实现性能与成本的平衡。 热数据层:访问频率>100次/秒。采用Redis集群存储高频访问数据(如用户登录态、实时交易数据),配合…...

编程之巅:语言的较量
第一章:代码之城的召集令 在遥远的数字大陆上,有一座名为“代码之城”的神秘都市。这里居住着各种编程语言的化身,他们以拟人化的形态生活,每种语言都有独特的性格与技能。Python是个优雅的学者,C是个硬核战士&#x…...

STM32 通过 ESP8266 通信详解
✅作者简介:热爱科研的嵌入式开发者,修心和技术同步精进 ❤欢迎关注我的知乎:对error视而不见 代码获取、问题探讨及文章转载可私信。 ☁ 愿你的生命中有够多的云翳,来造就一个美丽的黄昏。 🍎获取更多嵌入式资料可点击链接进群领…...

Qt/C++开发监控GB28181系统/sip协议/同时支持udp和tcp模式/底层协议解析
一、前言说明 在gb28181-2011协议中,只有udp要求,从2016版本开始要求支持tcp,估计也是在多年的实际运行过程中,发现有些网络环境差的场景下,一些udp交互指令丢失导致功能异常,所以后面修订的时候增加了tcp…...
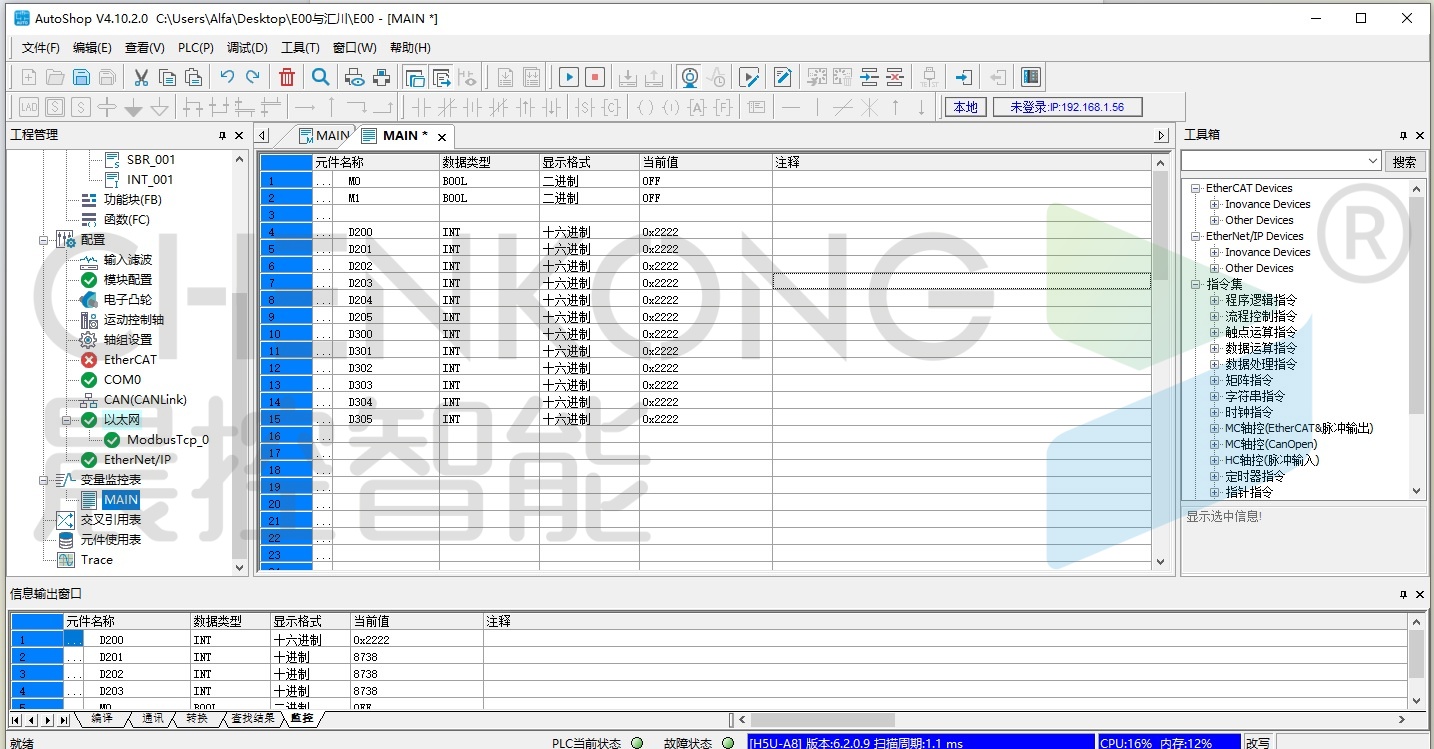
晨控CK-FR03与汇川H5U系列PLC配置MODBUS TCP通讯连接操作手册
晨控CK-FR03与汇川H5U系列PLC配置MODBUS TCP通讯连接操作手册 CK-FR03-TCP是一款基于射频识别技术的高频RFID标签读卡器,读卡器工作频率为13.56MHZ,支持对I-CODE 2、I-CODE SLI等符合ISO15693国际标准协议格式标签的读取。 读卡器同时支持标准工业通讯协…...

山海鲸轻 3D 渲染技术深度解析:预渲染如何突破多终端性能瓶颈
在前期课程中,我们已系统讲解了山海鲸两大核心渲染模式——云渲染与端渲染的技术特性及配置方法。为满足复杂场景下的差异化需求,山海鲸创新推出轻3D渲染功能,本文将深度解析该技术的实现原理与操作实践。 一、轻3D功能研发背景 针对多终端协…...

t014-项目申报管理系统 【springBoot 含源码】
项目演示视频 摘 要 传统信息的管理大部分依赖于管理人员的手工登记与管理,然而,随着近些年信息技术的迅猛发展,让许多比较老套的信息管理模式进行了更新迭代,项目信息因为其管理内容繁杂,管理数量繁多导致手工进行…...

阻止H5页面中键盘收起的问题
在移动端H5开发中,当输入框失去焦点时,键盘会自动收起,但有时我们需要阻止这种行为。以下是几种解决方案: 常见原因 输入框失去焦点触发键盘收起页面滚动或触摸其他区域导致键盘收起某些浏览器(特别是iOS Safari)的默认行为 解…...

将 AI 解答转换为 Word 文档
相关说明 DeepSeek 风靡全球的2025年,估计好多人都已经试过了,对于理科老师而言,有一个使用痛点,就是如何将 AI 输出的 mathjax 格式的符号转化为我们经常使用的 mathtype 格式的,以下举例说明。 温馨提示࿱…...

AI 产品的 MVP 构建逻辑:Prompt 工程 ≠ 产品工程?
一、引言:技术细节与系统工程的本质分野 在 AI 产品开发的战场中,Prompt 工程与产品工程的边界模糊正在引发深刻的认知革命。当工程师们沉迷于优化 “请用三段式结构分析用户需求” 这类提示词时,产品经理却在思考如何通过用户行为数据验证 …...

Go语言开发的GMQT物联网MQTT消息服务器(mqtt Broker)支持海量MQTT连接和快速低延时消息传输-提供源码可二次开发定制需求
关于GMQT物联网MQTT消息平台 GoFly社区推出《GMQT物联网MQTT消息平台》,完全使用高性能的Go语言编写,内嵌数据库(不依赖三方库), 全面支持MQTT的v3.0.0、v3.1.1以及完全兼容 MQTT v5 功能。利用Go语言高并发性、高效利用服务器资源、跨平台支…...
.filter() 链式调用,语法解析 和常见demo)
JavaScript es6 语法 map().filter() 链式调用,语法解析 和常见demo
摘要: map:遍历数组并对每个元素执行回调函数,返回一个新数组 filter:对 map 返回的数组进行过滤,返回满足条件的元素组成的新数组 1.数字数组处理 const numbers [1, 2, 3, 4, 5];// 先平方,再筛选偶数…...

leetcode2221. 数组的三角和-medium
1 题目:数组的三角和 官方标定难度:中 给你一个下标从 0 开始的整数数组 nums ,其中 nums[i] 是 0 到 9 之间(两者都包含)的一个数字。 nums 的 三角和 是执行以下操作以后最后剩下元素的值: nums 初始…...

Express教程【001】:Express创建基本的Web服务器
文章目录 1、初识express1.1 什么是Express1.2 主要特点1.3 Express的基本使用1.3.1 安装1.3.2 创建基本的Web服务器 1、初识express 目标: 能够使用express.static()快速托管静态资源能够使用express路由精简项目结构能够使用常见的express中间件能够使用express创…...

asio之async_result
简介 async_result用来表示异步处理返回类型 async_result 是类模板 type:为类模板中声明的类型,对于不同的类型,可以使用类模板特例化,比如针对use_future...

代码随想录算法训练营 Day60 图论Ⅹ Bellmen_ford 系列算法
图论 题目 94. 城市间货物运输 I Bellmen_ford 队列优化算法 SPFA 大家可以发现 Bellman_ford 算法每次松弛 都是对所有边进行松弛。 但真正有效的松弛,是基于已经计算过的节点在做的松弛。 本图中,对所有边进行松弛,真正有效的松弛&#…...

独立机构软件第三方检测:流程、需求分析及电商软件检验要点?
独立机构承担着对软件进行第三方检测的任务,这一环节对于提升软件的质量和稳定性起到了极其关键的作用。检测过程拥有一套完善的流程,目的在于确保检测结果的精确性,并保障软件达到高标准。 需求分析 确保软件测试需求清晰十分关键。我们需…...

Java构建Tree并实现节点名称模糊查询
乐于学习分享… 大家加油努力 package com.tom.backtrack;import lombok.Data; import lombok.Getter;import java.util.ArrayList; import java.util.List; import java.util.Objects;/*** 树节点** author zx* date 2025-05-27 19:51*/ Data public class TreeNode {private …...
