机器学习中的线性回归:从理论到实践的深度解析
一、引言
线性回归(Linear Regression)是机器学习和统计学中最基础且应用广泛的模型之一,用于预测连续型目标变量。它通过建立输入特征与输出变量之间的线性关系,实现对未知数据的预测。无论是预测房价、股票走势,还是分析广告投入与销售额的关系,线性回归都能提供简洁而有效的解决方案。本文将从理论推导、数学模型、优化算法到实际应用,全面解析线性回归的核心内容。
二、基本概念与数学模型
1. 单变量线性回归
假设我们有一个输入特征 x(如房屋面积)和一个输出变量 y(如房价),单变量线性回归模型可表示为:\(y = \theta_0 + \theta_1 x + \epsilon\) 其中:
- \(\theta_0\)(截距)和 \(\theta_1\)(斜率)是模型参数,需通过数据学习得到。
- \(\epsilon\) 是误差项,服从正态分布 \(\epsilon \sim N(0, \sigma^2)\)。
模型的预测值为:\(\hat{y} = h_\theta(x) = \theta_0 + \theta_1 x\) 目标是找到最优的 \(\theta_0\) 和 \(\theta_1\),使预测值 \(\hat{y}\) 尽可能接近真实值 y。
2. 多变量线性回归
当输入特征有 n 个(如面积、房间数、楼层等),模型扩展为:\(\hat{y} = h_\theta(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \dots + \theta_n x_n\) 用向量形式表示(引入截距项 \(x_0=1\),将参数合并为 \(\theta = [\theta_0, \theta_1, \dots, \theta_n]^T\),输入特征向量 \(x = [x_0, x_1, \dots, x_n]^T\)):\(\hat{y} = \theta^T x\)
三、损失函数与优化目标
1. 均方误差(MSE)损失函数
为衡量预测误差,定义损失函数为 误差平方和的平均值(MSE):\(J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})^2\) 其中 m 是样本数,\((x^{(i)}, y^{(i)})\) 是第 i 个样本。乘以 \(\frac{1}{2}\) 是为了求导时简化计算(不影响最小值点)。
2. 优化目标
通过最小化 \(J(\theta)\) 求解参数 \(\theta\),即:\(\min_\theta J(\theta)\) 由于 \(J(\theta)\) 是关于 \(\theta\) 的凸函数(二阶导数非负),存在唯一全局最小值,可通过 梯度下降 或 正规方程 求解。
四、优化算法:梯度下降
1. 梯度计算
对 \(J(\theta)\) 求偏导(以单变量为例):\(\frac{\partial J}{\partial \theta_0} = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)})\)\(\frac{\partial J}{\partial \theta_1} = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) x^{(i)}\) 多变量时,对每个 \(\theta_j\) 求偏导:\(\frac{\partial J}{\partial \theta_j} = \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)}\)
2. 梯度下降更新规则
\(\theta_j := \theta_j - \alpha \frac{\partial J}{\partial \theta_j}\) 其中 \(\alpha\) 是学习率(控制每步更新幅度)。迭代更新参数,直到收敛(损失函数变化小于阈值)。
3. 梯度下降的变种
- 批量梯度下降(BGD):每次用全量数据计算梯度(稳定但计算量大)。
- 随机梯度下降(SGD):每次用单个样本计算梯度(快但波动大)。
- 小批量梯度下降(MBGD):折中方案,用小批量数据计算梯度(平衡速度与稳定性)。
五、正规方程(解析解)
对于多变量线性回归,参数的最优解可通过矩阵运算直接求解:\(\theta = (X^T X)^{-1} X^T y\) 其中 X 是 \(m \times (n+1)\) 的设计矩阵(每行是样本特征,第一列为 1),y 是 \(m \times 1\) 的真实值向量。
优点:无需迭代,直接得到最优解。 缺点:当 \(X^T X\) 不可逆(如特征共线性、样本数小于特征数)时失效,且计算复杂度为 \(O(n^3)\)(n 是特征数,不适用于大规模数据)。
六、模型评估指标
1. 均方误差(MSE)
\(\text{MSE} = \frac{1}{m} \sum_{i=1}^{m} (\hat{y}^{(i)} - y^{(i)})^2\) 衡量预测值与真实值的平均平方误差。
2. 均方根误差(RMSE)
\(\text{RMSE} = \sqrt{\text{MSE}}\) 与目标变量同量纲,更直观反映误差大小。
3. 平均绝对误差(MAE)
\(\text{MAE} = \frac{1}{m} \sum_{i=1}^{m} |\hat{y}^{(i)} - y^{(i)}|\) 对异常值更鲁棒(无平方放大误差)。
4. 决定系数(\(R^2\))
\(R^2 = 1 - \frac{\sum_{i=1}^{m} (\hat{y}^{(i)} - y^{(i)})^2}{\sum_{i=1}^{m} (\bar{y} - y^{(i)})^2}\) 表示模型解释的方差比例,\(R^2 \in [0, 1]\),越接近 1 越好。
七、Python 实战:线性回归实现
1. 数据准备(以波士顿房价数据集为例)
python
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score# 加载数据
boston = load_boston()
X = boston.data # 特征
y = boston.target # 目标# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
2. 模型训练与预测
python
# 初始化线性回归模型
model = LinearRegression()# 训练模型
model.fit(X_train, y_train)# 预测
y_pred = model.predict(X_test)# 评估
mse = mean_squared_error(y_test, y_pred)
rmse = mse ** 0.5
r2 = r2_score(y_test, y_pred)print(f"RMSE: {rmse:.2f}, R²: {r2:.2f}")
3. 手动实现梯度下降(单变量示例)
python
import numpy as np# 单变量数据
x = np.array([1, 2, 3, 4, 5])
y = np.array([2, 4, 6, 8, 10]) # 真实关系:y=2x# 初始化参数
theta0, theta1 = 0, 0
alpha = 0.01 # 学习率
m = len(x)# 梯度下降迭代
for epoch in range(1000):y_pred = theta0 + theta1 * xd_theta0 = (1/m) * np.sum(y_pred - y)d_theta1 = (1/m) * np.sum((y_pred - y) * x)theta0 -= alpha * d_theta0theta1 -= alpha * d_theta1print(f"theta0: {theta0:.2f}, theta1: {theta1:.2f}") # 接近0和2
八、优缺点与应用场景
优点
- 简单易解释:模型参数直接反映特征对目标的影响(如 \(\theta_1\) 表示特征 \(x_1\) 每增加 1 单位,y 的变化量)。
- 计算高效:梯度下降和正规方程均可快速求解,适用于中小规模数据。
- 可扩展性:通过特征工程(如多项式回归、交互项)处理非线性关系(本质仍为线性模型,对参数线性)。
缺点
- 对异常值敏感:MSE 损失函数会放大异常值的影响(可改用 MAE 损失缓解)。
- 假设线性关系:若数据非线性,需先进行特征变换(如多项式拟合)。
- 特征共线性:多变量时,共线性会导致参数估计不稳定(可通过正则化或降维处理)。
应用场景
- 预测分析:如销售额预测、股价预测、能源消耗预测。
- 因果分析:量化特征对目标的影响(如广告投入对销量的边际效应)。
- 基线模型:作为复杂模型(如决策树、神经网络)的对比基准,验证模型改进效果。
九、总结
线性回归是机器学习的基石,其核心思想是通过最小化误差平方和来拟合数据。无论是理论推导(损失函数、梯度下降)还是实际应用(代码实现、模型评估),都体现了简洁与高效的特点。掌握线性回归不仅能解决实际问题,还能为理解更复杂的模型(如逻辑回归、岭回归、Lasso 回归)奠定基础。在实践中,需结合数据特点选择优化算法(梯度下降 vs 正规方程),并通过特征工程和正则化提升模型性能,应对非线性和共线性等挑战。
通过本文的解析与实战,相信你已对线性回归有了全面的理解。接下来,不妨尝试用真实数据集(如 Kaggle 上的房价预测数据)进行实践,进一步巩固所学知识!
扩展阅读:
- 统计学中的线性回归与机器学习的异同(强调优化目标与应用场景)。
- 正则化线性回归(岭回归、Lasso):处理过拟合与共线性的方法。
- 多项式回归:通过特征变换实现非线性拟合(本质仍为线性模型,对参数线性)。
希望这篇博客能帮助你深入理解线性回归,开启机器学习的学习之旅!
编辑
分享
线性回归的基本假设和注意事项
写一篇介绍线性回归和逻辑回归的对比博客
提供一些实际的案例,展示线性回归在不同领域的应用
相关文章:

机器学习中的线性回归:从理论到实践的深度解析
一、引言 线性回归(Linear Regression)是机器学习和统计学中最基础且应用广泛的模型之一,用于预测连续型目标变量。它通过建立输入特征与输出变量之间的线性关系,实现对未知数据的预测。无论是预测房价、股票走势,还是…...

【通关文件操作(下)】--文件的顺序读写(续),sprintf和sscanf函数,文件的随机读写,文件缓冲区,更新文件
目录 四.文件的顺序读写(续) 4.8--fwrite函数 4.9--fread函数 五.sprintf函数和sscanf函数 5.1--函数对比 5.2--sprintf函数 5.3--sscanf函数 六.文件的随机读写 6.1--fseek函数 6.2--ftell函数 6.3--rewind函数 七.文件缓冲区 7.1--fflush函数 八.更新文件 &…...

mysql的Memory引擎的深入了解
目录 1、Memory引擎介绍 2、Memory内存结构 3、内存表的锁 4、持久化 5、优缺点 6、应用 前言 Memory 存储引擎 是 MySQL 中一种高性能但非持久化的存储方案,适合临时数据存储和缓存场景。其核心优势在于极快的读写速度,需注意数据丢失风险和内存占…...

尚硅谷-尚庭公寓部署文档
文章目录 整合版部署文档部署架构图1. 项目目录结构增加注释的 Dockerfile 配置(1) 后端服务1 Dockerfile (backend/service1/Dockerfile)(2) 后端服务2 Dockerfile (backend/service2/Dockerfile) Dockerfile 配置说明重要注意事项3. Nginx 配置(1) 主配置文件 (nginx/nginx.c…...

使用函数证明给定的三个数是否能构成三角形
问题描述 给定三条边,请你判断一下能不能组成一个三角形。 输入数据第一行包含一个数M,接下有M行,每行一个实例,包含三个正数A,B,C。其中A,B,C <1000; 对于每个测试实例,如果三条边长A,B,C能组成三角形的话&#x…...

【数据结构】——二叉树堆(下)
一、堆中两个重要的算法 我们前面学习了树的概念和结构,还要树的一种特殊树--二叉树,然后我们学习了堆,知道了堆分为大堆和小堆,接下来我们就使用堆来进行一个排序。 在学习我们的堆排序前,我们先详细学习一下我们堆…...

t009-线上代驾管理系统
项目演示地址 摘 要 使用旧方法对线上代驾管理系统的信息进行系统化管理已经不再让人们信赖了,把现在的网络信息技术运用在线上代驾管理系统的管理上面可以解决许多信息管理上面的难题,比如处理数据时间很长,数据存在错误不能及时纠正等问题…...
目标检测预测框置信度(Confidence Score)计算方式
预测框的置信度(Confidence Score)是目标检测模型输出的一个关键部分,它衡量了模型对一个预测框中包含特定类别对象的确定程度。 不同的目标检测模型(如Faster R-CNN、SSD、YOLO、DETR等)在计算置信度时有其特有的机制…...

【题解-洛谷】B4295 [蓝桥杯青少年组国赛 2022] 报数游戏
题目:B4295 [蓝桥杯青少年组国赛 2022] 报数游戏 题目描述 某班级男生人数为 X X X 人,女生人数为 Y Y Y 人,现全班同学围成一个圆圈,并按照顺时针方向为每名同学编号(从 1 1 1 到 X Y XY XY)。现给…...

Bootstrap项目 - 个人作品与成就展示网站
文章目录 前言一、项目整体概述1. 项目功能介绍1.1 导航栏1.2 首页模块1.3 关于我模块1.4 技能模块1.5 作品模块1.6 成就模块1.7 博客模块1.8 联系我模块 2. 技术选型说明 二、项目成果展示1. PC端展示1.1 首页1.2 关于我1.3 技能1.4 作品1.5 成就1.6 博客1.7 联系我 2. 移动端…...

新能源汽车霍尔线束介绍
新能源汽车作为传统燃油车的重要替代方案,其核心驱动系统依赖于高效、精准的电子控制技术。在这一体系中,霍尔线束作为关键传感器组件,承担着电机转速、位置信号的实时采集与传输任务,其性能直接影响整车动力输出的稳定性和能量利…...

2023网络应用专业-Python程序设计复习题目
2023技校网络应用专业-Python程序设计复习题目 须知: 个人信息要填写正确,在线答题时间不限,可以反复作答,次数不限,最后取最高分。 第一部分:单选题 1. 在Python交互模式下,输入下面代码: >>> “{0:.2f}”.format(12345.6789) 回车后显示的结果为: [单选…...

Termux可用中间人网络测试工具Xerosploit
Termux可用中间人网络测试工具Xerosploit。 Xerosploit 是一款基于 MITM 的本地网络渗透测试工具包。 食用方法: git clone https://github.com/LionSec/xerosploit cd xerosploit sudo python3 install.py 运行: sudo xerosploit 使用备注࿱…...

气镇阀是什么?
01、阀门介绍: 油封机械真空泵的压缩室上开一小孔,并装上调节阀,当打开阀并调节入气量,转子转到某一位置,空气就通过此孔掺入压缩室以降低压缩比,从而使大部分蒸汽不致凝结而和掺入的气体一起被排除泵外起此…...

SmolVLM2: The Smollest Video Model Ever(七)
编写测试代码与评价指标 现在的数据集里面只涉及tool的分类和手术phase的分类,所以编写的评价指标还是那些通用的,但是: predicted_labels:[The current surgical phase is CalotTriangleDissection, Grasper, Hook tool exists., The curre…...

RFID综合项目实训 | 基于C#的一卡通管理系统
目录 基于C#的一卡通管理系统 【实验目的】 【实验设备】 【实验内容】 【实验步骤】 实验准备 第一部分 界面布局设计 第二部分 添加串口通讯函数及高频标签操作功能函数(部分代码) 第五部分 实验运行效果 基于C#的一卡通管理系统 【实验目的】 熟悉 …...
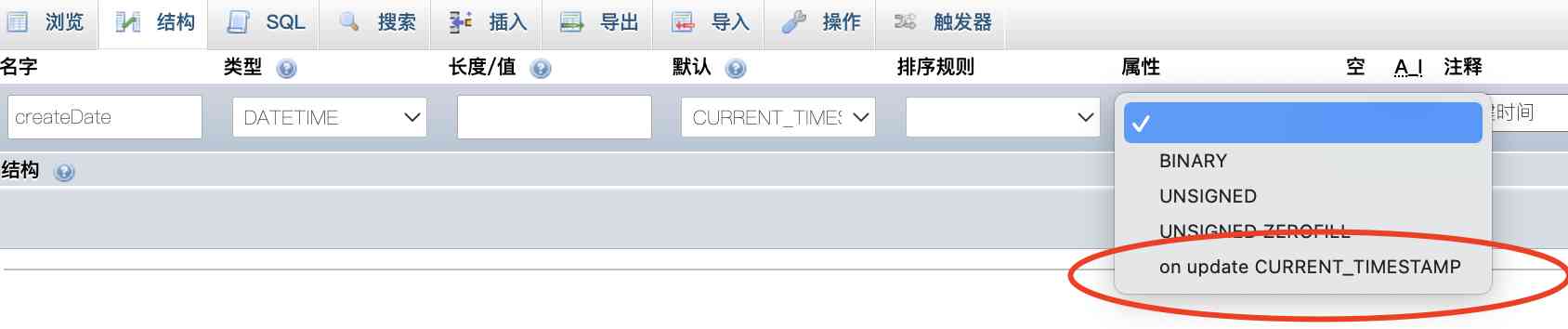
mysql如何设置update时间字段自动更新?
之前在给网站做表设计的时候时间字段都是用的datetime类型,初始值都是设置的CURRENT_TIMESTAMP。 由于给文章表设计的有创建时间和更新时间两个字段,但是更新时间字段需要在更新文章后再次更新,当时由于不了解mysql还可以设置自动更新时间戳…...

数据库备份与恢复专业指南
数据库备份与恢复专业指南 一、备份与恢复核心概念 关键结论:数据库备份是数据安全的最后防线,恢复能力才是真正的备份有效性检验标准。 AI大模型专栏:https://duoke360.com/tutorial/path/ai-lm 1.1 备份类型 物理备份:直接复制数据库文件(如MySQL的.ibd文件、Oracle的.d…...

【第4章 图像与视频】4.5 操作图像的像素
文章目录 前言示例-获取和修改图像数据图像数据的遍历方式图像滤镜负片滤镜黑白滤镜浮雕滤镜filter滤镜属性 前言 getImageData() 与 putImageData() 这两个方法分别用来获取图像的像素信息,以及向图像中插入像素。与此同时,如果有需要,也可…...

Science Advances 上海理工大学与美国杜克大学(Duke University)共同开发了一种仿生复眼相机
编辑丨%科学家开发了一种 AI 辅助的仿生复眼相机。炎炎夏日,相信各位读者都有被蚊子骚扰过的恼火记忆。但往往想要清剿蚊子的时候,却被它灵巧地躲开,再难找到。诸如蚊子这种节肢动物的视觉系统已经进化了 5 亿多年,从寒武纪一直到…...

正点原子Z20 ZYNQ 开发板发布!板载FMC LPC、LVDS LCD和WIFI蓝牙等接口,资料丰富!
正点原子Z20 ZYNQ 开发板发布!板载FMC LPC、LVDS LCD和WIFI&蓝牙等接口,资料丰富! 正点原子新品Z20 ZYNQ开发板来啦!核心板全工业级设计,主控芯片型号是XC7Z020CLG484-2I。开发板由核心板底板组成&…...

软件测评中心如何确保软件品质?需求分析与测试计划很关键
软件测评中心承担着对软件进行评估、测试和审查的任务,它有一套规范的流程来确保软件的品质,并且能够向客户和开发者提供详实的软件状况分析报告。 需求分析环节 这一环节至关重要,必须与客户和开发团队保持密切交流。我们需要从他们那里精…...
)
004 flutter基础 初始文件讲解(3)
之前,我们正向的学习了一些flutter的基础,如MaterialApp,Scaffold之类的东西,那么接下来,我们将正式接触原代码: import package:flutter/material.dart;void main() {runApp(const MyApp()); }class MyAp…...

2025LitCTF 复现
easy_file 登录界面 尝试admin 和密码1 没成功 结果尝试了弱口令 admin 用户和 password 密码就登录成功了 文件上传 新建一个空的 新建木马.txt 文件发现上传成功 然后写入一句话木马 <?php eval($_POST[a]); ?> 上传失败 说明可能是有字符被过滤了,猜…...

英语中最难学的部分是时态
英语中最难学的部分是时态。英语的时态体系包含16种时态,每种时态都有其独特的用法和规则,这使得时态成为英语学习中的一个难点 。 时态的定义和分类 时态可以分为时间和体态两个维度: 时间:现在时、过去时、将来时、过…...

Python 如何让自动驾驶的“眼睛”和“大脑”真正融合?——传感器数据融合的关键技术解析
Python 如何让自动驾驶的“眼睛”和“大脑”真正融合?——传感器数据融合的关键技术解析 自动驾驶技术从来都不是“单兵作战”。如果你细看一辆自动驾驶汽车,它其实是一个传感器的集合体:摄像头、激光雷达(LiDAR)、毫米波雷达、超声波传感器、GPS……这些传感器各自发挥作…...

使用C# 快速删除Excel表格中的重复行数据-详解
目录 简介 使用工具 C# 删除Excel工作表中的重复行 C# 删除指定Excel单元格区域中的重复行 C# 基于特定列删除重复行 RemoveDuplicates 方法快速比较 简介 重复行是指在Excel表格中完全相同的多行数据。这些冗余行的存在可能源于多种原因,例如: …...

WPF-Prism学习笔记之 “导航功能和依赖注入“
新建空白模板(Prism) 新建好后会有自动创建ViewModels和Views 在"MainWindow.xaml"文件里面标题去绑定了一个属性"Title",而"MainWindowViewModel.cs"里面继承一个非常重要的"BindbleBase"(prism框架里面非常重要的)。所以…...

中国城市间地理距离矩阵(2024)
1825 中国城市间地理距离矩阵(2024) 数据简介 中国城市间地理距离矩阵数据集,通过审图号GS(2024)0650的中国城市地图在Albers投影坐标系中进行计算得出矩阵表格,单位为KM,方便大家研究使用。 中国城市地理距离矩阵数据通过计算城市中心距离…...

【孙悟空喝水】2022-2-7
缘由C编程问题求解:9634: 孙悟空喝水-编程语言-CSDN问答 void 孙悟空喝水() {//缘由https://ask.csdn.net/questions/7639865?spm1005.2025.3001.5141int x 2, n 0; double s 0, ss 0;std::cin >> n;while ((int)s < n)s 1.0 / x, ss (x - 1.0) / …...
