力扣每日一题——找到离给定两个节点最近的节点

目录
题目链接:2359. 找到离给定两个节点最近的节点 - 力扣(LeetCode)
题目描述
解法一:双指针路径交汇法
基本思路
关键步骤
为什么这样可行呢我请问了?
举个例子
特殊情况
Java写法:
C++写法:
运行时间
时间复杂度和空间复杂度
总结
题目链接:2359. 找到离给定两个节点最近的节点 - 力扣(LeetCode)
注:下述题目描述和示例均来自力扣
题目描述
给你一个 n 个节点的 有向图 ,节点编号为 0 到 n - 1 ,每个节点 至多 有一条出边。
有向图用大小为 n 下标从 0 开始的数组 edges 表示,表示节点 i 有一条有向边指向 edges[i] 。如果节点 i 没有出边,那么 edges[i] == -1 。
同时给你两个节点 node1 和 node2 。
请你返回一个从 node1 和 node2 都能到达节点的编号,使节点 node1 和节点 node2 到这个节点的距离 较大值最小化。如果有多个答案,请返回 最小 的节点编号。如果答案不存在,返回 -1 。
注意 edges 可能包含环。
示例 1:

输入:edges = [2,2,3,-1], node1 = 0, node2 = 1 输出:2 解释:从节点 0 到节点 2 的距离为 1 ,从节点 1 到节点 2 的距离为 1 。 两个距离的较大值为 1 。我们无法得到一个比 1 更小的较大值,所以我们返回节点 2 。
示例 2:

输入:edges = [1,2,-1], node1 = 0, node2 = 2 输出:2 解释:节点 0 到节点 2 的距离为 2 ,节点 2 到它自己的距离为 0 。 两个距离的较大值为 2 。我们无法得到一个比 2 更小的较大值,所以我们返回节点 2 。
提示:
n == edges.length2 <= n <= 105-1 <= edges[i] < nedges[i] != i0 <= node1, node2 < n
解法一:双指针路径交汇法
这道题目的核心是在一个有向图中,每个节点最多只有一条出边,可能存在环。给定两个起点 node1 和 node2,要找一个节点 x,使得两个起点都能到达 x,并且两个起点到 x 的距离中较大的那个值尽可能小。如果多个节点满足条件,选编号最小的;如果不存在,返回 -1。
基本思路
因为每个节点最多只有一条出边,整个图的结构其实很简单:从任意节点出发,沿着出边走,要么走到尽头(遇到 -1),要么进入一个环然后开始循环。这种结构决定了从 node1 或 node2 出发的路径是唯一的,不会分叉,只是可能绕圈。
关键步骤
-
分别计算两个起点能到达哪些节点
用两个数组(比如dist1和dist2)记录 node1 和 node2 到每个节点的距离。初始化时都设为 -1,表示不可达。然后从 node1 出发,沿着出边走,每走一步记录当前步数(距离),直到走到尽头或遇到已经访问过的节点(说明进入环了,再走会重复,此时停掉)。对 node2 同样操作一遍。 -
处理环的干扰
如果路径进入环,比如从 node1 走到节点 A 后开始绕圈,那么第一次走到 A 时的距离就是最短距离。之后再绕圈只会让距离变大,所以遇到访问过的节点直接停掉,避免死循环。 -
找最优节点
遍历所有节点,如果一个节点在dist1和dist2中都有记录(说明两个起点都能到达它),就计算max(dist1[i], dist2[i])(即两个距离的较大值)。我们需要的正是这个较大值最小的节点。如果有多个节点值相同,选编号最小的那个。
为什么这样可行呢我请问了?
- 路径唯一性:因为每个节点最多一条出边,从起点出发的路径是唯一的,不会分叉,所以记录的距离就是最短距离。
- 环的处理:遇到环就停,保证了第一次到达节点的距离是最小的,后续绕圈只会增加距离,不用考虑。
- 最优解筛选:直接比较所有公共节点的距离较大值,取最小值,符合题目要求。
举个例子
假设图是 edges = [2, 2, 3, -1],node1=0,node2=1:
- node1(0)的路径:0 → 2 → 3,距离
dist1[2]=1,dist1[3]=2。 - node2(1)的路径:1 → 2 → 3,距离
dist2[2]=1,dist2[3]=2。
公共节点是 2 和 3。节点 2 的较大值是max(1,1)=1,节点 3 是max(2,2)=2,所以选节点 2。
特殊情况
如果两个起点没有公共可达节点(比如一个走到尽头,另一个进环但路径不重合),直接返回 -1。
Java写法:
class Solution {public int closestMeetingNode(int[] edges, int node1, int node2) {int n = edges.length;int[] dist1 = new int[n];int[] dist2 = new int[n];Arrays.fill(dist1, -1);Arrays.fill(dist2, -1);// 计算 node1 到各节点的距离int cur = node1, steps = 0;while (cur != -1 && dist1[cur] == -1) {dist1[cur] = steps++;cur = edges[cur];}// 计算 node2 到各节点的距离cur = node2;steps = 0;while (cur != -1 && dist2[cur] == -1) {dist2[cur] = steps++;cur = edges[cur];}// 寻找最优节点int minMaxDist = Integer.MAX_VALUE;int ans = -1;for (int i = 0; i < n; i++) {if (dist1[i] != -1 && dist2[i] != -1) {int maxDist = Math.max(dist1[i], dist2[i]);if (maxDist < minMaxDist || (maxDist == minMaxDist && i < ans)) {minMaxDist = maxDist;ans = i;}}}return ans;}
}C++写法:
#include <vector>
#include <climits>
#include <algorithm>
using namespace std;class Solution {
public:int closestMeetingNode(vector<int>& edges, int node1, int node2) {int n = edges.size();vector<int> dist1(n, -1);vector<int> dist2(n, -1);// 计算 node1 到各节点的距离int cur = node1, steps = 0;while (cur != -1 && dist1[cur] == -1) {dist1[cur] = steps++;cur = edges[cur];}// 计算 node2 到各节点的距离cur = node2;steps = 0;while (cur != -1 && dist2[cur] == -1) {dist2[cur] = steps++;cur = edges[cur];}// 寻找最优节点int minMaxDist = INT_MAX;int ans = -1;for (int i = 0; i < n; i++) {if (dist1[i] != -1 && dist2[i] != -1) {int maxDist = max(dist1[i], dist2[i]);if (maxDist < minMaxDist || (maxDist == minMaxDist && i < ans)) {minMaxDist = maxDist;ans = i;}}}return ans;}
};运行时间

时间复杂度和空间复杂度
时间复杂度:O(n)
空间复杂度:O(n)
总结
问题核心:给定一个有向图(节点最多一条出边,可能存在环),需找到节点 node1 和 node2 均可达的节点,使两者到该节点距离的较大值最小化。若有多个解,返回最小节点编号;无解则返回 -1。
解法精髓:采用 双指针路径交汇法(Dual-Pointer Path Convergence)
相关文章:

力扣每日一题——找到离给定两个节点最近的节点
目录 题目链接:2359. 找到离给定两个节点最近的节点 - 力扣(LeetCode) 题目描述 解法一:双指针路径交汇法 基本思路 关键步骤 为什么这样可行呢我请问了? 举个例子 特殊情况 Java写法: C写法&a…...

机器学习与深度学习03-逻辑回归01
目录 上集回顾1. 逻辑回归与线性回归的区别2.逻辑回归的常见目标函数3.逻辑回归如何分类4.Sigmoid函数详解5.逻辑回归模型的参数 上集回顾 上一节文章地址:链接 1. 逻辑回归与线性回归的区别 应用领域 线性回归通常⽤于解决回归问题,其中⽬标是预测⼀…...

卷积神经网络(CNN)入门学习笔记
什么是 CNN? CNN,全称 卷积神经网络(Convolutional Neural Network),是一种专门用来处理图片、语音、文本等结构化数据的神经网络。 它模仿人眼识别图像的方式: 从局部到整体,一步步提取特征&a…...

【优笔】基于STM32的多模态智能门禁系统
代码功能详细描述 该代码实现了一个基于STM32的多模态智能门禁系统,整合密码、指纹、人脸识别(预留)三种验证方式,并提供完善的管理功能。系统架构如下图所示: #mermaid-svg-Uufpcoeo5Lega096 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size…...
丨小白WEB安全入门笔记)
Metasploit工具使用详解(上)丨小白WEB安全入门笔记
Metasploit工具使用详解(上)丨小白WEB安全入门笔记 一、课程定位与工具概述 课程性质: 小白WEB安全入门课程聚焦基础操作,非深度专题(Metasploit专题可讲数十节课)目标:掌握基本概念和简单漏洞利用 Metasploit核心定…...

Femap许可证与网络安全策略
随着科技的快速发展,网络安全问题已成为各行各业关注的焦点。在电磁仿真领域,Femap作为一款领先的软件,其许可证的安全性和网络策略的重要性不言而喻。本文将探讨Femap许可证与网络安全策略的关系,确保您的电磁仿真工作能够在一个…...
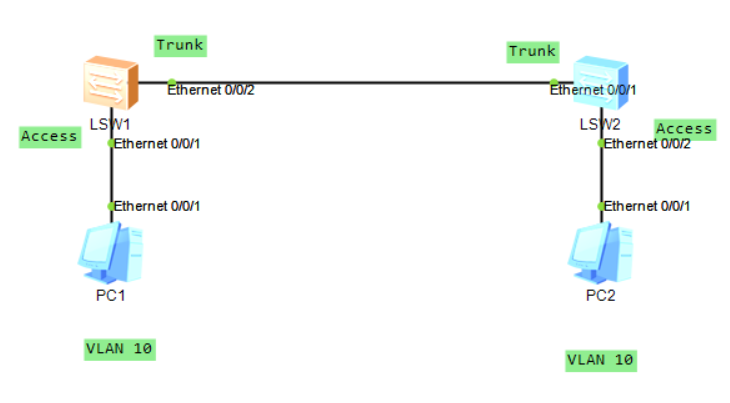
VLAN的作用和原理
1. 为什么要有vlan? 分割广播域,避免广播风暴,造成网络资源的浪费 可以灵活的组网,便于管理,同时还有安全加固的功能 2. vlan是怎么实现的?端口的原理? 设置VLAN后,流量之间的转…...

深入探讨集合与数组转换方法
目录 1、Arrays.asList() 1.1、方法作用 1.2、内部实现 1.3、修改元素的影响 1.4、注意事项 2、list.toArray() 2.1、方法作用 2.2、内部实现 2.3、修改元素的影响 2.4、特殊情况 1、对象引用 2、数组copy 3、对比总结 4、常见误区与解决方案 5、实际应用建议…...

让大模型看得见自己的推理 — KnowTrace结构化知识追踪
让大模型“看得见”自己的推理 —— KnowTrace 结构化知识追踪式 RAG 全解析 一句话概括:把检索-推理“改造”成 动态知识图构建任务,再让 LLM 只关注这张不断精炼的小图 —— 这就是显式知识追踪的核心价值。 1. 背景:为什么 RAG 仍难以搞定多跳推理? 长上下文负担 传统 I…...

【HarmonyOS 5应用架构详解】深入理解应用程序包与多Module设计机制
⭐本期内容:【HarmonyOS 5应用架构详解】深入理解应用程序包与多Module设计机制 🏆系列专栏:鸿蒙HarmonyOS:探索未来智能生态新纪元 文章目录 前言应用与应用程序包应用程序的基本概念应用程序包的类型标识机制应用安装流程 应用的…...

【Oracle】DCL语言
个人主页:Guiat 归属专栏:Oracle 文章目录 1. DCL概述1.1 什么是DCL?1.2 DCL的核心功能 2. 用户管理2.1 创建用户2.2 修改用户2.3 删除用户2.4 用户信息查询 3. 权限管理3.1 系统权限3.1.1 授予系统权限3.1.2 撤销系统权限 3.2 对象权限3.2.1…...

MySQL强化关键_017_索引
目 录 一、概述 二、索引 1.主键索引 2.唯一索引 3.查看索引 4.添加索引 (1)建表时添加 (2)建表后添加 5.删除索引 三、树 1.二叉树 2.红黑树 3.B树 4.B树 (1)为什么 MySQL 选择B树作为索引…...

stm32——SPI协议
stm32——SPI协议 STM32的SPI(Serial Peripheral Interface,串行外设接口)协议是一种高速、全双工、同步的串行通信协议,广泛评估微控制器与各种外设(如传感器、器件、显示器、模块等)之间的数据传输。STM3…...

Linux 下如何查看进程的资源限制信息?
简介 Linux 上的 cat /proc/$pid/limits 命令提供有关特定进程的资源限制的信息,其中 $pid 是相关进程的进程 ID (pid)。该文件是 /proc 文件系统的一部分,该文件系统是一个虚拟文件系统,提供有关进程和系统资源的信息…...

【备忘】php命令行异步执行超长时间任务
环境说明: 操作系统:windows10 IDE:phpstorm 开发语言:php7.4 框架:thinkphp5.1 测试环境:linuxwindows均测试通过。 初级方法: function longRunningTask() {$root_path Tools::get_ro…...

对于ARM开发各种手册的分类
手册名称全称主要内容适用范围是不是讲SysTick?Cortex-M3 Technical Reference Manual (TRM)Cortex-M3 Technical Reference Manual描述 Cortex-M3内核架构,如寄存器模型、总线接口、指令集、异常模型只适合 Cortex-M3 内核,不含外设❌ 没有C…...

java开发中#和$的区别
在Spring框架中,$ 和 # 是两种不同的表达式前缀,用于从不同的来源获取值或执行计算。下面详细解释它们的区别和用法: 一、$ 占位符(Property Placeholder) 1. 作用 从配置文件(如 application.propertie…...

在 RK3588 上通过 VSCode 远程开发配置指南
在 RK3588 上通过 VSCode 远程开发配置指南 RK3588 设备本身不具备可视化编程环境,但可以通过 VSCode 的 Remote - SSH 插件 实现远程代码编写与调试。以下是完整的配置流程。 一、连接 RK3588 1. 安装 Debian 系统 先在 RK3588 上安装 Debian 操作系统。 2. 安…...

OpenHarmony标准系统-HDF框架之音频驱动开发
文章目录 引言OpenHarmony音频概述OpenHarmony音频框图HDF音频驱动框架概述HDF音频驱动框图HDF音频驱动框架分析之音频设备驱动HDF音频驱动框架分析之supportlibs实现HDF音频驱动框架分析之hdi-passthrough实现HDF音频驱动框架分析之hdi-bindev实现HDF音频驱动加载过程HDF音频驱…...

HTML Day03
Day03 0. 引言1. CSS1.1 CSS的3种使用方法1.2 内联样式1.3 内部样式表1.4 外部CSS文件 2. 图像3. 表格3.1单元格间距和单元格边框 4. 列表4.1 有序表格的不同类型4.2 不同类型的无序表格4.3 嵌套列表 5. 区块6. 布局6.1 div布局6.2 表格布局 0. 引言 HELLO ^ _ ^大家好…...

篇章六 数据结构——链表(二)
目录 1. LinkedList的模拟实现 1.1 双向链表结构图编辑 1.2 三个简单方法的实现 1.3 头插法 1.4 尾插法 1.5 中间插入 1.6 删除 key 1.7 删除所有key 1.8 clear 2.LinkedList的使用 2.1 什么是LinkedList 5.2 LinkedList的使用 1.LinkedList的构造 2. LinkedList的…...

Python60日基础学习打卡Day39
昨天我们介绍了图像数据的格式以及模型定义的过程,发现和之前结构化数据的略有不同,主要差异体现在2处 模型定义的时候需要展平图像由于数据过大,需要将数据集进行分批次处理,这往往涉及到了dataset和dataloader来规范代码的组织…...

吴恩达MCP课程(3):mcp_chatbot
原课程代码是用Anthropic写的,下面代码是用OpenAI改写的,模型则用阿里巴巴的模型做测试 .env 文件为: OPENAI_API_KEYsk-xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx OPENAI_API_BASEhttps://dashscope.aliyuncs.com/compatible-mode…...

MySQL访问控制与账号管理:原理、技术与最佳实践
MySQL的安全体系建立在精细的访问控制和账号管理机制上。本文基于MySQL 9.3官方文档,深入解析其核心原理、关键技术、实用技巧和行业最佳实践。 一、访问控制核心原理:双重验证机制 连接验证 (Connection Verification) 客户端发起连接时,MyS…...

AWS 创建VPC 并且添加权限控制
AWS 创建VPC 并且添加权限控制 以下是完整的从0到1在AWS中创建VPC并配置权限的步骤(包含网络配置、安全组权限和实例访问): 1. 创建VPC 步骤: 登录AWS控制台 访问 AWS VPC控制台,点击 创建VPC。 配置基础信息 名称…...

langchain学习 01
dotenv库:可以从.env文件中加载配置信息。 from dotenv import load_dotenv # 加载函数,之后调用这个函数,即可获取配置环境.env里面的内容: deep_seek_api_key<api_key>getpass库:从终端输入password性质的内…...
【清晰教程】查看和修改Git配置情况
目录 查看安装版本 查看特定配置 查看全局配置 查看本地仓库配置 设置或修改配置 查看安装版本 打开命令行工具,通过version命令检查Git版本号。 git --version 如果显示出 Git 的版本号,说明 Git 已经成功安装。 查看特定配置 如果想要查看特定…...

JAVA 常用 API 正则表达式
1 正则表达式作用 作用一:校验字符串是否满足规则作用二:在一段文本中查找满足要求的内容 2 正则表达式规则 2.1 字符类 package com.bjpowernode.test14;public class RegexDemo1 {public static void main(String[] args) {//public boolean matche…...

光电设计大赛智能车激光对抗方案分享:低成本高效备赛攻略
一、赛题核心难点与备赛痛点解析 全国大学生光电设计竞赛的 “智能车激光对抗” 赛题,要求参赛队伍设计具备激光对抗功能的智能小车,需实现光电避障、目标识别、轨迹规划及激光精准打击等核心功能。从历年参赛情况看,选手普遍面临三大挑战&a…...

Python实现P-PSO优化算法优化BP神经网络回归模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在当今数据驱动的时代,回归分析作为预测和建模的重要工具,在科学研究和工业应用中占据着重要…...
