复数三角不等式简介及 MATLAB 演示
复数三角不等式简介及 MATLAB 演示
1. 复数三角不等式简介
复数三角不等式(Complex Triangle Inequality)是复数的一种重要性质,它类似于普通的三角不等式,但适用于复数空间。具体来说,复数三角不等式可以描述复数之间的几何关系。
对于任意两个复数 z 1 z_1 z1 和 z 2 z_2 z2 ,复数三角不等式的表达式为:
∣ z 1 + z 2 ∣ ≤ ∣ z 1 ∣ + ∣ z 2 ∣ |z_1 + z_2| \leq |z_1| + |z_2| ∣z1+z2∣≤∣z1∣+∣z2∣
这里, ∣ z ∣ |z| ∣z∣ 表示复数 z z z 的模,也即其在复平面上的距离原点的距离。几何意义上,这个不等式表明,两个复数和的模不超过它们各自模的和。
- 等式成立的条件: 当且仅当 z 1 z_1 z1 和 z 2 z_2 z2 在复平面上共线且方向相同时,等式才成立。
2. 复数三角不等式的几何解释
在复平面中,每个复数可以看作是一个点或者向量。复数 z 1 z_1 z1 和 z 2 z_2 z2 可以表示为从原点出发的两个向量,复数 z 1 + z 2 z_1 + z_2 z1+z2 则是这两个向量的和,也就是从原点出发,沿着两个向量的路径得到的新向量。
复数三角不等式的几何含义是:两个向量的和的长度不大于它们各自长度之和。若两个向量在同一方向上,则它们的和的长度等于它们长度之和;如果它们的方向不同,则它们的和的长度小于它们长度之和。
3. 使用 MATLAB 演示复数三角不等式
在 MATLAB 中,我们可以通过画图和计算复数的模来验证复数三角不等式。下面是一个简单的示例,演示了两个复数的和以及三角不等式的验证。
% 定义复数 z1 和 z2
z1 = 4 + i; % 复数 z1 = 3 + 4i
z2 = 1 + 2i; % 复数 z2 = 1 + 2i% 计算复数的模
mod_z1 = abs(z1);
mod_z2 = abs(z2);
mod_z1_plus_z2 = abs(z1 + z2);% 显示复数模的结果
disp(['|z1| = ', num2str(mod_z1)]);
disp(['|z2| = ', num2str(mod_z2)]);
disp(['|z1 + z2| = ', num2str(mod_z1_plus_z2)]);
disp(['|z1 + z2| <= |z1| + |z2|: ', num2str(mod_z1_plus_z2 <= (mod_z1 + mod_z2))]);% 绘制复数 z1 和 z2 的向量图形
figure;
hold on;
quiver(0, 0, real(z1), imag(z1), 0, ...'r', 'LineWidth', 2); % 绘制 z1 的向量
quiver(0, 0, real(z2), imag(z2), 0, ...'b', 'LineWidth', 2,'MaxHeadSize',0.5); % 绘制 z2 的向量
quiver(0, 0, real(z1 + z2), imag(z1 + z2), 0,...'g', 'LineWidth', 2); % 绘制 z1 + z2 的向量
quiver(4, 1, real(z2), imag(z2), 0, ...'-.b', 'LineWidth', 2,'MaxHeadSize',0.5); % 绘制 z3 的向量,z2向量平移到在末端% 设置图形属性
axis equal;
xlim([0 6]);
ylim([0 6]);
grid on;
title('复数向量示意图');
legend('z1', 'z2', 'z1 + z2');
hold off;输出结果:最后输出的1,代表等式成立

4. 代码解释
- 复数定义:我们定义了两个复数 z 1 = 4 + i z_1 = 4+ i z1=4+i 和 z 2 = 1 + 2 i z_2 = 1 + 2i z2=1+2i 。
- 模计算:使用 MATLAB 的
abs()函数计算复数的模。我们计算了单个复数 z 1 z_1 z1 和 z 2 z_2 z2 的模,及其和 z 1 + z 2 z_1 + z_2 z1+z2 的模。 - 三角不等式验证:通过输出验证复数三角不等式是否成立,即是否满足 ∣ z 1 + z 2 ∣ ≤ ∣ z 1 ∣ + ∣ z 2 ∣ |z_1 + z_2| \leq |z_1| + |z_2| ∣z1+z2∣≤∣z1∣+∣z2∣。
- 图形绘制:我们使用
quiver()函数绘制了复数 z 1 z_1 z1 、 z 2 z_2 z2 和它们的和 z 1 + z 2 z_1 + z_2 z1+z2 的向量图。不同颜色的箭头表示不同的向量,绿色的箭头表示 z 1 + z 2 z_1 + z_2 z1+z2 的和。
5. 结果分析
通过运行上面的 MATLAB 代码,我们可以观察到,三个向量在复平面中的位置关系以及它们的长度满足复数三角不等式。特别是,当两个复数在同一方向时,和的长度正好等于它们模的和;当它们方向不同,和的长度则小于模的和。

6. 总结
复数三角不等式是复数理论中的一个基本概念,具有重要的几何意义。通过 MATLAB 的可视化,我们不仅可以直观地看到复数和的关系,还能加深对三角不等式几何意义的理解。这个不等式在复分析、信号处理等领域都有着广泛的应用。
相关文章:

复数三角不等式简介及 MATLAB 演示
复数三角不等式简介及 MATLAB 演示 1. 复数三角不等式简介 复数三角不等式(Complex Triangle Inequality)是复数的一种重要性质,它类似于普通的三角不等式,但适用于复数空间。具体来说,复数三角不等式可以描述复数之…...

【Doris基础】Apache Doris 基本架构深度解析:从存储到查询的完整技术演进
目录 1 引言 2 Doris 架构全景图 2 核心组件技术解析 2.1 Frontend 层(FE) 2.2 Backend 层(BE) 3 数据存储与复制机制 3.1 存储架构演进 3.2 副本复制策略 4 查询处理全流程解析 4.1 查询生命周期 5 高可用设计 5.1 F…...
程序人生-hellohelloo
计算机系统 大作业 题 目 程序人生-Hello’s P2P 专 业 计算机与电子通信 学 号 2023111976 班 级 23L0504 学 生 孙恩旗 指 导 教 师 刘宏伟 计算机科…...

ASP.NET Core SignalR的基本使用
文章目录 前言一、SignalR是什么?在 ASP.NET Core 中的关键特性:SignalR 工作原理简图: 二、使用步骤1.创建ASP.NET Core web Api 项目2.添加 SignalR 包3.创建 SignalR Hub4.配置服务与中间件5.创建控制器(模拟服务器向客户端发送消息)6.创建…...
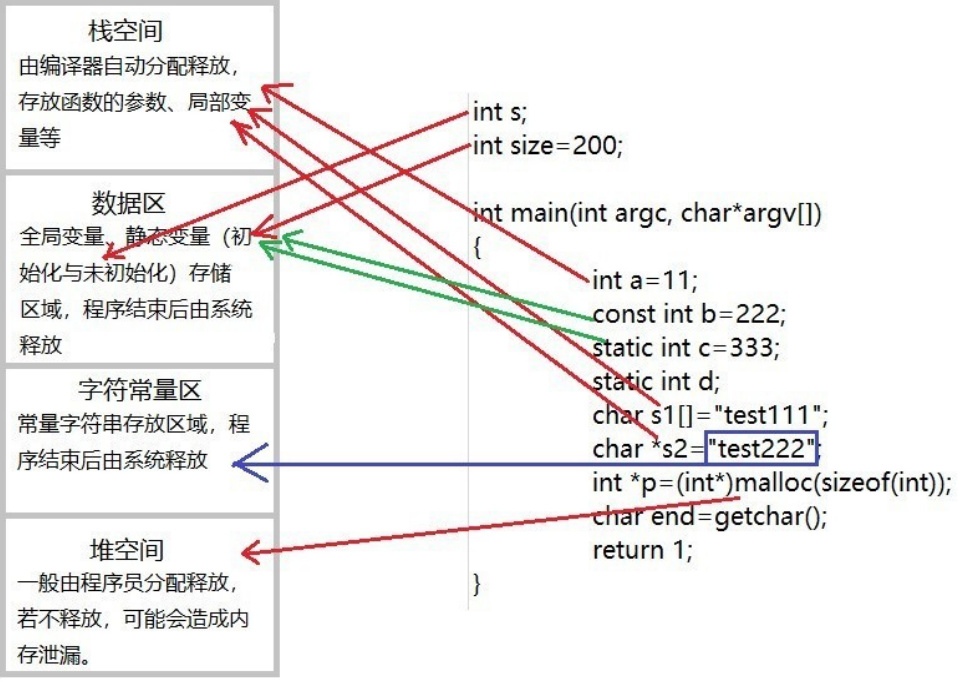
【C语言】讲解 程序分配的区域(新手)
目录 代码区 数据区 堆区 栈区 常量区 重点比较一下堆区与 栈区 总结: 前言: C语言程序的内存分配区域是理解其运行机制的重要部分。根据提供的多条证据,我们可以总结出C语言程序在运行时主要涉及以下五个关键内存区域: 代…...

【脚本 完全参数化的通用 APT 源配置方案-Debian/Ubuntu】
通过脚本在 Debian/Ubuntu 系统上一键切换 APT 源 如Dockerfile中 使用某个源(比如 aliyun) 假设你的目录结构是: . ├── Dockerfile └── switch-apt-source.shFROM ubuntu:22.04# 把脚本拷贝到镜像中 COPY switch-apt-source.sh /us…...

数据集笔记:SeekWorld
提出了一项新任务:地理定位推理(Geolocation Reasoning) 该任务要求模型在感知视觉信息的同时,推理出图像中视觉语义所隐含的高级逻辑关系,从而确定图像的拍摄地点 TheEighthDay/SeekWorld at main 构建了一个基于规则…...

LeetCode 算 法 实 战 - - - 移 除 链 表 元 素、反 转 链 表
LeetCode 算 法 实 战 - - - 移 除 链 表 元 素、反 转 链 表 第 一 题 - - - 移 除 链 表 元 素方 法 一 - - - 原 地 删 除方 法 二 - - - 双 指 针方 法 三 - - - 尾 插 第 二 题 - - - 反 转 链 表方 法 一 - - - 迭 代方 法 二 - - - 采 用 头 插 创 建 新 链 表 总 结 &a…...
:pipeline构建历史展示包名和各阶段间传递参数)
Jenkins实践(10):pipeline构建历史展示包名和各阶段间传递参数
Jenkins实践(10):构建历史展示包名和pipeline各阶段间传递参数 1、构建历史展示包名 参考:https://blog.csdn.net/fen_fen/article/details/148167868 1.1、方法说明 Jenkins版本:Jenkins2.452 通过修改 currentBuild.displayName 和 currentBuild.description 实现: …...
从头认识AI-----循环神经网络(RNN)
前言 前面我们讲了传统的神经网络,如MLP、CNN,这些网络中的输入都被单独处理,没有上下文之间的信息传递机制,这在处理序列数据(如语音、文本、时间序列)时很鸡肋: 如何理解一句话中“前后文”的…...

配置远程无密登陆ubuntu服务器时无法连接问题排查
配置远程无密登陆ubuntu服务器时无法连接问题排查 登陆端排查服务器端登陆排查 登陆端排查 ssh -v 用户名Ubuntu服务器IP可能日志输出 debug1: Authentications that can continue: publickey,password服务器端登陆排查 sudo tail -f /var/log/auth.log可能日志输出 Authen…...

5.31 数学复习笔记 22
前面的笔记,全部写成一段,有点难以阅读。现在改进一下排版。另外,写笔记实际上就是图一个放松呢,关键还是在于练习。 目前的计划是,把讲义上面的高数例题搞清楚之后,大量刷练习册上面的题。感觉不做几本练…...

kafka学习笔记(三、消费者Consumer使用教程——使用实例及及核心流程源码讲解)
1.核心概念与架构 1.1.消费者与消费者组 Kafka消费者是订阅主题(Topic)并拉取消息的客户端实例,其核心逻辑通过KafkaConsumer类实现。消费者组(Consumer Group)是由多个逻辑关联的消费者组成的集合。 核心规则 同一…...

鸿蒙 Form Kit(卡片开发服务)
Form Kit(卡片开发服务) 鸿蒙应用中,Form / Card / Widget 都翻译为“卡片” Form Kit(卡片开发服务)提供一种界面展示形式,可以将应用的重要信息或操作前置到服务卡片,以达到服务直达、减少跳转…...

算力卡上部署OCR文本识别服务与测试
使用modelscope上的图像文本行检测和文本识别模型进行本地部署并转为API服务。 本地部署时把代码中的检测和识别模型路径改为本地模型的路径。 关于模型和代码原理可以参见modelscope上这两个模型相关的页面: iic/cv_resnet18_ocr-detection-db-line-level_damo iic…...

KWIC—Implicit Invocation
KWIC—Implicit Invocation ✏️ KWIC—Implicit Invocation 文章目录 KWIC—Implicit Invocation📝KWIC—Implicit Invocation🧩KWIC🧩核心组件🧩ImplementationScheme⚖️ 隐式调用 vs 显式调用对比 🌟 总结 &#x…...

Visual Studio 2022 发布独立的 exe 文件
我们在用 Visual Studio 2022 写好一个 exe 程序之后,如果想把这个拿到其他地方运行,需要把 exe 所在的文件夹一起拿过去。 编译出来的 exe 文件需要其他几个文件一同放在同一目录才能运行,原因在于默认情况下,Visual Studio 是把…...

11.4java语言执行浅析4
编译成字节码(.class 文件) 使用 javac 命令将源代码编译为 Java 字节码(bytecode) 它不是机器码,而是 JVM 能理解的中间语言(字节码),具有平台无关性。 编译过程简要࿱…...

Excel 操作 转图片,转pdf等
方式一 spire.xls.free(没找设置分辨率的方法) macOs开发Java GUI程序提示缺少字体问题解决 Spire.XLS:一款Excel处理神器_spire.xls免费版和收费版的区别-CSDN博客 官方文档 Spire.XLS for Java 中文教程 <dependency><groupI…...

说说 Kotlin 中的 Any 与 Java 中的 Object 有何异同?
在 Kotlin 中 Any 类型和 Java 中的 Object 类都是所有类型的根类型。 1 基本定义 Kotlin 中的 Any 和 Any?: Any:是所有非空类型的根类型;Any?:是所有可空类型的根类型; Java 中的 Object: 是所有类…...

python分配方案数 2023年信息素养大赛复赛/决赛真题 小学组/初中组 python编程挑战赛 真题详细解析
python分配方案数 2023全国青少年信息素养大赛Python编程挑战赛复赛真题解析 博主推荐 所有考级比赛学习相关资料合集【推荐收藏】1、Python比赛 信息素养大赛Python编程挑战赛 蓝桥杯python选拔赛真题详解...

《信号与系统》第 5 章 离散时间傅里叶变换
5.0 引言 这一章将介绍并研究离散时间傅里叶变换,这样就完整地建立了傅里叶分析方法。 5.1 非周期信号的表示:离散时间傅里叶变换 5.1.1 离散时间傅里叶变换的导出 在第4章看到:一个连续时间周期方波的傅里叶级数可以看成一个包络函数的采…...

动态IP与区块链:重构网络信任的底层革命
在数字经济蓬勃发展的今天,网络安全与数据隐私正面临前所未有的挑战。动态IP技术与区块链的深度融合,正在构建一个去中心化、高可信的网络基础设施,为Web3.0时代的到来奠定基础。 一、技术碰撞:动态IP与区块链的天然契合 动态I…...

目前主流图像分类模型的详细对比分析
以下是目前主流图像分类模型的详细对比分析,结合性能、架构特点及应用场景进行整理: 一、主流模型架构分类与定量对比 模型名称架构类型核心特点ImageNet Top-1准确率参数量(百万)计算效率典型应用场景ResNetCNN残差连接解决梯度…...

uniapp使用Canvas生成电子名片
uniapp使用Canvas生成电子名片 工作中有生成电子名片的一个需求,刚刚好弄了发一下分享分享 文章目录 uniapp使用Canvas生成电子名片前言一、上代码?总结 前言 先看效果 一、上代码? 不对不对应该是上才艺,哈哈哈 <template…...

世冠科技亮相中汽中心科技周MBDE会议,共探汽车研发数字化转型新路径
近日,中汽中心2025年科技周MBDE前沿应用主题会议在天津成功举办。本次会议以“智汇津门共探MBDE前沿应用新征程”为主题,聚焦基于模型的数字工程(MBDE)方法论在汽车复杂系统研发中的创新实践与跨领域协同,旨在推动行业…...

Linux笔记---线程
1. 线程的介绍 1.1 线程的概念 基本定义: 线程(Thread)是操作系统能够进行运算调度的最小单位。它被包含在进程(Process)之中(或者说是进程的一部分、对进程的划分),是进程中的实际…...

MCP架构深度解析:从基础原理到核心设计
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 持续学习,不断…...

【监控】pushgateway中间服务组件
Pushgateway 是 Prometheus 生态中的一个中间服务组件,以独立工具形式存在,主要用于解决 Prometheus 无法直接获取监控指标的场景,弥补其定时拉取(pull)模式的不足。 其用途如下: 突破网络限制࿱…...

数据库暴露--Get型注入攻击
1.背景知识 1.1Post、Get的对比 特性GET 方法POST 方法HTTP 方法类型GETPOST数据位置URL 查询字符串(?key=value)请求体(Request Body)数据可见性明文显示在 URL 和浏览器历史中不可见(除非开发者工具查看)数据长度限制受 URL 长度限制(通常约 2048 字符)无明确限制(…...
