Leetcode 2819. 购买巧克力后的最小相对损失
1.题目基本信息
1.1.题目描述
现给定一个整数数组 prices,表示巧克力的价格;以及一个二维整数数组 queries,其中 queries[i] = [ki, mi]。
Alice 和 Bob 去买巧克力,Alice 提出了一种付款方式,而 Bob 同意了。
对于每个 queries[i] ,它的条件如下:
-
如果一块巧克力的价格 小于等于 ki,那么 Bob 为它付款。
-
否则,Bob 为其中 ki 部分付款,而 Alice 为 剩余 部分付款。
Bob 想要选择 恰好 mi 块巧克力,使得他的 相对损失最小 。更具体地说,如果总共 Alice 付款了 ai,Bob 付款了 bi,那么 Bob 希望最小化 bi - ai。
返回一个整数数组 ans,其中 ans[i] 是 Bob 在 queries[i] 中可能的 最小相对损失 。
1.2.题目地址
https://leetcode.cn/problems/minimum-relative-loss-after-buying-chocolates/description/
2.解题方法
2.1.解题思路
滑动窗口+二分查找
2.2.解题步骤
第一步,记n=len(prices),将prices升序排列
第二步,枚举每一个queries[i]=[k,m]
-
2.1.构建losses数组,如果prices[i]<=k,losses[i]=prices[i];如果prices[i]>k,losses[i]=k-(prices[i]-k)=2*k-prices[i];并求losses数组的前缀和数组lossPreSums,则可以在O(1)时间内查询到子数组的和
-
2.2.证明:由prices递增可知,losses一定是先非严格递增后非严格递减,那么要让总损失最小,只能取larr1=losses[0,1,...,x]和larr2=losses[n-m+x+1,...,n-1],此时的损失f(x)=sum(larr1)+sum(larr2)=sum(prices[0,...,x])+sum([2k-prices[i] for i in [x+n-m+1,...,n-1]]),则f(x+1)-f(x)=prices[x]+prices[x+n-m+1]-2k,可知f(x)是先递减后递增的;那么对于中间长度为n-m的滑动窗口的和val=sum(losses[x+1,...,x+n-m])就是先递增后递减的,只要找到val的最大值,就找到了最小损失值
3.解题代码
python代码
from bisect import bisect_leftclass Solution:def minimumRelativeLosses(self, prices: List[int], queries: List[List[int]]) -> List[int]:# 思路1:滑动窗口+二分查找# 第一步,记n=len(prices),将prices升序排列;并前缀和数组,preSums[i]为前i项的前缀和n = len(prices)preSums = [0]prices.sort()for i in range(n):preSums.append(preSums[-1] + prices[i])# print("preSums", preSums)# 第二步,枚举每一个queries[i]=[k,m]result = []for k, m in queries:# 2.1.证明:由prices递增可知,losses一定是先非严格递增后非严格递减,那么要让总损失最小,只能取larr1=losses[0,1,...,x]和larr2=losses[n-m+x+1,...,n-1],此时的损失f(x)=sum(larr1)+sum(larr2)=sum(prices[0,...,x])+sum([2k-prices[i] for i in [x+n-m+1,...,n-1]]),则f(x+1)-f(x)=prices[x]+prices[x+n-m+1]-2k,可知f(x)是先递减后递增的;那么对于中间长度为n-m的滑动窗口的和val=sum(losses[x+1,...,x+n-m])就是先递增后递减的,只要找到val的最大值,就找到了最小损失值# 2.2.找到第一个price大于等于k的索引位置,记为p1p1 = bisect_left(prices, k)# print("p1", p1)# 2.3.从[0,...,p1]中找到第一个index,记index2=index+(n-m),使prices[index]>=2*k-prices[index2]。红蓝染色不变量:prices[left-1]<2*k-prices[index2]恒成立,最终的left即为要找的indexleft, right = 0, p1while left < right:mid = (right - left) // 2 + leftindex2 = mid + n - mif index2 < n and prices[mid] < 2 * k - prices[index2]:left = mid + 1else:right = midindex = left# print("left, right", left, right)# 2.4.根据index求最小损失,minLoss=sum(prices[0,...,index-1])+sum([2*k-prices[j] for j in [index+n-m,...,n-1]])val = preSums[index] + 2 * k * (m - index) - (preSums[n] - preSums[index + n - m])result.append(val)return result
4.执行结果

相关文章:

Leetcode 2819. 购买巧克力后的最小相对损失
1.题目基本信息 1.1.题目描述 现给定一个整数数组 prices,表示巧克力的价格;以及一个二维整数数组 queries,其中 queries[i] [ki, mi]。 Alice 和 Bob 去买巧克力,Alice 提出了一种付款方式,而 Bob 同意了。 对于…...

AI炼丹日志-25 - OpenAI 开源的编码助手 Codex 上手指南
点一下关注吧!!!非常感谢!!持续更新!!! Java篇: MyBatis 更新完毕目前开始更新 Spring,一起深入浅出! 大数据篇 300: Hadoop&…...

AnyConv OGG 转换器:轻松转换音频格式
在数字音频世界中,不同的文件格式适用于不同的场景和设备。OGG 是一种开放、免费的音频格式,具有高压缩率和良好的音质。然而,有时我们需要将 OGG 文件转换为其他格式,或者将其他格式转换为 OGG。这就是 AnyConv OGG 转换器发挥作用的地方。 什么是 AnyConv OGG 转换器? …...

C# 类和继承(使用基类的引用)
使用基类的引用 派生类的实例由基类的实例和派生类新增的成员组成。派生类的引用指向整个类对象,包括 基类部分。 如果有一个派生类对象的引用,就可以获取该对象基类部分的引用(使用类型转换运算符把 该引用转换为基类类型)。类…...

进程间通信(消息队列)
目录 一 原理 二 API 1. ftok 2. msgget 3. msgctl 4. msgsnd 5. msgrcv 三 demo代码 四 基于责任链模式和消息队列对数据处理 1. 什么是责任链模式 2. 下面基于责任链模式来对消息队列获取的消息进行处理 前置 其实system v 版本的进程间通信,设计的接…...

Linux gron 命令使用详解
简介 gron 是一个独特的命令行工具,用于将 JSON 数据转换为离散的、易于 grep 处理的赋值语句格式。它的名字来源于 “grepable on” 或 “grepable JSON”,主要解决在命令行中处理复杂 JSON 数据的难题。 核心价值 gron 的核心是将 JSON 数据展平为类…...

Nginx--手写脚本压缩和切分日志(也适用于docker)
原文网址:Nginx--手写脚本压缩和切分日志(也适用于docker)_IT利刃出鞘的博客-CSDN博客 简介 本文介绍nginx如何手写脚本压缩和切分日志。 1.创建切分日志的脚本 创建脚本文件:/work/tmp/nginx-log_sh(后边要用run-…...

OpenCv高阶(十八)——dlib人脸检测与识别
文章目录 一、dlib库是什么?二、opencv库与dlib库的优缺点对比1、opencv优缺点2、dlib库优缺点 三、dlib库的安装1、在线安装2、本地安装 四、dlib库的人脸检测器1. 基于 HOG 的检测器2. 基于 CNN 的检测器 五、dlib人脸检测的简单使用1、导入必要库2、初始化人脸检…...

中山大学无人机具身导航新突破!FlightGPT:迈向通用性和可解释性的无人机视觉语言导航
作者:Hengxing Cai 1 , 2 ^{1,2} 1,2, Jinhan Dong 2 , 3 ^{2,3} 2,3, Jingjun Tan 1 ^{1} 1, Jingcheng Deng 4 ^{4} 4, Sihang Li 2 ^{2} 2, Zhifeng Gao 2 ^{2} 2, Haidong Wang 1 ^{1} 1, Zicheng Su 5 ^{5} 5, Agachai Sumalee 6 ^{6} 6, Renxin Zhong 1 ^{1} …...
WIN11+CUDA11.8+VS2019配置BundleFusion
参考: BundleFusion:VS2019 2017 ,CUDA11.5,win11,Realsense D435i离线数据包跑通,环境搭建 - 知乎 Win10VS2017CUDA10.1环境下配置BundleFusion - 知乎 BundleFusionWIN11VS2019 CUDA11.7环境配置-CSDN博客 我的环境:Win 11…...
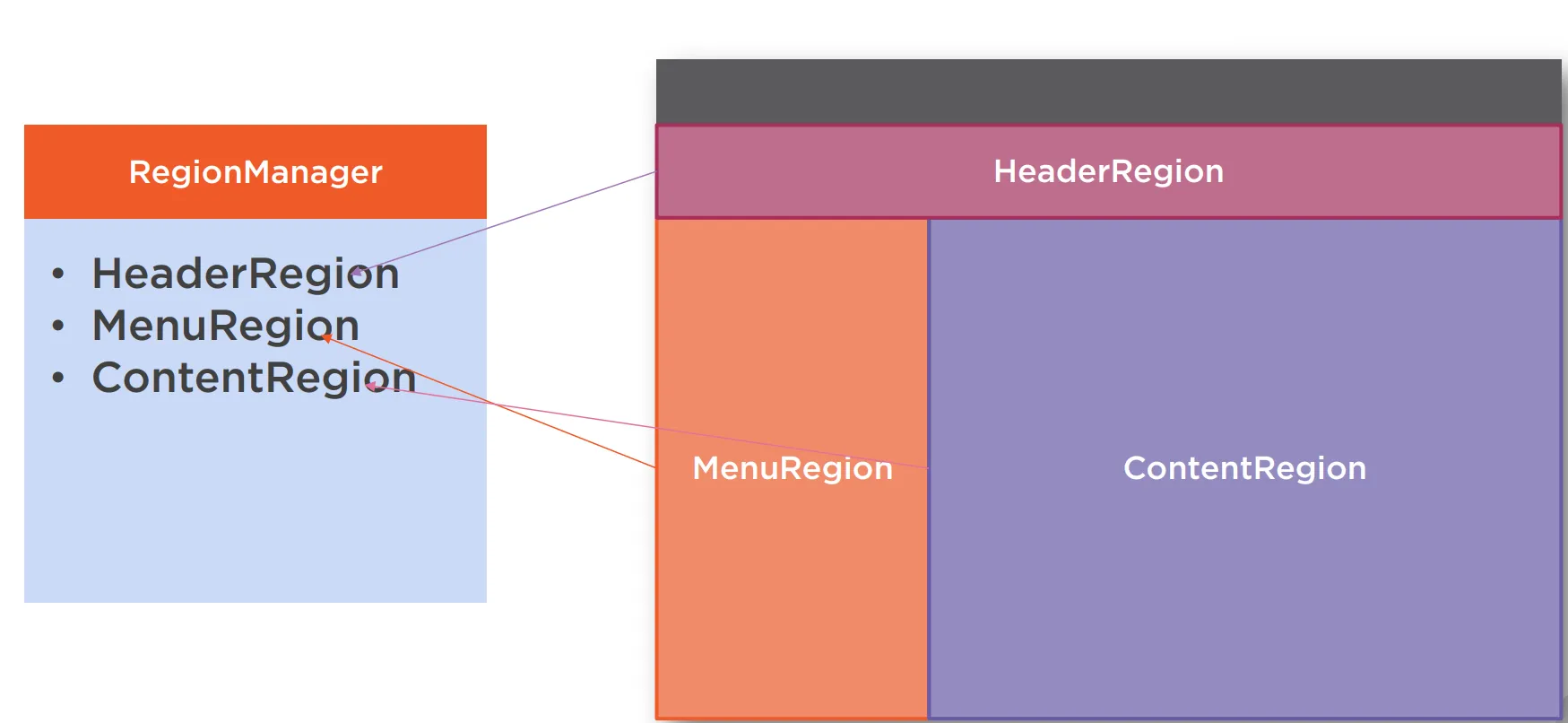
WPF prism
Prism Prism.Dryloc 包 安装 Nuget 包 - Prism.DryIoc 1. 修改 App.xaml 修改 App.xaml 文件,添加 prism 命名空间, 继承由 Application → PrismApplication,删除默认启动 url, StartupUri“MainWindow.xaml” <dryioc:PrismApplicationx:Class…...

实时同步缓存,与阶段性同步缓存——补充理解《补充》
根据 Redis 缓存的数据与 DBMS 中数据的同步性划分,缓存一般可划分为两类:实时同步缓存,与阶段性同步缓存。 实时同步缓存是指,DBMS 中数据更新后,Redis 缓存中的存放的相关数据会被立即清 除,以促使再有对…...

[Redis] Redis:高性能内存数据库与分布式架构设计
标题:[Redis] 浅谈分布式系统 水墨不写bug 文章目录 一、什么是Redis?一、核心定位二、核心优势三、典型应用场景四、Redis vs 传统数据库 二、架构选择与设计1、单机架构(应用程序 数据库服务器)2、应用程序和数据库服务器分离3…...

Mobaxterm解锁Docker
Mobaxterm是一款功能强大的终端模拟器和SSH客户端,它支持Windows、Linux和Mac操作系统,对于使用Docker的开发者和运维人员来说,Mobaxterm是一个非常有用的工具。本文将深入解析Mobaxterm,并分享一些使用Docker时的高效技巧。 Mob…...

React 第四十九节 Router中useNavigation的具体使用详解及注意事项
前言 useNavigation 是 React Router 中一个强大的钩子,用于获取当前页面导航的状态信息。 它可以帮助开发者根据导航状态优化用户体验,如显示加载指示器、防止重复提交等。 一、useNavigation核心用途 检测导航状态:判断当前是否正在进行…...

【JavaEE】Spring事务
目录 一、事务简介二、Spring事务的实现2.1 事务的操作2.2 分类2.2.1 Spring编程式事务2.2.2 Spring 声明式事务 Transactional2.2.2.1 Transactional 详解2.2.2.1.1 rollbackFor2.2.2.1.2 Isolation2.2.2.1.3 propagation 一、事务简介 事务:事务是⼀组操作的集合…...

Flink 状态管理深度解析:类型与后端的全面探索
在流处理场景中,数据往往是连续且无界的,为了准确处理这些数据并维持计算的连续性,Flink 引入了状态管理机制。Flink 的状态管理包含状态类型和状态后端两大部分,它们相辅相成,共同为作业的可靠性、容错性和性能提供保障。接下来,我们将深入探究 Flink 状态管理中状态类型…...

Android15 userdebug版本不能remount
背景描述: 最近调试Android Vendor Hal的时候发现一个奇怪的现象: android userdebug版本刷到设备中,执行adb root没提示错误,但是没有获取到root权限。 Android设备运行的系统版本有三种情况:user版本、userdebug版本和eng版本…...

R包安装报错解决案例系列|R包使用及ARM架构解决data.table安装错误问题
有不少同学是Mac系统的,分析过程中会发现部分R包总是安装不成功,这是因为部分R包基于windowsx86架构编译的,最常见的就是含 C/C/Fortran 的包,对于初学者都是建议linux和win去做,Windows 通常直接安装预编译好的二进制…...

k8s Headless Service
Kubernetes 无头服务(Headless Service)配置与使用场景 1.无头服务概述 无头服务(Headless Service)是 Kubernetes 中的一种特殊服务类型,它**不分配集群 IP(ClusterIP),而是直接暴露…...

Linux上安装MongoDB
目录 一、在Linux系统安装MongoDB服务器 1、下载MongoDB 2、上传MongoDB并解压 3、创建必要目录 4、配置环境变量 5、创建配置文件 6、启动命令 7、验证安装 二、在Linux系统安装MongoDB客户端Shell 1、下载MongoDB Shell 2、上传MongoDB Shell并解压 3、配置环境变…...

Redis最佳实践——安全与稳定性保障之访问控制详解
Redis 在电商应用的安全与稳定性保障之访问控制全面详解 一、安全访问控制体系架构 1. 多层级防护体系 #mermaid-svg-jpkDj2nKxCq9AXIW {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-jpkDj2nKxCq9AXIW .error-ico…...

【华为开发者空间 x DeepSeek】服务器运行Ollama并在本地调用
文章概述 本文介绍了如何在 华为开发者空间 中快速部署并使用 Ollama 模型运行框架,并结合 deepseek-r1 模型进行本地或远程交互推理。内容涵盖环境准备、模型配置、网卡绑定、内网穿透、API调用等多个环节,适合希望在华为云上快速搭建本地类大模型推理…...

Halcon
regiongrowing — Segment an image using regiongrowing. get_obj_class:获取图像的类别名 get_region_points:获取区域的像素 get_contour_xld:获取xld像素点坐标 get_polygon_xld:获取多边形的数据 get_region_polygon:计算一个区域的…...

STM32之IIC(重点)和OLED屏
内部集成电路概述 基本概念 内部集成电路(Inter Integrated Circuit)的简称叫做IIC或者I2C,是一种简单的、半双工同步通信的串行通信接口,IIC总线是上世纪80年代(1982年)由飞利浦公司设计出来,…...

学习海康VisionMaster之表面缺陷滤波
一:进一步学习了 今天学习下VisionMaster中的表面缺陷滤波:简单、无纹理背景的表面缺陷检测,可以检测表面的异物,缺陷,划伤等 二:开始学习 1:什么表面缺陷滤波? 表面缺陷滤波的核心…...

游戏引擎学习第314天:将精灵拆分成多个层
回顾并为今天的工作做准备 我们今天继续昨天开始的工作,现在我们要回到渲染中处理 Z 值的最终环节。我们目前已经有一个我们认为还算合理的排序方式,虽然可能还需要在接下来的过程中进行一些调整,但总体上已经有了一个明确的方向。 我们已经…...

【学习笔记】深度学习-梯度概念
一、定义 梯度向量不仅表示函数变化的速度,还表示函数增长最快的方向 二、【问】为什么说它表示方向? 三、【问】那在深度学习梯度下降的时候,还要判断梯度是正是负来更新参数吗? 假设某个参数是 w,损失函数对它的…...

【数据结构】图的存储(邻接矩阵与邻接表)
图的存储结构 因为图中既有节点,又有边(节点与节点之间的关系),因此,在图的存储中,只需要保存:节点和边关系即可。 节点保存比较简单,只需要一段连续空间即可,那边关系该怎么保存呢࿱…...

tomcat yum安装
使用yum安装 yum install -y java-1.7.0-openjdk* tomcat* --disablerepoepel## java-1.7.0-openjdk* 注意:最终安装的是java-1.8.0版本## --disablerepoepel 禁用:EPEL源,防止版本冲突 java -version (2) 启停:Tomcat 7 s…...
