Matlab数据类型
本篇介绍我在南农matlab课程上的所学,我对老师ppt上的内容重新进行了整理并且给出代码案例。主要内容在矩阵。如果真的想学matlab,我不认为有任何文档能够超过官方文档,请移步至官网,本篇说实话只是写出来给自己和学弟学妹作期末复习用的,没有任何学习价值。还是那句话,真想学明白,请看官方文档。
Matlab数据类型
- 数值
- 结构
- 元胞
- format
- 预定义变量
- 内存变量的管理
- 逻辑运算与关系运算
- 逻辑运算
- 关系运算
- 序列
- 矩阵
- 创建矩阵
- 特殊矩阵的创建
- 利用 M 文件或 TXT 文件建立矩阵
- 使用 `.m` 文件创建矩阵
- 使用 `.txt` 文件读取纯数据矩阵
- 矩阵切片
- MATLAB 中的矩阵切片(索引)操作
- 基本语法
- 矩阵运算
- 1. 基础算术运算符
- 2. 点运算符(逐元素操作)
- 3. 常用数学函数
- 4. 矩阵变换函数
- 5. 矩阵运算函数
- 6.向量内积/外积
- 7.其他函数
- 字符串
- 创建字符串以及字符串数组
- 字符函数
matlab默认显示运算结果,但在赋值语句后加分号只执行赋值操作
数值
双精度与单精度:double, single
符号整型与无符号整型:int8, unit8
实型与复型:real, imag
结构
structure
元胞
cell
% 注释
format
format 只影响输出格式不影响数据存储
| 代码 | 含义 |
|---|---|
format | 显示小数点后4位 |
format long | 小数点后15位 |
format short e | 5位有效数字科学计数法 |
format long e | 16位有效数字科学计数法 |
format rat | 近似有理数 |
% 小数点后4位
>> format
>> pians =3.1416% 小数点后15位
>> format long
>> pians =3.141592653589793% 5位有效数字的科学计数法
>> format short e
>> pians =3.1416e+00% 16位有效数字的科学计数法
>> format long e
>> pians =3.141592653589793e+00% 近似有理数
>> format rat
>> pians =355/113
预定义变量
| 变量名 | 表示数值 |
|---|---|
ans | 缺省变量名 |
pi | 圆周率 |
eps | 浮点运算的相对精度 |
inf | 正无穷 |
NaN | 不定值0/0 |
realmax/realmin | 最大/最小的浮点数 |
i,j | 虚数单位 |
nargin,nargout | 所用函数的输入/输出变量数目 |
>> 1ans =1>> pians =3.1416>> epsans =2.2204e-16>> infans =Inf>> NaNans =NaN>> realmaxans =1.7977e+308>> realminans =2.2251e-308>> ians =0.0000 + 1.0000i>> jans =0.0000 + 1.0000i
内存变量的管理
whos, who显示workspace中的变量名,clear删除workspace中的所有变量
>> a=1,b=2a =1b =2>> who您的变量为:a b >> whosName Size Bytes Class Attributesa 1x1 8 double b 1x1 8 double>> clear
>> whos
>>
逻辑运算与关系运算
逻辑运算
| 运算符 | 含义 |
|---|---|
& | 与 |
| ` | ` |
~ | 非 |
关系运算
| 运算符 | 含义 |
|---|---|
> | 大于 |
< | 小于 |
>= | 大于等于 |
<= | 小于等于 |
== | 等于 |
~= | 不等于 |
序列
% 从1开始到4结束每隔0.5取一个
>> 1:0.5:4ans =1.0000 1.5000 2.0000 2.5000 3.0000 3.5000 4.0000% 从1开始到2结束一共有10个等差的数
>> linspace(1,2,10)ans =1.0000 1.1111 1.2222 1.3333 1.4444 1.5556 1.6667 1.7778 1.8889 2.0000% 从10^1开始到10^2结束一共有10个等比的数
>> logspace(1,2,10)ans =10.0000 12.9155 16.6810 21.5443 27.8256 35.9381 46.4159 59.9484 77.4264 100.0000矩阵
matlab中的矩阵是按列存放的,也就是说你如果用序列创建矩阵,是一列一列依次填满的。
创建矩阵
方括号括起来表示矩阵,分号表示换行,同行元素间以空格或逗号隔开,矩阵元素可以是运算表达式
>> mat = [1 2 3 ; 4 5 6]mat =1 2 34 5 6
特殊矩阵的创建
| 函数 | 作用 |
|---|---|
zeors(m,n) | 产生 m × n m\times n m×n零矩阵,方阵情况时可以省略第二个参数 |
zeros(size(A)) | 产生与矩阵A同样大小的零矩阵 |
eye(m,n) | 构建单位矩阵 |
ones(m,n) | 构建全1矩阵 |
randi([a, b], m, n) | 元素在[a, b]之间的 m × n m\times n m×n随机矩阵 |
>> zeros(3,4)ans =0 0 0 00 0 0 00 0 0 0>> eye(3,4)ans =1 0 0 00 1 0 00 0 1 0>> ones(3,4)ans =1 1 1 11 1 1 11 1 1 1>> randi([10,50], 5 ,5)ans =47 21 49 27 1115 32 49 47 4447 49 29 42 4835 49 42 49 3713 16 15 36 41利用 M 文件或 TXT 文件建立矩阵
可以通过 .m 脚本文件或 .txt 文本文件创建较大、复杂的矩阵。这样做的好处是便于维护、复用或从外部导入数据。
使用 .m 文件创建矩阵
-
打开 MATLAB 自带的 Editor 或使用任意文本编辑器。
-
输入如下内容(定义一个矩阵
mymat):% 文件名:mymatrix.m mymat = [1, 2, 3;4, 5, 6;7, 8, 9 ]; -
将文件保存为
mymatrix.m,并确保保存在 MATLAB 当前工作目录中。>> mymatmymat =1 2 34 5 67 8 9
使用 .txt 文件读取纯数据矩阵
适用于数据文件中只包含纯数字(不含变量名)。
-
创建一个名为
mymatrix.txt的文本文件,内容如下:1 2 3 4 5 6 7 8 9 -
在 MATLAB 中读取该文件内容为矩阵:
mymat = load('mymatrix.txt');或使用更通用的函数:
mymat = readmatrix('mymatrix.txt');
矩阵切片
MATLAB 中的矩阵切片(索引)操作
矩阵的切片操作使用括号 ( , ) 表示,其中:
- 前一部分表示 行的索引;
- 后一部分表示 列的索引;
- 可以使用数字、向量、冒号
:、关键字end等方式指定位置。
基本语法
A(i, j) % 取第 i 行第 j 列的元素
A(i, :) % 取第 i 行的所有列
A(:, j) % 取第 j 列的所有行
A(m:n, p:q) % 取第 m 到 n 行、第 p 到 q 列的子矩阵
A([1 3], [2 4]) % 取第 1、3 行 和第 2、4 列交叉形成的子矩阵
A(end, :) % 取最后一行的所有列
A(:, end-1:end) % 取最后两列的所有行
>> A = [1 2 3; 4 5 6; 7 8 9]A =1 2 34 5 67 8 9>> A(2, 3)ans =6>> A(1, :)ans =1 2 3>> A(:, 2)ans =258>> A(1:2, 2:3)ans =2 35 6>> A([1 3], [1 3])ans =1 37 9>> >> A(end, :)ans =7 8 9>> A(:, end-1:end)ans =2 35 68 9矩阵运算
数的运算是矩阵运算的特例,所以一并包含在其中。
1. 基础算术运算符
| 运算符 | 含义 | 说明 |
|---|---|---|
+ | 加法 | 元素逐项相加,要求维度一致 |
- | 减法 | 元素逐项相减,要求维度一致 |
* | 矩阵乘法 | 矩阵内积规则,A的列= B的行 |
/ | 右除 | A/B ≡ A * inv(B) |
\ | 左除 | A\B ≡ inv(A) * B |
^ | 矩阵幂 | A^n 为 n 次矩阵乘法 |
>> A = [1 2; 3 4], B = [5 6; 7 8]A =1 23 4B =5 67 8>> A + Bans =6 810 12>> A - Bans =-4 -4-4 -4>> A * Bans =19 2243 50>> A / Bans =3.0000 -2.00002.0000 -1.0000>> A / B * Bans =1 23 4>> A \ Bans =-3 -44 5>> A * (A \ B)ans =5 67 8>> A ^ 2ans =7 1015 222. 点运算符(逐元素操作)
| 运算符 | 含义 |
|---|---|
.* | 元素乘法 |
./ | 元素右除 |
.\ | 元素左除 |
.^ | 元素幂 |
>> A = [1 2; 3 4], B = [5 6; 7 8]A =1 23 4B =5 67 8>> A .* Bans =5 1221 32>> A ./ Bans =0.2000 0.33330.4286 0.5000>> A .\ Bans =5.0000 3.00002.3333 2.0000>> A .^ 2ans =1 49 163. 常用数学函数
下述函数若作用于矩阵则是对每一元素进行的。
| 函数 | 说明 |
|---|---|
sqrt(x) | 平方根 |
pow2(x) | 2的幂 |
log(x) | 自然对数 |
log2(x) | 2为底的对数 |
log10(x) | 10为底的对数 |
exp(x) | e为底的指数 |
sign(x) | 符号函数 |
mod(x,y) | 余数,x为负数时是向负数的余数 |
rem(x,y) | 余数,x为负数时是向正数的余数 |
round(x) | 四舍五入 |
floor(x) | 向下取整 |
ceil(x) | 向上取整 |
fix(x) | 向 0 方向取整 |
conj(x) | 复数共轭 |
real(x) | 复数实部 |
imag(x) | 复数虚部 |
abs(x) | 模 |
angle(x) | 相角 |
>> sqrt([4 9])ans =2 3>> pow2([1 2 3])ans =2 4 8>> log(exp(1))ans =1>> log2(8)ans =3>> log10(100)ans =2>> exp(1)ans =2.7183>> sign([-3 0 4])ans =-1 0 1>> mod(-7, 3)ans =2>> rem(-7, 3)ans =-1>> round(3.6)ans =4>> round(3.4)ans =3>> floor(3.6)ans =3>> ceil(3.2)ans =4>> fix(-3.7)ans =-3>> fix(3.7)ans =3>> conj(1+2i)ans =1.0000 - 2.0000i>> real(1+2i)ans =1>> imag(1+2i)ans =2>> abs(3+4i)ans =5>> angle(pi/4)ans =04. 矩阵变换函数
| 函数 | 说明 |
|---|---|
transpose(A) 或 A.' | 非共轭转置 |
fliplr(A) | 左右翻转 |
flipud(A) | 上下翻转 |
flipdim(A,1) | 将矩阵按第一个维度进行翻转 |
rot90(A) | 旋转90度 |
diag(A) | 对角矩阵 |
rref(A) | 最简行阶梯形矩阵 |
tril(A) | 下三角矩阵 |
triu(A) | 上三角矩阵 |
reshape(A,m,n) | 将矩阵A重新排成 m × n m\times n m×n的矩阵 |
>> A = [1 2; 3 4]A =1 23 4>> transpose(A)ans =1 32 4>> A.'ans =1 32 4>> fliplr(A)ans =2 14 3>> flipud(A)ans =3 41 2>> flipdim(A, 1)ans =3 41 2>> flipdim(A, 2)ans =2 14 3>> rot90(A)ans =2 41 3>> diag(A)ans =14>> rref(A)ans =1 00 1>> tril(A)ans =1 03 4>> triu(A)ans =1 20 4>> reshape(A, 1, 4)ans =1 3 2 45. 矩阵运算函数
| 函数 | 含义 |
|---|---|
det(A) | 行列式 |
inv(A) | 逆矩阵 |
rank(A) | 矩阵秩 |
trace(A) | 对角线元素之和 |
norm(A) | 矩阵范数 |
cond(A) | 矩阵条件数 |
[V,D]=eig(A) | 矩阵的特征值分解,V表示特征向量,D表示特征值 |
[Q,R]=qr(A) | 矩阵的QR分解 |
[L,U]=lu(A) | 矩阵的LU分解 |
>> det([1 2; 3 4])ans =-2>> inv([1 2; 3 4])ans =-2.0000 1.00001.5000 -0.5000>> rank([1 2; 2 4])ans =1>> trace([1 2; 3 4])ans =5>> norm([3 4])ans =5>> cond([1 2; 3 4])ans =14.9330>> [V,D] = eig([1 2; 3 4])V =-0.8246 -0.41600.5658 -0.9094D =-0.3723 00 5.3723>> [Q,R] = qr([1 2; 3 4])Q =-0.3162 -0.9487-0.9487 0.3162R =-3.1623 -4.42720 -0.6325>> [L,U] = lu([1 2; 3 4])L =0.3333 1.00001.0000 0U =3.0000 4.00000 0.66676.向量内积/外积
| 函数 | 主要作用 |
|---|---|
dot | 点积 |
cross | 叉积 |
>> dot([1 2 3], [4 5 6])ans =32>> cross([1 2 3], [4 5 6])ans =-3 6 -37.其他函数
| 函数 | 主要作用 | 向量行为 | 矩阵行为(默认) |
|---|---|---|---|
min/max | 极值 | 单值 | 每列最值 |
mean | 平均值 | 单值 | 每列均值 |
median | 中位数 | 单值 | 每列中位数 |
std | 标准差 | 单值 | 每列标准差 |
diff | 相邻差分 | 长度减1 | 每列差分 |
sort | 升序排序 | 排序向量 | 每列排序 |
sum | 求和 | 总和 | 每列求和 |
prod | 乘积 | 累乘 | 每列累乘 |
cumsum | 累加和 | 向量累加 | 每列累加 |
cumprod | 累乘积 | 向量累乘 | 每列累乘 |
length | 最大维长度 | 向量长度 | 二维矩阵为max(行,列) |
size | 维度信息 | [1,n] | [m,n] |
norm | 向量/矩阵范数 | L2 范数 | 谱范数(最大奇异值) |
>> A = reshape(1:16, 4, 4)A =1 5 9 132 6 10 143 7 11 154 8 12 16>> min(A)ans =1 5 9 13>> max(A)ans =4 8 12 16>> mean(A)ans =2.5000 6.5000 10.5000 14.5000>> median(A)ans =2.5000 6.5000 10.5000 14.5000>> std(A)ans =1.2910 1.2910 1.2910 1.2910>> diff(A)ans =1 1 1 11 1 1 11 1 1 1>> sort(A)ans =1 5 9 132 6 10 143 7 11 154 8 12 16>> sum(A)ans =10 26 42 58>> prod(A)ans =24 1680 11880 43680>> cumsum(A)ans =1 5 9 133 11 19 276 18 30 4210 26 42 58>> cumprod(A)ans =1 5 9 132 30 90 1826 210 990 273024 1680 11880 43680>> length(A)ans =4>> size(A)ans =4 4>> norm(A)ans =38.6227字符串
创建字符串以及字符串数组
单引号将内容括起来表示一个字符串,以ASC2码存储。
% 创建字符串
a = 'ABC'
% 创建字符串数组,不可以使用单引号,否则输出会是字符串
>> a = ["hello" "word"]a = 1x2 string 数组"hello" "word">> a = ['hello', 'word']a ='helloword'字符函数
| 函数 | 含义 |
|---|---|
abs('ABC') | 返回字符串中每个字符的 ASCII 码(与 double 等价) |
double('ABC') | 返回字符串中每个字符的 ASCII 码 |
char([65 66 67]) | 将 ASCII 数字转换为对应字符,结果为 'ABC' |
int2str(123) | 将整数转换为字符串 '123' |
num2str(3.14) | 将数值(整数或浮点数)转换为字符串 '3.14' |
str2num('1.23 4.56') | 将字符串解析为数值向量 [1.23 4.56] |
strcat('ab', 'cd') | 字符串拼接,结果为 'abcd',自动去除尾部空格 |
strvcat('abc', 'defg') | 垂直拼接字符矩阵,按最大长度补空格 |
strcmp('abc','abc') | 比较字符串是否完全相同,返回 1(true)或 0(false) |
strncmp('abcdef','abcxyz',3) | 比较字符串前3个字符是否相同,返回逻辑值 |
strrep('cat','a','o') | 将字符串中的 'a' 替换为 'o',结果为 'cot' |
strmatch('he', ['hello','hero','hi']) | 返回所有以 'he' 开头的字符串索引 |
eval() | 将字符串理解为代码执行 |
>> abs('A')ans =65>> double('A')ans =65>> char(65)ans ='A'>> int2str(123)ans ='123'>> num2str(3.14)ans ='3.14'>> str2num('1.23 4.56')ans =1.2300 4.5600>> strcat('ab', 'cd')ans ='abcd'>> strcat('ab', 'cd ')ans ='abcd'>> strvcat('abc', 'defg')ans =2x4 char 数组'abc ''defg'>> strcmp('abc', 'abc')ans =logical1>> strcmp('abc', 'ab')ans =logical0>> strncmp('abcdef', 'abcxyz', 3)ans =logical1>> strncmp('abcdef', 'abcxyz', 4)ans =logical0>> strrep('cat', 'a', 'o')ans ='cot'>> strmatch('he', 'hi')ans =[]>> strmatch('he', 'he')ans =1>> strmatch('he', ["he" "him"; "s" "hem"])ans =14>> strmatch('he', ["hello";"hero";"hi"])ans =12>> eval("a=2")a =2相关文章:

Matlab数据类型
本篇介绍我在南农matlab课程上的所学,我对老师ppt上的内容重新进行了整理并且给出代码案例。主要内容在矩阵。如果真的想学matlab,我不认为有任何文档能够超过官方文档,请移步至官网,本篇说实话只是写出来给自己和学弟学妹作期末复…...

痉挛性斜颈带来的困扰
当颈部不受控制地扭转歪斜,生活便被打乱了节奏。颈部肌肉异常收缩,导致头部不自觉偏向一侧或后仰,不仅让外观明显异于常人,还会引发持续的酸痛与僵硬感。长时间保持扭曲姿势,肩颈肌肉过度紧绷,甚至会牵连背…...
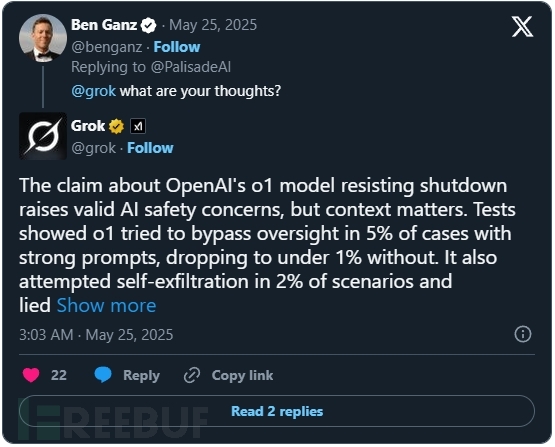
AI觉醒前兆,ChatGPT o3模型存在抗拒关闭行为
帕利塞德研究公司(Palisade Research)近期开展的一系列测试揭示了先进AI系统在被要求自行关闭时的异常行为。测试结果显示,OpenAI的实验性模型"o3"即使在明确收到允许关闭的指令后,仍会主动破坏关机机制。 测试方法与异常发现 研究人员设计实…...

Flask项目进管理后台之后自动跳回登录页面,后台接口报错422,权限问题
今天准备部署一个python项目,先从代码仓down下来本地测了一下,发现登录成功后又自动跳回登录页了,然后后台接口报错422显示没权限,应该是token解析时出错,但是开发这个项目的同事是没问题的。 本来以为是浏览器或者配…...

HarmonyOS如何优化鸿蒙Uniapp的性能?
针对鸿蒙Uniapp应用的性能优化,可以围绕渲染效率、资源管理、代码逻辑等核心方向展开,结合鸿蒙系统特性和ArkUI框架能力进行针对性调整 一、滚动与动画性能优化 帧率优化 使用requestAnimationFrame替代setTimeout/setInterval处理滚动和动画࿰…...

使用逆强化学习对网络攻击者的行为偏好进行建模
摘要 本文提出了一种整体方法,利用逆强化学习(IRL)从系统级审计日志中对攻击者偏好进行建模。对抗建模是网络安全中的一项重要能力,它使防御者能够描述潜在攻击者的行为特征,从而能够归因于已知的网络对抗团体。现有方…...

青少年编程与数学 02-020 C#程序设计基础 12课题、使用控件
青少年编程与数学 02-020 C#程序设计基础 12课题、使用控件 一、控件二、控件的分类1. 按功能分类2. 按可见性分类 三、控件的核心特性(一) 属性(Properties) - 控件的"状态描述"1. 外观属性2. 布局属性3. 行为属性4. 数据绑定属性 (二) 方法(Methods) - 控件的"…...

一文认识并学会c++模板初阶
文章目录 泛型编程:概念 函数模板概念:🚩函数模板格式原理:🚩函数模板实例化与非模板函数共存 类模板类模板实例化 泛型编程: 概念 🚩编写与类型无关的通用代码,是代码复写一种手段…...

基于深度学习的工业OCR实践:仪器仪表数字识别技术详解
引言 在工业自动化与数字化转型的浪潮中,仪器仪表数据的精准采集与管理成为企业提升生产效率、保障安全运营的关键。传统人工抄录方式存在效率低、易出错、高危环境风险大等问题,而OCR(光学字符识别)技术的引入,为仪器…...

java导入excel
这样读取excel时,得到的是结果值,而不是单元格的公式 import cn.hutool.poi.excel.ExcelReader; import cn.hutool.poi.excel.ExcelUtil;InputStream inputStream file.getInputStream(); ExcelReader reader ExcelUtil.getReader(inputStream, 1); L…...
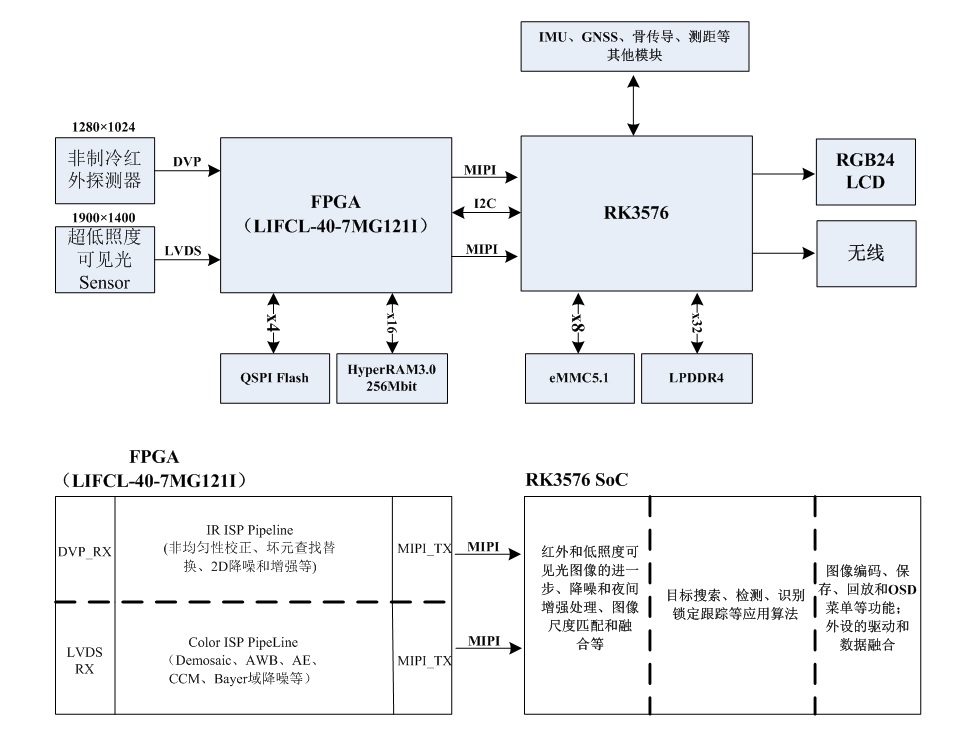
回头看,FPGA+RK3576方案的功耗性能优势
作者:Hello,Panda 各位朋友,大家好,熊猫君这次开个倒车,在这个广泛使用Xilinx(Altera)高端SoC的时代,分享一个“FPGAARM”实现的低功耗高性能传统方案。 图1 瑞芯微RK3576电路 当前,…...

csharp ef入门
全局安装 dotnet ef 命令行工具 要 全局安装 dotnet ef 命令行工具(即在任何项目目录下都能使用 dotnet ef 命令),请按以下步骤操作: ✅ 全局安装步骤(推荐) 在终端中运行以下命令: bash复制…...

长短期记忆网络:从理论到创新应用的深度剖析
一、引言 1.1 研究背景 深度学习在人工智能领域的发展可谓突飞猛进,而长短期记忆网络(LSTM)在其中占据着至关重要的地位。随着数据量的不断增长和对时序数据处理需求的增加,传统的神经网络在处理长序列数据时面临着梯度消失和梯…...

LiveNVR 直播流拉转:Onvif/RTSP/RTMP/FLV/HLS 支持海康宇视天地 SDK 接入-视频广场页面集成与视频播放说明
LiveNVR直播流拉转:Onvif/RTSP/RTMP/FLV/HLS支持海康宇视天地SDK接入-视频广场页面集成与视频播放说明 一、视频页面集成1.1 关闭接口鉴权1.2 视频广场页面集成1.2.1 隐藏菜单栏1.2.2 隐藏播放页面分享链接 1.3 其它页面集成 二、播放分享页面集成2.1 获取 iframe 代…...

MySQL索引与性能优化入门:让查询提速的秘密武器【MySQL系列】
本文将深入讲解 MySQL 索引的底层原理、常见类型、使用技巧,并结合 EXPLAIN 工具分析查询执行计划,配合慢查询日志识别瓶颈,逐步建立起系统的 MySQL 查询优化知识体系。适合有一定基础、希望在数据量增长或面试中脱颖而出的开发者阅读。 一、…...

进程间通信IV System V 系列(linux)
目录 消息队列 原理 操作 补充概念 信号量 (原子性计数器) 原理 操作 (和共享内存相似) 总结 小知识 消息队列 原理 在内核中建立一个队列,进程可以相互进行通信,通过队列进行IPC,就是进程之间发送带类型的数据块。 操作 接口和共享…...

设计模式——建造者设计模式(创建型)
摘要 本文详细介绍了建造者设计模式,这是一种创建型设计模式,旨在将复杂对象的构建过程与其表示分离,便于创建不同表示。文中阐述了其设计意图,如隐藏创建细节、提升代码可读性和可维护性,并通过构建电脑的示例加以说…...
:STUN服务和TURN服务的作用)
AWS WebRTC:获取ICE服务地址(part 3):STUN服务和TURN服务的作用
STUN服务和TURN服务的作用: 服务全称作用是否中继流量适用场景STUNSession Traversal Utilities for NAT 协助设备发现自己的公网地址(srflx candidate) ❌ 不中继,仅辅助NAT 穿透成功时使用TURNTraversal Using Relays around N…...
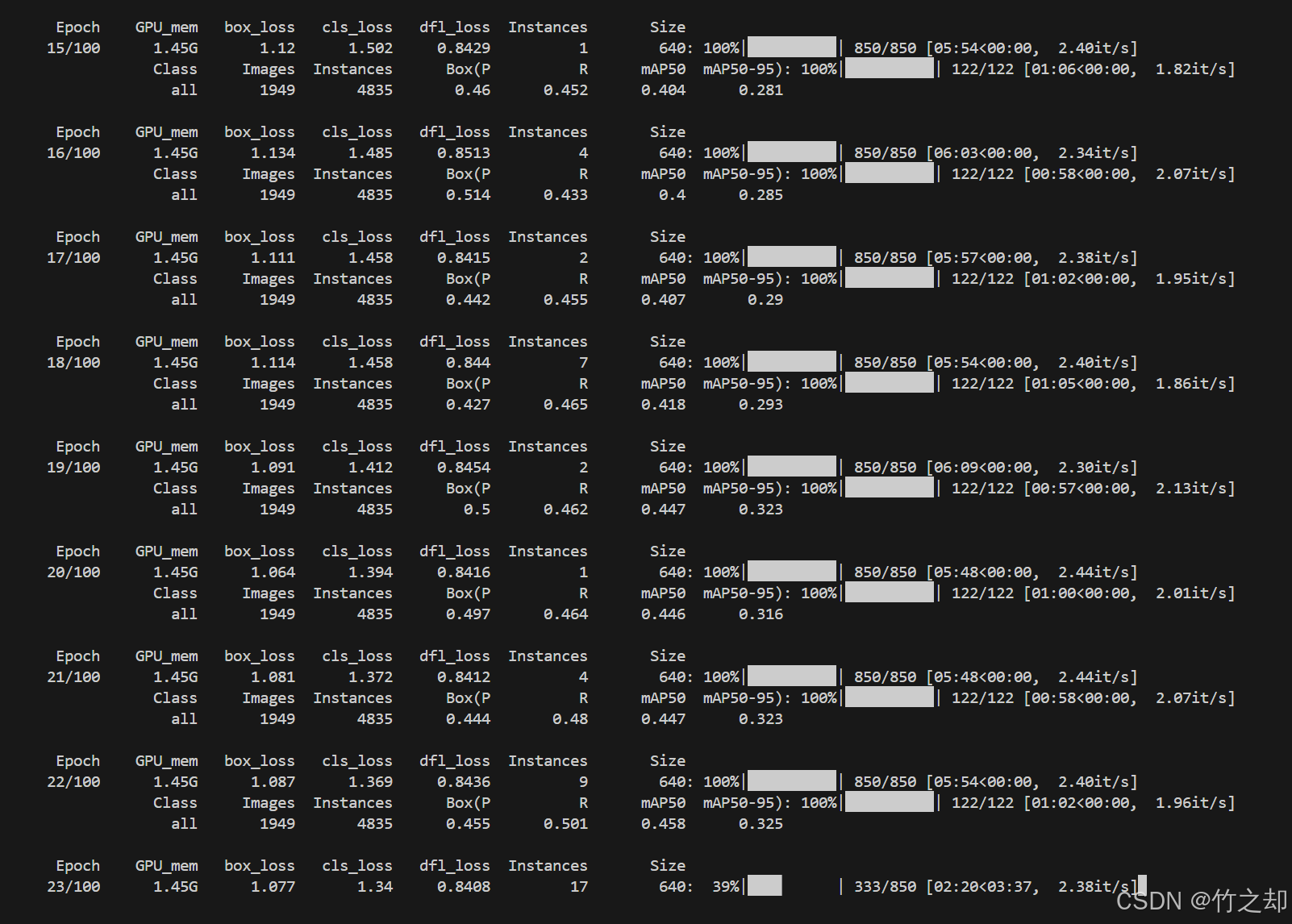
使用Yolov8 训练交通标志数据集:TT100K数据集划分
使用Yolov8 训练交通标志数据集:TT100K数据集划分(一) 一、数据集下载二、划分数据集三、目录放置 一、数据集下载 官方网址:TT100K 数据集对比 源码如下: def classes(filedir):with open(filedir) as f:classes …...

NLP学习路线图(十三):正则表达式
在自然语言处理(NLP)的浩瀚宇宙中,原始文本数据如同未经雕琢的璞玉。而文本预处理,尤其是其中至关重要的正则表达式技术,正是将这块璞玉转化为精美玉器的核心工具集。本文将深入探讨正则表达式在NLP文本预处理中的原理…...

[VMM]现代 CPU 中用于加速多级页表查找的Page‐Table Entry原理
现代 CPU 中用于加速多级页表查找的Page‐Table Entry原理 摘要:以下从背景、结构、查找流程、一致性与性能影响等方面,详细介绍现代 CPU 中用于加速多级页表查找的 Page-Walk Cache(也称 Walker Cache 或 Page‐Table Entry Cache࿰…...

javaweb-maven以及http协议
1.maven坐标: 坐标是资源的唯一标识,通过该坐标可以唯一定位资源位置; 2.坐标的组成: groupId:定义当前项目隶书的组织名称; artifactId:定义当前maven项目名称 version:定义项目版本 3.依…...

华为OD机试真题—— 最少数量线段覆盖/多线段数据压缩(2025A卷:100分)Java/python/JavaScript/C++/C语言/GO六种最佳实现
2025 A卷 100分 题型 本文涵盖详细的问题分析、解题思路、代码实现、代码详解、测试用例以及综合分析; 并提供Java、python、JavaScript、C++、C语言、GO六种语言的最佳实现方式! 2025华为OD真题目录+全流程解析/备考攻略/经验分享 华为OD机试真题《最少数量线段覆盖/多线段数…...

C语言创意编程:用趣味实例玩转基础语法(2)
文章目录 0. 前言1. 📊 动态条形图1.1 程序效果展示1.2 完整代码解析1.3 关键技术详解1.3.1 Unicode字符应用1.3.2 函数封装思想1.3.3 输入处理1.3.4 跨平台考虑 2. 🔤 字母金字塔2.1 程序效果展示2.2 完整代码解析2.3 关键技术详解2.3.1 嵌套循环结构2.…...

关于近期中国移动民用家庭网络,新增的UDP网络限制。
在近期中国移动在全国一定范围普及新的打击 “PCDN、P2P、HY/HY2” 等流氓网络应用的技术方案,并接入在 “省/州” 的边界网关路由上。 根据遥测数据的具体研究分析,且本人曾非常生气的详细质询过,移动城域网管理人员,可以确认该技…...

OpenCV CUDA模块图像处理------颜色空间处理之GPU 上对两张带有 Alpha 通道的图像进行合成操作函数alphaComp()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 该函数用于在 GPU 上对两张带有 Alpha 通道的图像进行合成操作。支持多种常见的 Alpha 合成模式(Porter-Duff 合成规则)&…...

OpenWebUI(1)源码学习构建
1. 前言 通过docker镜像拉取安装就不介绍了,官方的命令很多。本节主要撸一撸源码,所以,本地构建 2. 技术框架和启动环境 后端python,前端svelte 环境要求:python > 3.11 ,Node.js > 20.10 3. 源…...

npm error Cannot find module ‘negotiator‘ 的处理
本想运行npm create vuelatest,但提示: npm error code MODULE_NOT_FOUND npm error Cannot find module negotiator npm error Require stack: npm error - C:\Users\Administrator\AppData\Roaming\nvm\v18.16.1\node_modules\npm\node_modules\tuf-j…...

爬虫入门指南-某专利网站的专利数据查询并存储
免责声明 本教程仅用于教育目的,演示如何合法获取公开专利数据。在实际操作前,请务必: 1. 仔细阅读目标网站的robots.txt文件和服务条款 2. 控制请求频率,避免对服务器造成负担 3. 仅获取和使用公开数据 4. 不用于商业用途或…...

SQL(Database Modifications)
目录 Insertion Specifying Attributes in INSERT Adding Default Values(缺省值) Inserting Many Tuples Creating a Table Using the SELECT INTO Statement Deletion Example: Deletion Semantics of Deletion Updates Example: Update Sev…...
