PINNs案例——二维磁场计算
基于物理信息的神经网络是一种解决偏微分方程计算问题的全新方法…
有关PINN基础详见:PINNs案例——中心热源温度场预测问题的torch代码
今日分享代码案例:二维带电流源磁场计算
该案例参考学习论文:
[1]张宇娇,孙宏达,赵志涛,徐斌,黄雄峰.基于物理信息神经网络的电磁场计算方法[J/OL].电工技术学报.
结果前瞻

问题场景
- ** 求解域** 案例选取边长为 10 的正方形区域作为研究对象,即定义域为
Ω = [ 0 , 10 ] × [ 0 , 10 ] \Omega = [0, 10] \times [0, 10] Ω=[0,10]×[0,10]。以正方形左下角为原点,正方形区域内包含一个带电流密度为1的导体,导体区域为 Ω = [ 4 , 2 ] × [ 6 , 8 ] \Omega = [4, 2] \times [6, 8] Ω=[4,2]×[6,8]。 - **参数设定:**导体处 J = 1 J = 1 J=1,导体材料为铜(copper),其余区域为空气(air),磁导率 γ \gamma γ 均为1
- **边界条件:**方形四周边界的矢量磁位为0(理想导体边界)
- **求解量:**区域内二维稳态磁场分布(矢量)

PINNs理论求解
在本案例中,我们引入矢量磁位 $ \mathbf{A} $ 来辅助磁场的计算。矢量磁位A设定为:
B = ∇ × A \mathbf{B} = \nabla \times \mathbf{A} B=∇×A
其中, B \mathbf{B} B 表示磁场强度,该关系表明磁场是矢量磁位的旋度。
在该正方形区域内,矢量磁位 $ A_z(x, y) $ 满足麦克斯韦方程,引入矢量磁位A后在二维稳态下,其数学表达式为:
( ∂ 2 A z ∂ x 2 + ∂ 2 A z ∂ y 2 ) = − μ J z \left( \frac{\partial^2 A_z}{\partial x^2} + \frac{\partial^2 A_z}{\partial y^2} \right) =-\mu J_z (∂x2∂2Az+∂y2∂2Az)=−μJz
其中:
μ \mu μ 为材料的磁导率,表示材料对磁场的响应能力;
J z J_z Jz 为电流密度在 z z z 方向的分量,表示单位面积内电流的大小;
A z ( x , y ) A_z(x, y) Az(x,y) 为矢量磁位在 z z z 方向的分量,通常用于描述二维平面内的磁场分布。
这种方程形式常见于静电学或静磁学中的泊松方程,用于描述在存在源(如电荷或电流)的情况下,势函数(如矢量磁位)的空间分布。矢量磁位的引入使得磁场的计算更为简便,尤其是在处理对称性问题或边界条件时。
本次案例中,由于存在铜导体区域(有源)和空气域(无源),故采用PINNs案例——多介质分区热传导中相同的分区思想。此处不过多介绍
损失函数可以表示为:
- PDE 残差项: 控制方程如下:
Loss PDE = 1 N c ∑ i = 1 N c ∣ f ( x c i , y c i ) ∣ 2 \text{Loss}_{\text{PDE}} = \frac{1}{N_c} \sum_{i=1}^{N_c} \left| f\left( x_c^i, y_c^i \right) \right|^2 LossPDE=Nc1i=1∑Nc f(xci,yci) 2
f ( x c i , y c i ) = ( ∂ 2 A z ∂ x 2 + ∂ 2 A z ∂ y 2 ) + μ J z f\left( x_c^i, y_c^i \right) = \left( \frac{\partial^2 A_z}{\partial x^2} + \frac{\partial^2 A_z}{\partial y^2} \right) +\mu J_z f(xci,yci)=(∂x2∂2Az+∂y2∂2Az)+μJz
注意: 由于PDE损失中需加入 μ 0 \mu_{0} μ0,而 μ 0 = 4 π ∗ 10 − 7 \mu_{0} = 4\pi * 10^{-7} μ0=4π∗10−7 数量级过小,会对神经网络的训练带来较大困难。故需对PDE方程进行简单的无量纲化操作,令 A ′ = A / μ 0 A' = A/\mu_0 A′=A/μ0, 于是可以得到 f ( x c i , y c i ) = ( ∂ 2 A z ′ ∂ x 2 + ∂ 2 A z ′ ∂ y 2 ) + μ r J z f\left( x_c^i, y_c^i \right) = \left( \frac{\partial^2 A_z'}{\partial x^2} + \frac{\partial^2 A_z'}{\partial y^2} \right) +\mu_r J_z f(xci,yci)=(∂x2∂2Az′+∂y2∂2Az′)+μrJz.预测后再将A乘 μ 0 \mu_0 μ0以还原A
- 边界条件项:在多介质问题中,边界条件除矢量磁位A=0的方形边界条件,还要添加不同介质交界面的连续性边界条件。
-
固定温度边界:
Loss BC = 1 N b ∑ i = 1 N b ∣ A ( x b i , y b i ) ∣ 2 \text{Loss}_{\text{BC}} = \frac{1}{N_b} \sum_{i=1}^{N_b} \left|A\left( x_b^i, y_b^i \right) \right|^2 LossBC=Nb1i=1∑Nb A(xbi,ybi) 2 -
介质交界面:
此案例中以A的第一类和第二类边界条件作为介质交界面的连续性条件
第一类边界条件:
Loss I1 = 1 N I ∑ j = 1 N I ∣ A p ( x I j ) − A p + 1 ( x I j ) ∣ 2 \text{Loss}_{\text{I1}} = \frac{1}{N_{I}}\sum_{j=1}^{N_{I}}\left| A_{p}\left(x_{I}^{j}\right)-A_{p+1}\left(x_{I}^{j}\right)\right|^{2} LossI1=NI1j=1∑NI Ap(xIj)−Ap+1(xIj) 2
第二类边界条件(不同介质在边界面上矢量磁位法向导数与磁导率的乘积连续):
Loss I2 = 1 N I ∑ j = 1 N I ∣ γ p ∂ A p ( x I j ) ∂ n − γ p + 1 ∂ A p + 1 ( x I j ) ∂ n ∣ 2 \text{Loss}_{\text{I2}} = \frac{1}{N_{I}}\sum_{j=1}^{N_{I}}\left|\gamma_{p}\frac{\partial A_{p}\left(x_{I}^{j}\right)}{\partial n}-\gamma_{p+1}\frac{\partial A_{p+1}\left(x_{I}^{j}\right)}{\partial n}\right|^{2} LossI2=NI1j=1∑NI γp∂n∂Ap(xIj)−γp+1∂n∂Ap+1(xIj) 2
其中:
- N I N_I NI 表示介质边界点的点数
- A p A_p Ap 表示第P个介质的矢量磁位
- γ p \gamma_ {p} γp 表示第P个介质的热导率
训练
采用10000次adam优化与lbfgs优化器进行优化。各项损失收敛过程如下,收敛效果良好:

复现结果



comsol仿真结果


可见结果吻合良好
pytorch代码
为避免繁杂的点生成,作者编写了一组点生成函数,使用时单独建立points_generator.py,并在训练代码中引入。
points_generator.py
import numpy as np
from pyDOE import lhsdef generate_boundary_points(x_min, y_min, x_max, y_max, n):# 计算每条边上的点数num_points_x = int((x_max - x_min) * n) + 1num_points_y = int((y_max - y_min) * n) + 1# 生成每条边上的点bottom_edge = np.array([np.linspace(x_min, x_max, num_points_x), np.full(num_points_x, y_min)]).Ttop_edge = np.array([np.linspace(x_min, x_max, num_points_x), np.full(num_points_x, y_max)]).Tleft_edge = np.array([np.full(num_points_y, x_min), np.linspace(y_min, y_max, num_points_y)]).Tright_edge = np.array([np.full(num_points_y, x_max), np.linspace(y_min, y_max, num_points_y)]).T# 合并所有边上的点,去掉重复的角点boundary_points = np.concatenate([bottom_edge, top_edge[1:], left_edge[1:-1], right_edge[1:-1]])boundary_vertical = np.concatenate([left_edge[1:-1], right_edge[1:-1]])boundary_horizontal = np.concatenate([bottom_edge, top_edge[1:]])return boundary_points,boundary_vertical,boundary_horizontaldef generate_internal_points(x_min, y_min, x_max, y_max, n):# 计算内部点的网格x = np.linspace(x_min, x_max, int((x_max - x_min) * n) + 1)y = np.linspace(y_min, y_max, int((y_max - y_min) * n) + 1)x_grid, y_grid = np.meshgrid(x, y)# 去掉边界点x_grid = x_grid[1:-1, 1:-1]y_grid = y_grid[1:-1, 1:-1]# 将网格点转换为一维数组internal_points = np.array([x_grid.flatten(), y_grid.flatten()]).Treturn internal_pointsdef generate_mask(points, x_min, y_min, x_max, y_max):# 检查每个点是否在矩形区域内mask = (points[:, 0] >= x_min) & (points[:, 0] <= x_max) & (points[:, 1] >= y_min) & (points[:, 1] <= y_max)return maskdef lhs_internal_points(x_min, y_min, x_max, y_max, n): '''使用超拉丁立方采样矩形区域内的点'''ub = np.array([x_max, y_max])lb = np.array([x_min, y_min])internal_points = lb + (ub - lb) * lhs(2, n)return internal_points
训练代码
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
from torch.autograd import grad
import time
import datetime
import points_generator as pgdevice = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")# 设置空间尺寸
length = 10.0
width = 10.0#真空磁导率
mu0 = 4*np.pi*1e-7
mu_air = 1
mu_copper = 1# Generate boundary points using NumPy
# boundary_bottom = np.stack([np.linspace(0, length, N_each_boundary), np.zeros(N_each_boundary)], axis=1) # 下边界
# boundary_top = np.stack([np.linspace(0, length, N_each_boundary), np.ones(N_each_boundary) * width], axis=1) # 上边界
# boundary_left = np.stack([np.zeros(N_each_boundary), np.linspace(0, width, N_each_boundary)], axis=1) # 左边界
# boundary_right = np.stack([np.ones(N_each_boundary) * length, np.linspace(0, width, N_each_boundary)], axis=1) # 右边界boundary,_,_ = pg.generate_boundary_points(0,0,width,length,8)# Concatenate boundary points
boundary = torch.tensor(boundary,dtype=torch.float32).to(device)# 生成公共界面上的点
interface_points,interface_vertical,interface_horizontal = pg.generate_boundary_points(4,2,6,8,8)# Convert NumPy arrays to Torch tensors
interface_points = torch.tensor(interface_points,dtype=torch.float32).to(device)
interface_vertical = torch.tensor(interface_vertical,dtype=torch.float32).to(device)
interface_horizontal = torch.tensor(interface_horizontal,dtype=torch.float32).to(device)# 生成板内部的点
air_points = pg.generate_internal_points(0,0,width,length,8)
mask = pg.generate_mask(air_points,4,2,6,8)
air_points = air_points[~mask]
copper_points = pg.generate_internal_points(4,2,6,8,8)# Convert NumPy arrays to Torch tensors
air_points = torch.tensor(air_points,dtype=torch.float32).to(device)
copper_points = torch.tensor(copper_points,dtype=torch.float32).to(device)# Concatenate all points
internal_points = torch.cat([copper_points,air_points],dim=0)
all_points = torch.cat([boundary, interface_points, copper_points,air_points], dim=0)def pointsplot():plt.figure(figsize=(8, 8))plt.scatter(air_points[:, 0].numpy(), air_points[:, 1].numpy(), s=10, c='blue', alpha=0.5,label='air_points')plt.scatter(copper_points[:, 0].numpy(), copper_points[:, 1].numpy(), s=10, c='red', alpha=0.5,label='copper_points')plt.scatter(boundary[:, 0].numpy(), boundary[:, 1].numpy(), s=10, c='black', alpha=0.5,label='boundary')plt.scatter(interface_points[:, 0].numpy(), interface_points[:, 1].numpy(), s=10, c='orange', alpha=0.5,label='interface_points')plt.xlabel('X ')plt.ylabel('Y')plt.title('points visualize')plt.legend()plt.grid(True)plt.show()# 打印各部分点数和总点数
print(f"边界点数: {boundary.shape[0]}")
print(f"界面点数: {interface_points.shape[0]}")
print(f"内部点数: {internal_points.shape[0]}")
print(f"总点数: {all_points.shape[0]}")
pointsplot()class layer(nn.Module):def __init__(self, n_in, n_out, activation):super().__init__()self.layer = nn.Linear(n_in, n_out)self.activation = activationdef forward(self, x):x = self.layer(x)if self.activation:x = self.activation(x)return xdef weights_init(m):if isinstance(m, nn.Linear):torch.nn.init.xavier_uniform_(m.weight.data)torch.nn.init.zeros_(m.bias.data)
class DNN(nn.Module):# dim_in 和 dim_out:分别为网络的输入和输出维度,n_layer 和 n_node:n_layer 表示隐藏层的数量, activation为激活函数,ub 和 lb:分别是区域的上界和下界,用于输入的归一化处理。def __init__(self, dim_in, dim_out, n_layer, n_node, activation = nn.Tanh()):super().__init__()self.net = nn.ModuleList()self.net.append(layer(dim_in, n_node, activation)) #第一个输入层for _ in range(n_layer):self.net.append(layer(n_node, n_node, activation))self.net.append(layer(n_node, dim_out, activation=None)) #最后一个输出层self.net.apply(weights_init) # weights_init 函数对网络的权重和偏置进行初始化(例如 Xavier 初始化),从而提供较好的初始收敛性。def forward(self, x):out = xfor layer in self.net:out = layer(out)return outclass PINN:def __init__(self) -> None:# 定义每个介质的网络self.nets = [DNN(dim_in=2, dim_out=1, n_layer=6, n_node=80).to(device),DNN(dim_in=2, dim_out=1, n_layer=6, n_node=80).to(device),# DNN(dim_in=2, dim_out=1, n_layer=6, n_node=50).to(device)]self.lbfgs = torch.optim.LBFGS(params=[p for net in self.nets for p in net.parameters()],lr=0.1,max_iter=20000,max_eval=20000,tolerance_grad=1e-5,tolerance_change= 1 * np.finfo(float).eps,history_size=50,line_search_fn="strong_wolfe",)#分别定义了 LBFGS 和 Adam 两种优化器。LBFGS 是一种基于二阶信息的优化算法,适用于物理信息神经网络的优化;Adam 是一种常用的一阶优化方法,用于更新网络权重。# self.adam = [# torch.optim.Adam(net.parameters(), lr=1e-4) for net in self.nets# ]self.adam = torch.optim.Adam(params=[p for net in self.nets for p in net.parameters()], lr=1e-5)self.losses = {"bc": [], "pde": [], "interface": [], "loss": []}self.iter = 0def predict(self, xy):output = torch.zeros(xy.shape[0], 1) # Ensure output has the right shapemask = pg.generate_mask(xy,4,2,6,8)output[mask] = self.nets[0](xy[mask])output[~mask] = self.nets[1](xy[~mask])return outputdef bc_loss(self):boundary.requires_grad = TrueA = self.predict(boundary)# 边界条件处理mse_bc = torch.mean(A**2)#边界损失l_bc = mse_bcreturn l_bcdef interface_bc_loss(self):"""计算公共边界条件损失函数"""interface_vertical.requires_grad = Trueinterface_horizontal.requires_grad = TrueA_interface_1_vertical = self.nets[0](interface_vertical)A_interface_2_vertical = self.nets[1](interface_vertical)A_interface_1_horizontal = self.nets[0](interface_horizontal)A_interface_2_horizontal = self.nets[1](interface_horizontal)# 第一边界条件l_1 = torch.mean(torch.square(A_interface_1_vertical - A_interface_2_vertical)) + torch.mean(torch.square(A_interface_1_horizontal - A_interface_2_horizontal))# 第二边界条件grad_1_vertical = grad(A_interface_1_vertical.sum(), interface_vertical, create_graph=True)[0][:, 0:1]grad_2_vertical = grad(A_interface_2_vertical.sum(), interface_vertical, create_graph=True)[0][:, 0:1]grad_1_horizontal = grad(A_interface_1_horizontal.sum(), interface_horizontal, create_graph=True)[0][:, 1:2]grad_2_horizontal = grad(A_interface_2_horizontal.sum(), interface_horizontal, create_graph=True)[0][:, 1:2]grad_1 = torch.cat([grad_1_vertical, grad_1_horizontal])grad_2 = torch.cat([grad_2_vertical, grad_2_horizontal])l_2 = torch.mean(torch.square(mu_copper*grad_1-mu_air*grad_2))return l_1+l_2def pde_loss(self, xy):xy = xy.clone().detach().requires_grad_(True)mask = pg.generate_mask(xy, 4, 2, 6, 8)# 铜导体区域xy_copper = xy[mask]A_copper = self.nets[0](xy_copper)grad_A_copper = grad(A_copper.sum(), xy_copper, create_graph=True)[0]dA_dx_copper = grad_A_copper[:, 0:1]dA_dy_copper = grad_A_copper[:, 1:2]d2A_dx2_copper = grad(dA_dx_copper.sum(), xy_copper, create_graph=True)[0][:, 0:1]d2A_dy2_copper = grad(dA_dy_copper.sum(), xy_copper, create_graph=True)[0][:, 1:2]nu_copper = 1 / (mu_copper)pde_copper = d2A_dx2_copper + d2A_dy2_copper + 1loss_copper = torch.mean((nu_copper * pde_copper) ** 2)# 空气区域xy_air = xy[~mask]A_air = self.nets[1](xy_air)grad_A_air = grad(A_air.sum(), xy_air, create_graph=True)[0]dA_dx_air = grad_A_air[:, 0:1]dA_dy_air = grad_A_air[:, 1:2]d2A_dx2_air = grad(dA_dx_air.sum(), xy_air, create_graph=True)[0][:, 0:1]d2A_dy2_air = grad(dA_dy_air.sum(), xy_air, create_graph=True)[0][:, 1:2]nu_air = 1 / (mu_air)pde_air = d2A_dx2_air + d2A_dy2_airloss_air = torch.mean((nu_air * pde_air) ** 2)return loss_copper + loss_airdef closure(self):self.lbfgs.zero_grad()self.adam.zero_grad()mse_bc = self.bc_loss()mse_pde = self.pde_loss(internal_points)mse_interface = self.interface_bc_loss()loss = mse_pde +mse_bc+mse_interfaceloss.backward()self.losses["bc"].append(mse_bc.detach().cpu().item())self.losses["pde"].append(mse_pde.detach().cpu().item())self.losses["interface"].append(mse_interface.detach().cpu().item())self.losses["loss"].append(loss.cpu().item())self.iter += 1print(f"\r It: {self.iter} Loss: {loss.item():.5e} BC: {mse_bc.item():.3e} PDE: {mse_pde.item():.3e} Interface: {mse_interface.item():.3e}",end="",)if self.iter % 100 == 0:print("")return lossdef save_model(self, path):"""保存模型和训练状态:param path: 保存文件路径"""save_dict = {"nets": [net.state_dict() for net in self.nets], # 保存所有子网络的参数"optimizers": [self.adam.state_dict(), self.lbfgs.state_dict()], # 保存优化器状态"losses": self.losses, # 保存损失记录"iteration": self.iter, # 保存当前迭代次数}torch.save(save_dict, path)print(f"模型已保存到 {path}")def load_model(self, path):"""加载模型和训练状态:param path: 加载文件路径"""checkpoint = torch.load(path, map_location=device)# 加载每个网络的参数for net, state_dict in zip(self.nets, checkpoint["nets"]):net.load_state_dict(state_dict)# 加载每个优化器的状态for opt, state_dict in zip([self.adam, self.lbfgs], checkpoint["optimizers"]):opt.load_state_dict(state_dict)# 加载其他训练状态self.losses = checkpoint["losses"]self.iter = checkpoint["iteration"]print(f"模型已从 {path} 加载")def plotLoss(losses_dict, path, info=["BC", "PDE","Interface","Loss"]):fig, axes = plt.subplots(1, 4, sharex=True, sharey=True, figsize=(12, 6))axes[0].set_yscale("log")for i, j in zip(range(4), info):axes[i].plot(losses_dict[j.lower()])axes[i].set_title(j)plt.show()fig.savefig(path)if __name__ == "__main__":pinn = PINN()start_time = time.time()for i in range(10000):pinn.closure()pinn.adam.step()pinn.lbfgs.step(pinn.closure)print("--- %s seconds ---" % (time.time() - start_time))print(f'-- {(time.time() - start_time)/60} mins --')now = datetime.datetime.now()# 格式化时间为字符串,例如:2024-11-28_15-30-00time_str = now.strftime("%m%d-%H%M")pinn.save_model( f"Param{time_str}.pt")plotLoss(pinn.losses, f"LossCurve{time_str}.png", )
预测代码
import numpy as np
import matplotlib.pyplot as plt
import torch
from main import PINN, mu0
from scipy.interpolate import griddatadevice = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")pinn = PINN()
# 定义网格的分辨率
grid_size_x = 200
grid_size_y = 200
x_min = 0
x_max = 10
y_min =0
y_max = 10# 生成x和y坐标的等距网格点
x = np.linspace(x_min, x_max, grid_size_x)
y = np.linspace(y_min, y_max, grid_size_y)
X, Y = np.meshgrid(x, y)# 将网格点转化为输入格式(grid_size * grid_size, 2)
xy_grid = np.hstack((X.reshape(-1, 1), Y.reshape(-1, 1)))
xy_grid = torch.tensor(xy_grid, dtype=torch.float32).to(device)
time_str = '0531-1718'
pinn.load_model(f"Param{time_str}.pt")# 预测温度
with torch.no_grad():A_pred = pinn.predict(xy_grid)*mu0# 将预测的温度值转化为numpy格式,并恢复为网格形状
A_pred = A_pred.detach().cpu().numpy().reshape(Y.shape)plt.figure(figsize=(8, 6))
plt.contourf(x,y,A_pred,levels=50, cmap='jet')
plt.colorbar(label='A')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Predicted A Distribution')
plt.savefig(f"Sol{time_str}.jpg")
plt.show()# 计算磁场分量 Bx 和 By
Ay, Ax = np.gradient(A_pred, y, x)
Bx = Ay
By = -Ax
B = np.sqrt(Bx**2+By**2)skip = 10 # 每隔 skip 个点绘制一个箭头# 绘制磁场矢量图
plt.figure(figsize=(8, 6))
# 使用 B_magnitude 作为颜色的依据
quiver = plt.quiver(X[::skip, ::skip], Y[::skip, ::skip], Bx[::skip, ::skip], By[::skip, ::skip],B[::skip, ::skip], cmap='rainbow')
#设置图的背景色
# plt.gca().set_facecolor('black')
plt.colorbar(quiver, label='Magnetic Field Magnitude')
plt.title('Magnetic Field Vector Plot')
plt.xlabel('x')
plt.ylabel('y')
plt.grid()
plt.show()
如果代码运行有问题或对内容有疑问,都可以后台私信哦!
期待下一期PINNs案例代码分享吧!
基于物理信息的神经网络是一种解决偏微分方程计算问题的全新方法…
有关PINN基础详见:PINNs案例——中心热源温度场预测问题的torch代码
今日分享代码案例:二维带电流源磁场计算
该案例参考学习论文:
[1]张宇娇,孙宏达,赵志涛,徐斌,黄雄峰.基于物理信息神经网络的电磁场计算方法[J/OL].电工技术学报.
结果前瞻

问题场景
- **求解域:**案例选取边长为 10 的正方形区域作为研究对象,即定义域为
$ \Omega = [0, 10] \times [0, 10] 。以正方形左下角为原点,正方形区域内包含一个带电流密度为 1 的导体,导体区域为 。以正方形左下角为原点,正方形区域内包含一个带电流密度为1的导体,导体区域为 。以正方形左下角为原点,正方形区域内包含一个带电流密度为1的导体,导体区域为 \Omega = [4, 2] \times [6, 8] $。 - **参数设定:**导体处 J = 1 J = 1 J=1,导体材料为铜(copper),其余区域为空气(air),磁导率 γ \gamma γ 均为1
- **边界条件:**方形四周边界的矢量磁位为0(理想导体边界)
- **求解量:**区域内二维稳态磁场分布(矢量)

PINNs理论求解
在本案例中,我们引入矢量磁位 $ \mathbf{A} $ 来辅助磁场的计算。矢量磁位A设定为:
B = ∇ × A \mathbf{B} = \nabla \times \mathbf{A} B=∇×A
其中, B \mathbf{B} B 表示磁场强度,该关系表明磁场是矢量磁位的旋度。
在该正方形区域内,矢量磁位 $ A_z(x, y) $ 满足麦克斯韦方程,引入矢量磁位A后在二维稳态下,其数学表达式为:
( ∂ 2 A z ∂ x 2 + ∂ 2 A z ∂ y 2 ) = − μ J z \left( \frac{\partial^2 A_z}{\partial x^2} + \frac{\partial^2 A_z}{\partial y^2} \right) =-\mu J_z (∂x2∂2Az+∂y2∂2Az)=−μJz
其中:
- $ \mu $ 为材料的磁导率,表示材料对磁场的响应能力;
- $ J_z $ 为电流密度在 $ z $ 方向的分量,表示单位面积内电流的大小;
- $ A_z(x, y) $ 为矢量磁位在 $ z $ 方向的分量,通常用于描述二维平面内的磁场分布。
这种方程形式常见于静电学或静磁学中的泊松方程,用于描述在存在源(如电荷或电流)的情况下,势函数(如矢量磁位)的空间分布。矢量磁位的引入使得磁场的计算更为简便,尤其是在处理对称性问题或边界条件时。
本次案例中,由于存在铜导体区域(有源)和空气域(无源),故采用PINNs案例——多介质分区热传导中相同的分区思想。此处不过多介绍
损失函数可以表示为:
- **PDE 残差项:**控制方程如下:
Loss PDE = 1 N c ∑ i = 1 N c ∣ f ( x c i , y c i ) ∣ 2 \text{Loss}_{\text{PDE}} = \frac{1}{N_c} \sum_{i=1}^{N_c} \left| f\left( x_c^i, y_c^i \right) \right|^2 LossPDE=Nc1i=1∑Nc f(xci,yci) 2
f ( x c i , y c i ) = ( ∂ 2 A z ∂ x 2 + ∂ 2 A z ∂ y 2 ) + μ J z f\left( x_c^i, y_c^i \right) = \left( \frac{\partial^2 A_z}{\partial x^2} + \frac{\partial^2 A_z}{\partial y^2} \right) +\mu J_z f(xci,yci)=(∂x2∂2Az+∂y2∂2Az)+μJz
注意: 由于PDE损失中需加入 μ 0 \mu_{0} μ0,而 μ 0 = 4 π ∗ 10 − 7 \mu_{0} = 4\pi * 10^{-7} μ0=4π∗10−7 数量级过小,会对神经网络的训练带来较大困难。故需对PDE方程进行简单的无量纲化操作,令 A ′ = A / μ 0 A' = A/\mu_0 A′=A/μ0, 于是可以得到 f ( x c i , y c i ) = ( ∂ 2 A z ′ ∂ x 2 + ∂ 2 A z ′ ∂ y 2 ) + μ r J z f\left( x_c^i, y_c^i \right) = \left( \frac{\partial^2 A_z'}{\partial x^2} + \frac{\partial^2 A_z'}{\partial y^2} \right) +\mu_r J_z f(xci,yci)=(∂x2∂2Az′+∂y2∂2Az′)+μrJz.预测后再将A乘 μ 0 \mu_0 μ0以还原A
- 边界条件项:在多介质问题中,边界条件除矢量磁位A=0的方形边界条件,还要添加不同介质交界面的连续性边界条件。
-
固定温度边界:
Loss BC = 1 N b ∑ i = 1 N b ∣ A ( x b i , y b i ) ∣ 2 \text{Loss}_{\text{BC}} = \frac{1}{N_b} \sum_{i=1}^{N_b} \left|A\left( x_b^i, y_b^i \right) \right|^2 LossBC=Nb1i=1∑Nb A(xbi,ybi) 2 -
介质交界面:
此案例中以A的第一类和第二类边界条件作为介质交界面的连续性条件
第一类边界条件:
Loss I1 = 1 N I ∑ j = 1 N I ∣ A p ( x I j ) − A p + 1 ( x I j ) ∣ 2 \text{Loss}_{\text{I1}} = \frac{1}{N_{I}}\sum_{j=1}^{N_{I}}\left| A_{p}\left(x_{I}^{j}\right)-A_{p+1}\left(x_{I}^{j}\right)\right|^{2} LossI1=NI1j=1∑NI Ap(xIj)−Ap+1(xIj) 2
第二类边界条件(不同介质在边界面上矢量磁位法向导数与磁导率的乘积连续):
Loss I2 = 1 N I ∑ j = 1 N I ∣ γ p ∂ A p ( x I j ) ∂ n − γ p + 1 ∂ A p + 1 ( x I j ) ∂ n ∣ 2 \text{Loss}_{\text{I2}} = \frac{1}{N_{I}}\sum_{j=1}^{N_{I}}\left|\gamma_{p}\frac{\partial A_{p}\left(x_{I}^{j}\right)}{\partial n}-\gamma_{p+1}\frac{\partial A_{p+1}\left(x_{I}^{j}\right)}{\partial n}\right|^{2} LossI2=NI1j=1∑NI γp∂n∂Ap(xIj)−γp+1∂n∂Ap+1(xIj) 2
其中:
- $ N_I $ 表示介质边界点的点数
- $ A_p $ 表示第P个介质的矢量磁位
- $ \gamma_ {p} $ 表示第P个介质的热导率
训练
采用10000次adam优化与lbfgs优化器进行优化。各项损失收敛过程如下,收敛效果良好:

复现结果



comsol仿真结果


可见结果吻合良好
pytorch代码
为避免繁杂的点生成,作者编写了一组点生成函数,使用时单独建立points_generator.py,并在训练代码中引入。
points_generator.py
import numpy as np
from pyDOE import lhsdef generate_boundary_points(x_min, y_min, x_max, y_max, n):# 计算每条边上的点数num_points_x = int((x_max - x_min) * n) + 1num_points_y = int((y_max - y_min) * n) + 1# 生成每条边上的点bottom_edge = np.array([np.linspace(x_min, x_max, num_points_x), np.full(num_points_x, y_min)]).Ttop_edge = np.array([np.linspace(x_min, x_max, num_points_x), np.full(num_points_x, y_max)]).Tleft_edge = np.array([np.full(num_points_y, x_min), np.linspace(y_min, y_max, num_points_y)]).Tright_edge = np.array([np.full(num_points_y, x_max), np.linspace(y_min, y_max, num_points_y)]).T# 合并所有边上的点,去掉重复的角点boundary_points = np.concatenate([bottom_edge, top_edge[1:], left_edge[1:-1], right_edge[1:-1]])boundary_vertical = np.concatenate([left_edge[1:-1], right_edge[1:-1]])boundary_horizontal = np.concatenate([bottom_edge, top_edge[1:]])return boundary_points,boundary_vertical,boundary_horizontaldef generate_internal_points(x_min, y_min, x_max, y_max, n):# 计算内部点的网格x = np.linspace(x_min, x_max, int((x_max - x_min) * n) + 1)y = np.linspace(y_min, y_max, int((y_max - y_min) * n) + 1)x_grid, y_grid = np.meshgrid(x, y)# 去掉边界点x_grid = x_grid[1:-1, 1:-1]y_grid = y_grid[1:-1, 1:-1]# 将网格点转换为一维数组internal_points = np.array([x_grid.flatten(), y_grid.flatten()]).Treturn internal_pointsdef generate_mask(points, x_min, y_min, x_max, y_max):# 检查每个点是否在矩形区域内mask = (points[:, 0] >= x_min) & (points[:, 0] <= x_max) & (points[:, 1] >= y_min) & (points[:, 1] <= y_max)return maskdef lhs_internal_points(x_min, y_min, x_max, y_max, n): '''使用超拉丁立方采样矩形区域内的点'''ub = np.array([x_max, y_max])lb = np.array([x_min, y_min])internal_points = lb + (ub - lb) * lhs(2, n)return internal_points
训练代码与预测代码请关注:
相关文章:

PINNs案例——二维磁场计算
基于物理信息的神经网络是一种解决偏微分方程计算问题的全新方法… 有关PINN基础详见:PINNs案例——中心热源温度场预测问题的torch代码 今日分享代码案例:二维带电流源磁场计算 该案例参考学习论文:[1]张宇娇,孙宏达࿰…...

Hive SQL 中 BY 系列关键字全解析:从排序、分发到分组的核心用法
一、排序与分发相关 BY 关键字 1. ORDER BY:全局统一排序 作用:对查询结果进行全局排序,确保最终结果集完全有序(仅允许单个 Reducer 处理数据)。 语法: SELECT * FROM table_name ORDER BY column1 [A…...

数据类型检测有哪些方式?
typeof 其中数组 对象 null都会判断为Object,其他正确 typeof 2 // number typeof true //bolean typeof str //string typeof [] //Object typeof function (){} // function typeof {} //object typeof undefined //undefined typeof null // nullinstanceof 判断…...
算法打开13天
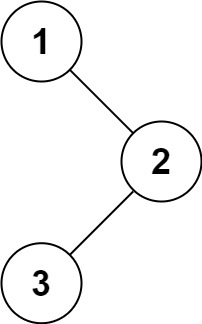
41.前 K 个高频元素 (力扣347题) 给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。 示例 1: 输入: nums [1,1,1,2,2,3], k 2 输出: [1,2]示例 2: 输入: nums [1], k 1 输出: …...

Freeqwq 世界首个免费无限制 分布式 AI 算力平台 https://qwq.aigpu.cn/
官网:Free QWQ - 免费分布式 AI 算力平台 基于来自全国各地 50 台家用电脑的 3090、4080、4090 显卡分布式算力,我们为开发者提供完全免费、无限制的 QwQ 32B 大语言模型 API。无需注册,无需充值,立即获取 API Key 开始使用。 …...

广告拦截器:全方位拦截,畅享无广告体验
在数字时代,广告无处不在。无论是浏览网页、使用社交媒体,还是观看视频,广告的频繁弹出常常打断我们的体验,让人不胜其烦。更令人担忧的是,一些广告可能包含恶意软件,威胁我们的设备安全和个人隐私。AdGuar…...

.net Avalonia应用程序生命周期
.NET Avalonia 应用程序生命周期全解析 在 .NET 开发领域,Avalonia 作为一个跨平台的 UI 框架,为开发者提供了强大的功能和灵活性。了解 Avalonia 应用程序的生命周期,对于构建高效、稳定的应用至关重要。本文将深入探讨 Avalonia 应用程序生…...

主数据编码体系全景解析:从基础到高级的编码策略全指南
在数字化转型的浪潮中,主数据管理(MDM)已成为企业数字化转型的基石。而主数据编码作为MDM的核心环节,其设计质量直接关系到数据管理的效率、系统的可扩展性以及业务决策的准确性。本文将系统性地探讨主数据编码的七大核心策略&…...

Selenium操作指南(全)
🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 大家好,今天带大家一起系统的学习下模拟浏览器运行库Selenium,它是一个用于Web自动化测试及爬虫应用的重要工具。 Selenium测试直接运行在…...

Go语言中的数据类型转换
Go 语言中只有强制类型转换,没有隐式类型转换。 1. 数值类型之间的相互转换 1.1. 整型和整型之间的转换 package main import "fmt"func main() {var a int8 20var b int16 40fmt.Println(int16(a) b)// 60 }1.2. 浮点型和浮点型之间的转换 packag…...

35、请求处理-【源码分析】-自定义参数绑定原理
35、请求处理-【源码分析】-自定义参数绑定原理 自定义参数绑定原理主要涉及Spring Boot如何将HTTP请求中的参数自动绑定到控制器方法的自定义对象参数上。以下是详细的解析: ### 1. 参数解析器的选择 - **HandlerMethodArgumentResolverComposite**: - …...

智绅科技——科技赋能健康养老,构建智慧晚年新生态
当老龄化浪潮与数字技术深度碰撞,智绅科技以 “科技赋能健康,智慧守护晚年” 为核心理念,锚定数字健康与养老服务赛道,通过人工智能、物联网、大数据等技术集成,为亚健康群体与中老年人群构建 “监测 - 预防 - 辅助 - …...

STM32通过KEIL pack包轻松移植LVGL,并学会使用GUI guider
先展示最终实现的功能效果如下: 1.目的与意义 之前在学习STM32移植LVGL图形库的时候,搜到的很多教程都是在官网下载LVGL的文件包,然后一个个文件包含进去,还要添加路径,还要给文件改名字,最后才能修改程序…...

day43 python Grad-CAM
目录 一、为什么需要 Grad-CAM? 二、Grad-CAM 的原理 三、Grad-CAM 的实现 1. 模块钩子(Module Hooks) 2. Grad-CAM 的实现代码 四、学习总结 在深度学习领域,神经网络模型常常被视为“黑盒”,因为其复杂的内部结…...

在 Ubuntu 上挂载其他硬盘的步骤
一、查看当前磁盘信息 打开终端,执行: lsblk 这个命令会列出所有的块设备(包括硬盘和分区)。比如输出可能如下: NAME MAJ:MIN RM SIZE RO TYPE MOUNTPOINT sda 8:0 0 1.8T 0 disk └─sda1 8:1 0 …...

SQL的查询优化
1. 查询优化器 1.1. SQL语句执行需要经历的环节 解析阶段:语法分析和语义检查,确保语句正确;优化阶段:通过优化器生成查询计划;执行阶段:由执行器根据查询计划实际执行操作。 1.2. 查询优化器 查询优化器…...

MCU如何从向量表到中断服务
目录 1、中断向量表 2、编写中断服务例程 中断处理的核心是中断向量表(IVT),它是一个存储中断服务例程(ISR)地址的内存结构。当中断发生时,MCU通过IVT找到对应的ISR地址并跳转执行。本文将深入探讨MCU&am…...

物联网基础概念
入行物联网两年半,想写点东西记录踩过的坑,能让自己反省的同时,也希望能帮到其他小伙伴。 本人仍是小白,请看客朋友谨慎参考。另,本人主要从事智慧用电和智慧医疗行业,其他行业不一定有参考性。 以下所有内…...

Linux线程同步实战:多线程程序的同步与调度
个人主页:chian-ocean 文章专栏-Linux Linux线程同步实战:多线程程序的同步与调度 个人主页:chian-ocean文章专栏-Linux 前言:为什么要实现线程同步线程饥饿(Thread Starvation)示例:抢票问题 …...

【MySQL】事务及隔离性
目录 一、什么是事务 (一)概念 (二)事务的四大属性 (三)事务的作用 (四)事务的提交方式 二、事务的启动、回滚与提交 (一)事务的启动、回滚与提交 &am…...

Leetcode 3566. Partition Array into Two Equal Product Subsets
Leetcode 3566. Partition Array into Two Equal Product Subsets 1. 解题思路2. 代码实现 题目链接:3566. Partition Array into Two Equal Product Subsets 1. 解题思路 这一题我的实现还是比较暴力的,首先显而易见的,若要满足题目要求&…...

yolo目标检测助手:具有模型预测、图像标注功能
在人工智能浪潮席卷各行各业的今天,计算机视觉模型(如 YOLO)已成为目标检测领域的标杆。然而,模型的强大能力需要直观的界面和便捷的工具才能充分发挥其演示、验证与迭代优化的价值。为此,我开发了一款基于 WPF 的桌面…...

传统数据表设计与Prompt驱动设计的范式对比:以NBA投篮数据表为例
引言:数据表设计方法的演进 在数据库设计领域,传统的数据表设计方法与新兴的Prompt驱动设计方法代表了两种截然不同的思维方式。本文将以NBA赛季投篮数据表(shots)的设计为例,深入探讨这两种方法的差异、优劣及适用场景。随着AI技术在数据领…...

2022 RoboCom 世界机器人开发者大赛(睿抗 caip) -高职组(国赛)解题报告 | 科学家
前言 题解 2022 RoboCom 世界机器人开发者大赛(睿抗 caip) -高职组(国赛)。 最后一题还考验能力,需要找到合适的剪枝。 RC-v1 智能管家 分值: 20分 签到题,map的简单实用 #include <bits/stdc.h>using namespace std;int…...

WIN11 Docker Desktop 安装问题解决
windows version 打开windows 命令行,执行 ver显示 Microsoft Windows [版本 10.0.26100.4061]安装docker desktop 后,启动出问题,可以按下面步骤解决 安装 virtual machine plateform 开始 —》 控制面板 ----》程序 ----》启动或关闭w…...

网站服务器出现异常的原因是什么?
网站时企业和个人用户进行提供信息和服务的重要平台,随着时间的推移,网站服务器出现异常情况也是常见的问题之一,这可能会导致网站无法正常访问或者是运行缓慢,会严重影响到用户的体验感,本文就来介绍一下网站服务器出…...

Python实例题:Python3实现图片转彩色字符
目录 Python实例题 题目 代码实现 实现原理 图像预处理: 灰度值计算: 字符映射: 彩色输出: 关键代码解析 1. 字符映射和灰度计算 2. 图像模式输出 3. 命令行参数处理 使用说明 基本用法(终端输出&#x…...

同一机器下通过HTTP域名访问其他服务器进程返回504问题记录
我这边项目的服务器有好几个类型节点,每个节点为一个进程,不同节点间通过HTTP来通讯,当前这几个类型的节点都部署在同一台机器上,然后我再测试某个节点到另一个节点的http通讯时,发现一个奇怪的现象: 1. 我…...

基于物联网(IoT)的电动汽车(EVs)智能诊断
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从&#x…...

JDBC+HTML+AJAX实现登陆和单表的CRUD
JDBCHTMLAJAX实现登陆和单表的CRUD 导入maven依赖 <?xml version"1.0" encoding"UTF-8"?><project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance" xsi:schemaLocatio…...
