【CF】Day72——Codeforces Round 890 (Div. 2) CDE1 (二分答案 | 交互 + 分治 | ⭐树上背包)
C. To Become Max
题目:

思路:
二分挺好想的,但是check有点不好写
看到最大值,试试二分,如果 x 可以,那么 x - 1 肯定也可以,所以具有单调性,考虑二分
如何check呢?由于 n 很小,我们可以考虑 n² 的 check,我们可以考虑枚举每一个位置为 mid,那么如果这个位置要是 mid 那么下一个位置就起码是 mid - 1,以此类推,直接模拟即可
特别的,由于 n 处无法继续往后,所以记得判断一下
代码:
#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "Yes\n"
#define no cout << "No\n"void solve()
{int n, K;cin >> n >> K;vector<int> A(n);int mx = 0;for (int i = 0; i < n; i++){cin >> A[i];mx = max(A[i], mx);}auto check = [&](int mid) ->bool{for (int i = 0; i < n - 1; i++){int nd = 0;int m = mid;int j = i;for (; j < n; j++){if (A[j] >= m){break;}nd += m - A[j];m--;}if (K >= nd && A[j] >= m && j < n){return true;}}return false;};int l = mx, r = 1e18;while (l + 1 < r){int mid = l + r >> 1;if (check(mid)){l = mid;}else{r = mid;}}if (check(r)){cout << r << endl;return;}cout << l << endl;
}signed main()
{cin.tie(0)->sync_with_stdio(false);int t = 1;cin >> t;while (t--){solve();}return 0;
}D. More Wrong
题目:

 思路:
思路:
找结论题
交互题通常喜欢二分,这里也不例外
我们先要知道一个关键点,假设 x 是最大值的位置,那么对于任意一个左端点 l,都有以下结论: [l, x-1] = [l, x],即这两个区间的逆序对一定相同,因为 x 是最大值,那么加在后面是无影响的
如果我们直接一个一个枚举的话肯定会超时,所以我们考虑优化,我们考虑分治,我们像线段树一样每次取一半,然后把每个子区间的最大值求出来,再依次合并
具体的,假设我们要求 [l r] 的最大值,我们要先求出 [l mid] [mid+1 r] 的两个最大值的位置 Lmx和 Rmx,其中 mid = (l+r) / 2,然后根据我们的结论,如果 Rmx 是最大值,那么就有 [Lmx Rmx - 1] = [Lmx Rmx],否则就是 Lmx 是区间的最大值
模拟即可
代码:
#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "Yes\n"
#define no cout << "No\n"int ask(int l,int r)
{if (l == r)return 0;else{cout << "? " << l << " " << r << endl;int w = 0;cin >> w;return w;}
}int solve(int l,int r)
{if (l == r){return r;}else{int mid = l + r >> 1;int Lmx = solve(l, mid), Rmx = solve(mid + 1, r);if (ask(Lmx,Rmx) == ask(Lmx,Rmx-1)){return Rmx;}return Lmx;}
}signed main()
{int t = 1;cin >> t;while (t--){int n; cin >> n;int w = solve(1, n);cout << "! " << w << endl;}return 0;
}E1. PermuTree (easy version)
题目:
 思路:
思路:
看似lca?实则dp
这一题我们看着好像无法下手,但是注意到 n <= 5000,我们可以考虑 n² 做法
题目意思转化一下就是你可以自由分配树的顶点的权值 val[i],使得所有权值最后是一个排列,最后的答案是对于任意一个父节点选取其两个子节点 (u,v),满足 val[u] < val[fa] < val[v] 的(u,v)对数
我们可以将 lca,变化一下,因为我们其实不需要知道子节点具体是什么,我们只在乎它的权值,那么我们就可以考虑枚举每一个节点当这个 lca
那么如果这个点是 lca,那我们如何计算其奉献呢?我们贪心的想,我们肯定是考虑将其子树分成两个子集,一个是权值全小于父节点,一个是权值全大于父节点,那么答案就是 size_small * size_big
那么问题再转化一下,对于每一个子树,我们可以考虑其是大于还是小于父节点,然后对于所有情况求最大值,那么这其实就是一个树上01背包,对于每个子树我们都可以选or不选,所以直接套就行了
那为什么我们一定可以这样构造呢?我们这样想,我们肯定是先分配最小的子树,比如对于下面例子
我们可以分配给子树小的,然后再给父节点一个中间值,然后再分配比父节点大的子树,如 1 2 | 3 | 4 5 | 6 7 这样,不过由于不需要我们输出具体的权值,所以我们不需要考虑具体的构造,但是肯定是能构造的
代码:
#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define int long long
#define yes cout << "Yes\n"
#define no cout << "No\n"int ans = 0;
int treesize[5005];
vector<vector<int>> g(5005);
void dfs(int fa)
{treesize[fa] = 1;vector<int> sontreesize;for (auto & son : g[fa]){dfs(son);treesize[fa] += treesize[son];sontreesize.push_back(treesize[son]);}vector<int> f(5005, 0);f[0] = 1;int sum = 0;for (auto& sonsize : sontreesize){sum += sonsize;for (int i = sum; i >= sonsize; i--){f[i] |= f[i - sonsize];}}int mx = 0;for (int i = 0; i <= sum; i++){if (f[i]){mx = max(mx, i * (sum - i));}}ans += mx;
}void solve()
{int n;cin >> n;for (int i = 2; i <= n; i++){int fa; cin >> fa;g[fa].push_back(i);}dfs(1);cout << ans << endl;
}signed main()
{cin.tie(0)->sync_with_stdio(false);int t = 1;while (t--){solve();}return 0;
}相关文章:

【CF】Day72——Codeforces Round 890 (Div. 2) CDE1 (二分答案 | 交互 + 分治 | ⭐树上背包)
C. To Become Max 题目: 思路: 二分挺好想的,但是check有点不好写 看到最大值,试试二分,如果 x 可以,那么 x - 1 肯定也可以,所以具有单调性,考虑二分 如何check呢?由于…...

单片机寄存器的四种主要类型!
1. 控制寄存器(Control Registers) 专业定义:用于配置硬件行为或触发操作的寄存器。 大白话: 相当于设备的“控制面板”,通过写入特定值来开关功能或调整参数。例如&am…...

智能嗅探AJAX触发:机器学习在动态渲染中的创新应用
一、问题描述:数据加载变“隐形”,采集举步维艰 随着Web技术不断发展,越来越多网站采用了AJAX、动态渲染等技术来加载数据。以今日头条(https://www.toutiao.com)为例,用户打开网页时并不会一次性加载所有…...

【计算机网络】Linux下简单的UDP服务器(超详细)
套接字接口 我们把服务器封装成一个类,当我们定义出一个服务器对象后需要马上初始化服务器,而初始化服务器需要做的第一件事就是创建套接字。 🌎socket函数 这是Linux中创建套接字的系统调用,函数原型如下: int socket(int domain, int typ…...

Java并发编程实战 Day 3:volatile关键字与内存可见性
【Java并发编程实战 Day 3】volatile关键字与内存可见性 开篇 欢迎来到《Java并发编程实战》系列的第3天!本系列旨在带领你从基础到高级逐步掌握Java并发编程的核心概念和最佳实践。 今天我们将重点探讨volatile关键字及其在多线程程序中确保内存可见性的作用。我…...

华为OD机试真题——报文回路(2025A卷:100分)Java/python/JavaScript/C/C++/GO最佳实现
2025 A卷 100分 题型 本专栏内全部题目均提供Java、python、JavaScript、C、C++、GO六种语言的最佳实现方式; 并且每种语言均涵盖详细的问题分析、解题思路、代码实现、代码详解、3个测试用例以及综合分析; 本文收录于专栏:《2025华为OD真题目录+全流程解析+备考攻略+经验分…...

K8s工作流程与YAML实用指南
K8s 工作流程 K8s 采用声明式管理(用户说"要什么",K8s 负责"怎么做")方式,通过 YAML 文件描述期望的状态,K8s控制平面会自动确保实际状态与期望状态一致。 核心工作流程如下: 用户提交…...

功能丰富的PDF处理免费软件推荐
软件介绍 今天给大家介绍一款超棒的PDF工具箱,它处理PDF文档的能力超强,而且是完全免费使用的,没有任何限制。 TinyTools(PC)这款软件,下载完成后即可直接打开使用。在使用过程中,操作完毕后&a…...
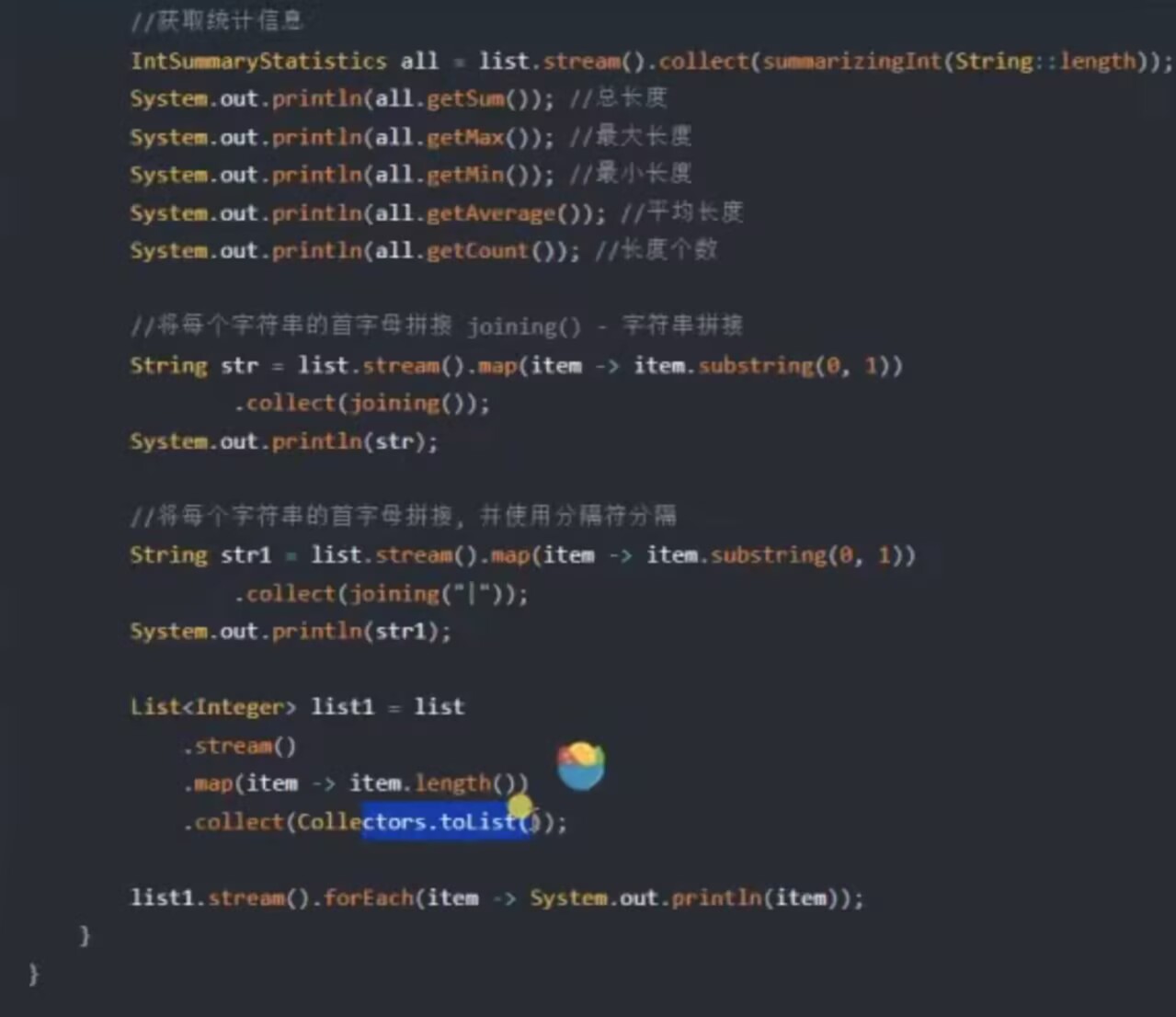
Java补充(Java8新特性)(和IO都很重要)
一、Lambda表达式 1.1、为什么使用Lambda表达式 Lambda表达式起步案例 下面源码注释是传统写法,代码是简写表达式写法 import java.util.ArrayList; import java.util.Collections; import java.util.Comparator; import java.util.function.Consumer;/* * 学什么…...

pycharm debug的时候无法debug到指定的位置就停住不动了
报错大致是这样的,但是直接run没有问题,debug就停住不动了 Traceback (most recent call last): File "/home/mapengsen/.pycharm_helpers/pydev/_pydevd_bundle/pydevd_comm.py", line 467, in start_client s.connect((host, port)) Timeou…...

分布式流处理与消息传递——Kafka ISR(In-Sync Replicas)算法深度解析
Java Kafka ISR(In-Sync Replicas)算法深度解析 一、ISR核心原理 #mermaid-svg-OQtnaUGNQ9PMgbW0 {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-OQtnaUGNQ9PMgbW0 .error-icon{fill:#55222…...

极大似然估计例题——正态分布的极大似然估计
设总体 X ∼ N ( μ , σ 2 ) X \sim N(\mu, \sigma^2) X∼N(μ,σ2),其中 μ \mu μ 和 σ 2 \sigma^2 σ2 是未知参数,取样本观测值为 x 1 , x 2 , ⋯ , x n x_1, x_2, \cdots, x_n x1,x2,⋯,xn,求参数 μ \mu μ 和 σ 2 \sigma^2 σ…...

Pull Request Integration 拉取请求集成
今天我想要把我创建的项目,通过修改yaml里面的内容,让我在main分支下的其他分支拉取请求的时候自动化测试拉取的内容,以及将测试结果上传到控制台云端。 首先我通过修改yaml文件里面的内容 name: Build and Teston:push:branches:- mainjobs:…...

OS10.【Linux】yum命令
目录 1.安装软件的几种方法 直接编译源代码,得到可执行程序 使用软件包管理器 2.yum yum list命令 参数解释 yum install命令 yum remove命令 下载链接存放的位置 扩展yum源 实验:安装sl小火车命令 sl命令的选项 方法1:man sl 方法2:读源代码 3.更新yum源 查看…...
)
头歌数据库课程实验(角色管理)
第1关:创建角色 任务描述 本关任务:创建角色 role1localhost。 相关知识 为了完成本关任务,你需要掌握MySQL的角色管理。 角色信息存放在数据库 mysql 的 user 表中。 user 表中字段: Host:可以登陆数据库的主机地…...

【android bluetooth 协议分析 03】【蓝牙扫描详解 1】【扫描关键函数 btif_dm_search_devices_evt 分析】
1. 背景 本篇我们来对 btif_dm_search_devices_evt 函数进行分析. 这是系统性分析 Bluetooth 协议栈中的设备扫描流程时必须厘清的一环。 1. 为什么要单独分析 btif_dm_search_devices_evt 函数: btif_dm_search_devices_evt 是 BTIF 层中处理设备扫描࿰…...

SpringBoot使用ThreadLocal保存登录用户信息
Java 多线程,系列文章: 《Java多线程》 《Java创建多线程的3种方法:继承Thread类、实现Runnable接口、实现Callable接口》 《Java多线程的同步:synchronized关键字、Lock接口、volatile关键字》 《Java线程池》 《Java线程池实现秒杀功能》 《SpringBoot使用ThreadLocal保存…...

多模态大语言模型arxiv论文略读(102)
Chat2Layout: Interactive 3D Furniture Layout with a Multimodal LLM ➡️ 论文标题:Chat2Layout: Interactive 3D Furniture Layout with a Multimodal LLM ➡️ 论文作者:Can Wang, Hongliang Zhong, Menglei Chai, Mingming He, Dongdong Chen, Ji…...
)
Ubuntu系统如何部署Crawlab爬虫管理平台(通过docker部署)
Ubuntu系统如何部署Crawlab爬虫管理平台(通过docker部署) 一、安装docker(ubuntu系统版本20.4) 1、更新apt sudo apt-get update2、安装必要的依赖包 sudo apt-get install ca-certificates curl gnupg lsb-release3、添加 Docker 官方 GPG 密钥(清化大学源) # 添加Docke…...
))
python常用库-pandas、Hugging Face的datasets库(大模型之JSONL(JSON Lines))
文章目录 python常用库pandas、Hugging Face的datasets库(大模型之JSONL(JSON Lines))背景什么是JSONL(JSON Lines)通过pandas读取和保存JSONL文件pandas读取和保存JSONL文件 Hugging Face的datasets库Hugg…...

高端装备制造企业如何选择适配的项目管理系统提升项目执行效率?附选型案例
高端装备制造项目通常涉及多专业协同、长周期交付和高风险管控,因此系统需具备全生命周期管理能力。例如,北京奥博思公司出品的 PowerProject 项目管理系统就是一款非常适合制造企业使用的项目管理软件系统。 国内某大型半导体装备制造企业与奥博思软件达…...

【Dv3Admin】工具权限配置文件解析
接口级权限控制是后台系统安全防护的核心手段。基于用户角色、请求路径与方法进行细粒度授权,可以有效隔离不同用户的数据访问范围,防止越权操作,保障系统整体稳定性。 本文解析 dvadmin/utils/permission.py 模块,重点关注其在匿…...

AI炼丹日志-22 - MCP 自动操作 Figma+Cursor 自动设计原型
MCP 基本介绍 官方地址: https://modelcontextprotocol.io/introduction “MCP 是一种开放协议,旨在标准化应用程序向大型语言模型(LLM)提供上下文的方式。可以把 MCP 想象成 AI 应用程序的 USB-C 接口。就像 USB-C 提供了一种…...
)
Python爬虫:AutoScraper 库详细使用大全(一个智能、自动、轻量级的网络爬虫)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、AutoScraper概述1.1 AutoScraper介绍1.2 安装1.3 注意事项二、基本使用方法2.1 创建 AutoScraper 实例2.2 训练模型2.3 保存和加载模型2.4 数据提取方法2.5 自定义规则三、高级功能3.1 多规则抓取3.2 分页抓取3.3 代…...

2025.6.1总结
今天又上了一天课,假期三天,上了两天的课,明天还得刷题。利用假期时间上课学习,并没有让我感到有多充实,反而让我感到有些小压抑。 在下午的好消息分享环节,我分享了毕业工作以来的一些迷茫。我不知道自己…...

[嵌入式实验]实验四:串口打印电压及温度
一、实验目的 熟悉开发环境在开发板上读取电压和温度信息使用串口和PC通信在PC上输出当前电压和温度信息 二、实验环境 硬件:STM32开发板、CMSIS-DAP调试工具 软件:STM32CubeMX软件、ARM的IDE:Keil C51 三、实验内容 配置相关硬件设施 &…...

LVS+Keepalived 高可用
目录 一、核心概念 1. LVS(Linux Virtual Server) 2. Keepalived 二、高可用架构设计 1. 架构拓扑图 2. 工作流程 三、部署步骤(以 DR 模式为例) 1. 环境准备 2. 主 LVS 节点配置 (1)安装 Keepali…...
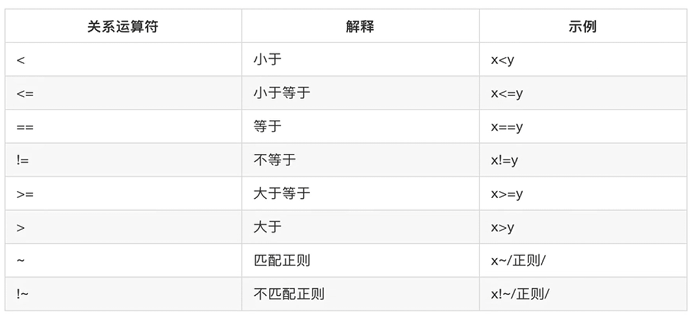
Linux正则三剑客篇
一、历史命令 history 命令 :用于输出历史上使用过的命令行数量及具体命令。通过 history 可以快速查看并回顾之前执行过的命令,方便重复操作或追溯执行过程。 !行号 :通过指定历史命令的行号来重新执行该行号对应的命令。例如,若…...

HTML5 视频播放器:从基础到进阶的实现指南
在现代Web开发中,视频播放功能是许多网站的重要组成部分。无论是在线教育平台、视频分享网站,还是企业官网,HTML5视频播放器都扮演着不可或缺的角色。本文将从基础到进阶,详细介绍如何实现一个功能完善的HTML5视频播放器ÿ…...
的实战教程)
鸿蒙HarmonyOS (React Native)的实战教程
一、环境配置 安装鸿蒙专属模板 bashCopy Code npx react-native0.72.5 init HarmonyApp --template react-native-template-harmony:ml-citation{ref"4,6" data"citationList"} 配置 ArkTS 模块路径 在 entry/src/main/ets 目录下创建原生模块&…...
