【LeetCode 热题100】动态规划实战:打家劫舍、完全平方数与零钱兑换(LeetCode 198 / 279 / 322)(Go语言版)
💰 动态规划实战:打家劫舍、完全平方数与零钱兑换(LeetCode 198 / 279 / 322)
本篇博客一次性带你掌握三道 LeetCode 中经典的动态规划(DP)题目:
- 🏠 198. 打家劫舍(House Robber)
- 🟩 279. 完全平方数(Perfect Squares)
- 💸 322. 零钱兑换(Coin Change)
它们覆盖了动态规划中的线性状态转移、完全背包问题,以及最小子结构决策问题。
🏠 一、198. 打家劫舍
📌 题目描述
一排房子,每个房子里有一定金额的钱,不能偷相邻的两个房子。求最多能偷多少钱?
💡 解题思路
这是一个典型的线性动态规划问题。
设 dp[i] 表示前 i 个房子最多能偷的钱:
- 偷第
i个房子 → 前i - 2个房子最大值 +nums[i] - 不偷第
i个房子 → 前i - 1个房子最大值
状态转移方程为:
dp[i] = max(dp[i-1], dp[i-2] + nums[i])
✅ Go 实现(空间优化版)
func rob(nums []int) int {if len(nums) == 0 {return 0}if len(nums) == 1 {return nums[0]}prev, curr := 0, 0for _, num := range nums {prev, curr = curr, max(curr, prev+num)}return curr
}func max(a, b int) int {if a > b {return a}return b
}
🟩 二、279. 完全平方数
📌 题目描述
给你一个整数
n,将其表示为若干个完全平方数的和,求这些数的最少数量。
💡 解题思路
这是一个典型的完全背包问题。
- 状态定义:
dp[i]表示组成i所需的最少平方数数量; - 状态转移:尝试每一个
j*j <= i的平方数:
dp[i] = min(dp[i], dp[i - j*j] + 1)
✅ Go 实现
func numSquares(n int) int {dp := make([]int, n+1)for i := 1; i <= n; i++ {dp[i] = i // 最坏情况:1+1+1+...+1for j := 1; j*j <= i; j++ {dp[i] = min(dp[i], dp[i - j*j] + 1)}}return dp[n]
}func min(a, b int) int {if a < b {return a}return b
}
💸 三、322. 零钱兑换
📌 题目描述
给定不同面额的硬币 coins 和总金额 amount,求最少的硬币数量使得总金额为 amount。如果没有一种组合能组成,返回 -1。
💡 解题思路
也是典型的完全背包问题,区别在于:
- 目标是最小硬币数
- 状态定义:
dp[i]表示组成金额i所需最少的硬币数 - 初始化:
dp[0] = 0,其余为inf(表示不可达)
状态转移方程:
dp[i] = min(dp[i], dp[i - coin] + 1)
✅ Go 实现
func coinChange(coins []int, amount int) int {dp := make([]int, amount+1)for i := 1; i <= amount; i++ {dp[i] = amount + 1}for _, coin := range coins {for i := coin; i <= amount; i++ {dp[i] = min(dp[i], dp[i - coin] + 1)}}if dp[amount] > amount {return -1}return dp[amount]
}
🔚 总结对比
| 题目 | 本质 | 状态定义 | 特点 |
|---|---|---|---|
| 打家劫舍 | 线性DP | dp[i] 表示前 i 间房最多可偷金额 | 不能连续取相邻元素 |
| 完全平方数 | 完全背包 | dp[i] 表示组成 i 所需的最少平方数个数 | 类似零钱兑换 |
| 零钱兑换 | 完全背包 | dp[i] 表示组成金额 i 最少硬币数 | 与完全平方数模型一致 |
📘 写在最后
这三道题虽然看起来背景完全不同,但本质上都属于一维动态规划问题,熟悉它们可以极大提升你解决复杂 DP 问题的能力。
建议继续练习类似题目:
-
- 打家劫舍 II(环形房屋)
-
- 三角形最小路径和
-
- 最长递增子序列
相关文章:
(Go语言版))
【LeetCode 热题100】动态规划实战:打家劫舍、完全平方数与零钱兑换(LeetCode 198 / 279 / 322)(Go语言版)
💰 动态规划实战:打家劫舍、完全平方数与零钱兑换(LeetCode 198 / 279 / 322) 本篇博客一次性带你掌握三道 LeetCode 中经典的动态规划(DP)题目: 🏠 198. 打家劫舍(Hou…...
换ip是换网络的意思吗?怎么换ip地址
在数字化时代,IP地址作为我们在网络世界的"身份证",其重要性不言而喻。许多人常将"换IP"与"换网络"混为一谈,实际上两者虽有联系却存在本质区别。本文将澄清这一概念误区,并详细介绍多种更换IP地址…...

【软件】在 macOS 上安装 MySQL
在 macOS 上安装 MySQL 有多种方法,以下是两种常见的安装方式:通过 Homebrew 安装和通过安装包安装。以下是详细的步骤: 一、通过 Homebrew 安装 MySQL Homebrew 是 macOS 的包管理器,使用它安装 MySQL 非常方便。 1.安装 Home…...

手机归属地查询接口如何用Java调用?
一、什么是手机归属地查询接口? 是一种便捷、高效的工具,操作简单,请求速度快。它不仅能够提高用户填写地址的效率,还能帮助企业更好地了解客户需求,制定个性化的营销策略,降低风险。随着移动互联网的发展…...

随笔20250530 C# 整合 IC卡读写技术解析与实现
以下是一个完整、最简化的 FeliCa 读取整合示例(无需 SDK,基于 PCSC NuGet 包),你可以直接运行这个控制台程序,验证能否识别 RC-S300 并读取卡片 UID: 🧪 示例说明 📦 使用 NuGet 包…...
:为什么它能处理时序数据?它真的能减轻过拟合吗?)
循环神经网络(RNN):为什么它能处理时序数据?它真的能减轻过拟合吗?
循环神经网络(RNN):为什么它能处理时序数据?它真的能减轻过拟合吗? 在深度学习领域,循环神经网络(RNN, Recurrent Neural Network)是一种非常重要的神经网络结构,尤其适…...

JVM与JMM深度解析:从Java 8到Java 21的演进
文章目录 第一部分:JVM基础概念与架构JVM是什么?JVM整体架构运行时数据区类加载机制执行引擎 第二部分:Java内存模型(JMM)什么是Java内存模型JMM的核心问题主内存与工作内存内存间交互操作重排序与happens-before原则v…...

基于爬取的典籍数据重新设计前端界面
1.BooksView(书籍列表页) 2.ClassicsView(目录页) 3.管理员端...

基于C++的IOT网关和平台5:github项目ctGateway开发指南
初级代码游戏的专栏介绍与文章目录-CSDN博客 我的github:codetoys,所有代码都将会位于ctfc库中。已经放入库中我会指出在库中的位置。 这些代码大部分以Linux为目标但部分代码是纯C++的,可以在任何平台上使用。 源码指引:github源码指引_初级代码游戏的博客-CSDN博客 系…...

揭秘 NextJS Script 组件
揭秘 NextJS Script 组件 Next.js 的 Script 组件是对原生 <script> 标签的增强封装,主要区别和优势如下: 自动优化加载策略(支持按需/延迟加载)避免重复加载内置性能优化(如预加载、回调钩子)简化…...

网络安全防御指南:全方位抵御暴力破解攻击
在数字化时代,网络安全威胁如影随形,暴力破解攻击(又称“爆破”)作为黑客常用的入侵手段,正时刻觊觎着系统的薄弱环节。想象一下,攻击者如同不知疲倦的“数字小偷”,利用自动化工具疯狂尝试成千…...

【C++/Linux】TinyWebServer前置知识之IP协议详解
目录 IPv4地址 分类 IP数据报分片 IP 协议在传输数据报时,将数据报分为若干分片(小数据报)后进行传输,并在目的系统中进行重组,这一过程称为分片(Fragmentation)。 IP模块工作流程编辑 I…...

mac安装brew时macos无法信任ruby的解决方法
背景 在使用如下脚本安装brew时,遇到安装ruby,macos不信任外部软件,在安全性点击信任仍然无法安装。 /bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/HEAD/install.sh)"如何解决 本地安装好符…...
Codeforces Round 1028 (Div. 2)(A-D)
题面链接:Dashboard - Codeforces Round 1028 (Div. 2) - Codeforces A. Gellyfish and Tricolor Pansy 思路 要知道骑士如果没了那么这个人就失去了攻击手段,贪心的来说我们只需要攻击血量少的即可,那么取min比较一下即可 代码 void so…...

记录一个梦,借助大语言模型图片生成
梦见家门口有一条大河,但大河和其它景物都是灰暗没有鲜艳色彩很普通的梦中场景。大河似乎是长江的支流,但也可能有一个响亮的名字似乎是金沙江。 突然看到一条金红色的龙在快速游动,不敢相信自己的眼睛,因为一直不相信有这种生物…...
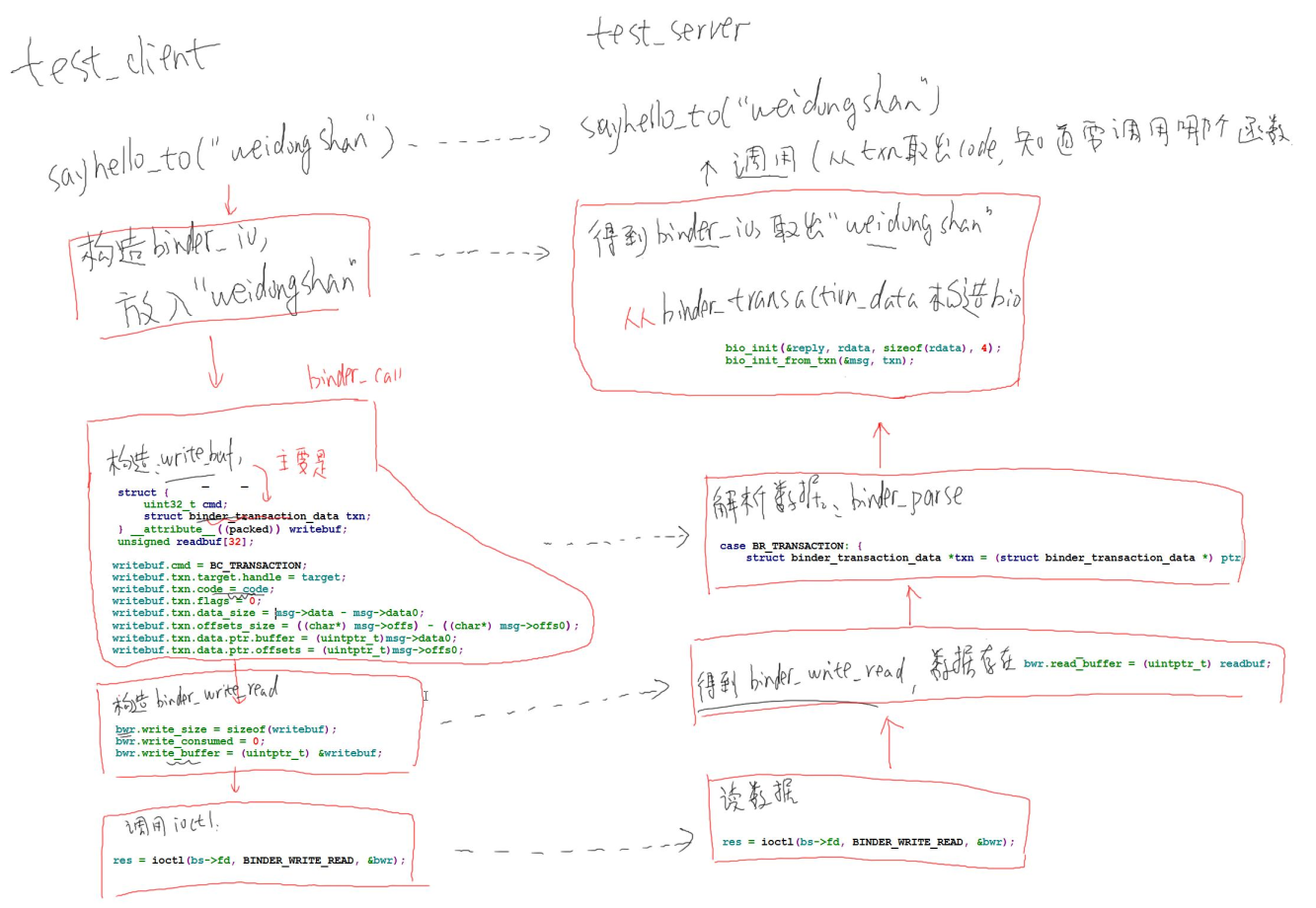
android binder(二)应用层编程实例
一、binder驱动浅析 从上图看出,binder的通讯主要涉及三个步骤。 在 Binder Server 端定义好服务,然后向 ServiceManager 注册服务在 Binder Client 中向 ServiceManager 获取到服务发起远程调用,调用 Binder Server 中定义好的服务 整个流…...

HTML 等价字符引用:系统化记忆指南
HTML 等价字符引用:系统化记忆指南 在 HTML 中,字符引用(Character Entity References)用于表示保留字符或特殊符号。我将提供一个系统化的方法来记忆这些重要实体,并解释它们的实际应用。 什么是等价字符引用? HTML 字符引用有两种形式: 命名实体:&entity_name…...

【深度学习】17. 深度生成模型:DCGAN与Wasserstein GAN公式深度推导
深度生成模型:DCGAN与Wasserstein GAN公式深度推导 深度卷积生成对抗网络 DCGAN 在原始 GAN 框架中,生成器和判别器通常使用全连接层构建,这限制了模型处理图像的能力。为此,Radford 等人在 2016 年提出了 DCGAN(Deep Convoluti…...

Ubuntu终端性能监视工具
目录 工具1:nvidia-smi 工具2:nvtop 工具3:nvitop 工具1:nvidia-smi nvidia-smi 如果希望自动刷新这个命令,可以输入如下命令: nvidia-smi -l 工具2:nvtop nvtop 安装方法: …...

设计模式——命令设计模式(行为型)
摘要 本文介绍了命令设计模式,这是一种行为型设计模式,用于将请求封装为对象,实现请求的解耦和灵活控制。它包含命令接口、具体命令、接收者、调用者和客户端等角色,优点是解耦请求发送者与接收者,支持命令的排队、记…...

鸿蒙OSUniApp智能商品展示实战:打造高性能的动态排序系统#三方框架 #Uniapp
UniApp智能商品展示实战:打造高性能的动态排序系统 引言 在电商应用开发中,商品展示和智能排序是提升用户体验的关键因素。随着HarmonyOS生态的发展,用户对应用的性能和交互体验要求越来越高。本文将深入探讨如何在UniApp中实现一个性能优异…...

03 APP 自动化-定位元素工具元素定位
文章目录 一、Appium常用元素定位工具1、U IAutomator View Android SDK 自带的定位工具2、Appium Desktop Inspector3、Weditor安装:Weditor工具的使用 4、uiautodev通过定位工具获取app页面元素有哪些属性 二、app 元素定位方法 一、Appium常用元素定位工具 1、U…...

PABD 2025:大数据与智慧城市管理的融合之道
会议简介 2025年公共管理与大数据国际会议(ICPMBD 2025)确实在海口举办。本次会议将围绕公共管理与大数据的深度融合、数据分析在公共管理中的应用、大数据驱动的政策制定与优化等议题展开深入研讨。参会者将有机会聆听前沿学术报告,分享研究…...

Golang持续集成与自动化测试和部署
概述 Golang是一门性能优异的静态类型语言,但因其奇快的编译速度,结合DevOps, 使得它也非常适合快速开发和迭代。 本文讲述如何使用Golang, 进行持续集成与自动化测试和部署。主要使用了以下相关技术: dep: 进行包的依赖管理gin…...

三套知识系统的实践比较:Notion、Confluence 与 Gitee Wiki
在过去几年中,我们团队先后使用过三套企业知识系统:Notion、Confluence 和 Gitee Wiki。每一套系统上线初期都带来一阵热情,但最终能真正融入研发流程、持续活跃的,只有最后一个。 我们不是要为某个平台背书,而是希望…...

mysql离线安装教程
1.下载地址: https://downloads.mysql.com/archives/community/ 2.上传安装包到系统目录,并解压 tar -xvf mysql-8.0.34-1.el7.x86_64.rpm-bundle.tar3.检查系统中是否存在mariadb的rpm包 rpm -qa|grep mariadb存在则删除 rpm -e xxx4.解压完后执行如下命令安装 sudo rpm -iv…...

OpenGL 3D 编程
OpenGL 是一个强大的跨平台图形 API,用于渲染 2D 和 3D 图形。以下是 OpenGL 3D 编程的入门基础。 一. 环境设置 安装必要的库 GLFW: 用于创建窗口和处理输入 GLEW 或 GLAD: 用于加载 OpenGL 函数 GLM: 数学库,用于 3D 变换 // 基本 OpenGL 程序结构示例 #include <GL/g…...

基于FPGA的VGA显示文字和动态数字基础例程,进而动态显示数据,类似温湿度等
基于FPGA的VGA显示文字和数字 前言一、VGA显示参数二、字模生成三、代码分析1.vga_char顶层2.vga_ctrl驱动文件3.vga_pic数据准备文件 总结 前言 结合正点原子以及野火的基础例程,理解了VGA本身基本协议,VGA本身显示像素为640*480,因此注意生…...

力扣刷题Day 68:搜索插入位置(35)
1.题目描述 2.思路 方法1:回溯的二分查找。 方法2:看到了一个佬很简洁的写法,代码贴在下面了。 3.代码(Python3) 方法1: class Solution:def searchInsert(self, nums: List[int], target: int) ->…...

NodeJS全栈WEB3面试题——P4Node.js后端集成 服务端设计
4.1 如何在 Node.js 中管理钱包与私钥的安全性? 私钥管理原则:不暴露,不硬编码,不明文存储。 常见做法: 加密存储: 使用 crypto 或 ethers.Wallet.encrypt() 加密私钥,存储到数据库或文件系统…...
