【深度学习】17. 深度生成模型:DCGAN与Wasserstein GAN公式深度推导
深度生成模型:DCGAN与Wasserstein GAN公式深度推导
深度卷积生成对抗网络 DCGAN
在原始 GAN 框架中,生成器和判别器通常使用全连接层构建,这限制了模型处理图像的能力。为此,Radford 等人在 2016 年提出了 DCGAN(Deep Convolutional GANs),将 CNN 架构引入 GAN 系统,在图像生成任务中取得巨大成功。
DCGAN 的网络结构

DCGAN 仍然包括两个模块:
-
生成器(Generator):
- 输入为一个随机向量 z z z,通常为 z ∼ N ( 0 , 1 ) z \sim \mathcal{N}(0, 1) z∼N(0,1);
- 通过一系列反卷积(Fractional Strided Convolutions / Transposed Convolutions)层将低维噪声向量逐步上采样为图像;
- 输出图像维度如 64 × 64 × 3 64 \times 64 \times 3 64×64×3。
-
判别器(Discriminator):
- 接收图像(真实或伪造)作为输入;
- 通过一系列普通卷积(strided convolutions)和 LeakyReLU 激活函数进行下采样;
- 最后输出一个标量,表示输入图像为“真实图像”的概率。
图中展示了典型 DCGAN 结构:
- 左侧:生成器网络,逐步上采样生成图像;
- 右侧:判别器网络,逐步提取图像特征进行判断;
- 右上角还展示了反卷积(Transposed Convolution)过程,直观说明如何将小尺寸特征图恢复成大尺寸图像。
DCGAN 的设计原则(五条黄金法则)
-
去除所有池化层(Pooling):
-
strided convolutions (discriminator) and fractional-strided convolutions (generator)
-
在生成器中使用 Fractional Strided Convolution(即反卷积)进行上采样;
-
在判别器中使用 Strided Convolution 进行下采样。
-
-
在生成器和判别器中都使用 Batch Normalization:
- 有助于稳定训练;
- 防止梯度消失;
- 加速收敛。
-
移除所有全连接隐藏层(fully-connected hidden layers):
- 简化网络结构;
- 提升可扩展性与泛化能力。
-
激活函数设计:
- 在生成器中,除了最后一层使用 Tanh,其余各层都使用 ReLU 激活;
- 在判别器中,所有层都使用 LeakyReLU 激活,避免死神经。
-
输出范围规范化:
- 生成器输出图像通过 Tanh 映射到 [ − 1 , 1 ] [-1, 1] [−1,1];
- 因此训练图像也需要归一化处理至 [ − 1 , 1 ] [-1, 1] [−1,1]。
总结
DCGAN 通过引入卷积结构,使得 GAN 在图像领域具备更强建模能力:
- 支持大尺寸图像生成;
- 图像更加平滑、连贯、有结构;
- 训练更稳定,调参更容易;
- 为后续诸如 StyleGAN、Pix2Pix 等强大 GAN 模型奠定了基础。
来源于 Radford 等人发表于 ICLR 2016 的经典论文:
“Unsupervised Representation Learning with Deep Convolutional GANs”
GAN 的核心训练难题:梯度消失(Gradient Vanishing)
尽管 DCGAN 等架构提升了稳定性,但生成对抗网络在训练早期仍然面临一个经典难题:梯度消失问题(vanishing gradient)。
原始目标函数
判别器的训练目标为:
J ( D ) = − E x ∼ p r [ log D ( x ) ] − E x ∼ p g [ log ( 1 − D ( x ) ) ] J^{(D)} = -\mathbb{E}_{x \sim p_r}[\log D(x)] - \mathbb{E}_{x \sim p_g}[\log(1 - D(x))] J(D)=−Ex∼pr[logD(x)]−Ex∼pg[log(1−D(x))]
生成器的训练目标为:
J ( G ) = E x ∼ p g [ log ( 1 − D ( x ) ) ] J^{(G)} = \mathbb{E}_{x \sim p_g}[\log(1 - D(x))] J(G)=Ex∼pg[log(1−D(x))]
生成器尝试最大化 D ( G ( z ) ) D(G(z)) D(G(z)),使得判别器误判其为真实图像。
为什么会发生梯度消失?
在训练初期,生成器 G G G生成的图像往往非常粗糙,不具备真实数据的特征。此时:
- 判别器 D D D很容易分辨出 G ( z ) G(z) G(z)是伪造的;
- 因此 D ( G ( z ) ) ≈ 0 D(G(z)) \approx 0 D(G(z))≈0;
- 那么 log ( 1 − D ( G ( z ) ) ) ≈ 0 \log(1 - D(G(z))) \approx 0 log(1−D(G(z)))≈0,梯度也几乎为零;
- 生成器难以获得有效的梯度信号进行优化。
本质悖论
In GAN, better discriminator leads to worse vanishing gradient in its generator!
- 判别器越强,训练越快,越容易压垮生成器;
- 生成器越弱,收到的训练信号越微弱;
- 双方很难在初期同步进步,导致训练不稳定。
1. 原始 GAN 判别器的最优目标函数推导
我们先从 GAN 中判别器 D D D 的原始损失函数出发:
J ( D ) = − E x ∼ p r [ log D ( x ) ] − E x ∼ p g [ log ( 1 − D ( x ) ) ] J^{(D)} = -\mathbb{E}_{x \sim p_r}[\log D(x)] - \mathbb{E}_{x \sim p_g}[\log(1 - D(x))] J(D)=−Ex∼pr[logD(x)]−Ex∼pg[log(1−D(x))]
这是判别器试图最大化其“判断正确”的期望值:
- 第一项:希望对真实样本 x ∼ p r x \sim p_r x∼pr 输出 D ( x ) D(x) D(x) 尽可能大(接近 1);
- 第二项:希望对生成样本 x ∼ p g x \sim p_g x∼pg 输出 D ( x ) D(x) D(x) 尽可能小(接近 0)。
我们将 J ( D ) J^{(D)} J(D) 看作对 D ( x ) D(x) D(x) 的函数,在每个点 x x x 上独立求偏导并令其为 0,即可求出最优判别器。
2. 最优判别器 D ∗ ( x ) D^*(x) D∗(x) 的解析表达式
当 J ( D ) J^{(D)} J(D) 取极大值时,对每个 x x x,最优解满足:
∂ J ( D ) ∂ D ( x ) = − p r ( x ) D ( x ) + p g ( x ) 1 − D ( x ) = 0 \frac{\partial J^{(D)}}{\partial D(x)} = -\frac{p_r(x)}{D(x)} + \frac{p_g(x)}{1 - D(x)} = 0 ∂D(x)∂J(D)=−D(x)pr(x)+1−D(x)pg(x)=0
d d x log x = 1 x \frac{d}{dx} \log x = \frac{1}{x} dxdlogx=x1
解该方程可得:
D ∗ ( x ) = p r ( x ) p r ( x ) + p g ( x ) D^*(x) = \frac{p_r(x)}{p_r(x) + p_g(x)} D∗(x)=pr(x)+pg(x)pr(x)
这表明,最优判别器会根据两个分布的相对概率密度比值来输出真实的可能性概率。
例如:
- 若 p r ( x ) ≫ p g ( x ) p_r(x) \gg p_g(x) pr(x)≫pg(x),说明该点 x x x 更可能来自真实数据, D ∗ ( x ) → 1 D^*(x) \to 1 D∗(x)→1;
- 若 p g ( x ) ≫ p r ( x ) p_g(x) \gg p_r(x) pg(x)≫pr(x),说明该点更可能是伪造的, D ∗ ( x ) → 0 D^*(x) \to 0 D∗(x)→0;
- 若两者相等, D ∗ ( x ) = 0.5 D^*(x) = 0.5 D∗(x)=0.5,即判别器无法判断。
3. 生成器目标函数下的 JS 散度
在 GAN 中,生成器的原始损失为:
J ( G ) = E x ∼ p g [ log ( 1 − D ( x ) ) ] J^{(G)} = \mathbb{E}_{x \sim p_g}[\log(1 - D(x))] J(G)=Ex∼pg[log(1−D(x))]
若将最优判别器 D ∗ ( x ) D^*(x) D∗(x) 代入,可得生成器最小化的目标函数为:
J ( G ) = E x ∼ p g [ log ( 1 − p r ( x ) p r ( x ) + p g ( x ) ) ] = E x ∼ p g [ log ( p g ( x ) p r ( x ) + p g ( x ) ) ] J^{(G)} = \mathbb{E}_{x \sim p_g} \left[\log\left(1 - \frac{p_r(x)}{p_r(x) + p_g(x)}\right)\right] = \mathbb{E}_{x \sim p_g} \left[\log\left(\frac{p_g(x)}{p_r(x) + p_g(x)}\right)\right] J(G)=Ex∼pg[log(1−pr(x)+pg(x)pr(x))]=Ex∼pg[log(pr(x)+pg(x)pg(x))]
该函数与下面这个表达式一同构成 GAN 最优判别器目标:
J ( D ∗ ) = 2 J S ( p r ∥ p g ) − 2 log 2 J^{(D^*)} = 2\,JS(p_r \| p_g) - 2\log 2 J(D∗)=2JS(pr∥pg)−2log2
即,在 D = D ∗ D=D^* D=D∗ 时,GAN 的优化等价于最小化真实分布 p r p_r pr 与生成分布 p g p_g pg 之间的 Jensen-Shannon 散度(JS divergence)。
4. Jensen-Shannon 散度的定义
JS 散度是衡量两个概率分布相似度的一种对称度量方式,定义为:
J S ( p ∥ q ) = 1 2 K L ( p ∥ m ) + 1 2 K L ( q ∥ m ) JS(p \| q) = \frac{1}{2}KL(p \| m) + \frac{1}{2}KL(q \| m) JS(p∥q)=21KL(p∥m)+21KL(q∥m)
其中, m ( x ) m(x) m(x) 是 p p p 和 q q q 的平均分布:
m ( x ) = 1 2 ( p ( x ) + q ( x ) ) m(x) = \frac{1}{2}(p(x) + q(x)) m(x)=21(p(x)+q(x))
而 KL 散度(Kullback-Leibler Divergence)为:
K L ( p ∥ q ) = − ∑ x p ( x ) log ( q ( x ) p ( x ) ) KL(p \| q) = -\sum_x p(x) \log\left(\frac{q(x)}{p(x)}\right) KL(p∥q)=−x∑p(x)log(p(x)q(x))
特性:
- JS 散度值域在 [ 0 , log 2 ] [0, \log 2] [0,log2];
- JS 散度为 0 当且仅当 p = q p = q p=q;
- 若 p p p 和 q q q 的支持集无交集,则 J S ( p ∥ q ) = log 2 JS(p \| q) = \log 2 JS(p∥q)=log2;
- JS 散度的梯度在边界处为 0,这会导致训练困难(梯度消失)。
推导说明:为什么有
V ( D ∗ , G ) = K L ( p r ∥ m ) + K L ( p g ∥ m ) − 2 log 2 V(D^*, G) = KL(p_r \| m) + KL(p_g \| m) - 2 \log 2 V(D∗,G)=KL(pr∥m)+KL(pg∥m)−2log2
背景:我们从最优判别器的对抗损失出发:
V ( D ∗ , G ) = E x ∼ p r [ log ( p r ( x ) p r ( x ) + p g ( x ) ) ] + E x ∼ p g [ log ( p g ( x ) p r ( x ) + p g ( x ) ) ] V(D^*, G) = \mathbb{E}_{x \sim p_r} \left[ \log \left( \frac{p_r(x)}{p_r(x) + p_g(x)} \right) \right] + \mathbb{E}_{x \sim p_g} \left[ \log \left( \frac{p_g(x)}{p_r(x) + p_g(x)} \right) \right] V(D∗,G)=Ex∼pr[log(pr(x)+pg(x)pr(x))]+Ex∼pg[log(pr(x)+pg(x)pg(x))]关键技巧:定义中间分布:
m ( x ) = 1 2 ( p r ( x ) + p g ( x ) ) ⇒ p r ( x ) + p g ( x ) = 2 m ( x ) m(x) = \frac{1}{2}(p_r(x) + p_g(x)) \quad \Rightarrow \quad p_r(x) + p_g(x) = 2m(x) m(x)=21(pr(x)+pg(x))⇒pr(x)+pg(x)=2m(x)换分母:
p r ( x ) p r ( x ) + p g ( x ) = p r ( x ) 2 m ( x ) , p g ( x ) p r ( x ) + p g ( x ) = p g ( x ) 2 m ( x ) \frac{p_r(x)}{p_r(x) + p_g(x)} = \frac{p_r(x)}{2m(x)}, \quad \frac{p_g(x)}{p_r(x) + p_g(x)} = \frac{p_g(x)}{2m(x)} pr(x)+pg(x)pr(x)=2m(x)pr(x),pr(x)+pg(x)pg(x)=2m(x)pg(x)带入期望后:
V ( D ∗ , G ) = E x ∼ p r [ log ( p r ( x ) 2 m ( x ) ) ] + E x ∼ p g [ log ( p g ( x ) 2 m ( x ) ) ] V(D^*, G) = \mathbb{E}_{x \sim p_r} \left[ \log \left( \frac{p_r(x)}{2m(x)} \right) \right] + \mathbb{E}_{x \sim p_g} \left[ \log \left( \frac{p_g(x)}{2m(x)} \right) \right] V(D∗,G)=Ex∼pr[log(2m(x)pr(x))]+Ex∼pg[log(2m(x)pg(x))]拆开 log \log log 用恒等式:
log ( p ( x ) 2 m ( x ) ) = log ( p ( x ) m ( x ) ) − log 2 \log \left( \frac{p(x)}{2m(x)} \right) = \log \left( \frac{p(x)}{m(x)} \right) - \log 2 log(2m(x)p(x))=log(m(x)p(x))−log2log ( a b ) = log a − log b \log \left( \frac{a}{b} \right) = \log a - \log b log(ba)=loga−logb
所以:
V ( D ∗ , G ) = K L ( p r ∥ m ) + K L ( p g ∥ m ) − 2 log 2 V(D^*, G) = KL(p_r \| m) + KL(p_g \| m) - 2 \log 2 V(D∗,G)=KL(pr∥m)+KL(pg∥m)−2log2小结:对抗损失在 D ∗ D^* D∗ 时,等价于:
V ( D ∗ , G ) = 2 ⋅ J S ( p r ∥ p g ) − 2 log 2 V(D^*, G) = 2 \cdot JS(p_r \| p_g) - 2 \log 2 V(D∗,G)=2⋅JS(pr∥pg)−2log2也就是说:GAN 实际上在最小化 JS 散度
5. 支持集不重叠时的问题
如图所示:

- 图 A:两个分布完全不重叠, J S = log 2 JS = \log 2 JS=log2;
- 图 B:两者有轻微重叠,JS 仍较大。
在这种情况下, J ( G ) J^{(G)} J(G) 的梯度为 0:
∇ θ g J ( G ) = 0 \nabla_{\theta_g} J^{(G)} = 0 ∇θgJ(G)=0
这意味着:生成器无法收到任何学习信号!
这是原始 GAN 的根本性问题所在。
图 A:无重叠的支持集
-
红色区域代表真实数据的概率密度 p r ( x ) p_r(x) pr(x);
-
黄色区域代表生成器生成的数据密度 p g ( x ) p_g(x) pg(x);
-
二者没有任何交集(支持集 disjoint):
supp ( p r ) ∩ supp ( p g ) = ∅ \text{supp}(p_r) \cap \text{supp}(p_g) = \varnothing supp(pr)∩supp(pg)=∅
-
此时最优判别器为:
D ∗ ( x ) = { 1 x ∈ supp ( p r ) 0 x ∈ supp ( p g ) D^*(x) = \begin{cases} 1 & x \in \text{supp}(p_r) \\ 0 & x \in \text{supp}(p_g) \end{cases} D∗(x)={10x∈supp(pr)x∈supp(pg)
- 对于 K L ( p ∣ m ) KL(p | m) KL(p∣m):
仅在 p ( x ) > 0 p(x) > 0 p(x)>0 的地方有贡献,此时 m ( x ) = 1 2 p ( x ) m(x) = \frac{1}{2}p(x) m(x)=21p(x),所以:
K L ( p ∥ m ) = ∑ x ∈ supp ( p ) p ( x ) log ( p ( x ) 1 2 p ( x ) ) = ∑ x ∈ supp ( p ) p ( x ) log 2 = log 2 KL(p \| m) = \sum_{x \in \text{supp}(p)} p(x) \log \left( \frac{p(x)}{\frac{1}{2}p(x)} \right) = \sum_{x \in \text{supp}(p)} p(x) \log 2 = \log 2 KL(p∥m)=∑x∈supp(p)p(x)log(21p(x)p(x))=∑x∈supp(p)p(x)log2=log2
因为 ∑ x ∈ supp ( p ) p ( x ) = 1 \sum_{x \in \text{supp}(p)} p(x) = 1 ∑x∈supp(p)p(x)=1。
-
导致 V ( D ∗ , G ) = 2 ⋅ log 1 2 = − 2 log 2 V(D^*, G) = 2 \cdot \log \frac{1}{2} = -2 \log 2 V(D∗,G)=2⋅log21=−2log2,即:
J S ( p r ∥ p g ) = log 2 JS(p_r \| p_g) = \log 2 JS(pr∥pg)=log2因为 JS 散度已达最大值,其导数(梯度)为 0,生成器 无法获得有效梯度,这就是梯度消失问题的本质。
图 B:轻微重叠的支持集
-
真实分布和生成分布有部分重叠:
supp ( p r ) ∩ supp ( p g ) ≠ ∅ \text{supp}(p_r) \cap \text{supp}(p_g) \neq \varnothing supp(pr)∩supp(pg)=∅
-
在重叠区域中, D ∗ ( x ) D^*(x) D∗(x) 不再是 0 或 1,而是一个概率:
D ∗ ( x ) = p r ( x ) p r ( x ) + p g ( x ) ∈ ( 0 , 1 ) D^*(x) = \frac{p_r(x)}{p_r(x) + p_g(x)} \in (0,1) D∗(x)=pr(x)+pg(x)pr(x)∈(0,1)
-
因此:
J S ( p r ∥ p g ) < log 2 JS(p_r \| p_g) < \log 2 JS(pr∥pg)<log2
梯度 ∇ θ g J ( G ) \nabla_{\theta_g} J^{(G)} ∇θgJ(G) 不再为零,生成器可以继续更新。
公式结合解释
从前面的推导我们知道:
V ( D ∗ , G ) = 2 ⋅ J S ( p r ∥ p g ) − 2 log 2 V(D^*, G) = 2 \cdot JS(p_r \| p_g) - 2 \log 2 V(D∗,G)=2⋅JS(pr∥pg)−2log2
- 图 A: J S ( p r ∥ p g ) = log 2 ⇒ V = − 2 log 2 JS(p_r \| p_g) = \log 2 \Rightarrow V = -2 \log 2 JS(pr∥pg)=log2⇒V=−2log2,梯度消失;
- 图 B: J S ( p r ∥ p g ) < log 2 ⇒ V > − 2 log 2 JS(p_r \| p_g) < \log 2 \Rightarrow V > -2 \log 2 JS(pr∥pg)<log2⇒V>−2log2,仍有学习信号。
Wasserstein GAN :从距离度量到训练对抗目标的革新
什么是分布距离?
为度量两个概率分布 P P P 和 Q Q Q 的差异,常见方法包括:
-
KL 散度(Kullback–Leibler divergence):
K L ( P ∥ Q ) = ∑ x P ( x ) log ( P ( x ) Q ( x ) ) KL(P \| Q) = \sum_x P(x) \log \left( \frac{P(x)}{Q(x)} \right) KL(P∥Q)=x∑P(x)log(Q(x)P(x)) -
JS 散度(Jensen–Shannon divergence):
J S ( P ∥ Q ) = 1 2 K L ( P ∥ P + Q 2 ) + 1 2 K L ( Q ∥ P + Q 2 ) JS(P \| Q) = \frac{1}{2} KL\left(P \| \frac{P+Q}{2} \right) + \frac{1}{2} KL\left(Q \| \frac{P+Q}{2} \right) JS(P∥Q)=21KL(P∥2P+Q)+21KL(Q∥2P+Q) -
Wasserstein 距离(Earth-Mover Distance):
W ( P ∥ Q ) = inf γ ∈ Π ( P , Q ) E ( x , y ) ∼ γ [ ∥ x − y ∥ ] W(P \| Q) = \inf_{\gamma \in \Pi(P, Q)} \mathbb{E}_{(x, y) \sim \gamma}[\|x - y\|] W(P∥Q)=γ∈Π(P,Q)infE(x,y)∼γ[∥x−y∥]
其中 γ \gamma γ 是所有边缘分布分别为 P P P 和 Q Q Q 的联合分布集合 Π ( P , Q ) \Pi(P, Q) Π(P,Q)。可理解为:将 P P P 的质量“搬运”到 Q Q Q 所需的最小代价。
KL / JS / W 三种距离的对比示意
我们来考虑一个简单案例: P 1 P_1 P1 和 P 2 P_2 P2 是两个具有间隔 θ \theta θ 的分布。
| 距离类型 | 数学形式 | 特性 |
|---|---|---|
| K L ( P 1 ∣ P 2 ) KL(P_1 | P_2) KL(P1∣P2) | ∞ \infty ∞(若 θ ≠ 0 \theta \ne 0 θ=0);0(若 θ = 0 \theta = 0 θ=0) | 不连续;无梯度 |
| J S ( P 1 ∣ P 2 ) JS(P_1 | P_2) JS(P1∣P2) | log 2 \log 2 log2(若 θ ≠ 0 \theta \ne 0 θ=0);0(若 θ = 0 \theta = 0 θ=0) | 不连续;梯度为零 |
| W ( P 1 , P 2 ) W(P_1, P_2) W(P1,P2) | $ | \theta |
结论:Wasserstein 距离对分布支持集是否重叠不敏感,始终提供有用的梯度。
Wasserstein GAN 正式引入
WGAN 引入 Earth-Mover 距离作为衡量真实分布 P r P_r Pr 和生成分布 P g P_g Pg 的距离:
W ( P r , P g ) = inf γ ∈ Π ( P r , P g ) E ( x , y ) ∼ γ [ ∥ x − y ∥ ] W(P_r, P_g) = \inf_{\gamma \in \Pi(P_r, P_g)} \mathbb{E}_{(x, y) \sim \gamma}[\|x - y\|] W(Pr,Pg)=γ∈Π(Pr,Pg)infE(x,y)∼γ[∥x−y∥]
但由于直接优化该形式极其困难,WGAN 利用其对偶形式重写:
W ( P r , P g ) = sup ∥ f ∥ L ≤ 1 E x ∼ P r [ f ( x ) ] − E x ∼ P g [ f ( x ) ] W(P_r, P_g) = \sup_{\|f\|_L \le 1} \mathbb{E}_{x \sim P_r}[f(x)] - \mathbb{E}_{x \sim P_g}[f(x)] W(Pr,Pg)=∥f∥L≤1supEx∼Pr[f(x)]−Ex∼Pg[f(x)]
这里:
-
f f f 是一类满足 Lipschitz 条件的函数;
-
∥ f ∥ L ≤ 1 \|f\|_L \le 1 ∥f∥L≤1 表示 f f f 是 1-Lipschitz 连续函数;
∣ ∣ f ( x ) − f ( y ) ∣ ∣ ≤ ∥ x − y ∥ ||f(x) - f(y)|| \le \|x - y\| ∣∣f(x)−f(y)∣∣≤∥x−y∥
-
“supremum” 表示在所有满足条件的函数中取最大值。
对于更一般的 K-Lipschitz 函数( ∣ ∣ f ∣ ∣ L ≤ K ||f||_L \le K ∣∣f∣∣L≤K),有:
W ( P r , P g ) = 1 K sup ∥ f ∥ L ≤ K E x ∼ P r [ f ( x ) ] − E x ∼ P g [ f ( x ) ] W(P_r, P_g) = \frac{1}{K} \sup_{\|f\|_L \le K} \mathbb{E}_{x \sim P_r}[f(x)] - \mathbb{E}_{x \sim P_g}[f(x)] W(Pr,Pg)=K1∥f∥L≤KsupEx∼Pr[f(x)]−Ex∼Pg[f(x)]
什么是 K-Lipschitz 函数?
函数 f f f 是 K-Lipschitz 的含义为:
∥ f ( x ) − f ( y ) ∥ ≤ K ⋅ ∥ x − y ∥ 对所有 x , y 成立 \|f(x) - f(y)\| \le K \cdot \|x - y\| \quad \text{对所有 } x, y \text{ 成立} ∥f(x)−f(y)∥≤K⋅∥x−y∥对所有 x,y 成立
- 当 K = 1 K = 1 K=1,即为标准的 1-Lipschitz 函数;
- Lipschitz 条件确保 f f f 的梯度幅度不会过大,提供优化稳定性。
这个约束是 WGAN 成立的理论基础,也是后续训练中判别器(critic)要满足的重要条件。
用神经网络近似 Lipschitz 函数
为近似 Lipschitz 函数族 { f } \{f\} {f},WGAN 引入判别器(或称 critic) f w f_w fw,令其参数 w w w 落在某个约束空间中(如 w ∈ [ − c , c ] w \in [-c, c] w∈[−c,c]),以保证 f w f_w fw 是 Lipschitz。
最终形式为:
W ( P r , P g ) ≈ max w ∈ W E x ∼ P r [ f w ( x ) ] − E x ∼ P g [ f w ( x ) ] W(P_r, P_g) \approx \max_{w \in \mathcal{W}} \mathbb{E}_{x \sim P_r}[f_w(x)] - \mathbb{E}_{x \sim P_g}[f_w(x)] W(Pr,Pg)≈w∈WmaxEx∼Pr[fw(x)]−Ex∼Pg[fw(x)]
其中 W \mathcal{W} W 是所有 K K K-Lipschitz 参数的集合。
WGAN 做法:使用 weight clipping 强制 f w f_w fw 满足 Lipschitz 条件。
例如: W = [ − c , c ] l W =[−c, c]^l W=[−c,c]l为了满足这一要求,WGAN通过应用权值裁剪(weight clipping)来强制D在紧化空间[-c, c]中的权值
WGAN 的训练目标
判别器(Critic)优化目标:
L D = E x ∼ P r [ f w ( x ) ] − E x ∼ P g [ f w ( x ) ] \mathcal{L}_D = \mathbb{E}_{x \sim P_r}[f_w(x)] - \mathbb{E}_{x \sim P_g}[f_w(x)] LD=Ex∼Pr[fw(x)]−Ex∼Pg[fw(x)]
即最大化 Wasserstein 距离。
生成器优化目标:
L G = − E x ∼ P g [ f w ( x ) ] = − E z ∼ p ( z ) [ f w ( G ( z ) ) ] \mathcal{L}_G = -\mathbb{E}_{x \sim P_g}[f_w(x)] = -\mathbb{E}_{z \sim p(z)}[f_w(G(z))] LG=−Ex∼Pg[fw(x)]=−Ez∼p(z)[fw(G(z))]
即最小化 Wasserstein 距离。
WGAN 相比传统 GAN 的优势
| 指标 | 原始 GAN | WGAN |
|---|---|---|
| 判别器输出 | 概率(0~1) | 实值(任意实数) |
| 判别器损失 | JS 散度 | Wasserstein 距离 |
| 训练稳定性 | 极差,易崩 | 稳定,可控 |
| 梯度消失 | 常见 | 极少 |
WGAN 本质上是将原始 GAN 中的 JS 散度替换为 Wasserstein 距离,从而有效解决了梯度消失与训练不稳定的问题。
WGAN 训练算法流程
超参数设定
- α \alpha α:学习率(建议 5 × 10 − 5 5 \times 10^{-5} 5×10−5)
- c c c:权重裁剪边界(如 ± 0.01 \pm 0.01 ±0.01)
- m m m:每个批次的数据量(如 64)
- n critic n_{\text{critic}} ncritic:每次更新生成器前,critic 网络的更新次数(通常为 5)
整体流程
-
初始化参数:critic 的参数 w 0 w_0 w0,生成器参数 θ 0 \theta_0 θ0。
-
迭代训练:直到 θ \theta θ 收敛:
-
Step 1:更新 critic(判别器) n critic n_{\text{critic}} ncritic 次:
-
从真实数据分布 P r P_r Pr 中采样一个 minibatch { x ( i ) } \{x^{(i)}\} {x(i)};
-
从潜在分布 p ( z ) p(z) p(z) 中采样一组噪声 { z ( i ) } \{z^{(i)}\} {z(i)};
-
计算损失的梯度:
g w ← ∇ w [ 1 m ∑ i = 1 m f w ( x ( i ) ) − f w ( g θ ( z ( i ) ) ) ] g_w \leftarrow \nabla_w \left[ \frac{1}{m} \sum_{i=1}^m f_w(x^{(i)}) - f_w(g_\theta(z^{(i)})) \right] gw←∇w[m1i=1∑mfw(x(i))−fw(gθ(z(i)))] -
用 RMSProp 或 SGD 执行梯度上升:
w ← w + α ⋅ RMSProp ( w , g w ) w \leftarrow w + \alpha \cdot \text{RMSProp}(w, g_w) w←w+α⋅RMSProp(w,gw) -
执行 weight clipping:
w ← clip ( w , − c , c ) w \leftarrow \text{clip}(w, -c, c) w←clip(w,−c,c)
这一步保证 f w f_w fw 是 K-Lipschitz 函数(保持对偶形式成立)。
-
-
Step 2:更新生成器 G θ G_\theta Gθ 一次:
-
从噪声分布 p ( z ) p(z) p(z) 中采样 z ( i ) z^{(i)} z(i);
-
计算生成器梯度(负 critic 输出):
g θ ← − ∇ θ [ 1 m ∑ i = 1 m f w ( g θ ( z ( i ) ) ) ] g_\theta \leftarrow -\nabla_\theta \left[ \frac{1}{m} \sum_{i=1}^m f_w(g_\theta(z^{(i)})) \right] gθ←−∇θ[m1i=1∑mfw(gθ(z(i)))] -
执行梯度下降:
θ ← θ − α ⋅ RMSProp ( θ , g θ ) \theta \leftarrow \theta - \alpha \cdot \text{RMSProp}(\theta, g_\theta) θ←θ−α⋅RMSProp(θ,gθ)
-
-
有意义的损失指标(Meaningful Loss Metric)
GAN 的一个关键问题是:损失值是否能有效反映生成样本的质量?
Vanilla GAN 的问题
如下图所示,Vanilla GAN 使用 JS 散度(JSD estimate)作为训练目标,但其在训练过程中的表现不稳定且无法作为样本质量的衡量指标:
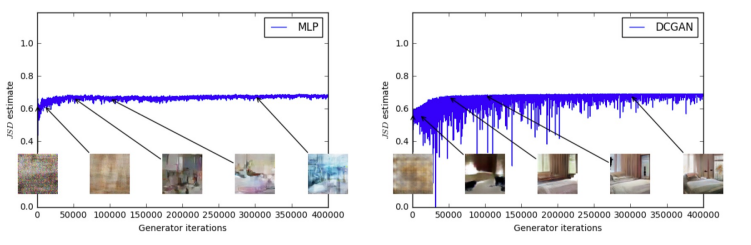
- 左图:MLP 生成器在训练过程中,生成样本逐渐变好,但 JSD 并没有显著下降。
- 右图:DCGAN 生成器样本质量明显提升,但 JSD 曲线波动剧烈,甚至略有上升。
结论:JSD 损失和样本质量之间没有明显的正相关性,因此 JSD 并不是一个有意义的训练指标。
WGAN 的优势
相比之下,WGAN 使用 Wasserstein 距离作为训练目标,其数值变化与生成样本的质量变化高度一致:

- 左图:MLP 生成器从模糊块逐渐生成清晰卧室图像,Wasserstein 距离稳定下降;
- 右图:DCGAN 同样表现出 Wasserstein 距离逐步收敛,与图像质量一致。
结论:WGAN 的损失函数具有实际意义,能够真实反映训练进度与样本质量。
相关文章:

【深度学习】17. 深度生成模型:DCGAN与Wasserstein GAN公式深度推导
深度生成模型:DCGAN与Wasserstein GAN公式深度推导 深度卷积生成对抗网络 DCGAN 在原始 GAN 框架中,生成器和判别器通常使用全连接层构建,这限制了模型处理图像的能力。为此,Radford 等人在 2016 年提出了 DCGAN(Deep Convoluti…...

Ubuntu终端性能监视工具
目录 工具1:nvidia-smi 工具2:nvtop 工具3:nvitop 工具1:nvidia-smi nvidia-smi 如果希望自动刷新这个命令,可以输入如下命令: nvidia-smi -l 工具2:nvtop nvtop 安装方法: …...

设计模式——命令设计模式(行为型)
摘要 本文介绍了命令设计模式,这是一种行为型设计模式,用于将请求封装为对象,实现请求的解耦和灵活控制。它包含命令接口、具体命令、接收者、调用者和客户端等角色,优点是解耦请求发送者与接收者,支持命令的排队、记…...

鸿蒙OSUniApp智能商品展示实战:打造高性能的动态排序系统#三方框架 #Uniapp
UniApp智能商品展示实战:打造高性能的动态排序系统 引言 在电商应用开发中,商品展示和智能排序是提升用户体验的关键因素。随着HarmonyOS生态的发展,用户对应用的性能和交互体验要求越来越高。本文将深入探讨如何在UniApp中实现一个性能优异…...

03 APP 自动化-定位元素工具元素定位
文章目录 一、Appium常用元素定位工具1、U IAutomator View Android SDK 自带的定位工具2、Appium Desktop Inspector3、Weditor安装:Weditor工具的使用 4、uiautodev通过定位工具获取app页面元素有哪些属性 二、app 元素定位方法 一、Appium常用元素定位工具 1、U…...

PABD 2025:大数据与智慧城市管理的融合之道
会议简介 2025年公共管理与大数据国际会议(ICPMBD 2025)确实在海口举办。本次会议将围绕公共管理与大数据的深度融合、数据分析在公共管理中的应用、大数据驱动的政策制定与优化等议题展开深入研讨。参会者将有机会聆听前沿学术报告,分享研究…...

Golang持续集成与自动化测试和部署
概述 Golang是一门性能优异的静态类型语言,但因其奇快的编译速度,结合DevOps, 使得它也非常适合快速开发和迭代。 本文讲述如何使用Golang, 进行持续集成与自动化测试和部署。主要使用了以下相关技术: dep: 进行包的依赖管理gin…...

三套知识系统的实践比较:Notion、Confluence 与 Gitee Wiki
在过去几年中,我们团队先后使用过三套企业知识系统:Notion、Confluence 和 Gitee Wiki。每一套系统上线初期都带来一阵热情,但最终能真正融入研发流程、持续活跃的,只有最后一个。 我们不是要为某个平台背书,而是希望…...

mysql离线安装教程
1.下载地址: https://downloads.mysql.com/archives/community/ 2.上传安装包到系统目录,并解压 tar -xvf mysql-8.0.34-1.el7.x86_64.rpm-bundle.tar3.检查系统中是否存在mariadb的rpm包 rpm -qa|grep mariadb存在则删除 rpm -e xxx4.解压完后执行如下命令安装 sudo rpm -iv…...

OpenGL 3D 编程
OpenGL 是一个强大的跨平台图形 API,用于渲染 2D 和 3D 图形。以下是 OpenGL 3D 编程的入门基础。 一. 环境设置 安装必要的库 GLFW: 用于创建窗口和处理输入 GLEW 或 GLAD: 用于加载 OpenGL 函数 GLM: 数学库,用于 3D 变换 // 基本 OpenGL 程序结构示例 #include <GL/g…...

基于FPGA的VGA显示文字和动态数字基础例程,进而动态显示数据,类似温湿度等
基于FPGA的VGA显示文字和数字 前言一、VGA显示参数二、字模生成三、代码分析1.vga_char顶层2.vga_ctrl驱动文件3.vga_pic数据准备文件 总结 前言 结合正点原子以及野火的基础例程,理解了VGA本身基本协议,VGA本身显示像素为640*480,因此注意生…...

力扣刷题Day 68:搜索插入位置(35)
1.题目描述 2.思路 方法1:回溯的二分查找。 方法2:看到了一个佬很简洁的写法,代码贴在下面了。 3.代码(Python3) 方法1: class Solution:def searchInsert(self, nums: List[int], target: int) ->…...

NodeJS全栈WEB3面试题——P4Node.js后端集成 服务端设计
4.1 如何在 Node.js 中管理钱包与私钥的安全性? 私钥管理原则:不暴露,不硬编码,不明文存储。 常见做法: 加密存储: 使用 crypto 或 ethers.Wallet.encrypt() 加密私钥,存储到数据库或文件系统…...

SQL进阶之旅 Day 12:分组聚合与HAVING高效应用
【SQL进阶之旅 Day 12】分组聚合与HAVING高效应用 在SQL的世界里,分组聚合(Grouping and Aggregation)是处理大规模数据集时最常用的技术之一。它允许我们将数据按照某些列进行分类,并对每个分类进行统计计算。而 HAVING 子句则是…...

深入剖析C#构造函数执行:基类调用、初始化顺序与访问控制
导言 在面向对象编程中,理解对象构造过程至关重要。C#的构造函数执行遵循严格的顺序规则,尤其是涉及继承和成员初始化时。本文将深入解析构造函数的执行流程、初始化语句的妙用以及类访问修饰符的影响,助你写出更健壮、可维护的代码。 构造…...

Java 大数据处理:使用 Hadoop 和 Spark 进行大规模数据处理
Java 大数据处理:使用 Hadoop 和 Spark 进行大规模数据处理 在当今数字化时代,数据呈现出爆炸式增长,如何高效地处理大规模数据成为企业面临的重要挑战。Java 作为一门广泛使用的编程语言,在大数据处理领域同样发挥着关键作用。本文将深入探讨如何利用 Hadoop 和 Spark 这…...

使用Python绘制节日祝福——以端午节和儿童节为例
端午节 端午节总算是回家了,感觉时间过得真快,马上就毕业了,用Python弄了一个端午节元素的界面,虽然有点不像,祝大家端午安康。端午节粽子(python)_python画粽子-CSDN博客https://blog.csdn.net…...
:参数量背后的“黄金公式”与Scaling Law的启示)
探索大语言模型(LLM):参数量背后的“黄金公式”与Scaling Law的启示
引言 过去十年,人工智能领域最震撼的变革之一,是模型参数量从百万级飙升至万亿级。从GPT-3的1750亿参数到GPT-4的神秘规模,再到谷歌Gemini的“多模态巨兽”,参数量仿佛成了AI能力的代名词。但参数真的是越多越好吗?这…...

Excel to JSON 插件 2.4.0 版本更新
我们很高兴地宣布 Excel to JSON 插件已升级到 2.4.0 版本!本次更新带来了两项重要功能,旨在为您提供更大的灵活性和更强大的数据处理能力。 主要更新内容: 1. 用户可以选择从行或列中选择标题 在之前的版本中,插件通常默认从第…...

黑马点评后端笔记
1.基于Session实现登录流程 发送验证码: 先前端校验,后端再校验(防小人),合法生成验证码(RandomUtil生成),后端保存,在通过短信去发送给用户 短信验证码登录和注册: 拿到验证码和手机号后,后端通过session(spring mvc注入)拿到验证码,进行校验,如果用户…...

C#项目07-二维数组的随机创建
实现需求 创建二维数组,数组的列和宽为随机,数组内的数也是随机 知识点 1、Random类 Public Random rd new Random(); int Num_Int rd.Next(1, 100);2、数组上下限。 //定义数组 int[] G_Array new int[1,2,3,4];//一维数组 int[,] G_Array_T …...
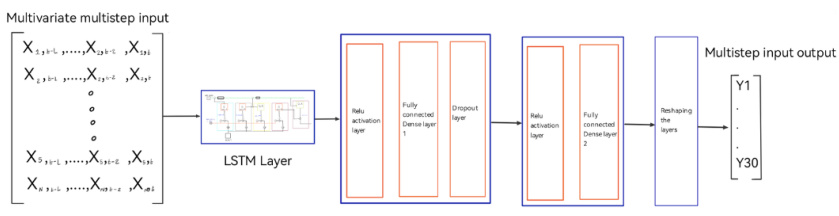
光伏功率预测 | LSTM多变量单步光伏功率预测(Matlab完整源码和数据)
光伏功率预测 | MATLAB实现基于LSTM长短期记忆神经网络的光伏功率预测 目录 光伏功率预测 | MATLAB实现基于LSTM长短期记忆神经网络的光伏功率预测效果一览基本介绍程序设计参考资料 效果一览 基本介绍 光伏功率预测 | LSTM多变量单步光伏功率预测(Matlab完整源码和…...

解锁 AI 大语言模型的“知识宝藏”:知识库的奥秘与优化之道
1. 知识库在 AI 大语言模型中的作用 1.1 提供准确信息 知识库是 AI 大语言模型的重要组成部分,能够为模型提供准确的信息。在处理用户问题时,模型可以参考知识库中的数据,从而给出更准确的答案。例如,在医疗领域,知识…...

一步一步配置 Ubuntu Server 的 NodeJS 服务器详细实录——3. 服务器软件更新,以及常用软件安装
前言 前面,我们已经 安装好了 Ubuntu 服务器系统,并且 配置好了 ssh 免密登录服务器 ,现在,我们要来进一步的设置服务器。 那么,本文,就是进行服务器的系统更新,以及常用软件的安装 调整 Ubu…...

第四十天打卡
知识点回顾: 彩色和灰度图片测试和训练的规范写法:封装在函数中展平操作:除第一个维度batchsize外全部展平dropout操作:训练阶段随机丢弃神经元,测试阶段eval模式关闭dropout 作业:仔细学习下测试和训练代码…...

【请关注】ELK集群部署真实案例分享
ELK集群部署 1,准备es配置 es.yml: -------------------------------------------------------------- #集群名称 cluster.name: elasticsearch-cluster #节点名称 node.name: es-node1 #设置绑定的ip地址,可以使ipv4或者ipv6 #绑定这台机器的任何一个ip network.bind_hos…...

odoo17 windows server布署错误分析
odoo17 windows server布署错误分析 错误代码: File "C:\od172406\odoo\sql_db.py", line 681, in borrow result psycopg2.connect( ^^^^^^^^^^^^^^^^^ File "C:\od172406\venv\Lib\site-packages\psycopg2\__init__.py"…...

PyTorch 入门学习笔记
一、简介 PyTorch 是由 Meta(原 Facebook) 开源的深度学习框架。其前身 Torch 是一个基于 LuaJIT 的科学计算框架,核心功能是提供高效的张量(Tensor)操作和神经网络支持。由于 Lua 语言的生态限制,Torch 逐…...

【 Samba】Windows 用户访问Docker服务器上当前A用户的 ~/aaa目录
要让 Windows 用户访问 ~/aaa目录,需要在 Linux 系统上配置 Samba 共享服务,并设置合适的权限。以下是具体步骤: 1. 安装 Samba bash sudo apt update sudo apt install samba 2. 创建 Samba 用户(可选) 如果你希望 …...

pycharm生成图片
文章目录 图片例子生成图片并储存,设置中文字体支持两条线绘制散点图和直方图绘制条形图(bar)绘制条形图(横着的)(plt.barh)分组的条形图 颜色和线条风格1. **颜色字符 (color)**其他颜色指定方…...
