从0开始学习R语言--Day14--贝叶斯统计与结构方程模型
贝叶斯统计
在很多时候,我们经常会看到在统计分析中出现很多反直觉的结论,比如假如有一种病,人群中的患病率为1%,患者真患病时,检测结果为阳性的概率是99%,如果没有,则检测结果为阳性的概率是5%,但是如果让我们计算一个人检测结果为阳性时真正患病的概率为多少,根据概率公式P(患病|检测为阳性) = [P(检测为阳性|患病)× P(患病)]/P(检测为阳性) 我们可以计算,而P(检测为阳性)可以通过全概率公式P(检测为阳性)=P(检测为阳性|患病)P(患病) + P(检测为阳性|没患病)P(没患病)得出,计算得到的结果为16.67%,可能有人会疑惑,为什么患真病的前提下,检测为阳性时99%,反过来就只有16.67%,其实会有这样的错句,一是因为没抓住基础的概率,即本身该病的患病率就是很低的1%,二是在人群中没病但检测为阳性的人(5%×99%≈4.95%)比有病且检测为阳性的人(1%×99%≈0.99%)多很多。
这种先有对数据样本的初始判断,观察数据在给定假设下的表现,通过后续检验后得出新判断的过程,就是贝叶斯统计,其中,初始的判断叫做先验概率(Prior),即人群中的患病率1%;在某个假设成立的情况下,观察到的表现叫做似然值(Likehood),即患者有病时检测为阳性的概率和没病时检测为阳性的概率,这里是否有病就是假设;在看到计算结果后得出的新判断叫做后验概率(Posterior)。
下面我们依然是给出一个例子来解释:
# 加载必要的库
library(tidyverse)
library(ggplot2)# 定义参数
p_disease <- 0.01 # 患病先验概率(1%)
p_true_positive <- 0.99 # 真阳性率(99%)
p_false_positive <- 0.05 # 假阳性率(5%)# 计算检测为阳性的总概率
p_positive <- (p_true_positive * p_disease) + (p_false_positive * (1 - p_disease))# 计算后验概率(贝叶斯定理)
p_disease_given_positive <- (p_true_positive * p_disease) / p_positive# 打印结果
cat(sprintf("检测为阳性时实际患病的概率: %.2f%%", p_disease_given_positive * 100))# 可视化先验、似然和后验
results <- data.frame(Scenario = c("Prior", "Likelihood (Disease)", "Likelihood (No Disease)", "Posterior"),Probability = c(p_disease, p_true_positive, p_false_positive, p_disease_given_positive)
)ggplot(results, aes(x = Scenario, y = Probability, fill = Scenario)) +geom_bar(stat = "identity") +geom_text(aes(label = scales::percent(Probability)), vjust = -0.5) +scale_y_continuous(labels = scales::percent) +labs(title = "贝叶斯分析: 疾病检测案例",subtitle = "先验、似然和后验概率比较",y = "概率") +theme_minimal()# 更详细的模拟分析
set.seed(123)
population_size <- 10000# 生成模拟人群
sim_data <- data.frame(id = 1:population_size,disease = rbinom(population_size, 1, p_disease),test_result = NA
)# 模拟检测结果
sim_data <- sim_data %>%mutate(test_result = case_when(disease == 1 ~ rbinom(n(), 1, p_true_positive),disease == 0 ~ rbinom(n(), 1, p_false_positive)))# 计算实际阳性中患病的比例
empirical_posterior <- sim_data %>%filter(test_result == 1) %>%summarise(p_disease_given_positive = mean(disease)) %>%pull()cat(sprintf("\n模拟数据中阳性结果实际患病的比例: %.2f%%", empirical_posterior * 100))# 创建列联表展示结果
table(sim_data$disease, sim_data$test_result) %>%addmargins() %>%knitr::kable(caption = "疾病与检测结果的列联表")输出:
检测为阳性时实际患病的概率: 16.67%>
模拟数据中阳性结果实际患病的比例: 17.09%>
Table: 疾病与检测结果的列联表| | 0| 1| Sum|
|:---|----:|---:|-----:|
|0 | 9414| 485| 9899|
|1 | 1| 100| 101|
|Sum | 9415| 585| 10000|
从输出中我们可以看到,模拟数据中的实际患病率与我们用贝叶斯统计计算得出的差不多,而输出的列表里也能观察到阳性预测的正确率只有100/585≈17.09%,这说明在实际上的应用场景中,我们在看到类似于“99%的准确率”时不要被误导,要验证过基础概率后再下结论,相对的,假如在信用评分模型中,用户的违约率很低,那么如果出现很多高风险决策,这也可能是误报,当然最好是要查看背后的解释。
结构方程模型
事实上,并不是所有的数据都会跟我们平常做练习和书上的一样是每个都很好理解的,很多时候我们想研究的变量,是分散在不同的数据上的,这个时候探讨出变量间的关系,就需要我们潜在的变量了,是这些变量在无形之中担当了变量之间的桥梁。
例如我们知道不同的老师对学生成绩有不同的影响,也许我们会去分析不同的教学方法是怎么影响成绩的,但如果直接对这两者做回归分析,很多时候效果都会很差,究其原因是因为教学方法很可能是间接影响了B,再由B去影响学生成绩,所以这里的重点工作就变成了如何找出B。当然,这种潜在变量并不是唯一的,需要我们提出假设去验证。
但往往潜在变量都是抽象的(毕竟明显的变量在拿到数据的时候,就会看出来),这个时候就需要我们自己人为设计一些测量的工具来代替潜在变量的影响,假设我们认为潜在变量是教学质量,那么我们就可以从教师评分,课程设计、作业反馈上得出来(前提是控制同一批能力差不多的学生),通过设计问题和学生对知识掌握过程中的进步,我们可以得出该教师方法的质量处于什么水平;亦或者认为潜在变量是学生的学习动机,那么可能就需要用学生平时的学习时间,在课堂上的互动程度,对自我的评价,通过学生对学习的感兴趣程度和是否积极的态度来判断。
依然是举一个例子来说明:
library(lavaan) # 结构方程建模
library(tidySEM) # 可视化
library(ggplot2) # 基础绘图
library(dplyr)set.seed(123)
n_students <- 300# 生成潜变量(不可直接观测的真实值)
true_motivation <- rnorm(n_students, mean = 0, sd = 1)
true_teaching <- rnorm(n_students, mean = 0, sd = 1)# 生成观测指标(带测量误差)
student_data <- data.frame(# 学习动机的观测指标study_time = round(2 + 0.5*true_motivation + rnorm(n_students, 0, 0.3), 1),participation = round(3 + 0.7*true_motivation + rnorm(n_students, 0, 1)),self_eval = round(5 + 0.6*true_motivation + rnorm(n_students, 0, 1)),# 教学质量的观测指标teach_rating = round(6 + 0.8*true_teaching + rnorm(n_students, 0, 1)),course_diff = round(4 - 0.5*true_teaching + rnorm(n_students, 0, 1)), # 难度与质量负相关hw_feedback = round(5 + 0.7*true_teaching + rnorm(n_students, 0, 1)),# 成绩变量(受潜变量影响)math_score = round(75 + 5*true_motivation + 3*true_teaching + rnorm(n_students, 0, 5)),chinese_score = round(78 + 6*true_motivation + rnorm(n_students, 0, 4))
)model <- '# 测量模型 (Latent Variable Definitions)motivation =~ 1*study_time + participation + self_eval # 固定第一个载荷为1teaching_quality =~ 1*teach_rating + course_diff + hw_feedback# 结构模型 (Regressions)math_score ~ motivation + teaching_qualitychinese_score ~ motivation# 潜变量间关系motivation ~ teaching_quality# 残差相关(可选)# study_time ~~ participation
'fit <- sem(model, data = student_data,estimator = "MLR") # 使用稳健最大似然估计summary(fit, standardized = TRUE, fit.measures = TRUE)# 路径图
graph_sem(fit, layout = get_layout("teaching_quality", "motivation","math_score", "chinese_score",rows = 2),edge.label.cex = 0.9,sizeMan = 6, sizeLat = 8,curvature = 60)# 因子载荷可视化(ggplot2版)
parameterEstimates(fit, standardized = TRUE) %>%filter(op == "=~") %>%ggplot(aes(x = rhs, y = std.all, fill = lhs)) +geom_col(position = "dodge") +geom_hline(yintercept = 0.5, linetype = "dashed", color = "red") +labs(title = "标准化因子载荷",y = "标准化系数", x = "观测指标") +coord_flip() +theme_minimal()输出:
lavaan 0.6-19 ended normally after 77 iterationsEstimator MLOptimization method NLMINBNumber of model parameters 19Number of observations 300Model Test User Model:Standard ScaledTest Statistic 20.142 20.875Degrees of freedom 17 17P-value (Chi-square) 0.267 0.232Scaling correction factor 0.965Yuan-Bentler correction (Mplus variant) Model Test Baseline Model:Test statistic 544.259 551.226Degrees of freedom 28 28P-value 0.000 0.000Scaling correction factor 0.987User Model versus Baseline Model:Comparative Fit Index (CFI) 0.994 0.993Tucker-Lewis Index (TLI) 0.990 0.988Robust Comparative Fit Index (CFI) 0.993Robust Tucker-Lewis Index (TLI) 0.988Loglikelihood and Information Criteria:Loglikelihood user model (H0) -4424.677 -4424.677Scaling correction factor 1.023for the MLR correction Loglikelihood unrestricted model (H1) -4414.606 -4414.606Scaling correction factor 0.995for the MLR correction Akaike (AIC) 8887.354 8887.354Bayesian (BIC) 8957.726 8957.726Sample-size adjusted Bayesian (SABIC) 8897.470 8897.470Root Mean Square Error of Approximation:RMSEA 0.025 0.02890 Percent confidence interval - lower 0.000 0.00090 Percent confidence interval - upper 0.060 0.063P-value H_0: RMSEA <= 0.050 0.857 0.828P-value H_0: RMSEA >= 0.080 0.002 0.004Robust RMSEA 0.02790 Percent confidence interval - lower 0.00090 Percent confidence interval - upper 0.061P-value H_0: Robust RMSEA <= 0.050 0.845P-value H_0: Robust RMSEA >= 0.080 0.003Standardized Root Mean Square Residual:SRMR 0.038 0.038Parameter Estimates:Standard errors SandwichInformation bread ObservedObserved information based on HessianLatent Variables:Estimate Std.Err z-value P(>|z|) Std.lv Std.allmotivation =~ study_time 1.000 0.473 0.859participation 1.435 0.159 9.022 0.000 0.679 0.547self_eval 1.013 0.159 6.355 0.000 0.480 0.435teaching_quality =~ teach_rating 1.000 0.812 0.618course_diff -0.680 0.135 -5.046 0.000 -0.552 -0.473hw_feedback 0.840 0.174 4.838 0.000 0.683 0.580Regressions:Estimate Std.Err z-value P(>|z|) Std.lv Std.allmath_score ~ motivation 9.753 1.191 8.190 0.000 4.616 0.623teaching_qulty 3.792 0.726 5.224 0.000 3.080 0.415chinese_score ~ motivation 11.243 1.080 10.411 0.000 5.322 0.750motivation ~ teaching_qulty -0.073 0.055 -1.333 0.183 -0.125 -0.125Covariances:Estimate Std.Err z-value P(>|z|) Std.lv Std.all.math_score ~~ .chinese_score 3.446 2.361 1.460 0.144 3.446 0.139Variances:Estimate Std.Err z-value P(>|z|) Std.lv Std.all.study_time 0.079 0.017 4.801 0.000 0.079 0.262.participation 1.079 0.099 10.941 0.000 1.079 0.701.self_eval 0.986 0.085 11.611 0.000 0.986 0.811.teach_rating 1.070 0.146 7.344 0.000 1.070 0.619.course_diff 1.062 0.098 10.879 0.000 1.062 0.777.hw_feedback 0.918 0.111 8.297 0.000 0.918 0.663.math_score 27.738 3.708 7.480 0.000 27.738 0.504.chinese_score 22.022 2.557 8.613 0.000 22.022 0.437.motivation 0.221 0.028 7.806 0.000 0.984 0.984teaching_qulty 0.660 0.168 3.935 0.000 1.000 1.000

从输出中我们可以看到,CFI,RMSEA等指标都在标准范围内,说明模型与数据的匹配性较高;观察学习动机和教学质量中的指标,可以发现学习时间最能反映学习动机,而自我评价对模型的影响则较小;观察教学质量中的指标,可以发现课程难度与教学质量是负相关的,这也在我们的预期之内,毕竟越难的课,学生听懂的难度也会加大,而不是好的老师就能一下子把学生教会。综合来看,学习动机对语文和数学的成绩都较大,而教学质量会直接影响数学成绩,而对学习动机的影响反倒不大((β=-0.125, p=0.183))。
相关文章:

从0开始学习R语言--Day14--贝叶斯统计与结构方程模型
贝叶斯统计 在很多时候,我们经常会看到在统计分析中出现很多反直觉的结论,比如假如有一种病,人群中的患病率为1%,患者真患病时,检测结果为阳性的概率是99%,如果没有,则检测结果为阳性的概率是5…...

02-BTC-密码学原理 对hash算法如果出现漏洞的思考
如果比特币中某个哈希函数的抗碰撞性出现了漏洞怎么办,怎么补救? 答:(1)攻击场景: 伪造交易:攻击者可构造两个不同的交易(如正常交易和恶意双花交易)具有相同的TxID&…...

[Python] 如何使用 Python 调用 Dify 工作流服务实现自动化翻译
在实际项目中,自动化工作流服务可以大大简化复杂任务的处理流程。本文将介绍如何通过 Python 脚本调用 Dify 提供的工作流 API,实现文本翻译的自动化操作。该流程包括设置 API 接口、构造请求体并处理返回结果。 一、背景介绍:什么是 Dify 工作流服务? Dify 是一款支持多种…...

分布式微服务系统架构第142集:全栈开发
加群联系作者vx:xiaoda0423 仓库地址:https://webvueblog.github.io/JavaPlusDoc/ https://1024bat.cn/ https://github.com/webVueBlog/fastapi_plus https://webvueblog.github.io/JavaPlusDoc/ /*** 本地启动解决跨域问题* 打包发布请注释该类&#…...

PTA-根据已有类Worker,使用LinkedList编写一个WorkerList类,实现计算所有工人总工资的功能。
目录 1.问题描述 2.函数接口定义: 3.裁判测试程序样例: 4.输入和输出样例 输入样例: 输出样例: 5.实现代码 1.问题描述 Main类:在main方法中,调用constructWorkerList方法构建一个Worker对象链表…...

文档整合自动化
主要功能是按照JSON文件(Sort.json)中指定的顺序合并多个Word文档(.docx),并清除文档中的所有超链接。最终输出合并后的文档名为"sorted_按章节顺序.docx"。 主要分为几个部分: 初始化配置 定…...

微软markitdown PDF/WORD/HTML文档转Markdown格式软件整合包下载
本次和大家分享另一个微软发布的非常热门的文件文档转Markdown格式文档的软件markitdown,软件可以将PDF,word,ppt,Excel等十几种格式文档转换为markdown格式文档,我基于当前最新0.1.2版本制作了免安装一键启动整合包。…...

科普:Linux `su` 切换用户后出现 `$` 提示符,如何排查和解决?
科普:Linux su 切换用户后出现 $ 提示符,如何排查和解决? 在 Linux 系统管理中,su(Switch User)命令用于切换用户身份。正常情况下,从 root 切换到普通用户时,提示符会从 # 变成 $&…...

BayesFlow:基于神经网络的摊销贝叶斯推断框架
贝叶斯推断为不确定性条件下的推理、复杂系统建模以及基于观测数据的预测提供了严谨且功能强大的理论框架。尽管贝叶斯建模在理论上具有优雅性,但在实际应用中经常面临显著的计算挑战:后验分布通常缺乏解析解,模型验证和比较需要进行重复的推…...
)
NodeJS全栈开发面试题讲解——P9性能优化(Node.js 高级)
✅ 9.1 Node.js 的性能瓶颈一般出在哪?如何排查? Node.js 单线程 异步模型,瓶颈常出现在: 阻塞操作(如:同步 I/O、CPU 密集型计算) 数据库慢查询 / 索引失效 外部接口慢响应 大量并发请求导…...

NVMe IP现状扫盲
SSD优势 与机械硬盘(Hard Disk Driver, HDD)相比,基于Flash的SSD具有更快的数据随机访问速度、更快的传输速率和更低的功耗优势,已经被广泛应用于各种计算领域和存储系统。SSD最初遵循为HDD设计的现有主机接口协议,例…...

5G-A时代与p2p
5G-A时代正在走来,那么对P2P的影响有多大。 5G-A作为5G向6G过渡的关键技术,将数据下载速率从千兆提升至万兆,上行速率从百兆提升至千兆,时延降至毫秒级。这种网络性能的跨越式提升,为P2P提供了更强大的底层支撑&#x…...
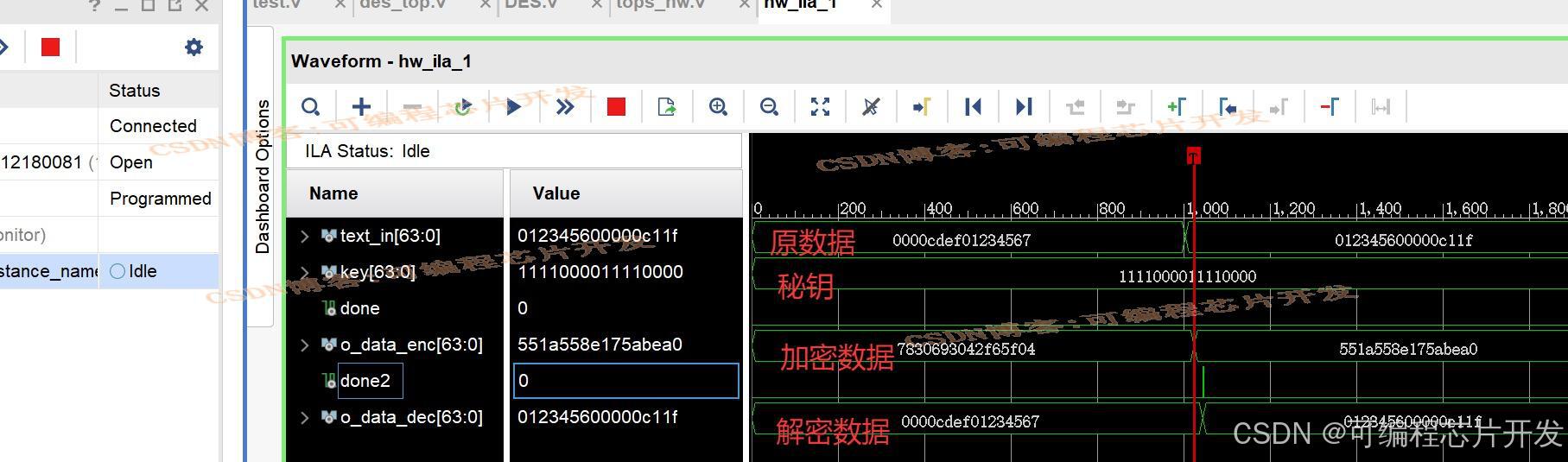
基于FPGA的DES加解密系统verilog实现,包含testbench和开发板硬件测试
目录 1.课题概述 2.系统测试效果 3.核心程序与模型 4.系统原理简介 5.完整工程文件 1.课题概述 基于FPGA的DES加解密系统verilog实现,包含testbench和开发板硬件测试。输入待加密数据,密钥,输出加密数据,然后通过解密模块输出解密后的原…...
)
基于生产-消费模式,使用Channel进行文件传输(Tcp方式)
Client端: #region 多文件传输 public class FileMetadata {public string FileName { get; set; }public long FileSize { get; set; } }class Program {const int PORT 8888;const int BUFFER_SIZE 60 * 1024 * 1024;//15s-50 25s-64 33s-32 27s-50 31s-40 25…...

tortoisegit 使用rebase修改历史提交
在 TortoiseGit 中使用 rebase 修改历史提交(如修改提交信息、合并提交或删除提交)的步骤如下: --- ### **一、修改最近一次提交** 1. **操作**: - 右键项目 → **TortoiseGit** → **提交(C)** - 勾选 **"Amend…...

Python----目标检测(《用于精确目标检测和语义分割的丰富特征层次结构》和R-CNN)
一、《用于精确目标检测和语义分割的丰富特征层次结构》 1.1、基本信息 原文标题:Rich feature hierarchies for accurate object detection and semantic segmentation 中文译名:用于精确目标检测与语义分割的丰富特征层次结构 版本:第5版技…...

Ansible 进阶 - Roles 与 Inventory 的高效组织
Ansible 进阶 - Roles 与 Inventory 的高效组织 如果说 Playbook 是一份完整的“菜谱”,那么 Role (角色) 就可以被看作是制作这道菜(或一桌菜)所需的标准化“备料包”或“半成品组件”。例如,我们可以有一个“Nginx Web 服务器安装配置 Role”、“MySQL 数据库基础设置 Ro…...

极简以太彩光网络解决方案4.0正式发布,“彩光”重构园区网络极简之道
5月28日下午,锐捷网络在京举办以“光,本该如此‘简单’”为主题的发布会,正式发布极简以太彩光网络解决方案4.0。作为“彩光”方案的全新进化版本,极简以太彩光4.0从用户需求出发,聚焦场景洞察,开启了一场从底层基因出发的极简革命,通过架构、部署、运维等多维度的创新升级,以强…...

国芯思辰| 霍尔电流传感器AH811为蓄电池负载检测系统安全护航
在电动车、储能电站、不间断电源(UPS)等设备中,蓄电池作为关键的储能单元,其运行状态直接关系到设备的稳定性和使用寿命。而准确监测蓄电池的负载情况,是保障其安全、高效运行的关键。霍尔电流传感器 AH811凭借独特的技…...

TortoiseSVN账号切换
SVN登录配置及账号切换 本文主要为了解答svn客户端如何进行账号登录及切换不同权限账号的方式。 一、环境准备与客户端安装 安装TortoiseSVN客户端 下载地址:TortoiseSVN官网 安装步骤: 双击安装包,按向导完成安装后&#x…...

2025年05月28日Github流行趋势
项目名称:agenticSeek 项目地址url:https://github.com/Fosowl/agenticSeek项目语言:Python历史star数:10352今日star数:2444项目维护者:Fosowl, steveh8758, klimentij, ganeshnikhil, apps/copilot-pull-…...
:商业模式与阶段匹配的指标体系构建)
精益数据分析(91/126):商业模式与阶段匹配的指标体系构建
精益数据分析(91/126):商业模式与阶段匹配的指标体系构建 在创业的不同阶段,企业面临的核心问题与目标差异显著,这就要求我们依据商业模式和所处阶段,动态调整关键指标体系。今天,我们将深入解…...

篇章五 数据结构——链表(一)
目录 1.ArrayList的缺陷 2. 链表 2.1 链表的概念及结构 2.2 链表结构 1. 单向或者双向 2.带头或者不带头 3.循环或者非循环 2.3 链表的实现 1.完整代码 2.图解 3.显示方法 4.链表大小 5. 链表是否存在 key 值 6.头插法 7.尾插法 8.中间插入 9.删除key值节点 10.…...
一文清晰理解目标检测指标计算
一、核心概念 1.交并比IoU 预测边界框与真实边界框区域的重叠比,取值范围为[0,1] 设预测边界框为,真实边界框为 公式: IoU计算为两个边界框交集面积与并集面积之比,图示如下 IoU值越高,表示预测边界框与真实边界框的对…...

【MySQL】索引下推减少回表次数
一、简述索引下推 “索引下推”是数据库领域的一个术语,主要出现在MySQL(尤其是InnoDB存储引擎)中,英文名叫 Index Condition Pushdown,简称 ICP。就是过滤的动作由下层的存储引擎层通过使用索引来完成,而…...

Artificial Analysis2025年Q1人工智能发展六大趋势总结
2025年第一季度人工智能发展六大趋势总结 ——基于《Artificial Analysis 2025年Q1人工智能报告》 趋势一:AI持续进步,竞争格局白热化 前沿模型竞争加剧:OpenAI凭借“o4-mini(高智能版)”保持领先,但谷歌&…...

DeepSeek模型高级应用:提示工程与Few-shot学习实战指南
引言 在DeepSeek模型的实际应用中,提示工程(Prompt Engineering)和Few-shot学习正成为提升模型性能的关键技术。相比全参数微调,这些技术能以更低成本实现领域适配。本文将深入解析DeepSeek模型的高级提示技巧、动态Few-shot实现方案,以及混合微调策略,帮助开发者在资源受…...

Android高级开发第三篇 - JNI异常处理与线程安全编程
Android高级开发第三篇 - JNI异常处理与线程安全编程 Android高级开发第三篇 - JNI异常处理与线程安全编程引言为什么要关注异常处理和线程安全?第一部分:JNI异常处理基础什么是JNI异常?检查和处理Java异常从C代码抛出Java异常异常处理的最佳…...

企业级应用狂潮:从Spotify到LinkedIn的Llama实战手册
当Spotify用Llama生成的个性化推荐文案让用户播放时长激增30%, 当LinkedIn靠开源框架将社交推荐延迟降低40%—— 企业级AI战场正经历从“技术炫技”到“利润引擎”的残酷蜕变。 核心数据:企业采用率爆发式增长(2025 Gartner调研) 指标2023年2025年增幅开源模型采用率42%87%…...

高效管理 Python 项目的 UV 工具指南
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 持续学习,不断…...
