二维 根据矩阵变换计算缩放比例
在二维空间中,根据矩阵变换计算缩放比例是一个常见的图形学问题。通常,我们通过分析变换矩阵的结构来提取出缩放(Scale)信息。以下是详细的分析和计算方法。
🧮 一、基础:二维变换矩阵结构
在二维仿射变换中,常用的变换矩阵形式为 3x3 的齐次坐标矩阵,如下所示:
[ a b t x c d t y 0 0 1 ] \begin{bmatrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{bmatrix} ac0bd0txty1
其中:
- $ a, b, c, d $:描述线性变换(如缩放、旋转、剪切)
- $ t_x, t_y $:表示平移
- 最后一行
[0, 0, 1]是齐次坐标标准形式的一部分
📐 二、纯缩放矩阵
如果变换矩阵仅包含缩放(无旋转、剪切、平移),则其形式为:
[ S x 0 0 0 S y 0 0 0 1 ] \begin{bmatrix} S_x & 0 & 0 \\ 0 & S_y & 0 \\ 0 & 0 & 1 \end{bmatrix} Sx000Sy0001
此时,缩放比例直接为:
- $ S_x $:x轴缩放比例
- $ S_y $:y轴缩放比例
🧩 三、包含旋转的变换矩阵
如果变换矩阵包含旋转(Rotation)和缩放(Scale),则矩阵形式为:
[ S x ⋅ cos θ − S y ⋅ sin θ t x S x ⋅ sin θ S y ⋅ cos θ t y 0 0 1 ] \begin{bmatrix} S_x \cdot \cos\theta & -S_y \cdot \sin\theta & t_x \\ S_x \cdot \sin\theta & S_y \cdot \cos\theta & t_y \\ 0 & 0 & 1 \end{bmatrix} Sx⋅cosθSx⋅sinθ0−Sy⋅sinθSy⋅cosθ0txty1
此时,缩放比例不能直接从 $ a, d $ 提取,而是通过以下方法计算:
✅ 方法一:计算基向量的长度
-
x轴方向:取矩阵第一列(忽略平移)向量 $ \vec{v}_x = \begin{bmatrix} a \ c \end{bmatrix} $
S x = ∥ v ⃗ x ∥ = a 2 + c 2 S_x = \|\vec{v}_x\| = \sqrt{a^2 + c^2} Sx=∥vx∥=a2+c2 -
y轴方向:取矩阵第二列(忽略平移)向量 $ \vec{v}_y = \begin{bmatrix} b \ d \end{bmatrix} $
S y = ∥ v ⃗ y ∥ = b 2 + d 2 S_y = \|\vec{v}_y\| = \sqrt{b^2 + d^2} Sy=∥vy∥=b2+d2
✅ 该方法适用于矩阵中没有剪切(Shear)成分的情况。
📌 四、包含剪切(Shear)的变换矩阵
如果变换矩阵中包含剪切(Shear)成分,那么缩放和剪切信息会相互影响,此时需要使用矩阵分解技术,如:
- 奇异值分解(SVD)
- 极分解(Polar Decomposition)
这些方法较为复杂,通常用于高级图形学或物理模拟中,超出基础缩放提取的范畴。
📈 五、示例:从变换矩阵中提取缩放比例
假设我们有如下变换矩阵(包含旋转和缩放):
[ 3 − 4 0 4 3 0 0 0 1 ] \begin{bmatrix} 3 & -4 & 0 \\ 4 & 3 & 0 \\ 0 & 0 & 1 \end{bmatrix} 340−430001
- 第一列:$ \vec{v}_x = \begin{bmatrix} 3 \ 4 \end{bmatrix} $
- 第二列:$ \vec{v}_y = \begin{bmatrix} -4 \ 3 \end{bmatrix} $
计算缩放比例:
S x = 3 2 + 4 2 = 5 S y = ( − 4 ) 2 + 3 2 = 5 S_x = \sqrt{3^2 + 4^2} = 5 \\ S_y = \sqrt{(-4)^2 + 3^2} = 5 Sx=32+42=5Sy=(−4)2+32=5
因此,该矩阵在 x 和 y 方向都进行了 5 倍的缩放。
⚠️ 六、注意事项
| 项目 | 说明 |
|---|---|
| 矩阵方向 | 确保矩阵是列优先(Column-Major)还是行优先(Row-Major),影响向量提取 |
| 剪切影响 | 若矩阵中包含剪切,直接提取缩放比例将不准确 |
| 齐次坐标 | 平移部分不影响缩放,可忽略 |
| 数值精度 | 实际应用中,注意浮点数误差对计算结果的影响 |
✅ 七、总结:如何计算二维变换矩阵的缩放比例
| 情况 | 方法 |
|---|---|
| 纯缩放矩阵 | 直接读取对角线元素 $ S_x = a, S_y = d $ |
| 包含旋转的矩阵 | 计算第一列和第二列向量的长度:$ S_x = |\vec{v}_x|, S_y = |\vec{v}_y| $ |
| 包含剪切的矩阵 | 使用 SVD 或极分解等高级方法 |
| 实际开发中 | 可使用图形库(如 Unity、OpenGL、DirectX)提供的矩阵分解函数 |
相关文章:

二维 根据矩阵变换计算缩放比例
在二维空间中,根据矩阵变换计算缩放比例是一个常见的图形学问题。通常,我们通过分析变换矩阵的结构来提取出缩放(Scale)信息。以下是详细的分析和计算方法。 🧮 一、基础:二维变换矩阵结构 在二维仿射变换…...

Vue-Cropper:全面掌握图片裁剪组件
Vue-Cropper 完全学习指南:Vue图片裁剪组件 🎯 什么是 Vue-Cropper? Vue-Cropper 是一个简单易用的Vue图片裁剪组件,支持Vue2和Vue3。它提供了丰富的配置选项和回调方法,可以满足各种图片裁剪需求。 🌟 …...

建造者模式:优雅构建复杂对象
引言 在软件开发中,有时我们需要创建一个由多个部分组成的复杂对象,这些部分可能有不同的变体或配置。如果直接在一个构造函数中设置所有参数,代码会变得难以阅读和维护。当对象构建过程复杂,且需要多个步骤时,我们可…...

现场总线结构在楼宇自控系统中的技术要求与实施要点分析
在建筑智能化程度不断提升的当下,楼宇自控系统承担着协调建筑内各类设备高效运行的重任。传统的集中式控制系统在面对复杂建筑环境时,逐渐暴露出布线繁琐、扩展性差、可靠性低等问题。而现场总线结构凭借其分散控制、通信高效等特性,成为楼宇…...
)
Axure组件即拖即用:垂直折叠菜单(动态展开/收回交互)
亲爱的小伙伴,在您浏览之前,请关注一下,在此深表感谢!如有帮助请订阅专栏!免费哦! 你是不是也这样崩溃过? 明明设置了点击交互,菜单却像死机一样纹丝不动,F5按烂了都没反…...
学习路之PHP--easyswoole使用视图和模板
学习路之PHP--easyswoole使用视图和模板 一、安装依赖插件二、 实现渲染引擎三、注册渲染引擎四、测试调用写的模板五、优化六、最后补充 一、安装依赖插件 composer require easyswoole/template:1.1.* composer require topthink/think-template相关版本: "…...

《云原生安全攻防》-- K8s网络策略:通过NetworkPolicy实现微隔离
默认情况下,K8s集群的网络是没有任何限制的,所有的Pod之间都可以相互访问。这就意味着,一旦攻击者入侵了某个Pod,就能够访问到集群中任意Pod,存在比较大的安全风险。 在本节课程中,我们将详细介绍如何通过N…...

06 APP 自动化- H5 元素定位
文章目录 H5 元素定位1、APP 分类2、H5 元素3、H5 元素定位环境的搭建4、代码实现: H5 元素定位 1、APP 分类 1、Android 原生 APP2、混合 APP(Android 原生控件H5页面)3、纯 H5 App 2、H5 元素 H5 元素容器 WebViewWebView 控件实现展示网页 3、H5 元素定位环…...
)
Axure疑难杂症:中继器新增数据时如何上传并存储图片(玩转中继器)
亲爱的小伙伴,在您浏览之前,烦请关注一下,在此深表感谢!如有帮助请订阅专栏! Axure产品经理精品视频课已登录CSDN可点击学习https://edu.csdn.net/course/detail/40420 案例视频: 中继器新增数据时如何上传并存储图片 课程主题:中继器新增数据时如何上传并存储图片 主…...

定时线程池失效问题引发的思考
最近在做的一个新功能,在结果探测的时候使用了定时线程池和普通线程池结合,定时线程池周期性创建子任务并往普通线程池提交任务。 问题: 在昨天测试老师发现,业务实际上已经成功了,但是页面还是一直显示进行中。 收到…...

Vue-ref 与 props
一、前言 在 Vue 的组件化开发中,父子组件之间的数据传递 是一个非常核心的需求。常见的场景包括: 父组件向子组件传递数据;子组件向父组件发送事件或数据;父组件直接调用子组件的方法或访问其属性。 Vue 提供了多种机制来实现…...

AXURE安装+汉化-Windows
安装网站:https://www.axure.com/release-history/rp9 Axure中文汉化包下载地址 链接:https://pan.baidu.com/s/1U62Azk8lkRPBqWAcrJMFew?pwd5418 提取码:5418 下载完成之后,crtlc lang文件夹 到下载的Axure路径下 双击点进这个目录里面。ctrlv把lan…...

ArcGIS Pro字段计算器与计算几何不可用,显示灰色
“字段计算器”不可用 如果计算字段命令不可用,请考虑以下可能性: 由 ArcGIS 管理的字段无法手动编辑。因此,无法计算 ObjectID(OID 或 FID)字段或地理数据库要素类的 Shape_Length 和 Shape_Area 字段的字段值。表中…...

mac电脑安装 nvm 报错如何解决
前言 已知:安装nvm成功;终端输入nvm -v 有版本返回 1. 启动全局配置环境变量失败 source ~/.zshrc~ 返回: source: no such file or directory: /Users/你的用户名/.zshrc~2 安装node失败 nvm install 16.13返回: mkdir: /U…...
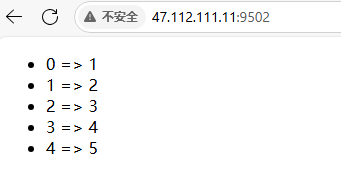
第11节 Node.js 模块系统
为了让Node.js的文件可以相互调用,Node.js提供了一个简单的模块系统。 模块是Node.js 应用程序的基本组成部分,文件和模块是一一对应的。换言之,一个 Node.js 文件就是一个模块,这个文件可能是JavaScript 代码、JSON 或者编译过的…...

上海工作机会:Technical Writer Senior Technical Writer - 中微半导体设备
大名鼎鼎的中微半导体招聘文档工程师了,就是那家由中国半导体产业的领军人物尹志尧领导的、全员持股的公司。如果你还不了解他,赶快Deepseek一下“尹志尧”了解。 招聘职位:Technical Writer & Senior Technical Writer 公司名称&#…...

String 学习总结
1. 存储机制 短字符串优化(SSO, Small String Optimization) 现代标准库中的字符串实现普遍采用 SSO 技术,将长度较短(例如 ≤15 字节)的字符串数据直接存储在字符串对象内部的固定缓冲区(栈上)…...

Python微积分可视化:从导数到积分的交互式教学工具
Python微积分可视化:从导数到积分的交互式教学工具 一、引言 微积分是理解自然科学的基础,但抽象的导数、积分概念常让初学者感到困惑。本文基于Matplotlib开发一套微积分可视化工具,通过动态图像直观展示导数的几何意义、积分的近似计算及跨学科应用,帮助读者建立"数…...

Juce实现Table自定义
Juce实现Table自定义 一.总体展示概及概述 在项目中Juce中TableList往往无法满足用户需求,头部和背景及背景颜色设置以及在Cell中添加自定义按钮,所以需要自己实现自定义TabelList,该示例是展示实现自定义TableList,实现自定义标…...

【25.06】fabric进行caliper测试加环境部署
前置条件 安装一个Ubuntu20+的镜像 基础环境安装 Git cURL vim jq sudo apt install -y git curl vim jq Docker和Docker-compose 这个命令会自动安装docker sudo apt install docker-compose sudo chmod +x /usr/bin/docker-compose docker versiondocker-compose vers…...

【后端高阶面经:架构篇】51、搜索引擎架构与排序算法:面试关键知识点全解析
一、搜索引擎核心基石:倒排索引技术深度解析 (一)倒排索引的本质与构建流程 倒排索引(Inverted Index)是搜索引擎实现快速检索的核心数据结构,与传统数据库的正向索引(文档→关键词࿰…...

Windows应用-音视频捕获
下载“Windows应用-音视频捕获”项目 本应用可以同时捕获4个视频源和4个音频源,可以监视视频源图像,监听音频源;可以将视频源图像写入MP4文件,将音频源写入MP3或WAV文件;还可以录制系统播放的声音。本应用使用MFC对话框…...
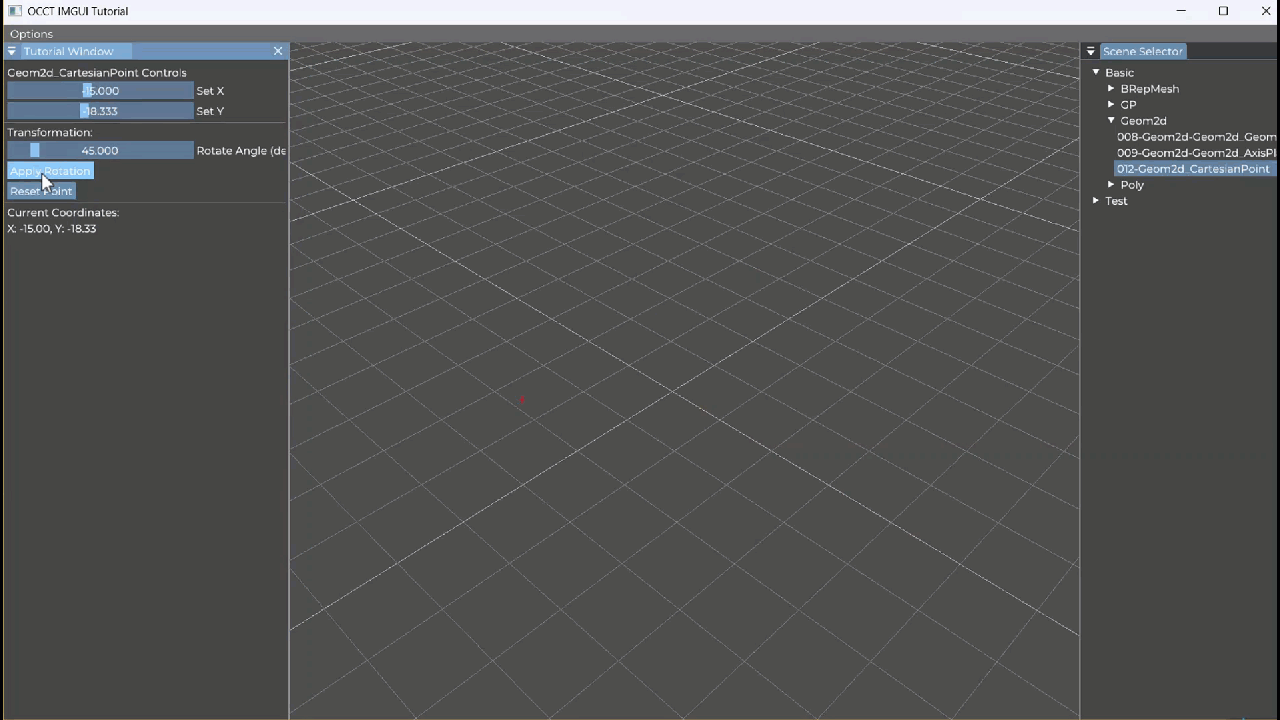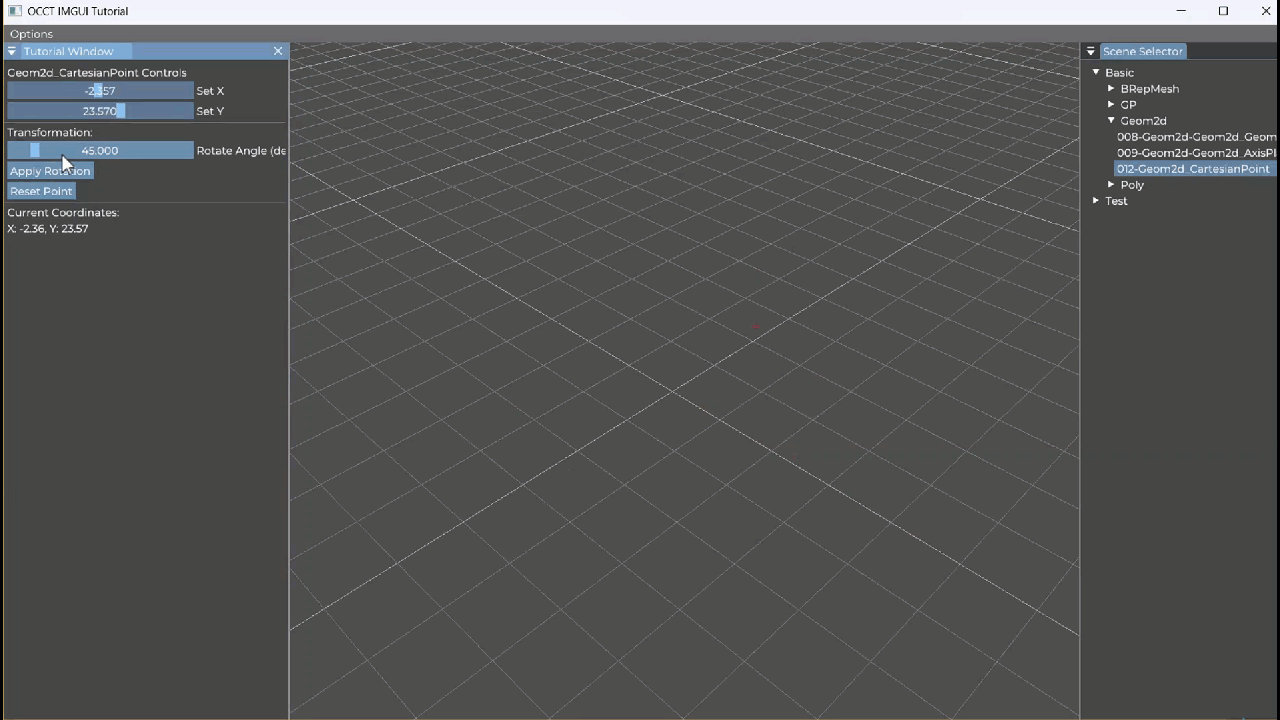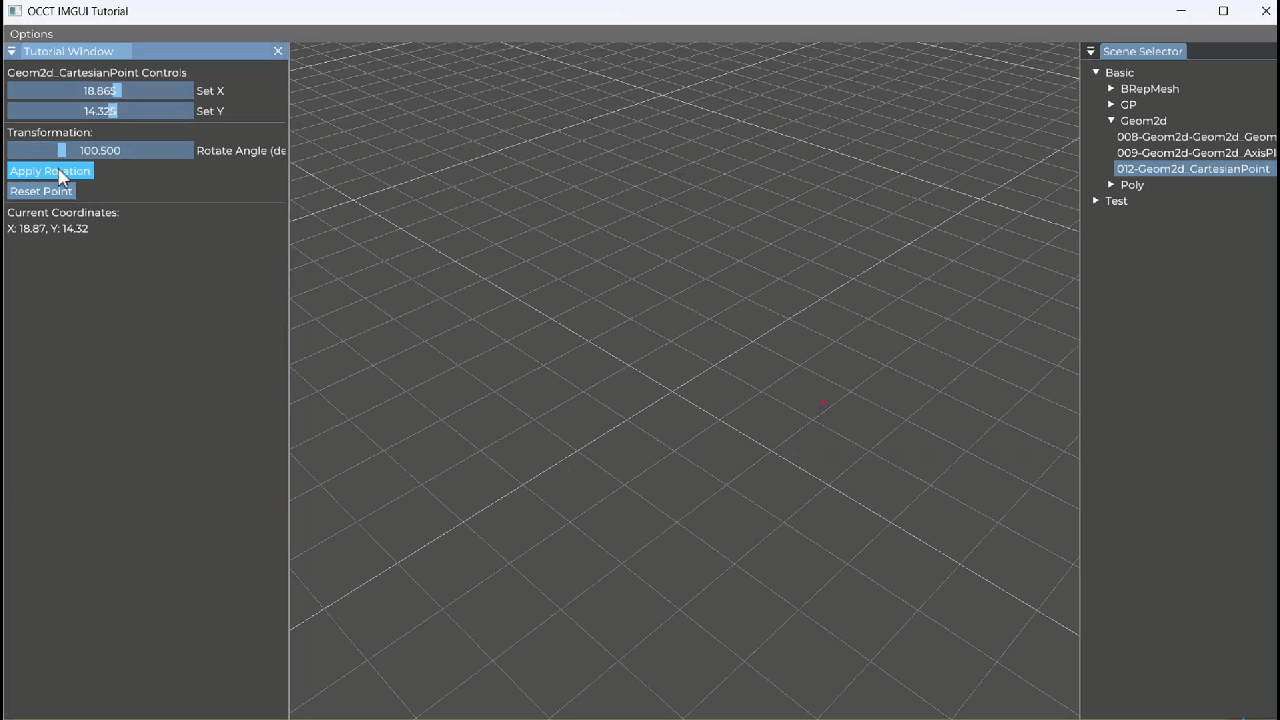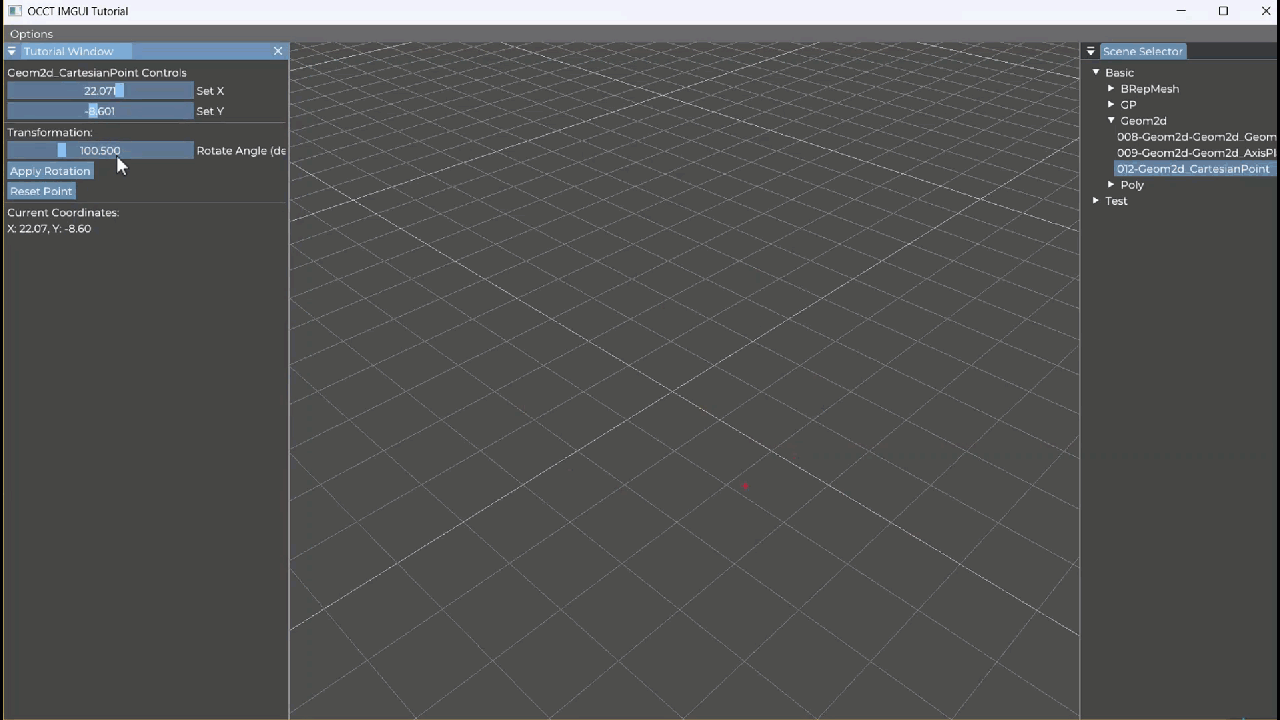
【OCCT+ImGUI系列】012-Geom2d_AxisPlacement
Geom2d_AxisPlacement 教学笔记 一、类概述 Geom2d_AxisPlacement 表示二维几何空间中的一个坐标轴(轴系),由两部分组成: gp_Pnt2d:原点(Location)gp_Dir2d:单位方向向量ÿ…...

优化WP外贸建站提升用户体验
WordPress作为一个强大的建站工具,通过合理的优化,可以提升用户体验,吸引更多潜在客户。本文将为您介绍一些优化WordPress外贸建站的实用建议。 1. 响应式设计 随着移动设备的普及,确保您的WordPress网站具有响应式设计变得至关…...

【C++高并发内存池篇】性能卷王养成记:C++ 定长内存池,让内存分配快到飞起!
📝本篇摘要 在本篇将介绍C定长内存池的概念及实现问题,引入内存池技术,通过实现一个简单的定长内存池部分,体会奥妙所在,进而为之后实现整体的内存池做铺垫! 🏠欢迎拜访🏠ÿ…...

mac下通过anaconda安装Python
本次分享mac下通过anaconda安装Python、Jupyter Notebook、R。 anaconda安装 点击👉https://www.anaconda.com/download, 点击Mac系统安装包, 选择Mac芯片:苹果芯片 or intel芯片, 选择苹果芯片图形界面安装&#x…...

第3篇:数据库路由模块设计与 SQL 路由策略解析
3.1 什么是数据库路由? 在分库分表或多数据库实例架构中,**数据库路由模块(SQL Router)**的作用是: 将客户端发来的 SQL 请求路由到正确的后端数据库实例或分片表中执行。 它是数据库中间件的核心组件之一。 3.2 数据…...

ARINC818编解码设计FPGA实现
一、设计内容 1.基于xilinx平台进行系列产品设计 2.基于GT高速进行进行设计 3.提供良好的技术支持和售后服务 4.比较详细的代码注释 二、模块设计内容 1.模块顶层设计 2.编码模块部分设计 内容包括: 帧信息产生/ojbect0帧格式产生和发送/object2_object3帧格式产生…...

微软PowerBI考试 PL300-Power BI 入门
Power BI 入门 上篇更新了微软PowerBI考试 PL-300学习指南,今天分享PowerBI入门学习内容。 简介 Microsoft Power BI 是一个完整的报表解决方案,通过开发工具和联机平台提供数据准备、数据可视化、分发和管理。 Power BI 可以从使用单个数据源的简单…...
逻辑回归知识点
一、逻辑回归概念 逻辑回归(Logistic Regression)是一种广泛应用于分类问题的统计方法,尤其适用于二分类问题。 注意: 尽管名称中有"回归"二字,但它实际上是一种分类算法。 解决二分类的问题。 API:sklearn.linear_model.Logis…...
