Python微积分可视化:从导数到积分的交互式教学工具
Python微积分可视化:从导数到积分的交互式教学工具
一、引言
微积分是理解自然科学的基础,但抽象的导数、积分概念常让初学者感到困惑。本文基于Matplotlib开发一套微积分可视化工具,通过动态图像直观展示导数的几何意义、积分的近似计算及跨学科应用,帮助读者建立"数值-图形-物理意义"的多维认知。
二、导数可视化:切线与变化率
2.1 导数的几何意义
导数表示函数在某点的瞬时变化率,几何上对应函数图像在该点的切线斜率。
核心公式:
f ′ ( x 0 ) = lim h → 0 f ( x 0 + h ) − f ( x 0 ) h f'(x_0) = \lim_{h \to 0} \frac{f(x_0+h) - f(x_0)}{h} f′(x0)=h→0limhf(x0+h)−f(x0)
2.2 单一点导数可视化
def plot_derivative(f, df, x_range=(-5, 5), x0=1):# 生成函数数据x = np.linspace(x_range[0], x_range[1], 500)y = f(x)# 绘制原函数plt.plot(x, y, "b-", label=f"$f(x) = {get_function_label(f)}$")# 计算切线y0 = f(x0)slope = df(x0)tangent_x = np.linspace(x0-1.5, x0+1.5, 50)tangent_y = slope*(tangent_x - x0) + y0plt.plot(tangent_x, tangent_y, "r--", label=f"切线: 斜率={slope:.2f}")# 标记切点plt.plot(x0, y0, "ro", markersize=8)plt.annotate(f"切点: ({x0:.1f}, {y0:.1f})", xy=(x0,y0), xytext=(x0+0.5,y0-1), arrowprops=dict(arrowstyle="->"))
示例:二次函数f(x)=x²在x=1.5处的导数
def f_quad(x): return x**2
def df_quad(x): return 2*x
plot_derivative(f_quad, df_quad, x0=1.5)

2.3 动态切线动画
通过FuncAnimation展示切点移动时切线的变化,直观理解导数值的连续性。
def create_tangent_animation(f, df, x_range=(-3,3)):x0_values = np.linspace(x_range[0]+0.5, x_range[1]-0.5, 30)fig, ax = plt.subplots()# 初始化图像元素function_line, = ax.plot([], [], "b-", label="f(x)")tangent_line, = ax.plot([], [], "r--", label="切线")point, = ax.plot([], [], "ro")def update(frame):x0 = x0_values[frame]y0 = f(x0)slope = df(x0)# 更新切线数据tangent_x = np.linspace(x0-1.2, x0+1.2, 50)tangent_y = slope*(tangent_x - x0) + y0tangent_line.set_data(tangent_x, tangent_y)# 更新切点point.set_data(x0, y0)return tangent_line, pointanim = FuncAnimation(fig, update, frames=len(x0_values), interval=200)anim.save("tangent_animation.gif", writer="pillow")
正弦函数切线动画效果

三、积分可视化:面积与累积量
3.1 黎曼和:积分的数值逼近
通过矩形面积之和近似函数下方的面积,分为左端点、右端点、中点三种方法。
核心公式:
∫ a b f ( x ) d x ≈ ∑ i = 1 n f ( x i ∗ ) Δ x \int_a^b f(x)dx \approx \sum_{i=1}^n f(x_i^*)\Delta x ∫abf(x)dx≈i=1∑nf(xi∗)Δx
3.2 黎曼和可视化函数
def plot_riemann_sum(f, interval=(0,2), n_rectangles=5, method="left"):a, b = intervaldx = (b - a)/n_rectangles# 绘制函数曲线x = np.linspace(a-0.5, b+0.5, 500)plt.plot(x, f(x), "b-", label=f"$f(x) = {get_function_label(f)}$")# 绘制矩形for i in range(n_rectangles):x_left = a + i*dxx_right = x_left + dxif method == "left": x_val = x_leftelif method == "right": x_val = x_rightelse: x_val = (x_left + x_right)/2height = f(x_val)rect = plt.Rectangle((x_left, 0), dx相关文章:

Python微积分可视化:从导数到积分的交互式教学工具
Python微积分可视化:从导数到积分的交互式教学工具 一、引言 微积分是理解自然科学的基础,但抽象的导数、积分概念常让初学者感到困惑。本文基于Matplotlib开发一套微积分可视化工具,通过动态图像直观展示导数的几何意义、积分的近似计算及跨学科应用,帮助读者建立"数…...

Juce实现Table自定义
Juce实现Table自定义 一.总体展示概及概述 在项目中Juce中TableList往往无法满足用户需求,头部和背景及背景颜色设置以及在Cell中添加自定义按钮,所以需要自己实现自定义TabelList,该示例是展示实现自定义TableList,实现自定义标…...

【25.06】fabric进行caliper测试加环境部署
前置条件 安装一个Ubuntu20+的镜像 基础环境安装 Git cURL vim jq sudo apt install -y git curl vim jq Docker和Docker-compose 这个命令会自动安装docker sudo apt install docker-compose sudo chmod +x /usr/bin/docker-compose docker versiondocker-compose vers…...

【后端高阶面经:架构篇】51、搜索引擎架构与排序算法:面试关键知识点全解析
一、搜索引擎核心基石:倒排索引技术深度解析 (一)倒排索引的本质与构建流程 倒排索引(Inverted Index)是搜索引擎实现快速检索的核心数据结构,与传统数据库的正向索引(文档→关键词࿰…...

Windows应用-音视频捕获
下载“Windows应用-音视频捕获”项目 本应用可以同时捕获4个视频源和4个音频源,可以监视视频源图像,监听音频源;可以将视频源图像写入MP4文件,将音频源写入MP3或WAV文件;还可以录制系统播放的声音。本应用使用MFC对话框…...
【OCCT+ImGUI系列】012-Geom2d_AxisPlacement
Geom2d_AxisPlacement 教学笔记 一、类概述 Geom2d_AxisPlacement 表示二维几何空间中的一个坐标轴(轴系),由两部分组成: gp_Pnt2d:原点(Location)gp_Dir2d:单位方向向量ÿ…...

优化WP外贸建站提升用户体验
WordPress作为一个强大的建站工具,通过合理的优化,可以提升用户体验,吸引更多潜在客户。本文将为您介绍一些优化WordPress外贸建站的实用建议。 1. 响应式设计 随着移动设备的普及,确保您的WordPress网站具有响应式设计变得至关…...

【C++高并发内存池篇】性能卷王养成记:C++ 定长内存池,让内存分配快到飞起!
📝本篇摘要 在本篇将介绍C定长内存池的概念及实现问题,引入内存池技术,通过实现一个简单的定长内存池部分,体会奥妙所在,进而为之后实现整体的内存池做铺垫! 🏠欢迎拜访🏠ÿ…...

mac下通过anaconda安装Python
本次分享mac下通过anaconda安装Python、Jupyter Notebook、R。 anaconda安装 点击👉https://www.anaconda.com/download, 点击Mac系统安装包, 选择Mac芯片:苹果芯片 or intel芯片, 选择苹果芯片图形界面安装&#x…...

第3篇:数据库路由模块设计与 SQL 路由策略解析
3.1 什么是数据库路由? 在分库分表或多数据库实例架构中,**数据库路由模块(SQL Router)**的作用是: 将客户端发来的 SQL 请求路由到正确的后端数据库实例或分片表中执行。 它是数据库中间件的核心组件之一。 3.2 数据…...

ARINC818编解码设计FPGA实现
一、设计内容 1.基于xilinx平台进行系列产品设计 2.基于GT高速进行进行设计 3.提供良好的技术支持和售后服务 4.比较详细的代码注释 二、模块设计内容 1.模块顶层设计 2.编码模块部分设计 内容包括: 帧信息产生/ojbect0帧格式产生和发送/object2_object3帧格式产生…...

微软PowerBI考试 PL300-Power BI 入门
Power BI 入门 上篇更新了微软PowerBI考试 PL-300学习指南,今天分享PowerBI入门学习内容。 简介 Microsoft Power BI 是一个完整的报表解决方案,通过开发工具和联机平台提供数据准备、数据可视化、分发和管理。 Power BI 可以从使用单个数据源的简单…...
逻辑回归知识点
一、逻辑回归概念 逻辑回归(Logistic Regression)是一种广泛应用于分类问题的统计方法,尤其适用于二分类问题。 注意: 尽管名称中有"回归"二字,但它实际上是一种分类算法。 解决二分类的问题。 API:sklearn.linear_model.Logis…...

YARN架构解析:大数据资源管理核心
一、YARN的设计目标 解耦资源管理与作业调度:将资源管理(Resource Management)和任务执行(Task Execution)分离,提升集群资源利用率。支持多种计算框架:不再局限于MapRedu…...

嵌入式学习笔记 - freeRTOS在程序开始在任务内创建任务的好处是什么
在FreeRTOS中,程序启动后优先在初始任务(而非main()函数)内创建其他任务是一种常见且推荐的设计模式,其主要优势包括以下几点: 以下来自deepseek的回答,很全面很正确: 🔧 1. 避免…...

Ubuntu22.04 安装 CUDA12.8
1.下载CUDA 由于我装完 Ubuntu22.04 后就自动带了最新的显卡驱动,就没有再去配置驱动。 先查看驱动能支持的CUDA最高版本,这里显示可支持到12.8。 nvidia-smi在CUDA的 说明文档 可查看CUDA对应的驱动版本要求。 在 CUDA Toolkit Archive 查找需要的 …...

Android的uid~package~pid的关系
UID : Linux 系统级用户标识,Android 中每个应用安装时分配唯一 UID(如 1000)。 Package: Android 应用包名(例如android),一个 UID 可关联多个 Package(共享 UID 场景如android:sharedUserI…...

线段树刷题记录
一篇讲解很好的线段树博客:数据结构--线段树篇_数据结构线段树-CSDN博客 一、区间查询 无修改: (一)最值问题: 1.P1816 忠诚 - 洛谷 思路: 模板。 注意: 无。 代码: #include …...

20250530-C#知识:万物之父Object
C#知识:万物之父Object Object类(即object)是所有类的基类,这里面的方法还是需要好好了解一下。 1、Object类 是顶级父类,其他类默认都是Object类的子类(自定义类也会默认继承Object类)可以用O…...
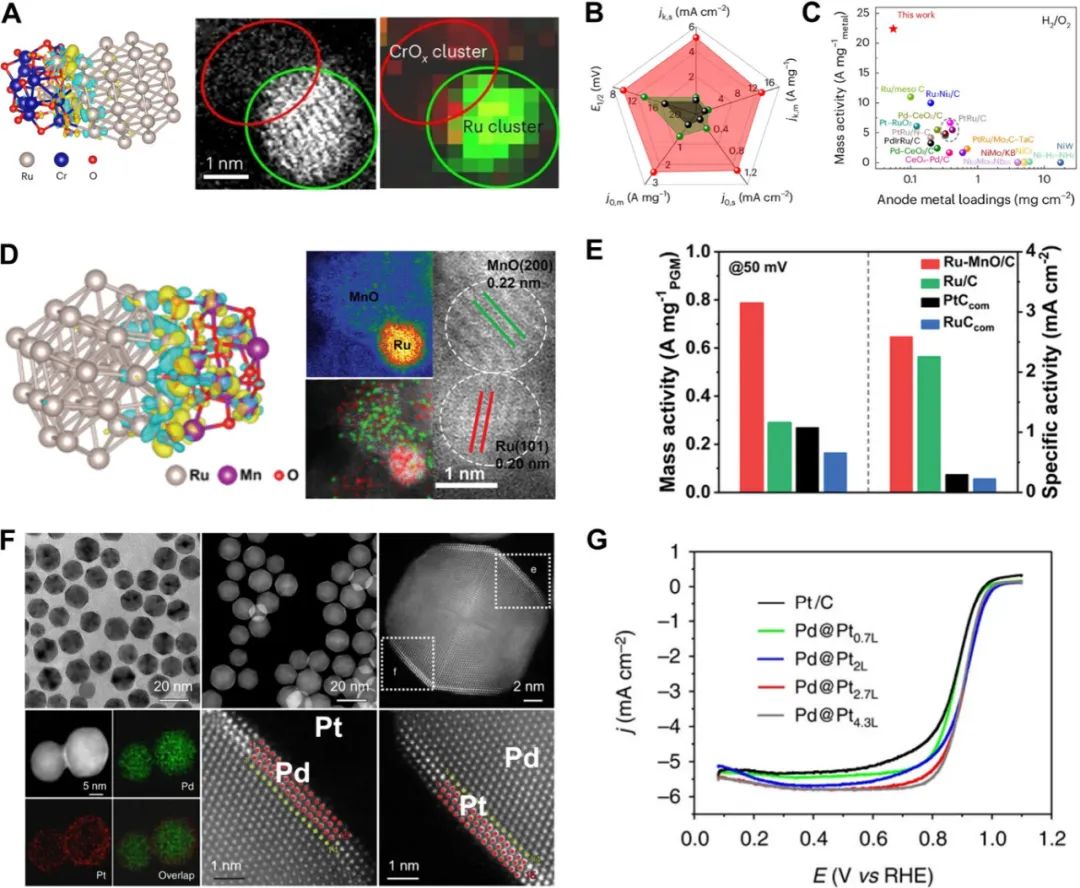
多元素纳米颗粒:开启能源催化新纪元
在能源转型的浪潮中,纳米催化剂正成为推动能源技术突破的关键力量。多元素纳米颗粒(Polyelemental Nanoparticles)凭借其独特的元素协同效应,展现出在能源催化领域的巨大潜力。然而,合成这些复杂体系的纳米颗粒面临着诸…...

分布式锁优化:使用Lua脚本保证释放锁的原子性问题
分布式锁优化(二):使用Lua脚本保证释放锁的原子性问题 💻黑马视频链接:Lua脚本解决多条命令原子性问题 在上一章节视频实现了一个可用的Redis分布式锁,采用SET NX EX命令实现互斥和过期自动释放机制&…...

电脑wifi显示已禁用怎么点都无法启用
一、重启路由器与电脑 有时候,简单的重启可以解决很多小故障。试着先断开电源让路由器休息一会儿再接通;对于电脑,则可选择重启系统看看情况是否有改善。 二、检查驱动程序 无线网卡驱动程序的问题也是导致WiFi无法启用的常见原因之一。我…...

【FPGA开发】Ubuntu16.04环境下配置Vivado2018.3—附软件包
文章目录 环境介绍关键步骤记录安装虚拟机及镜像安装vivadolicense导入 环境介绍 vivado:2018.3 虚拟机:vmware 16 pro 镜像:Ubuntu16.04 64位 所有相关软件压缩包: 链接:https://pan.quark.cn/s/fd2730b46b20 提取码…...

vue-seamless-scroll 结束从头开始,加延时后滚动
今天遇到一个大屏需求: 1️⃣初始进入页面停留5秒,然后开始滚动 2️⃣最后一条数据出现在最后一行时候暂停5秒,然后返回1️⃣ 依次循环,发现vue-seamless-scroll的方法 ScrollEnd是监测最后一条数据消失在第一行才回调ÿ…...
和 MySQL/SQL)
不同的数据库操作方式:MongoDB(NoSQL)和 MySQL/SQL
这两种写法分别使用了不同的数据库操作方式:第一种是 MongoDB(NoSQL) 的写法,第二种是 MySQL/SQL 的写法。我们来对比它们的区别,并给出优化建议。 1. MongoDB(NoSQL)写法 const user await d…...

0-EATSA-GNN:基于图节点分类师生机制的边缘感知和两阶段注意力增强图神经网络(code)
code:https://github.com/afofanah/EATSA-GNN. 文章目录 Abstract1. Introduction1.1.动态图场景1.2.EATSA-GNN框架的背景化2. Background2.1.GNN边缘感知挑战2.2.GNN的可解释性问题2.3.EATSA-GNN可解释性3. Related worksAbstract 图神经网络(GNNs)从根本上改变了我们处理和…...
-spark数据倾斜)
大数据学习(124)-spark数据倾斜
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言📝支持一…...

配置前端控制器
一、DispatcherServlet 详解 在使用 Spring MVC 框架构建 Web 应用时,DispatcherServlet是整个请求处理流程的核心。本文将深入解析DispatcherServlet的作用、工作原理及其在 Spring MVC 架构中的关键地位。 1.DispatcherServlet 是什么? DispatcherS…...

lua注意事项
感觉是lua的一大坑啊,它还不如函数内部就局部变量呢 注意函数等内部,全部给加上local得了...

Git的三种合并方式
在 Gitee(码云)中合并分支主要有三种方式:普通合并(Merge Commit)、压缩合并(Squash Merge)和变基合并(Rebase Merge)。每种方式适用于不同的场景,各有…...
