线段树刷题记录
一篇讲解很好的线段树博客:数据结构--线段树篇_数据结构线段树-CSDN博客
一、区间查询 无修改:
(一)最值问题:
1.P1816 忠诚 - 洛谷
思路:
模板。
注意:
无。
代码:
#include <bits/stdc++.h>#define ioscc ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
#define endl '\n'
#define me(a, x) memset(a, x, sizeof a)
#define all(a) a.begin(), a.end()
#define sz(a) ((int)(a).size())
#define pb(a) push_back(a)
using namespace std;typedef unsigned long long ull;
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<vector<int>> vvi;
typedef vector<int> vi;
typedef vector<bool> vb;const int dx[4] = {-1, 0, 1, 0};
const int dy[4] = {0, 1, 0, -1};
const int MAX = (1ll << 31) - 1;
const int MIN = 1 << 31;
const int MOD = 1e9 + 7;
const int N = 1e5 + 10;template <class T>
ostream &operator<<(ostream &os, const vector<T> &a) noexcept
{for (int i = 0; i < sz(a) - 10; i++)std::cout << a[i] << ' ';return os;
}template <class T>
istream &operator>>(istream &in, vector<T> &a) noexcept
{for (int i = 0; i < sz(a) - 10; i++)std::cin >> a[i];return in;
}/* ----------------- 有乘就强转,前缀和开ll ----------------- */int v[N];
struct Node
{int l, r;int minn;
} tr[N * 4];void pushup(int u)
{tr[u].minn = min(tr[u << 1].minn, tr[u << 1 | 1].minn);
}void build(int u, int l, int r)
{if (l == r){tr[u] = {l, r, v[l]};return;}tr[u] = {l, r};int mid = l + r >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);pushup(u);
}int query(int u, int l, int r)
{if (tr[u].l >= l && tr[u].r <= r){return tr[u].minn;}int mid = tr[u].l + tr[u].r >> 1;int minn = MAX;if (l <= mid)minn = min(minn, query(u << 1, l, r));if (r > mid)minn = min(minn, query(u << 1 | 1, l, r));return minn;
}void solve()
{int n, m;cin >> n >> m;for (int i = 1; i <= n; ++i)cin >> v[i];build(1, 1, n);while (m--){int l, r;cin >> l >> r;cout << query(1, l, r) << ' ';}cout << endl;
}int main()
{ioscc;solve();return 0;
}2.P1886 滑动窗口 /【模板】单调队列 - 洛谷
思路:
模板。
注意:
无。
代码:
#include <bits/stdc++.h>#define ioscc ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
#define endl '\n'
#define me(a, x) memset(a, x, sizeof a)
#define all(a) a.begin(), a.end()
#define sz(a) ((int)(a).size())
#define pb(a) push_back(a)
using namespace std;typedef unsigned long long ull;
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<vector<int>> vvi;
typedef vector<int> vi;
typedef vector<bool> vb;const int dx[4] = {-1, 0, 1, 0};
const int dy[4] = {0, 1, 0, -1};
const int MAX = (1ll << 31) - 1;
const int MIN = 1 << 31;
const int MOD = 1e9 + 7;
const int N = 1e6 + 10;template <class T>
ostream &operator<<(ostream &os, const vector<T> &a) noexcept
{for (int i = 0; i < sz(a) - 10; i++)std::cout << a[i] << ' ';return os;
}template <class T>
istream &operator>>(istream &in, vector<T> &a) noexcept
{for (int i = 0; i < sz(a) - 10; i++)std::cin >> a[i];return in;
}/* ----------------- 有乘就强转,前缀和开ll ----------------- */int v[N];
struct Node
{int l, r;int minn, maxx;
} tr[N * 4];void pushup(int u)
{tr[u].minn = min(tr[u << 1].minn, tr[u << 1 | 1].minn);tr[u].maxx = max(tr[u << 1].maxx, tr[u << 1 | 1].maxx);
}void build(int u, int l, int r)
{if (l == r){tr[u] = {l, r, v[l], v[l]};return;}tr[u] = {l, r, 0, 0};int mid = l + r >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);pushup(u);
}int queryMin(int u, int l, int r)
{if (tr[u].l >= l && tr[u].r <= r){return tr[u].minn;}int mid = tr[u].l + tr[u].r >> 1;int minn = MAX;if (l <= mid)minn = min(minn, queryMin(u << 1, l, r));if (r > mid)minn = min(minn, queryMin(u << 1 | 1, l, r));return minn;
}int queryMax(int u, int l, int r)
{if (tr[u].l >= l && tr[u].r <= r){return tr[u].maxx;}int mid = tr[u].l + tr[u].r >> 1;int maxx = MIN;if (l <= mid)maxx = max(maxx, queryMax(u << 1, l, r));if (r > mid)maxx = max(maxx, queryMax(u << 1 | 1, l, r));return maxx;
}void solve()
{int n, k;cin >> n >> k;for (int i = 1; i <= n; ++i)cin >> v[i];build(1, 1, n);for (int i = 1; i <= n - k + 1; ++i)cout << queryMin(1, i, i + k - 1) << ' ';cout << endl;for (int i = 1; i <= n - k + 1; ++i)cout << queryMax(1, i, i + k - 1) << ' ';cout << endl;
}int main()
{ioscc;solve();return 0;
}二、区间查询 单点修改:
(一)区间和问题:
1.P2068 统计和 - 洛谷
思路:
模板。
注意:
无。
代码:
#include <bits/stdc++.h>#define ioscc ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
#define endl '\n'
#define me(a, x) memset(a, x, sizeof a)
#define all(a) a.begin(), a.end()
#define sz(a) ((int)(a).size())
#define pb(a) push_back(a)
using namespace std;typedef unsigned long long ull;
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<vector<int>> vvi;
typedef vector<int> vi;
typedef vector<bool> vb;const int dx[4] = {-1, 0, 1, 0};
const int dy[4] = {0, 1, 0, -1};
const int MAX = (1ll << 31) - 1;
const int MIN = 1 << 31;
const int MOD = 1e9 + 7;
const int N = 1e5 + 10;template <class T>
ostream &operator<<(ostream &os, const vector<T> &a) noexcept
{for (int i = 0; i < sz(a) - 10; i++)std::cout << a[i] << ' ';return os;
}template <class T>
istream &operator>>(istream &in, vector<T> &a) noexcept
{for (int i = 0; i < sz(a) - 10; i++)std::cin >> a[i];return in;
}/* ----------------- 有乘就强转,前缀和开ll ----------------- */struct Node
{int l, r;ll sum;
} tr[N * 4];void pushup(int u)
{tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}void build(int u, int l, int r)
{if (l == r){tr[u] = {l, r, 0};return;}tr[u] = {l, r, 0};int mid = l + r >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);pushup(u);
}ll query(int u, int l, int r)
{if (tr[u].l >= l && tr[u].r <= r)return tr[u].sum;int mid = tr[u].l + tr[u].r >> 1;ll sum = 0;if (l <= mid)sum += query(u << 1, l, r);if (r > mid)sum += query(u << 1 | 1, l, r);return sum;
}void update(int u, int x, int v)
{if (tr[u].l == x && tr[u].r == x)tr[u].sum += v;else{int mid = tr[u].l + tr[u].r >> 1;if (x <= mid)update(u << 1, x, v);elseupdate(u << 1 | 1, x, v);pushup(u);}
}void solve()
{int n, m;cin >> n >> m;build(1, 1, n);while (m--){char op;int a, b;cin >> op >> a >> b;if (op == 'x')update(1, a, b);elsecout << query(1, a, b) << endl;}
}int main()
{ioscc;solve();return 0;
}2.P2184 贪婪大陆 - 洛谷
思路:
区间修改时使用一种类差分的思想,每次埋地雷的时候只在区间左右端点累加一次值,这样就将问题装换为了单点修改;查询时我们再使用前缀和思想统计区间 [l, r] 区间内的地雷数。具体实现就是使用线段树维护两个sum,既区间左端点的地雷和区间右端点的地雷;在查询区间 [l ,r] 时,就可以用 [1, r] 的起点数减去 [1, l] 的终点数。
注意:
无。
代码:
#include <bits/stdc++.h>#define ioscc ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
#define endl '\n'
#define me(a, x) memset(a, x, sizeof a)
#define all(a) a.begin(), a.end()
#define sz(a) ((int)(a).size())
#define pb(a) push_back(a)
#define ls u << 1
#define rs u << 1 | 1
using namespace std;typedef unsigned long long ull;
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<vector<int>> vvi;
typedef vector<int> vi;
typedef vector<bool> vb;const int dx[4] = {-1, 0, 1, 0};
const int dy[4] = {0, 1, 0, -1};
const int MAX = (1ll << 31) - 1;
const int MIN = 1 << 31;
const int MOD = 1e9 + 7;
const int N = 1e5 + 10;template <class T>
ostream &operator<<(ostream &os, const vector<T> &a) noexcept
{for (int i = 0; i < sz(a) - 10; i++)std::cout << a[i] << ' ';return os;
}template <class T>
istream &operator>>(istream &in, vector<T> &a) noexcept
{for (int i = 0; i < sz(a) - 10; i++)std::cin >> a[i];return in;
}/* ----------------- 有乘就强转,前缀和开ll ----------------- */struct Node
{int l, r;int sum[2];
} tr[N * 4];void pushup(int u, int k)
{tr[u].sum[k] = tr[u << 1].sum[k] + tr[u << 1 | 1].sum[k];
}void build(int u, int l, int r)
{tr[u] = {l, r, 0, 0};if (l == r)return;int mid = l + r >> 1;build(u << 1, l, mid);build(u << 1 | 1, mid + 1, r);
}ll query(int u, int l, int r, int k)
{if (tr[u].l >= l && tr[u].r <= r)return tr[u].sum[k];int mid = tr[u].l + tr[u].r >> 1;ll sum = 0;if (l <= mid)sum += query(u << 1, l, r, k);if (r > mid)sum += query(u << 1 | 1, l, r, k);return sum;
}void update(int u, int x, int k)
{if (tr[u].l == tr[u].r){++tr[u].sum[k];return;}int mid = tr[u].l + tr[u].r >> 1;if (x <= mid)update(u << 1, x, k);elseupdate(u << 1 | 1, x, k);pushup(u, k);
}void solve()
{int n, m;cin >> n >> m;build(1, 1, n);while (m--){int op, l, r;cin >> op >> l >> r;if (op == 1)update(1, l, 0), update(1, r, 1);elsecout << query(1, 1, r, 0) - query(1, 1, l - 1, 1) << endl;}
}int main()
{ioscc;solve();return 0;
}(二)最值问题
1.P1198 [JSOI2008] 最大数 - 洛谷
思路:
模板。
注意:
虽然线段树初始为空的,也要初始化 m 个位置为后续做准备。
代码:
#include <bits/stdc++.h>#define ioscc ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
#define endl '\n'
#define me(a, x) memset(a, x, sizeof a)
#define all(a) a.begin(), a.end()
#define sz(a) ((int)(a).size())
#define pb(a) push_back(a)
using namespace std;typedef unsigned long long ull;
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<vector<int>> vvi;
typedef vector<int> vi;
typedef vector<bool> vb;const int dx[4] = {-1, 0, 1, 0};
const int dy[4] = {0, 1, 0, -1};
const int MAX = (1ll << 31) - 1;
const int MIN = -2e18;
const int MOD = 1e9 + 7;
const int N = 2e5 + 10;template <class T>
ostream &operator<<(ostream &os, const vector<T> &a) noexcept
{for (int i = 0; i < sz(a) - 10; i++)std::cout << a[i] << ' ';return os;
}template <class T>
istream &operator>>(istream &in, vector<T> &a) noexcept
{for (int i = 0; i < sz(a) - 10; i++)std::cin >> a[i];return in;
}/* ----------------- 有乘就强转,前缀和开ll ----------------- */struct Node
{int l, r;ll maxx;
} tr[N << 2];void pushup(int u)
{tr[u].maxx = max(tr[u << 1].maxx, tr[u << 1 | 1].maxx);
}void build(int u, int l, int r)
{tr[u] = {l, r, 0};if (l == r)return;int mid = l + r >> 1;build(u << 1, l, mid);build(u << 1 | 1, mid + 1, r);
}ll query(int u, int l, int r)
{if (tr[u].l >= l && tr[u].r <= r)return tr[u].maxx;int mid = tr[u].l + tr[u].r >> 1;ll maxx = MIN;if (l <= mid)maxx = max(maxx, query(u << 1, l, r));if (r > mid)maxx = max(maxx, query(u << 1 | 1, l, r));return maxx;
}void update(int u, int x, int v)
{if (tr[u].l == tr[u].r){tr[u].maxx = v;return;}int mid = tr[u].l + tr[u].r >> 1;if (x <= mid)update(u << 1, x, v);elseupdate(u << 1 | 1, x, v);pushup(u);
}void solve()
{ll n = 0, m;int mod;cin >> m >> mod;build(1, 1, m);int last = 0;while (m--){char op;int x;cin >> op >> x;if (op == 'Q'){last = query(1, n - x + 1, n);cout << last << endl;}else{++n;int ans = ((ll)x + last) % mod;update(1, n, ans);}}
}int main()
{ioscc;solve();return 0;
}三、区间查询 区间修改:
(一)区间和问题:
1.P2357 守墓人 - 洛谷
思路:
模板。
注意:
开ll。
代码:
#include <bits/stdc++.h>#define ioscc ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
#define endl '\n'
#define me(a, x) memset(a, x, sizeof a)
#define all(a) a.begin(), a.end()
#define sz(a) ((int)(a).size())
#define pb(a) push_back(a)
using namespace std;typedef unsigned long long ull;
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<vector<int>> vvi;
typedef vector<int> vi;
typedef vector<bool> vb;const int dx[4] = {-1, 0, 1, 0};
const int dy[4] = {0, 1, 0, -1};
const int MAX = (1ll << 31) - 1;
const int MIN = 1 << 31;
const int MOD = 1e9 + 7;
const int N = 2e5 + 10;template <class T>
ostream &operator<<(ostream &os, const vector<T> &a) noexcept
{for (int i = 0; i < sz(a) - 10; i++)std::cout << a[i] << ' ';return os;
}template <class T>
istream &operator>>(istream &in, vector<T> &a) noexcept
{for (int i = 0; i < sz(a) - 10; i++)std::cin >> a[i];return in;
}/* ----------------- 有乘就强转,前缀和开ll ----------------- */ll v[N];
struct Node
{int l, r;ll sum;ll add;
} tr[N * 4];void pushup(int u)
{tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}void pushdown(int u)
{if (tr[u].add){tr[u << 1].sum += tr[u].add * (tr[u << 1].r - tr[u << 1].l + 1);tr[u << 1 | 1].sum += tr[u].add * (tr[u << 1 | 1].r - tr[u << 1 | 1].l + 1);tr[u << 1].add += tr[u].add;tr[u << 1 | 1].add += tr[u].add;tr[u].add = 0;}
}void build(int u, int l, int r)
{if (l == r){tr[u] = {l, r, v[l], 0};return;}tr[u] = {l, r, 0, 0};int mid = l + r >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);pushup(u);
}ll query(int u, int l, int r)
{if (tr[u].l >= l && tr[u].r <= r)return tr[u].sum;pushdown(u);int mid = tr[u].l + tr[u].r >> 1;ll sum = 0;if (l <= mid)sum += query(u << 1, l, r);if (r > mid)sum += query(u << 1 | 1, l, r);return sum;
}void update(int u, int l, int r, int v)
{if (tr[u].l >= l && tr[u].r <= r){tr[u].sum += (ll)(tr[u].r - tr[u].l + 1) * v;tr[u].add += v;return;}pushdown(u);int mid = tr[u].l + tr[u].r >> 1;if (l <= mid)update(u << 1, l, r, v);if (r > mid)update(u << 1 | 1, l, r, v);pushup(u);
}void solve()
{int n, m;cin >> n >> m;for (int i = 1; i <= n; ++i)cin >> v[i];build(1, 1, n);while (m--){int op;int l, r, v;cin >> op;if (op == 1){cin >> l >> r >> v;update(1, l, r, v);}else if (op == 2){cin >> v;update(1, 1, 1, v);}else if (op == 3){cin >> v;update(1, 1, 1, -v);}else if (op == 4){cin >> l >> r;cout << query(1, l, r) << endl;}elsecout << query(1, 1, 1) << endl;}
}int main()
{ioscc;solve();return 0;
}(二)区间最值+区间和问题:
1.P3130 [USACO15DEC] Counting Haybale P - 洛谷
思路:
线段树维护区间、最小值、区间和、懒标记。
注意:
更新懒标记时也需将节点的最小值加上懒标记的值。
代码:
#include <bits/stdc++.h>#define ioscc ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
#define endl '\n'
#define me(a, x) memset(a, x, sizeof a)
#define all(a) a.begin(), a.end()
#define sz(a) ((int)(a).size())
#define pb(a) push_back(a)
using namespace std;typedef unsigned long long ull;
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<vector<int>> vvi;
typedef vector<int> vi;
typedef vector<bool> vb;const int dx[4] = {-1, 0, 1, 0};
const int dy[4] = {0, 1, 0, -1};
const int MAX = (1ll << 31) - 1;
const int MIN = 1 << 31;
const int MOD = 1e9 + 7;
const int N = 2e5 + 10;template <class T>
ostream &operator<<(ostream &os, const vector<T> &a) noexcept
{for (int i = 0; i < sz(a) - 10; i++)std::cout << a[i] << ' ';return os;
}template <class T>
istream &operator>>(istream &in, vector<T> &a) noexcept
{for (int i = 0; i < sz(a) - 10; i++)std::cin >> a[i];return in;
}/* ----------------- 有乘就强转,前缀和开ll ----------------- */ull v[N];
struct Node
{int l, r;ull minn;ull sum;ull add;
} tr[N * 4];void pushup(int u)
{tr[u].minn = min(tr[u << 1].minn, tr[u << 1 | 1].minn);tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}void pushdown(int u)
{if (tr[u].add){tr[u << 1].sum += tr[u].add * (tr[u << 1].r - tr[u << 1].l + 1);tr[u << 1 | 1].sum += tr[u].add * (tr[u << 1 | 1].r - tr[u << 1 | 1].l + 1);tr[u << 1].minn += tr[u].add;tr[u << 1 | 1].minn += tr[u].add;tr[u << 1].add += tr[u].add;tr[u << 1 | 1].add += tr[u].add;tr[u].add = 0;}
}void build(int u, int l, int r)
{if (l == r){tr[u] = {l, r, v[l], v[l], 0};return;}tr[u] = {l, r, 0, 0, 0};int mid = l + r >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);pushup(u);
}ull querySum(int u, int l, int r)
{if (tr[u].l >= l && tr[u].r <= r){return tr[u].sum;}pushdown(u);int mid = tr[u].l + tr[u].r >> 1;ull sum = 0;if (l <= mid)sum += querySum(u << 1, l, r);if (r > mid)sum += querySum(u << 1 | 1, l, r);return sum;
}ull queryMin(int u, int l, int r)
{if (tr[u].l >= l && tr[u].r <= r){return tr[u].minn;}pushdown(u);int mid = tr[u].l + tr[u].r >> 1;ull minn = MAX;if (l <= mid)minn = min(minn, queryMin(u << 1, l, r));if (r > mid)minn = min(minn, queryMin(u << 1 | 1, l, r));return minn;
}void update(int u, int l, int r, int v)
{if (tr[u].l >= l && tr[u].r <= r){tr[u].sum += (ull)(tr[u].r - tr[u].l + 1) * v;tr[u].minn += v;tr[u].add += v;return;}pushdown(u);int mid = tr[u].l + tr[u].r >> 1;if (l <= mid)update(u << 1, l, r, v);if (r > mid)update(u << 1 | 1, l, r, v);pushup(u);
}void solve()
{int n, m;cin >> n >> m;for (int i = 1; i <= n; ++i)cin >> v[i];build(1, 1, n);while (m--){char op;int a, b, c;cin >> op;if (op == 'M'){cin >> a >> b;cout << queryMin(1, a, b) << endl;}else if (op == 'P'){cin >> a >> b >> c;update(1, a, b, c);}else{cin >> a >> b;cout << querySum(1, a, b) << endl;}}
}int main()
{ioscc;solve();return 0;
}(三)区间和+区间乘
1.P3373 【模板】线段树 2 - 洛谷
思路:
维护乘和加两个懒标记,由于乘法优先级高于加法,所以当前节点的值为 sum * mul + add,
当父节点下传懒标记时,设 m,a 为父节点下传的乘法与加法懒标记,所以当前节点值为 (sum *
mul + add) * m + a,可得 sum * mul * m + add * m + a ,所以mul和sum的更新值为 mul = mul
* m,add = add * m + a。
注意:
开ll,乘和加的优先级。
代码:
#include <bits/stdc++.h>#define ioscc ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
#define endl '\n'
#define me(a, x) memset(a, x, sizeof a)
#define all(a) a.begin(), a.end()
#define sz(a) ((int)(a).size())
#define pb(a) push_back(a)
using namespace std;typedef unsigned long long ull;
typedef long long ll;
typedef pair<int, int> pii;
typedef vector<vector<int>> vvi;
typedef vector<int> vi;
typedef vector<bool> vb;const int dx[4] = {-1, 0, 1, 0};
const int dy[4] = {0, 1, 0, -1};
const int MAX = (1ll << 31) - 1;
const int MIN = 1 << 31;
const int MOD = 1e9 + 7;
const int N = 1e5 + 10;template <class T>
ostream &operator<<(ostream &os, const vector<T> &a) noexcept
{for (int i = 0; i < sz(a) - 10; i++)std::cout << a[i] << ' ';return os;
}template <class T>
istream &operator>>(istream &in, vector<T> &a) noexcept
{for (int i = 0; i < sz(a) - 10; i++)std::cin >> a[i];return in;
}/* ----------------- 有乘就强转,前缀和开ll ----------------- */int mod;
ll v[N];
struct Node
{int l, r;ll sum;ll add, mul;
} tr[N << 2];void pushup(int u)
{tr[u].sum = (tr[u << 1].sum + tr[u << 1 | 1].sum) % mod;
}void calc(Node &t, ll m, ll a)
{t.sum = (t.sum * m % mod + (t.r - t.l + 1) * a % mod) % mod;t.mul = t.mul * m % mod;t.add = (t.add * m + a) % mod;
}void pushdown(int u)
{calc(tr[u << 1], tr[u].mul, tr[u].add);calc(tr[u << 1 | 1], tr[u].mul, tr[u].add);tr[u].add = 0;tr[u].mul = 1;
}void build(int u, int l, int r)
{if (l == r){tr[u] = {l, r, v[l], 0, 1};return;}tr[u] = {l, r, 0, 0, 1};int mid = l + r >> 1;build(u << 1, l, mid);build(u << 1 | 1, mid + 1, r);pushup(u);
}ll query(int u, int l, int r)
{if (tr[u].l >= l && tr[u].r <= r){return tr[u].sum % mod;}pushdown(u);int mid = tr[u].l + tr[u].r >> 1;ll sum = 0;if (l <= mid)sum += query(u << 1, l, r) % mod;if (r > mid)sum += query(u << 1 | 1, l, r) % mod;return sum % mod;
}void update(int u, int l, int r, int m, int a)
{if (tr[u].l >= l && tr[u].r <= r){calc(tr[u], m, a);return;}pushdown(u);int mid = tr[u].l + tr[u].r >> 1;if (l <= mid)update(u << 1, l, r, m, a);if (r > mid)update(u << 1 | 1, l, r, m, a);pushup(u);
}void solve()
{int n, m;cin >> n >> m >> mod;for (int i = 1; i <= n; ++i)cin >> v[i];build(1, 1, n);while (m--){int op;int x, y, v;cin >> op >> x >> y;if (op == 1){cin >> v;update(1, x, y, v, 0);}else if (op == 2){cin >> v;update(1, x, y, 1, v);}elsecout << query(1, x, y) % mod << endl;}
}int main()
{ioscc;solve();return 0;
}相关文章:

线段树刷题记录
一篇讲解很好的线段树博客:数据结构--线段树篇_数据结构线段树-CSDN博客 一、区间查询 无修改: (一)最值问题: 1.P1816 忠诚 - 洛谷 思路: 模板。 注意: 无。 代码: #include …...

20250530-C#知识:万物之父Object
C#知识:万物之父Object Object类(即object)是所有类的基类,这里面的方法还是需要好好了解一下。 1、Object类 是顶级父类,其他类默认都是Object类的子类(自定义类也会默认继承Object类)可以用O…...
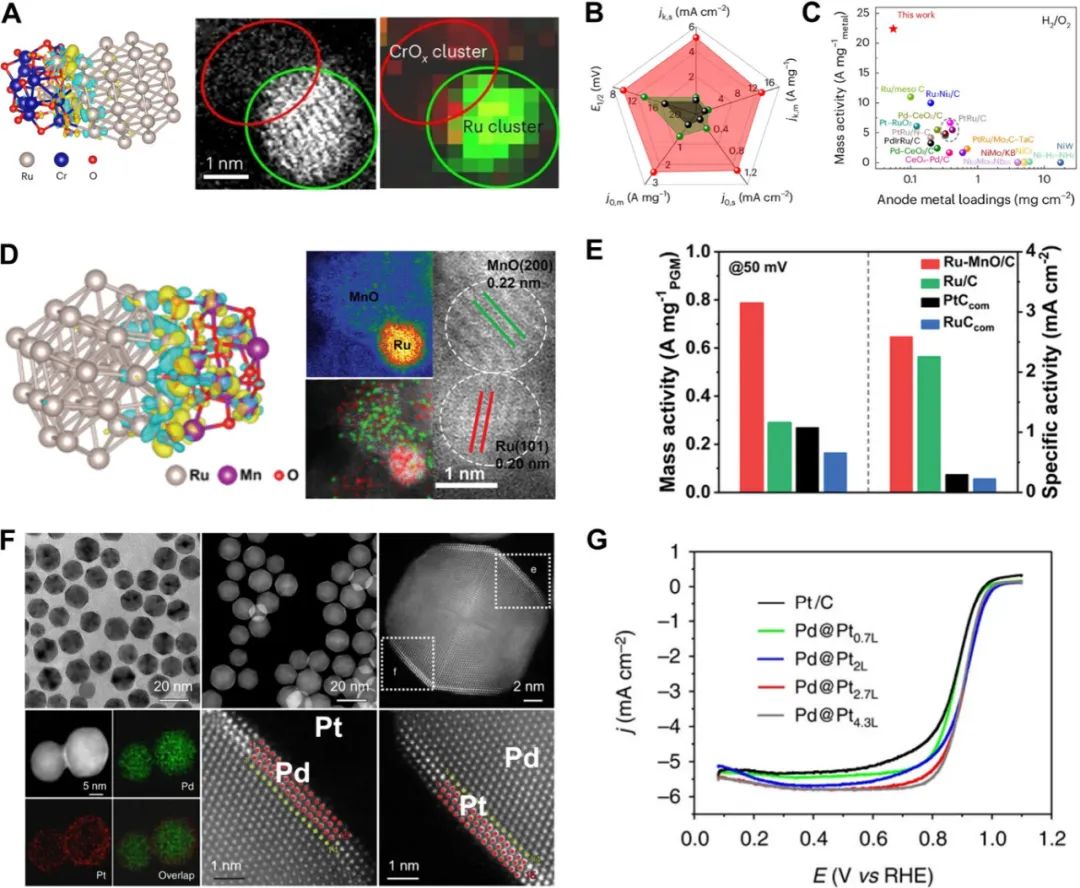
多元素纳米颗粒:开启能源催化新纪元
在能源转型的浪潮中,纳米催化剂正成为推动能源技术突破的关键力量。多元素纳米颗粒(Polyelemental Nanoparticles)凭借其独特的元素协同效应,展现出在能源催化领域的巨大潜力。然而,合成这些复杂体系的纳米颗粒面临着诸…...

分布式锁优化:使用Lua脚本保证释放锁的原子性问题
分布式锁优化(二):使用Lua脚本保证释放锁的原子性问题 💻黑马视频链接:Lua脚本解决多条命令原子性问题 在上一章节视频实现了一个可用的Redis分布式锁,采用SET NX EX命令实现互斥和过期自动释放机制&…...

电脑wifi显示已禁用怎么点都无法启用
一、重启路由器与电脑 有时候,简单的重启可以解决很多小故障。试着先断开电源让路由器休息一会儿再接通;对于电脑,则可选择重启系统看看情况是否有改善。 二、检查驱动程序 无线网卡驱动程序的问题也是导致WiFi无法启用的常见原因之一。我…...

【FPGA开发】Ubuntu16.04环境下配置Vivado2018.3—附软件包
文章目录 环境介绍关键步骤记录安装虚拟机及镜像安装vivadolicense导入 环境介绍 vivado:2018.3 虚拟机:vmware 16 pro 镜像:Ubuntu16.04 64位 所有相关软件压缩包: 链接:https://pan.quark.cn/s/fd2730b46b20 提取码…...

vue-seamless-scroll 结束从头开始,加延时后滚动
今天遇到一个大屏需求: 1️⃣初始进入页面停留5秒,然后开始滚动 2️⃣最后一条数据出现在最后一行时候暂停5秒,然后返回1️⃣ 依次循环,发现vue-seamless-scroll的方法 ScrollEnd是监测最后一条数据消失在第一行才回调ÿ…...
和 MySQL/SQL)
不同的数据库操作方式:MongoDB(NoSQL)和 MySQL/SQL
这两种写法分别使用了不同的数据库操作方式:第一种是 MongoDB(NoSQL) 的写法,第二种是 MySQL/SQL 的写法。我们来对比它们的区别,并给出优化建议。 1. MongoDB(NoSQL)写法 const user await d…...

0-EATSA-GNN:基于图节点分类师生机制的边缘感知和两阶段注意力增强图神经网络(code)
code:https://github.com/afofanah/EATSA-GNN. 文章目录 Abstract1. Introduction1.1.动态图场景1.2.EATSA-GNN框架的背景化2. Background2.1.GNN边缘感知挑战2.2.GNN的可解释性问题2.3.EATSA-GNN可解释性3. Related worksAbstract 图神经网络(GNNs)从根本上改变了我们处理和…...
-spark数据倾斜)
大数据学习(124)-spark数据倾斜
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言📝支持一…...

配置前端控制器
一、DispatcherServlet 详解 在使用 Spring MVC 框架构建 Web 应用时,DispatcherServlet是整个请求处理流程的核心。本文将深入解析DispatcherServlet的作用、工作原理及其在 Spring MVC 架构中的关键地位。 1.DispatcherServlet 是什么? DispatcherS…...

lua注意事项
感觉是lua的一大坑啊,它还不如函数内部就局部变量呢 注意函数等内部,全部给加上local得了...

Git的三种合并方式
在 Gitee(码云)中合并分支主要有三种方式:普通合并(Merge Commit)、压缩合并(Squash Merge)和变基合并(Rebase Merge)。每种方式适用于不同的场景,各有…...

从零到一:我的技术博客导航(持续更新)
作者:冰茶 最后更新:2025年6月3日 本文收录了我的C#编程学习心得与技术探索,将持续更新 前言 作为一名.NET开发者,C#语言的学习与探索一直是我技术成长的核心路径。本文集整理了我在C#学习过程中的思考与实践,希望能够…...

SpringBoot整合Flowable【08】- 前后端如何交互
引子 在第02篇中,我通过 Flowable-UI 绘制了一个简单的绩效流程,并在后续章节中基于这个流程演示了 Flowable 的各种API调用。然而,在实际业务场景中,如果要求前端将用户绘制的流程文件发送给后端再进行解析处理,这种…...

DM达梦数据库开启SQL日志记录功能
DM达梦数据库开启SQL日志记录功能 配置SQL日志(非必须的配置步骤,与主备集群配置无关,如果没有需求可以跳过配置SQL日志) sqllog.ini 配置文件用于SQL日志的配置,当且仅当 INI(dm.ini) 参数 SV…...
)
00 QEMU源码分析中文注释与架构讲解(v8.2.4版本)
QEMU-v8.2.4源码中文注释与架构讲解 文档会不定期更新 注释作者将狼才鲸创建日期2025-05-30更新日期2025-06-02 CSDN阅读地址:QEMU源码中文注释与架构讲解Gitee源码仓库地址:才鲸嵌入式/qemu 一、前言 其它参考教程的网址: QEMU 源码目录…...

【五模型时间序列预测对比】Transformer-LSTM、Transformer、CNN-LSTM、LSTM、CNN
【五模型时间序列预测对比】Transformer-LSTM、Transformer、CNN-LSTM、LSTM、CNN 目录 【五模型时间序列预测对比】Transformer-LSTM、Transformer、CNN-LSTM、LSTM、CNN预测效果基本介绍程序设计参考资料 预测效果 基本介绍 Transformer-LSTM、Transformer、CNN-LSTM、LSTM、…...

深入了解MCP基础与架构
一、引言 在人工智能技术以指数级速度渗透各行业领域的今天,我们正站在一个关键的技术拐点。当ChatGPT月活突破亿级、Gemini Pro实现多模态实时交互、Claude 3.5 Sonnet突破百万上下文长度,这些里程碑事件背后,一个崭新的大门逐步打开&#…...

实验设计与分析(第6版,Montgomery)第5章析因设计引导5.7节思考题5.13 R语言解题
本文是实验设计与分析(第6版,Montgomery著,傅珏生译) 第5章析因设计引导5.7节思考题5.13 R语言解题。主要涉及方差分析,正态假设检验,残差分析,交互作用图。 dataframe<-data.frame( yc(36,18,30,39,20…...

怎么选择合适的高防IP
选择合适的高防IP需要综合考虑业务需求、防护能力、服务稳定性、成本效益等多方面因素。以下是从多个权威来源整理的关键要点,帮助您做出科学决策: 一、明确业务需求 业务类型与规模 网站/应用类:需支持HTTP/HTTPS协议,并配置域名…...

【java面试】MySQL篇
MySQL篇 一、总体结构二、优化(一)定位慢查询1.1 开源工具1.2Mysql自带的慢日志查询1.3 总结 (二)定位后优化2.1 优化2.2 总结 (三)索引3.1 索引3.2 索引底层数据结构——B树3.3 总结 (四&#…...

贪心算法应用:欧拉路径(Fleury算法)详解
Java中的贪心算法应用:欧拉路径(Fleury算法)详解 一、欧拉路径与欧拉回路基础 1.1 基本概念 欧拉路径(Eulerian Path)是指在一个图中,经过图中每一条边且每一条边只经过一次的路径。如果这条路径的起点和…...

【算法设计与分析】实验——二维0-1背包问题(算法分析题:算法思路),独立任务最优调度问题(算法实现题:实验过程,描述,小结)
说明:博主是大学生,有一门课是算法设计与分析,这是博主记录课程实验报告的内容,题目是老师给的,其他内容和代码均为原创,可以参考学习,转载和搬运需评论吱声并注明出处哦。 要求:3-…...

P12592题解
题目传送门 思路 由于题目中说了可以任意交换两个字符的位置,我们只需要判断这个字符串是否满足回文串的条件即可。 代码: #include<bits/stdc.h> using namespace std; int a[30]; int main(){int T;cin>>T;while(T--){fill(a,a29,0);/…...
:分解与复用命令)
ffmpeg命令(二):分解与复用命令
分解(Demuxing) 提取视频流(不含音频) ffmpeg -i input.mp4 -an -vcodec copy video.h264-an:去掉音频 -vcodec copy:拷贝视频码流,不重新编码 提取音频流(不含视频)…...

【Git】View Submitted Updates——diff、show、log
在 Git 中查看更新的内容(即工作区、暂存区或提交之间的差异)是日常开发中的常见操作。以下是常用的命令和场景说明: 文章目录 1、查看工作区与暂存区的差异2、查看提交历史中的差异3、查看工作区与最新提交的差异4、查看两个提交之间的差异5…...

deepseek原理和项目实战笔记2 -- deepseek核心架构
混合专家(MoE) 混合专家(Mixture of Experts, MoE) 是一种机器学习模型架构,其核心思想是通过组合多个“专家”子模型(通常为小型神经网络)来处理不同输入,从而提高模型的容…...

在 MATLAB 2015a 中如何调用 Python
在 MATLAB 2015a 中调用 Python 可通过系统命令调用、.NET 交互层包装、MEX 接口间接桥接、环境变量配置四种方式,但因该版本对 Python 支持有限,主要依赖的是系统命令调用与间接脚本交互。其中,通过 system() 函数调用 Python 脚本是最简单且…...

房屋租赁系统 Java+Vue.js+SpringBoot,包括房屋类型、房屋信息、预约看房、合同信息、房屋报修、房屋评价、房主管理模块
房屋租赁系统 JavaVue.jsSpringBoot,包括房屋类型、房屋信息、预约看房、合同信息、房屋报修、房屋评价、房主管理模块 百度云盘链接:https://pan.baidu.com/s/1KmwOFzN9qogyaLQei3b6qw 密码:l2yn 摘 要 社会的发展和科学技术的进步…...
