【机器学习基础】机器学习入门核心算法:Mini-Batch K-Means算法

机器学习入门核心算法:Mini-Batch K-Means算法
- 一、算法逻辑
- 工作流程
- 与传统K-Means对比
- 二、算法原理与数学推导
- 1. 目标函数
- 2. Mini-Batch更新规则
- 3. 学习率衰减机制
- 4. 伪代码
- 三、模型评估
- 1. 内部评估指标
- 2. 收敛性判断
- 3. 超参数调优
- 四、应用案例
- 1. 图像处理 - 颜色量化
- 2. 用户分群 - 电商推荐
- 3. 异常检测 - 网络安全
- 五、面试题及答案
- 1. Q:为什么Mini-Batch K-Means比传统K-Means快?
- 2. Q:如何选择批大小b?
- 3. Q:学习率 η t = 1 / ( s k + 1 ) \eta_t = 1/(s_k+1) ηt=1/(sk+1) 的设计原理?
- 4. Q:何时不适合使用Mini-Batch版本?
- 六、相关论文
- 七、优缺点对比
- 总结
一、算法逻辑
Mini-Batch K-Means 是传统K-Means算法的优化版本,专为大规模数据集设计。其核心思想是:每次迭代仅使用数据集的随机子集(mini-batch)来更新聚类中心,而非整个数据集。这种方法在保持聚类质量的同时,显著降低计算复杂度和内存需求。
工作流程
与传统K-Means对比
| 特性 | 传统K-Means | Mini-Batch K-Means |
|---|---|---|
| 数据使用 | 全数据集 | 随机子集(mini-batch) |
| 计算复杂度 | O(T·n·K·d) | O(T·b·K·d) |
| 内存需求 | 高(需加载全数据) | 低(仅需小批量数据) |
| 收敛速度 | 较慢 | 快3-5倍 |
| 适用数据规模 | 中小型数据集 | 大规模数据集(>10^5) |
注:T=迭代次数,n=样本数,K=聚类数,d=特征维度,b=批大小
二、算法原理与数学推导
1. 目标函数
同K-Means,最小化簇内平方和(Within-Cluster Sum of Squares, WCSS):
J = ∑ k = 1 K ∑ x ∈ C k ∥ x − μ k ∥ 2 J = \sum_{k=1}^K \sum_{x \in C_k} \|x - \mu_k\|^2 J=k=1∑Kx∈Ck∑∥x−μk∥2
其中 μ k \mu_k μk 是簇 C k C_k Ck 的中心。
2. Mini-Batch更新规则
对于每个mini-batch B t B_t Bt:
-
样本分配:对 x i ∈ B t x_i \in B_t xi∈Bt,计算最近中心:
c ( t ) ( x i ) = arg min k ∥ x i − μ k ( t ) ∥ 2 c^{(t)}(x_i) = \arg\min_k \|x_i - \mu_k^{(t)}\|^2 c(t)(xi)=argkmin∥xi−μk(t)∥2 -
中心更新:对每个簇 k k k,更新中心为历史分配的加权平均:
μ k ( t + 1 ) = μ k ( t ) + η t ⋅ ( 1 ∣ C k ∩ B t ∣ ∑ x i ∈ C k ∩ B t x i − μ k ( t ) ) \mu_k^{(t+1)} = \mu_k^{(t)} + \eta_t \cdot \left( \frac{1}{|C_k \cap B_t|} \sum_{x_i \in C_k \cap B_t} x_i - \mu_k^{(t)} \right) μk(t+1)=μk(t)+ηt⋅(∣Ck∩Bt∣1xi∈Ck∩Bt∑xi−μk(t))
其中 η t \eta_t ηt 是学习率,通常设置为:
η t = 1 s k + 1 \eta_t = \frac{1}{s_k + 1} ηt=sk+11
s k s_k sk 是历史上分配到簇 k k k 的样本总数(随时间累积)
3. 学习率衰减机制
为平衡早期快速收敛和后期稳定性:
s k ← s k + n k ( t ) s_k \leftarrow s_k + n_k^{(t)} sk←sk+nk(t)
其中 n k ( t ) = ∣ { x i ∈ B t : c ( t ) ( x i ) = k } ∣ n_k^{(t)} = |\{x_i \in B_t : c^{(t)}(x_i) = k\}| nk(t)=∣{xi∈Bt:c(t)(xi)=k}∣
4. 伪代码
输入: 数据集 X, 聚类数 K, 批大小 b, 最大迭代次数 T
输出: 聚类中心 {μ₁, μ₂, ..., μ_K}
1. 初始化中心 μ_k (随机或K-Means++)
2. 初始化计数器 s_k = 0 for k=1..K
3. for t=1 to T:
4. 随机采样 mini-batch B_t ⊂ X, |B_t|=b
5. 对每个 x_i ∈ B_t:
6. c(x_i) = argmin_k ||x_i - μ_k||² // 分配样本
7. 对每个簇 k:
8. n_k = |{x_i ∈ B_t : c(x_i)=k}| // 批次中分配数量
9. if n_k > 0:
10. v_k = (1/n_k) ∑_{c(x_i)=k} x_i // 批次均值
11. s_k = s_k + n_k // 更新计数器
12. μ_k = μ_k + (n_k/s_k)(v_k - μ_k) // 更新中心
13. 返回 {μ_k}
三、模型评估
1. 内部评估指标
-
轮廓系数(Silhouette Coefficient):
s ( i ) = b ( i ) − a ( i ) max { a ( i ) , b ( i ) } s(i) = \frac{b(i) - a(i)}{\max\{a(i), b(i)\}} s(i)=max{a(i),b(i)}b(i)−a(i)
其中 a ( i ) a(i) a(i) 是样本 i i i 到同簇其他点的平均距离, b ( i ) b(i) b(i) 是到最近其他簇的平均距离。 -
戴维斯-布尔丁指数(Davies-Bouldin Index):
D B = 1 K ∑ k = 1 K max j ≠ k ( σ k + σ j d ( μ k , μ j ) ) DB = \frac{1}{K}\sum_{k=1}^K \max_{j \neq k} \left( \frac{\sigma_k + \sigma_j}{d(\mu_k,\mu_j)} \right) DB=K1k=1∑Kj=kmax(d(μk,μj)σk+σj)
值越小表示聚类效果越好
2. 收敛性判断
- 相对中心移动量:
Δ = 1 K ∑ k = 1 K ∥ μ k ( t ) − μ k ( t − 1 ) ∥ 2 < ϵ \Delta = \frac{1}{K}\sum_{k=1}^K \|\mu_k^{(t)} - \mu_k^{(t-1)}\|^2 < \epsilon Δ=K1k=1∑K∥μk(t)−μk(t−1)∥2<ϵ
通常 ϵ = 10 − 5 \epsilon = 10^{-5} ϵ=10−5
3. 超参数调优
| 参数 | 推荐值 | 影响 |
|---|---|---|
| 批大小 (b) | 50 × K 50 \times K 50×K | 过小→不稳定;过大→速度慢 |
| 最大迭代次数 | 100-500 | 根据收敛曲线调整 |
| 初始化方法 | K-Means++ | 显著改善聚类质量 |
四、应用案例
1. 图像处理 - 颜色量化
任务:将24位真彩图压缩为256色
流程:
- 将像素RGB值作为特征点( d = 3 d=3 d=3)
- 使用Mini-Batch K-Means( K = 256 K=256 K=256, b = 10 4 b=10^4 b=104)
- 将每个像素映射到最近聚类中心
优势:处理100MP图像仅需10秒(传统K-Means需10分钟)
2. 用户分群 - 电商推荐
场景:为5000万用户分群
特征:RFM(最近购买Recency、频率Frequency、金额Monetary)
实现:
- 聚类数 K = 8 K=8 K=8
- 批大小 b = 50 , 000 b=50,000 b=50,000
- 结果:识别出"高价值流失用户"群体,推送定向优惠券
效果:转化率提升22%
3. 异常检测 - 网络安全
方法:
- 网络流量特征聚类(IP包数、流量大小、连接频率)
- 定义远离所有聚类中心的样本为异常
优势:实时处理10Gb/s流量数据
五、面试题及答案
1. Q:为什么Mini-Batch K-Means比传统K-Means快?
A:计算复杂度从 O ( T ⋅ n ⋅ K ⋅ d ) O(T·n·K·d) O(T⋅n⋅K⋅d) 降为 O ( T ⋅ b ⋅ K ⋅ d ) O(T·b·K·d) O(T⋅b⋅K⋅d),其中 b ≪ n b \ll n b≪n。内存仅需加载小批量数据,减少I/O开销。
2. Q:如何选择批大小b?
A:经验公式 b = 50 × K b = 50 \times K b=50×K:
- K = 10 K=10 K=10 → b ≈ 500 b≈500 b≈500
- K = 100 K=100 K=100 → b ≈ 5000 b≈5000 b≈5000
需权衡:过小导致更新噪声大,过大失去加速意义。
3. Q:学习率 η t = 1 / ( s k + 1 ) \eta_t = 1/(s_k+1) ηt=1/(sk+1) 的设计原理?
A:这是倒数衰减策略:
- 早期 s k s_k sk 小 → η t \eta_t ηt 大 → 快速逼近中心
- 后期 s k s_k sk 大 → η t \eta_t ηt 小 → 精细调整
类似随机梯度下降(SGD)的学习率衰减。
4. Q:何时不适合使用Mini-Batch版本?
A:三种情况:
- 数据量小( n < 10 , 000 n<10,000 n<10,000)时加速不明显
- 需要精确簇边界(如医学诊断)
- 数据分布极度不均衡(小批量可能漏掉稀有类)
六、相关论文
-
奠基性论文:
Sculley, D. (2010). Web-Scale K-Means Clustering. Proceedings of the 19th International Conference on World Wide Web.
贡献:首次提出Mini-Batch K-Means,在Google新闻数据上实现10倍加速 -
理论分析:
Bottou, L., & Bengio, Y. (1995). Convergence Properties of the K-Means Algorithms. Advances in Neural Information Processing Systems.
贡献:证明随机梯度下降在K-Means中的收敛性 -
工业优化:
Newling, J., & Fleuret, F. (2016). Fast K-Means with Accurate Bounds. ICML.
贡献:提出改进的中心更新边界,减少迭代次数30%
七、优缺点对比
| 优点 | 缺点 |
|---|---|
| 计算高效:比传统K-Means快3-10倍 | 解质量略低:WCSS通常高3-5% |
| 内存友好:可处理超大规模数据(>10^9样本) | 对批大小敏感:需调参 |
| 在线学习:支持流式数据逐步更新 | 收敛不稳定:不同运行结果可能差异2-3% |
| 易并行化:batch间相互独立 | 中心初始化敏感:同传统K-Means |
| 实用性强:Spark MLlib等平台原生支持 | 理论保证弱:只能收敛到局部最优 |
总结
Mini-Batch K-Means 通过随机小批量更新策略,在保持可接受聚类质量的前提下,大幅提升计算效率。其核心价值在于:
- 大规模数据处理:轻松应对百万级以上数据集
- 资源效率:内存消耗低,适合受限环境
- 实用便捷:参数少易实现,主流库均有支持
最佳实践:
- 初始化用K-Means++改善质量
- 批大小设置为 b = 50 × K b = 50 \times K b=50×K
- 多次运行取最佳结果
- 结合肘部法(Elbow Method)选择K值
在工业界大规模聚类任务中,Mini-Batch K-Means已成为首选算法,在Spark MLlib、Scikit-learn等库中广泛实现。
相关文章:

【机器学习基础】机器学习入门核心算法:Mini-Batch K-Means算法
机器学习入门核心算法:Mini-Batch K-Means算法 一、算法逻辑工作流程与传统K-Means对比 二、算法原理与数学推导1. 目标函数2. Mini-Batch更新规则3. 学习率衰减机制4. 伪代码 三、模型评估1. 内部评估指标2. 收敛性判断3. 超参数调优 四、应用案例1. 图像处理 - 颜…...

机器学习实战36-基于遗传算法的水泵调度优化项目研究与代码实现
大家好,我是微学AI,今天给大家介绍一下机器学习实战36-基于遗传算法的水泵调度优化项目研究与代码实现。 文章目录 一、项目介绍二、项目背景三、数学原理与算法分析动态规划模型遗传算法设计编码方案适应度函数约束处理算法参数能量消耗模型一泵房能耗二泵房能耗效率计算模…...

计算机视觉与深度学习 | 基于Matlab的门禁指纹识别与人脸识别双系统实现
系统架构 #mermaid-svg-d8CEMhB3dNDpJu8M {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-d8CEMhB3dNDpJu8M .error-icon{fill:#552222;}#mermaid-svg-d8CEMhB3dNDpJu8M .error-text{fill:#552222;stroke:#552222;}#…...

TypeScript 定义同步方法
在TypeScript中定义同步方法是一个常见的需求,尤其是在处理不涉及异步操作的情况下。本文将详细介绍如何在TypeScript中定义和使用同步方法,包括代码示例和详细解释。 一、定义同步方法 在TypeScript中,定义同步方法与JavaScript类似&#…...

debian12.9或ubuntu,vagrant离线安装插件vagrant-libvirt,20250601
系统盘: https://mirror.lzu.edu.cn/debian-cd/12.9.0/amd64/iso-dvd/debian-12.9.0-amd64-DVD-1.iso 需要的依赖包,无需安装ruby( sudo apt install -y ruby-full ruby-dev rubygems,后来发现不安装会有编译警告,还是安装吧 ) ,无需安装 zlib1g-dev liblzma-dev libxml2-de…...

【仿muduo库实现并发服务器】使用正则表达式提取HTTP元素
使用正则表达式提取HTTP元素 1.正则表达式2.正则库的使用3.使用正则表达式提取HTTP请求行 1.正则表达式 正则表达式它其实是描述了一种字符串匹配的模式,它可以用来在一个字符串中检测一个特定格式的字串,以及可以将符合特定规则的字串进行替换或者提取…...

核心机制:流量控制
搭配滑动窗口使用的 窗口大小 窗口越大,传输速度就越快,但是也不能无限大,太大了,对于可靠性会有影响 比如发生方以非常快的速度,发送,接收方的处理速度跟不上,也就会导致有效数据被接受方丢弃(又得重传) 流量控制,就是根据接收方的处理能力(如何衡量?),干预到发送方的发送…...

Java中并发修改异常如何处理
在 Java 中,ConcurrentModificationException(并发修改异常) 是遍历集合时最常见的错误之一。它发生在迭代过程中直接修改集合结构(添加/删除元素)时,与是否多线程无关。以下是详细的处理方案: …...

极智项目 | 基于PyQT实现的YOLOv12行人目标检测软件设计
基于YOLOv12的专业级行人目标检测软件应用 开发者: 极智视界 软件下载:链接 🌟 项目特色 专业检测: 基于最新YOLOv12模型,专门针对行人检测优化现代界面: 采用PyQt5构建的美观、直观的图形用户界面高性能: 支持GPU加速,检测速…...

JavaScript 对象展开语法
文章目录 JavaScript 对象展开语法1、对象展开(Spread)操作:2、组件注册3、示例应用总结 JavaScript 对象展开语法 示例代码: export default {...student,components: {ConponentA: ConponentA,ConponentB: ConponentB},这段代…...

简单transformer运用
通俗易懂解读:hw04.py 文件内容与 Transformer 的应用 这个文件是一个 Python 脚本(hw04.py),用于完成 NTU 2021 Spring 机器学习课程的 HW4 作业任务:扬声器分类(Speaker Classification)。它…...

vscode不满足先决条件问题的解决——vscode的老版本安装与禁止更新(附安装包)
目录 起因 vscode更新设置的关闭 安装包 结语 起因 由于主包用的系统是centos的,且版本有点老了,再加上vscode现在不支持老版本的,这对主包来说更是雪上加霜啊 但是主包看了网上很多教程,眼花缭乱,好多配置要改&…...

RustDesk 搭建自建服务器并设置服务自启动
目录 0. 介绍 1. 事前准备 1.1 有公网 ip 的云服务器一台 1.2 服务端部署包 1.3 客户端安装包 2. 部署 2.1 服务器环境准备 2.2 上传服务端部署包 2.3 运行 pm2 3. 客户端使用 3.1 安装 3.2 配置 3.2.1 解锁网络设置 3.2.2 ID / 中级服务器 3.3 启动效果 > …...

【数据库】数据库恢复技术
数据库恢复技术 实现恢复的核心是使用冗余,也就是根据冗余数据重建不正确数据。 事务 事务是一个数据库操作序列,是一个不可分割的工作单位,是恢复和并发的基本单位。 在关系数据库中,一个事务是一条或多条SQL语句,…...

Qt企业级串口通信实战:高效稳定的工业级应用开发指南
目录 一、前言 二、问题代码剖析 2.1 典型缺陷示例 2.2 企业级应用必备特性对比 三、关键优化策略与代码实现 3.1 增强型串口管理类 问题1:explicit关键字的作用 3.2 智能错误恢复机制 3.3 数据分帧处理算法 四、性能优化实测数据 五、工业级应用场景 六…...

力扣HOT100之动态规划:32. 最长有效括号
这道题放在动态规划里属实是有点难为人了,感觉用动态规划来做反而更难理解了,这道题用索引栈来做相当好理解,这里先讲下索引栈的思路。 索引栈做法 我们定义一个存放整数的栈,定义一个全局变量result来记录最长有效子串的长度&a…...

深入理解前端DOM:现代Web开发的基石
什么是DOM? DOM(Document Object Model,文档对象模型)是Web开发中最重要的概念之一。它是一个跨平台、语言独立的接口,将HTML或XML文档表示为树形结构,其中每个节点都是文档的一个部分(如元素、…...

Springboot中Controller接收参数的方式
在Spring Boot中,Controller或RestController可以通过多种方式接收客户端传递的参数,主要包括以下几种常见方式: 1. 接收路径参数(PathVariable) 从URL路径中提取参数,适用于RESTful风格的API。 示例 Re…...

从一堆数字里长出一棵树:中序 + 后序构建二叉树的递归密码
从一堆数字里长出一棵树:中序 + 后序构建二叉树的递归密码 一、写在前面:一棵树的“复活计划” 作为一个老程序员,看到「中序 + 后序重建二叉树」这种题,我内心是兴奋的。为啥?它不仅是数据结构基础的“期末大题”,更是递归分解思想的典范——简洁、优雅、极具思维训练价…...
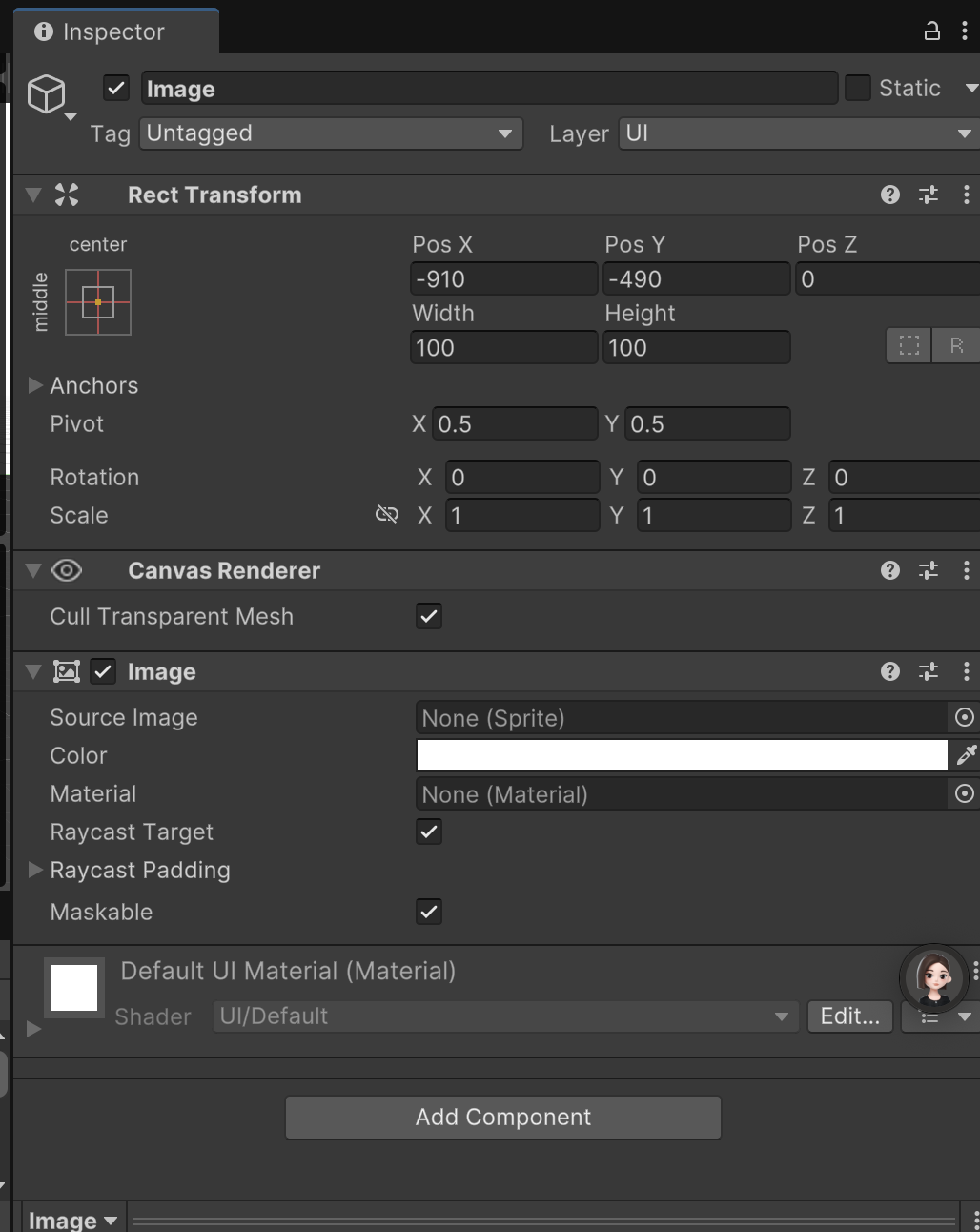
Unity UI 性能优化终极指南 — Image篇
🎯 Unity UI 性能优化终极指南 — Image篇 🧩 Image 是什么? Image 是UGUI中最常用的基本绘制组件支持显示 Sprite,可以用于背景、按钮图标、装饰等是UI性能瓶颈的头号来源之一,直接影响Draw Call和Overdraw …...

Nginx + Tomcat 负载均衡、动静分离群集
一、 nginx 简介 Nginx 是一款轻量级的高性能 Web 服务器、反向代理服务器及电子邮件(IMAP/POP3)代理服务器,在 BSD-like 协议下发行。其特点是占有内存少,并发能力强,在同类型的网页服务器中表现优异,常用…...
,安装使用完整教程】)
【maker-pdf 文档文字识别(包含ocr),安装使用完整教程】
测试效果还比较好,比markitdown要好 安装环境 conda create -n maker-pdf python3.12 conda activate marker-pdf pip install modelscope pip install marker-pdf -U下载模型 建议用modelscope上缓存的模型,不然下载会很慢 from modelscope import s…...

c++ algorithm
cheatsheet:https://hackingcpp.com transform 元素变换 https://blog.csdn.net/qq_44961737/article/details/146011174 #include <iostream> #include <vector> #include <algorithm>int main() {std::vector<int> a {1, 2, 3, 4, 5};…...
》)
《前端面试题:BFC(块级格式化上下文)》
前端BFC完全指南:布局魔法与面试必备 🎋 端午安康! 各位前端探险家,端午节快乐!🥮 愿你的代码如龙舟竞渡般乘风破浪,样式如香糯粽子般完美包裹!今天我们来解锁CSS中的布局魔法——B…...

HertzBeat的告警规则如何配置?
HertzBeat配置告警规则主要有以下步骤: 配置告警阈值 1. 登录HertzBeat管理界面,点击“阈值规则”菜单,选择“新增阈值”。 2. 选择要配置告警阈值的指标对象。例如,若监控Spring Boot应用,可选择如“状态线程数”等…...

安全-JAVA开发-第一天
目标: 安装环境 了解基础架构 了解代码执行顺序 与数据库进行连接 准备: 安装 下载IDEA并下载tomcat(后续出教程) 之后新建项目 注意点如下 1.应用程序服务器选择Web开发 2.新建Tomcat的服务器配置文件 并使用 Hello…...

6月2日上午思维训练题解
好好反思一下,自己在学什么,自己怎么在做训练赛的,真有这么难吗 ????? A - Need More Arrays 题解 想尽可能多的拆出新数组的个数,只需要从原本的数组中提取出最长的一…...

高考数学易错考点01 | 临阵磨枪
文章目录 前言集合与函数不等式数列三角函数前言 本篇内容下载于网络,网络上的都是以 WORD 版本呈现,缺字缺图很不完整,没法使用,我只是做了补充和完善。有空准备进行第二次完善,添加问题解释的链接。 集合与函数 1.进行集合的交、并、补运算时,不要忘了全集和空集的特…...
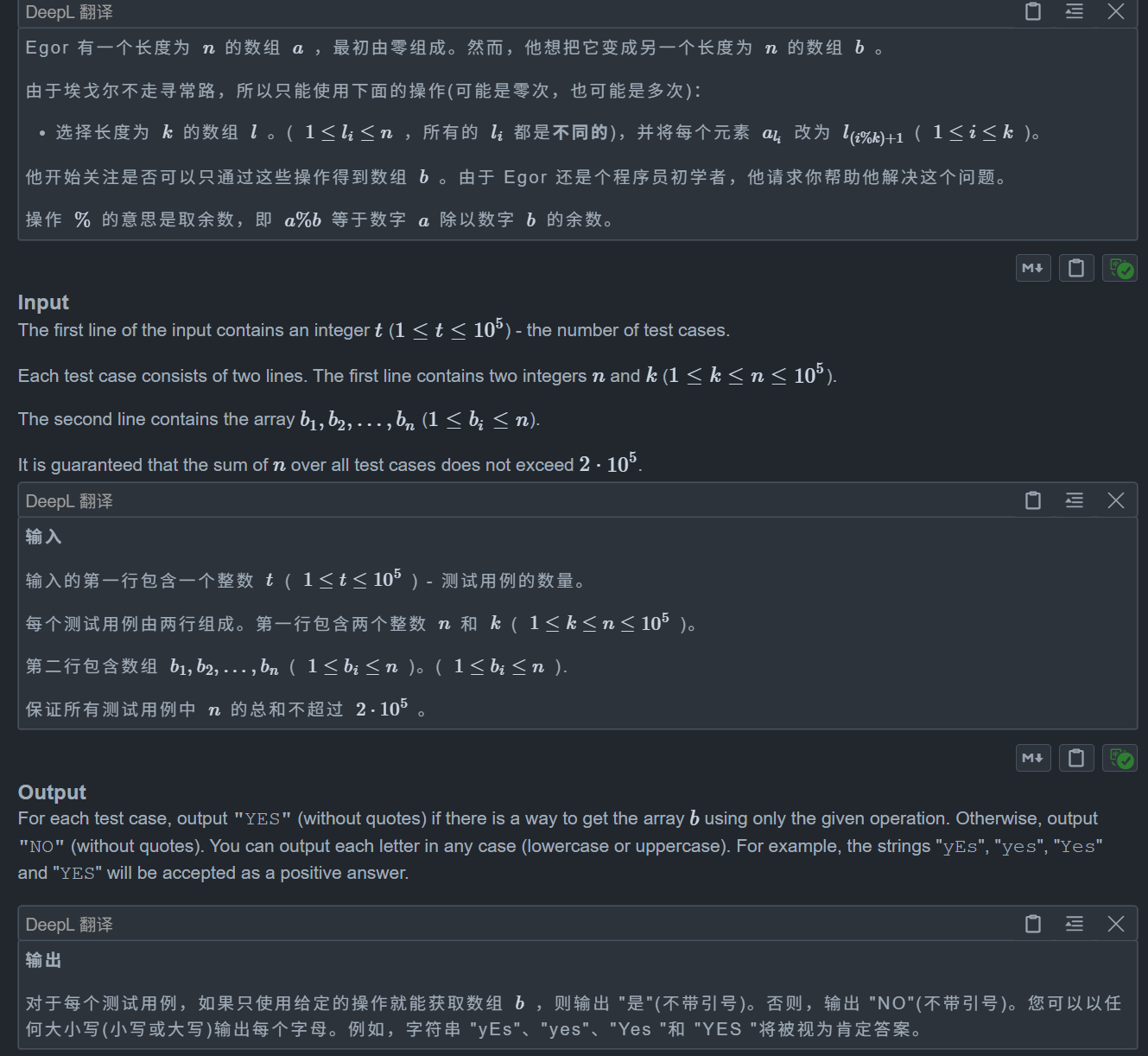
【CF】Day69——⭐Codeforces Round 897 (Div. 2) D (图论 | 思维 | DFS | 环)
D. Cyclic Operations 题目: 思路: 非常好的一题 对于这题我们要学会转换和提取条件,从特殊到一般 我们可以考虑特殊情况先,即 k n 和 k 1时,对于 k 1,我们可以显然发现必须满足 b[i] i,而…...

MySQL中的字符串分割函数
MySQL中的字符串分割函数 MySQL本身没有内置的SPLIT()函数,但可以通过其他方式实现字符串分割功能。以下是几种常见的方法: 1. SUBSTRING_INDEX函数 SUBSTRING_INDEX()是MySQL中最常用的字符串分割函数,它可以根据指定的分隔符从字符串中提…...
