力扣HOT100之动态规划:32. 最长有效括号

这道题放在动态规划里属实是有点难为人了,感觉用动态规划来做反而更难理解了,这道题用索引栈来做相当好理解,这里先讲下索引栈的思路。
索引栈做法
我们定义一个存放整数的栈,定义一个全局变量result来记录最长有效子串的长度,然后我们通过下标来遍历整个字符串s,当我们遇到(时,就将其索引压入栈中,当我们遇到)且栈顶元素对应(时,此时遇到了一对闭合的括号,我们直接将栈顶的(弹出,再用当前元素的下标i减去当前栈顶元素的下标,就能得到当前有效字串的长度,若我们遇到)但是栈顶元素不是(时,说明还没匹配上,直接将当前元素的下标压入栈中。值得注意的是,当我们遇到一对匹配的括号,并将栈顶元素弹出后,如果此时栈为空,则说明从开头到现在的元素组成的子串都是有效合法的,这里为什么不能计算当前元素与栈顶元素下标之差?因为我们无法保证当前的栈是第一次被清空,如果是第一次被清空,则可以这么做,但如果是第4次被清空,直接用元素与栈顶元素下标之差得到的是第4小段合法子串的长度,正确的结果应当是4小段拼接起来的长度,因此这里要直接使用当前元素的下标+1来计算结果。
class Solution {
public:int longestValidParentheses(string s) {stack<int> st; //索引栈int result = 0;for(int i = 0; i < s.size(); i++){if(!st.empty() && s[st.top()] == '(' && s[i] == ')'){ //遇到一对匹配的括号st.pop(); //将匹配上的'('弹出if(st.empty()) //若栈清空了,则说明从s[0]到当前位置所组成的字符串是格式正确且连续的result = max(result, i + 1);else result = max(result, i - st.top()); //若栈还没清空,则说明只是局部匹配,仅记录最外层左右括号之间的索引之差}else st.push(i);}return result;}
};
动态规划做法
感觉动态规划在状态转移的时候晦涩难懂,感觉自己想根本想不到,我是参考了一下这个大佬的题解才慢慢想明白的。建议先去看一下他的题解。接下来我们开始动规五部曲。
1.确定dp[i]的含义:以下标为i的元素结尾的情况下所能取到的最长有效子串的长度
2.确定递推公式
(1)当s[i] == '('时,dp[i] = 0;
(2)当s[i] == ')'且s[i - 1] == '('时,dp[i] = i >= 2 ? dp[i - 2] + 2 : 2;
(3)当s[i] == ')'但s[i - 1] == ‘)‘时,先判断s[i - dp[i - 1] -1]是否为’(’
如果是,当i - dp[i - 1] - 2 >= 0时,则dp[i] = dp[i - 1] + 2 + dp[i - dp[i - 1] - 2]
否则dp[i] = dp[i - 1] + 2;
3.dp数组初始化 dp[0] = 0;
4.确定遍历顺序:从左往右遍历
5.打印数组(省略)
这里重点解释下递归公式。
- 当我们以
(结尾时,无论前面的字符串是否闭合,这个字符串一定闭合不了,所以dp[i]赋值为0毫无疑问。 - 当我们以
)结尾时,如果上一个字符为(,则我们遇到了形如......()的情况,我们先判断(前是否还有字符,如果有,则dp[i] = dp[i - 2] + 2;,如果没有,则dp[i] = 2,这也很好理解。 - 当我们以
)结尾时,如果上一个字符为),则我们遇到了形如......))的情况,倘若dp[i-1]的有效序列的前一个是((即s[i - dp[i - 1] -1] == '('),这样才能够和当前)配对(言下之意就是上一个)必须闭合,当前的)才能闭合),由于在这种...((...))情况下dp[i - 1]一定会小于dp[i],我们还需要考虑与当前括号匹配的前面是否还有字符,若还有字符,则dp[i] = dp[i - 1] + 2 + dp[i - dp[i - 1] - 2];,否则dp[i] = dp[i - 1] + 2;
感觉第三种情况特别难想,好烧脑。。。
class Solution {
public:int longestValidParentheses(string s) {//1.确定dp[i]的含义:以下标为i的元素结尾的情况下所能取到的最长有效子串的长度//2.确定递推公式 //(1)当s[i] == '('时,dp[i] = 0;//(2)当s[i] == ')'且s[i - 1] == '('时,dp[i] = dp[i - 2] + 2;//(3)当s[i] == ')'但s[i - 1] == ')'时,先判断s[i - dp[i - 1] -1]是否为'('//如果是,当i - dp[i - 1] - 2 >= 0时,则dp[i] = dp[i - 1] + 2 + dp[i - dp[i - 1] - 2]//否则dp[i] = dp[i - 1] + 2;//3.dp数组初始化 dp[0] = 0;//4.确定遍历顺序:从左往右遍历//5.打印数组(省略)int result = 0;vector<int> dp(s.size(), 0);for(int i = 1; i < s.size(); i++){if(s[i] == '(') //以'('结尾一定闭合不了dp[i] = 0;else if(s[i] == ')'){if(s[i - 1] == '(') //遇到一对'(' ')',括号闭合dp[i] = i >= 2 ? dp[i - 2] + 2 : 2;else{ //遇到')'')'if(i - dp[i - 1] > 0 && s[i - dp[i - 1] -1] == '('){ //遇到"((.....))"if(i - dp[i - 1] - 2 >= 0)dp[i] = dp[i - 1] + 2 + dp[i - dp[i - 1] - 2];else dp[i] = dp[i - 1] + 2;}}}result = max(dp[i], result);}return result;}
};
相关文章:

力扣HOT100之动态规划:32. 最长有效括号
这道题放在动态规划里属实是有点难为人了,感觉用动态规划来做反而更难理解了,这道题用索引栈来做相当好理解,这里先讲下索引栈的思路。 索引栈做法 我们定义一个存放整数的栈,定义一个全局变量result来记录最长有效子串的长度&a…...

深入理解前端DOM:现代Web开发的基石
什么是DOM? DOM(Document Object Model,文档对象模型)是Web开发中最重要的概念之一。它是一个跨平台、语言独立的接口,将HTML或XML文档表示为树形结构,其中每个节点都是文档的一个部分(如元素、…...

Springboot中Controller接收参数的方式
在Spring Boot中,Controller或RestController可以通过多种方式接收客户端传递的参数,主要包括以下几种常见方式: 1. 接收路径参数(PathVariable) 从URL路径中提取参数,适用于RESTful风格的API。 示例 Re…...

从一堆数字里长出一棵树:中序 + 后序构建二叉树的递归密码
从一堆数字里长出一棵树:中序 + 后序构建二叉树的递归密码 一、写在前面:一棵树的“复活计划” 作为一个老程序员,看到「中序 + 后序重建二叉树」这种题,我内心是兴奋的。为啥?它不仅是数据结构基础的“期末大题”,更是递归分解思想的典范——简洁、优雅、极具思维训练价…...
Unity UI 性能优化终极指南 — Image篇
🎯 Unity UI 性能优化终极指南 — Image篇 🧩 Image 是什么? Image 是UGUI中最常用的基本绘制组件支持显示 Sprite,可以用于背景、按钮图标、装饰等是UI性能瓶颈的头号来源之一,直接影响Draw Call和Overdraw …...

Nginx + Tomcat 负载均衡、动静分离群集
一、 nginx 简介 Nginx 是一款轻量级的高性能 Web 服务器、反向代理服务器及电子邮件(IMAP/POP3)代理服务器,在 BSD-like 协议下发行。其特点是占有内存少,并发能力强,在同类型的网页服务器中表现优异,常用…...
,安装使用完整教程】)
【maker-pdf 文档文字识别(包含ocr),安装使用完整教程】
测试效果还比较好,比markitdown要好 安装环境 conda create -n maker-pdf python3.12 conda activate marker-pdf pip install modelscope pip install marker-pdf -U下载模型 建议用modelscope上缓存的模型,不然下载会很慢 from modelscope import s…...

c++ algorithm
cheatsheet:https://hackingcpp.com transform 元素变换 https://blog.csdn.net/qq_44961737/article/details/146011174 #include <iostream> #include <vector> #include <algorithm>int main() {std::vector<int> a {1, 2, 3, 4, 5};…...
》)
《前端面试题:BFC(块级格式化上下文)》
前端BFC完全指南:布局魔法与面试必备 🎋 端午安康! 各位前端探险家,端午节快乐!🥮 愿你的代码如龙舟竞渡般乘风破浪,样式如香糯粽子般完美包裹!今天我们来解锁CSS中的布局魔法——B…...

HertzBeat的告警规则如何配置?
HertzBeat配置告警规则主要有以下步骤: 配置告警阈值 1. 登录HertzBeat管理界面,点击“阈值规则”菜单,选择“新增阈值”。 2. 选择要配置告警阈值的指标对象。例如,若监控Spring Boot应用,可选择如“状态线程数”等…...

安全-JAVA开发-第一天
目标: 安装环境 了解基础架构 了解代码执行顺序 与数据库进行连接 准备: 安装 下载IDEA并下载tomcat(后续出教程) 之后新建项目 注意点如下 1.应用程序服务器选择Web开发 2.新建Tomcat的服务器配置文件 并使用 Hello…...

6月2日上午思维训练题解
好好反思一下,自己在学什么,自己怎么在做训练赛的,真有这么难吗 ????? A - Need More Arrays 题解 想尽可能多的拆出新数组的个数,只需要从原本的数组中提取出最长的一…...

高考数学易错考点01 | 临阵磨枪
文章目录 前言集合与函数不等式数列三角函数前言 本篇内容下载于网络,网络上的都是以 WORD 版本呈现,缺字缺图很不完整,没法使用,我只是做了补充和完善。有空准备进行第二次完善,添加问题解释的链接。 集合与函数 1.进行集合的交、并、补运算时,不要忘了全集和空集的特…...
【CF】Day69——⭐Codeforces Round 897 (Div. 2) D (图论 | 思维 | DFS | 环)
D. Cyclic Operations 题目: 思路: 非常好的一题 对于这题我们要学会转换和提取条件,从特殊到一般 我们可以考虑特殊情况先,即 k n 和 k 1时,对于 k 1,我们可以显然发现必须满足 b[i] i,而…...

MySQL中的字符串分割函数
MySQL中的字符串分割函数 MySQL本身没有内置的SPLIT()函数,但可以通过其他方式实现字符串分割功能。以下是几种常见的方法: 1. SUBSTRING_INDEX函数 SUBSTRING_INDEX()是MySQL中最常用的字符串分割函数,它可以根据指定的分隔符从字符串中提…...

前端八股之Vue
目录 有使用过vue吗?说说你对vue的理解 你对SPA单页面的理解,它的优缺点分别是什么?如何实现SPA应用呢 一、SPA 是什么 二、SPA 和 MPA 的区别 三、SPA 的优缺点 四、实现 SPA 五、给 SPA 做 SEO 的方式(基于 Vueÿ…...

Matlab数值计算
MATLAB数值计算 数值计算函数句柄匿名函数线性与非线性方程组求解1. \(左除运算)2. fzero3. fsolve4. roots 函数极值的求解1. fminbnd2. fmincon3. fminsearch与fminunc 数值积分1. quad / quadl2. quadgk3. integral4. trapz5. dblquad, quad2d, integ…...
谷歌地图高清卫星地图2026中文版下载|谷歌地图3D卫星高清版 V7.3.6.9796 最新免费版下载 - 前端工具导航
谷歌地图高清卫星地图2024中文版是一款非常专业的世界地图查看工具。通过使用该软件,你就可以在这里看到外太空星系、大洋峡谷等场景,通过高清的卫星地图,可以清晰查看地图、地形、3D建筑、卫星图像等信息,让你可以更轻松的探索世…...

条形进度条
组件 <template><view class"pk-detail-con"><i class"lightning" :style"{ left: line % }"></i><i class"acimgs" :style"{ left: line % }"></i><view class"progress&quo…...

悟饭游戏厅iOS版疑似流出:未测试版
网传悟饭游戏厅iOS版安装包流出,提供百度网盘/夸克网盘双渠道下载。本文客观呈现资源信息,包含文件验证数据、安装风险预警及iOS正版替代方案。苹果用户请谨慎测试,建议优先考虑官方渠道。 一、资源基本信息 1.1 文件验证数据 属性夸克网盘…...

95. Java 数字和字符串 - 操作字符串的其他方法
文章目录 95. Java 数字和字符串 - 操作字符串的其他方法一、分割字符串二、子序列与修剪三、在字符串中搜索字符和子字符串四、将字符和子字符串替换为字符串五、String 类的实际应用 —— 文件名处理示例示例:Filename 类示例:FilenameDemo 类 总结 95…...

IBM DB2分布式数据库架构
一、什么是分布式数据库架构 分布式数据库架构是现代数据库系统的重要发展方向,特别适合处理大规模数据、高并发访问和高可用性需求的应用场景。下面我们从原理、架构模式、关键技术、实现方式和常见产品几个方面来系统讲 1、分布式数据库的基本概念与原理 1. 什…...
)
初始化已有项目仓库,推送远程(Git)
初始化Git仓库(如果还没初始化) git init 添加并提交文件 git add . ("."表示当前项目所有文件) git commit -m “first commit” 关联远程仓库(如果还没关联) git remote add origin http://xxxxxxxx 推送代码 …...

Android Studio 向模拟器手机添加照片、视频、音乐
Android Studio 向模拟器手机添加照片、视频、音乐(其实都是一样的,只是添加到不同的文件夹),例如我们在很多程序中功能例如:选择头像,跳转到手机相册选择头像,此时相册为空,即模拟器没有图片资…...
数据结构-算法学习C++(入门)
目录 03二进制和位运算04 选择、冒泡、插入排序05 对数器06 二分搜索07 时间复杂度和空间复杂度08 算法和数据结构09 单双链表09.1单双链表及反转09.2合并链表09.2两数相加09.2分隔链表 013队列、栈、环形队列013.1队列013.2栈013.3循环队列 014栈-队列的相互转换014.1用栈实现…...

访谈 | 吴恩达全景解读 AI Agents 发展现状:多智能体、工具生态、评估体系、语音栈、Vibe Coding 及创业建议一文尽览
在最新的 LangChain Interrupt 大会上(2025),LangChain 联合创始人 & CEO Harrison Chase 与吴恩达(Andrew Ng)就 AI Agnets 的发展现状,进行了一场炉边谈话。 吴恩达回顾了与 LangChain 的渊源&#…...
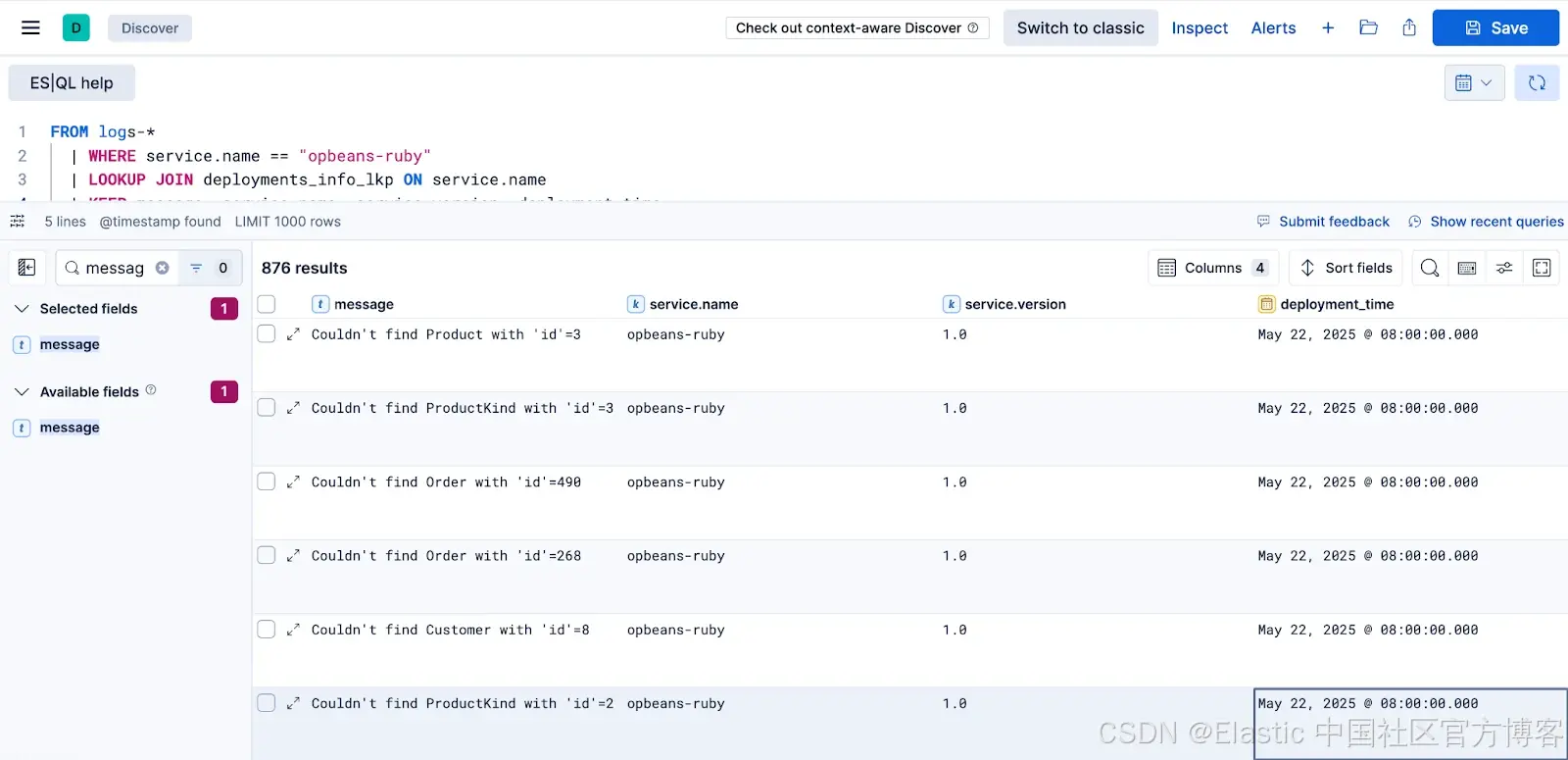
连接关键点:使用 ES|QL 联接实现更丰富的可观测性洞察
作者:来自 Elastic Luca Wintergerst ES|QL 的 LOOKUP JOIN 现已进入技术预览阶段,它允许你在查询时对日志、指标和追踪进行丰富处理,无需在摄取时进行非规范化。动态添加部署、基础设施或业务上下文,减少存储占用,加速…...

Tiktok App 登录账号、密码、验证码 XOR 加密算法
抖音 App 登录账号、密码、验证码 XOR 加密算法% E9 n z, \& R1 a4 b. ^ 流程分析 登录 Tiktok APP 时,通过抓包发现账号密码是非明文传输的。 <?php// http://xxx.xx.x.x.x/tiktok/$tiktok new TikTokClient();$userId 7212597544604484614; $secUid …...

Flask + Celery 应用
目录 Flask Celery 应用项目结构1. 创建app.py2. 创建tasks.py3. 创建celery_worker.py4. 创建templates目录和index.html运行应用测试文件 Flask Celery 应用 对于Flask与Celery结合的例子,需要创建几个文件。首先安装必要的依赖: pip install flas…...

奥威BI+AI数据分析:企业数智化转型的加速器
在当今数据驱动的时代,企业对于数据分析的需求日益增长。奥威BIAI数据分析的组合,正成为众多企业数智化转型的加速器。 奥威BI以其强大的数据处理和可视化能力著称。它能够轻松接入多种数据源,实现数据的快速整合与清洗。通过内置的ETL工具&…...
