Matlab数值计算
MATLAB数值计算
- 数值计算
- 函数句柄
- 匿名函数
- 线性与非线性方程组求解
- 1. `\`(左除运算)
- 2. `fzero`
- 3. `fsolve`
- 4. `roots`
- 函数极值的求解
- 1. `fminbnd`
- 2. `fmincon`
- 3. `fminsearch`与`fminunc`
- 数值积分
- 1. `quad` / `quadl`
- 2. `quadgk`
- 3. `integral`
- 4. `trapz`
- 5. `dblquad`, `quad2d`, `integral2`
- 6. `triplequad`, `integral3`
- 数值微分
- 1. `diff`
- 2. `polyder`
- 3. `polyval`
- 4. `spline`
- 5. `polyfit`
数值计算
函数句柄
在 MATLAB 中,当你用文件定义一个函数,比如:
function f = myfun(x)f = sin(x) - x/2;
end
这表示你创建了一个用户自定义函数 myfun,输入为 x,输出为 f。你需要将这段代码保存为文件,文件名必须是 myfun.m,并确保该文件在 MATLAB 的当前路径或工作路径下。
如何调用这个函数?
方法一:直接传值调用
myfun(1.5)ans =0.2475
方法二:使用@
x = fzero(@myfun, 1);
@myfun 是一个函数句柄,告诉 MATLAB 使用myfun函数。
匿名函数
语法:
@(x) f(x)
@后面括号中是自变量,f(x)处写函数具体形式,结果表示一个函数。若f(x)处写的是函数向量,则结果表示函数组,如fun = @(x) [x(1)^2 + x(2)^2 - 1; x(1) - x(2)]
线性与非线性方程组求解
1. \(左除运算)
用于解线性方程组 Ax = b。若矩阵 A A A可逆,则x=A \ b等价于x=inv(A)*b,若 A A A的行数大于列数且 A T A A^TA ATA可逆,则给出最小二乘解。
>> A = [2, 1; 1, 3];
>> b = [8; 13];
>> x = A \ bx =2.20003.60002. fzero
求解非线性单变量方程 f(x) = 0。
语法:
[x, fval, exitflag, output] = fzero(fun, x0, options)
输入:
fun 是目标函数,可以是:
- 字符串句柄,例如:
'sin(x)-x/2' - 函数句柄,例如:
@(x) sin(x) - x/2
x0 是初始猜测值,可以是:
- 单个数(算法从该点出发)
- 一个区间 [a, b](要求 f ( a ) f ( b ) < 0 f(a)f(b) < 0 f(a)f(b)<0,函数在区间中必须变号)
options是求解选项
输出:
x是求得的近似解fval是函数fun在x处的取值exitflag表示退出原因:- 1 1 1表示找到解
- − 1 -1 −1表示未收敛
- − 3 -3 −3表示函数在区间上不变号
output是结构体,包含迭代信息,如迭代次数、函数调用次数等
示例:
>> fun = @(x) sin(x) - x/2;
>> x0 = 1;
>> [x, fval, exitflag, output] = fzero(fun, x0)x =1.8955fval =-2.2204e-16exitflag =1output = 包含以下字段的 struct:intervaliterations: 11iterations: 6funcCount: 29algorithm: 'bisection, interpolation'message: '在区间 [0.0949033, 1.9051] 中发现零'
3. fsolve
求解非线性方程组。
语法:
[x, fval, exitflag, output, jacobian] = fsolve(fun, x0, options)
jacobian表示在解处的Jacobian矩阵
>> fun = @(x) [x(1)^2 + x(2)^2 - 1; x(1) - x(2)];
>> x0 = [0.5, 0.5];
>> [x, fval, exitflag, output, jacobian] = fsolve(fun, x0)方程已解。fsolve 已完成,因为按照函数容差的值衡量,
函数值向量接近于零,并且按照梯度的值衡量,
问题似乎为正则问题。<停止条件详细信息>x =0.7071 0.7071fval =1.0e-11 *0.22820exitflag =1output = 包含以下字段的 struct:iterations: 4funcCount: 15algorithm: 'trust-region-dogleg'firstorderopt: 3.2275e-12message: '方程已解。...'jacobian =1.4142 1.41421.0000 -1.00004. roots
求解一元多项式的所有根。
语法:
roots(c)
c是多项式的系数向量,按降幂排序
>> c = [1 -3 2]; % 表示 x^2 - 3x + 2
>> r = roots(c)r =21>>
函数极值的求解
MATLAB只求最小值
1. fminbnd
求解有界有约束单变量函数的最小值,约束体现在是求解区间上的最小值。
语法:
[x, fval, exitflag, output]=fminbnd(fun, x1, x2, options)
给出fun在 [ x 1 , x 2 ] [x_1, x_2] [x1,x2]上的最小值点与最小值。
示例:
>> f = @(x) (x-2).^2;
>> [x, fval, exitflag, output] = fminbnd(f, 0, 4)x =2fval =0exitflag =1output = 包含以下字段的 struct:iterations: 5funcCount: 6algorithm: 'golden section search, parabolic interpolation'message: '优化已终止:...'2. fmincon
求解有约束多变量函数的最小值。
语法:
[x,fval] = fmincon(fun, x0, A, b, Aeq, beq, lb, ub, nonlcon, options)
fun目标函数x0初始点(必须给)A, b线性不等式约束 A x ⩽ b Ax\leqslant b Ax⩽bAeq, beq线性等式约束 A e q x = b e q Aeq x = beq Aeqx=beqlb, ub变量下界和上界nonlcon非线性约束函数,返回[c(x), ceq(x)]options优化参数
如果某些约束没有,可用 [] 占位
示例:
最小化目标函数:
f ( x 1 , x 2 ) = ( x 1 − 2 ) 2 + ( x 2 − 1 ) 2 s.t. { x 1 + x 2 ⩽ 3 x 1 − x 2 = 0 x 1 2 + x 2 2 − 4 ⩽ 0 sin ( x 1 + x 2 ) − 1 = 0 0 ⩽ x 1 ⩽ 2 , 0 ⩽ x 2 ⩽ 2 \begin{gather*} f(x_1,x_2)=(x_1-2)^2+(x_2-1)^2 \\ \operatorname{s.t.} \begin{cases} x_1+x_2\leqslant3 \\ x_1-x_2=0 \\ x_1^2+x_2^2-4\leqslant0 \\ \sin(x_1+x_2)-1=0 \\ 0\leqslant x_1\leqslant2,\quad0\leqslant x_2\leqslant2 \end{cases} \end{gather*} f(x1,x2)=(x1−2)2+(x2−1)2s.t.⎩ ⎨ ⎧x1+x2⩽3x1−x2=0x12+x22−4⩽0sin(x1+x2)−1=00⩽x1⩽2,0⩽x2⩽2
% 非线性约束函数文件nonlcon.m
function [c, ceq] = nonlcon(x)% 非线性不等式:c(x) <= 0c = x(1)^2 + x(2)^2 - 4;% 非线性等式:ceq(x) = 0ceq = sin(x(1) + x(2)) - 1;
end% 目标函数
>> fun = @(x) (x(1) - 2)^2 + (x(2) - 1)^2;% 初始点
>> x0 = [1; 1];% 线性不等式约束 A*x <= b
>> A = [1, 1];
>> b = 3;% 线性等式约束 Aeq*x = beq
>> Aeq = [1, -1];
>> beq = 0;% 变量上下界
>> lb = [0; 0];
>> ub = [2; 2];% 求解
>> [x_opt, fval, exitflag, output] = fmincon(fun, x0, A, b, Aeq, beq, lb, ub, @nonlcon)找到具有较低目标函数值的可行点,但不满足最优性条件。请参阅 output.bestfeasible。可能存在局部最小值。满足约束。fmincon 已停止,因为当前步长小于
步长容差值并且在约束容差值范围内满足约束。<停止条件详细信息>x_opt =0.78540.7854fval =1.5213exitflag =2output = 包含以下字段的 struct:iterations: 27funcCount: 93constrviolation: 2.2204e-16stepsize: 8.0922e-11algorithm: 'interior-point'firstorderopt: 0.0814cgiterations: 0message: '可能存在局部最小值。满足约束。...'bestfeasible: [1x1 struct]3. fminsearch与fminunc
二者是求无约束多变量最小值问题的函数,其中fminsearch使用Nelder-Mead法。
[x,fval,exitflag,output] = fminsearch(fun, x0, options)
[x,fval,exitflag,output] = fminunc(fun, x0, options)
>> fun = @(x) (x(1) - 3)^2 + (x(2) + 1)^2 + sin(x(1));
>> x0 = [0, 0];
>> [x, fval, exitflag, output] = fminsearch(fun, x0)x =3.4728 -1.0000fval =-0.1016exitflag =1output = 包含以下字段的 struct:iterations: 78funcCount: 148algorithm: 'Nelder-Mead simplex direct search'message: '优化已终止:...'>> [x, fval, exitflag, output] = fminunc(fun, x0)找到局部最小值。优化已完成,因为梯度大小小于
最优性容差的值。<停止条件详细信息>x =3.4728 -1.0000fval =-0.1016exitflag =1output = 包含以下字段的 struct:iterations: 7funcCount: 24stepsize: 6.9597e-05lssteplength: 1firstorderopt: 2.3117e-07algorithm: 'quasi-newton'message: '找到局部最小值。...'
数值积分
1. quad / quadl
自适应辛普森法与自适应 Lobatto 高阶法求积分
语法:
[q, n] = quad(fun, a, b, tol)
[q, n] = quadl(fun, a, b)
q返回积分值,n返回函数计算的次数,tol表示精度,默认为 10 − 6 10^{-6} 10−6,上式表示计算函数fun从a到b的积分
示例:
>> f = @(x) x.^2;
>> quad(f, 0, 1)ans =0.3333>> quadl(f, 0, 1)ans =0.33332. quadgk
高精度 Gauss-Lobatto 法
语法
[q, err] = quadgk(fun, a, b)
err表示误差估计
示例:
>> f = @(x) sin(x)./x;
>> [q, err] = quadgk(f, 0.1, 10)q =1.5584err =1.7052e-163. integral
全局自适应辛普森公式
语法:
q = integral(fun, a, b)
示例:
>> f = @(x) exp(-x.^2);
>> I = integral(f, -Inf, Inf)I =1.77254. trapz
梯形公式
语法:
I = trapz(x, y)
示例:
>> x = 0:0.1:10;
>> y = sin(x);
>> I = trapz(x, y)I =1.83755. dblquad, quad2d, integral2
计算二重积分。
语法:
q = dblquad(fun, xmin, xmax, ymin, ymax, tol, method)
q = quad2d(fun, xmin, xmax, ymin, ymax)
q = integral2(fun, xmin, xmax, ymin, ymax)
示例:
>> f = @(x, y) x .* y;
>> q = dblquad(f, 0, 1, 0, 1)q =0.2500>> q = quad2d(f, 0, 1, 0, 1) q =0.2500>> q = integral2(f, 0, 1, 0, 1)q =0.25006. triplequad, integral3
三重积分。
语法:
q = triplequad(fun, xmin, xmax, ymin, ymax, zmin, zmax)
q = integral3(fun, xmin, xmax, ymin, ymax, zmin, zmax)
示例:
>> f = @(x, y, z) x + y + z;
>> q = integral3(f, 0, 1, 0, 1, 0, 1)q =1.5000>> q = triplequad(f, 0, 1, 0, 1, 0, 1)q =1.5000数值微分
1. diff
向前差分。
语法:
% 计算向量 x 的一阶向前差分:x(i+1) - x(i)
diff(x, n)
% 对矩阵 A 的第 dim 个维度计算 n 阶向前差分,dim = 1(默认):按列方向差分,dim = 2:按行方向差分
diff(A, n, dim)
示例:
>> x = [1 2 4 7];
>> dx = diff(x)dx =1 2 3>> dx = diff(x, 2)dx =1 1>> A = [1 2; 4 5; 9 10];
>> dA = diff(A, 1, 1)dA =3 35 5>> dA = diff(A, 1, 2)dA =1112. polyder
求多项式导函数。
语法:
dp = polyder(p) % 求多项式 p 的导函数
dp = polyder(p, q) % 求 p*q 的导函数
[dp, dq] = polyder(p, q) % 求 p/q 的导函数,dp返回分子多项式的系数,dq返回分母多项式的系数
示例:
>> p = [3 0 -4]; % 表示 3x^2 - 4
>> dp = polyder(p) % 导数为 6x dp =6 0>> p = [1 2]; % p(x) = x + 2
>> q = [3 0 -1]; % q(x) = 3x^2 - 1
>> dpq = polyder(p, q) % 求 (p*q)的导函数dpq =9 12 -1>> p = [1 2]; % 分子 p(x) = x + 2
>> q = [1 -1]; % 分母 q(x) = x - 1
>> [num, den] = polyder(p, q)num =-3den =1 -2 13. polyval
多项式求值。
p = [1 -3 2];
y = polyval(p, 2)y =04. spline
三次样条插值。
语法:
yi = spline(x, y, xi)
x, y是已知数据点xi是需要插值的位置- 返回
yi = f(xi)
示例:
>> x = 0:10;
>> y = sin(x);
>> xi = 0:0.1:1;
>> yi = spline(x, y, xi)yi =0 0.1118 0.2181 0.3187 0.4134 0.5017 0.5837 0.6588 0.7270 0.7880 0.84155. polyfit
数据拟合为多项式。
语法:
[p, S, mu] = polyfit(x, y, n)
拟合n次多项式,返回误差结构体,mu中第一个元素为x的均值,第二个元素为x的标准差
示例:
>> x = 1:5;
>> y = [2.2 2.8 3.6 4.5 5.1];
>> [p, S, mu] = polyfit(x, y, 1)p =1.1859 3.6400S = 包含以下字段的 struct:R: [2x2 double]df: 3normr: 0.1643rsquared: 0.9952mu =3.00001.5811相关文章:

Matlab数值计算
MATLAB数值计算 数值计算函数句柄匿名函数线性与非线性方程组求解1. \(左除运算)2. fzero3. fsolve4. roots 函数极值的求解1. fminbnd2. fmincon3. fminsearch与fminunc 数值积分1. quad / quadl2. quadgk3. integral4. trapz5. dblquad, quad2d, integ…...
谷歌地图高清卫星地图2026中文版下载|谷歌地图3D卫星高清版 V7.3.6.9796 最新免费版下载 - 前端工具导航
谷歌地图高清卫星地图2024中文版是一款非常专业的世界地图查看工具。通过使用该软件,你就可以在这里看到外太空星系、大洋峡谷等场景,通过高清的卫星地图,可以清晰查看地图、地形、3D建筑、卫星图像等信息,让你可以更轻松的探索世…...

条形进度条
组件 <template><view class"pk-detail-con"><i class"lightning" :style"{ left: line % }"></i><i class"acimgs" :style"{ left: line % }"></i><view class"progress&quo…...

悟饭游戏厅iOS版疑似流出:未测试版
网传悟饭游戏厅iOS版安装包流出,提供百度网盘/夸克网盘双渠道下载。本文客观呈现资源信息,包含文件验证数据、安装风险预警及iOS正版替代方案。苹果用户请谨慎测试,建议优先考虑官方渠道。 一、资源基本信息 1.1 文件验证数据 属性夸克网盘…...

95. Java 数字和字符串 - 操作字符串的其他方法
文章目录 95. Java 数字和字符串 - 操作字符串的其他方法一、分割字符串二、子序列与修剪三、在字符串中搜索字符和子字符串四、将字符和子字符串替换为字符串五、String 类的实际应用 —— 文件名处理示例示例:Filename 类示例:FilenameDemo 类 总结 95…...

IBM DB2分布式数据库架构
一、什么是分布式数据库架构 分布式数据库架构是现代数据库系统的重要发展方向,特别适合处理大规模数据、高并发访问和高可用性需求的应用场景。下面我们从原理、架构模式、关键技术、实现方式和常见产品几个方面来系统讲 1、分布式数据库的基本概念与原理 1. 什…...
)
初始化已有项目仓库,推送远程(Git)
初始化Git仓库(如果还没初始化) git init 添加并提交文件 git add . ("."表示当前项目所有文件) git commit -m “first commit” 关联远程仓库(如果还没关联) git remote add origin http://xxxxxxxx 推送代码 …...

Android Studio 向模拟器手机添加照片、视频、音乐
Android Studio 向模拟器手机添加照片、视频、音乐(其实都是一样的,只是添加到不同的文件夹),例如我们在很多程序中功能例如:选择头像,跳转到手机相册选择头像,此时相册为空,即模拟器没有图片资…...
数据结构-算法学习C++(入门)
目录 03二进制和位运算04 选择、冒泡、插入排序05 对数器06 二分搜索07 时间复杂度和空间复杂度08 算法和数据结构09 单双链表09.1单双链表及反转09.2合并链表09.2两数相加09.2分隔链表 013队列、栈、环形队列013.1队列013.2栈013.3循环队列 014栈-队列的相互转换014.1用栈实现…...

访谈 | 吴恩达全景解读 AI Agents 发展现状:多智能体、工具生态、评估体系、语音栈、Vibe Coding 及创业建议一文尽览
在最新的 LangChain Interrupt 大会上(2025),LangChain 联合创始人 & CEO Harrison Chase 与吴恩达(Andrew Ng)就 AI Agnets 的发展现状,进行了一场炉边谈话。 吴恩达回顾了与 LangChain 的渊源&#…...
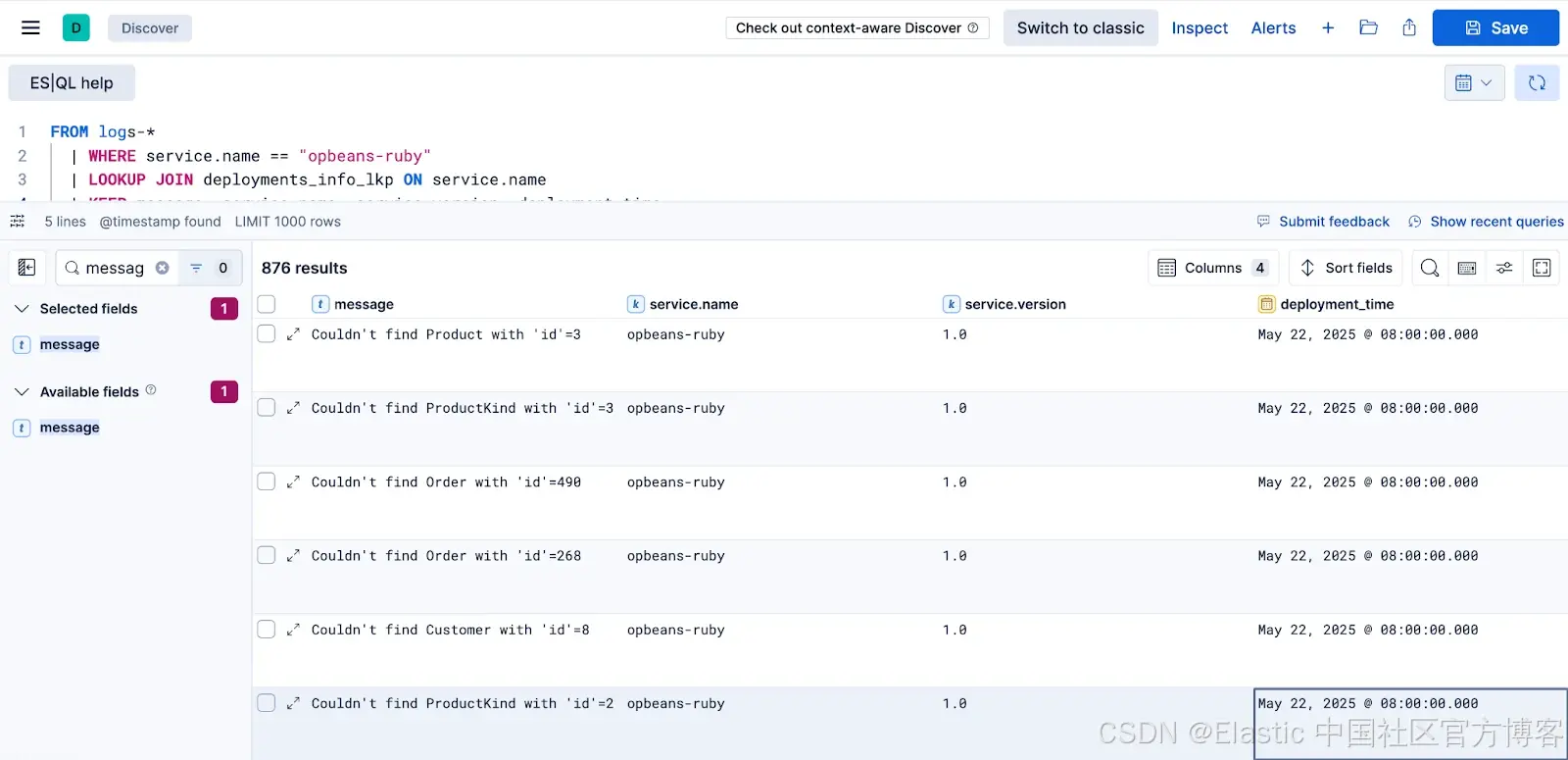
连接关键点:使用 ES|QL 联接实现更丰富的可观测性洞察
作者:来自 Elastic Luca Wintergerst ES|QL 的 LOOKUP JOIN 现已进入技术预览阶段,它允许你在查询时对日志、指标和追踪进行丰富处理,无需在摄取时进行非规范化。动态添加部署、基础设施或业务上下文,减少存储占用,加速…...

Tiktok App 登录账号、密码、验证码 XOR 加密算法
抖音 App 登录账号、密码、验证码 XOR 加密算法% E9 n z, \& R1 a4 b. ^ 流程分析 登录 Tiktok APP 时,通过抓包发现账号密码是非明文传输的。 <?php// http://xxx.xx.x.x.x/tiktok/$tiktok new TikTokClient();$userId 7212597544604484614; $secUid …...

Flask + Celery 应用
目录 Flask Celery 应用项目结构1. 创建app.py2. 创建tasks.py3. 创建celery_worker.py4. 创建templates目录和index.html运行应用测试文件 Flask Celery 应用 对于Flask与Celery结合的例子,需要创建几个文件。首先安装必要的依赖: pip install flas…...

奥威BI+AI数据分析:企业数智化转型的加速器
在当今数据驱动的时代,企业对于数据分析的需求日益增长。奥威BIAI数据分析的组合,正成为众多企业数智化转型的加速器。 奥威BI以其强大的数据处理和可视化能力著称。它能够轻松接入多种数据源,实现数据的快速整合与清洗。通过内置的ETL工具&…...

python打卡day43
复习日 作业: kaggle找到一个图像数据集,用cnn网络进行训练并且用grad-cam做可视化 进阶:并拆分成多个文件 找了个街头食物图像分类的数据集Popular Street Foods(其实写代码的时候就开始后悔了),原因在于&…...

MySQL 如何判断某个表中是否存在某个字段
在MySQL中,判断某个表中是否存在某个字段,可以通过查询系统数据库 INFORMATION_SCHEMA.COLUMNS 实现。以下是详细步骤和示例: 方法:使用 INFORMATION_SCHEMA.COLUMNS 通过查询系统元数据表 COLUMNS,检查目标字段是否存…...

Linux --进程优先级
概念 什么是进程优先级,为什么需要进程优先级,怎么做到进程优先级这是本文需要解释清楚的。 优先级的本质其实就是排队,为了去争夺有限的资源,比如cpu的调度。cpu资源分配的先后性就是指进程的优先级。优先级高的进程有优先执行的…...

安装和配置 Nginx 和 Mysql —— 一步一步配置 Ubuntu Server 的 NodeJS 服务器详细实录6
前言 昨天更新了四篇博客,我们顺利的 安装了 ubuntu server 服务器,并且配置好了 ssh 免密登录服务器,安装好了 服务器常用软件安装, 配置好了 zsh 和 vim 以及 通过 NVM 安装好Nodejs,还有PNPM包管理工具 。 作为服务器的运行…...

Linux 测试本机与192.168.1.130 主机161/udp端口连通性
Linux 测试本机与 192.168.1.130 主机 161/UDP 端口连通性 161/UDP 端口是 SNMP(简单网络管理协议)的标准端口。以下是多种测试方法: 🛠️ 1. 使用 nmap 进行专业测试(推荐) sudo nmap -sU -p 161 -Pn 1…...

OpenCV 滑动条调整图像亮度
一、知识点 1、int createTrackbar(const String & trackbarname, const String & winname, int * value, int count, TrackbarCallback onChange 0, void * userdata 0); (1)、创建一个滑动条并将其附在指定窗口上。 (2)、参数说明: trackbarname: 创建的…...

图解gpt之注意力机制原理与应用
大家有没有注意到,当序列变长时,比如翻译一篇长文章,或者处理一个长句子,RNN这种编码器就有点力不从心了。它把整个序列信息压缩到一个固定大小的向量里,信息丢失严重,而且很难记住前面的细节,特…...

硬件学习笔记--65 MCU的RAM及FLash简介
MCU(微控制器单元)内部的 RAM 和 Flash 是最关键的两种存储器,它们直接影响MCU的性能、功耗和编程方式。以下是它们的详细讲解及作用: 1. RAM(随机存取存储器) 1.1 特性 1)易失性:…...

【Oracle】视图
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 视图基础概述1.1 视图的概念与特点1.2 视图的工作原理1.3 视图的分类 2. 简单视图2.1 创建简单视图2.1.1 基本简单视图2.1.2 带计算列的简单视图 2.2 简单视图的DML操作2.2.1 通过视图进行INSERT操作2.2.2 通…...
 与 MySQL (SQL) 的写法对比)
数据库 MongoDB (NoSQL) 与 MySQL (SQL) 的写法对比
MongoDB (NoSQL) 与 MySQL (SQL) 的写法对比及优劣势分析 基本概念差异 MySQL/SQL:关系型数据库,使用结构化查询语言(SQL),数据以表格形式存储,有预定义的模式(schema)MongoDB/NoSQL:文档型数据库,无固定…...

基于粒子滤波的PSK信号解调实现
基于粒子滤波的PSK信号解调实现 一、引言 相移键控(PSK)是数字通信中广泛应用的调制技术。在非高斯噪声和动态相位偏移环境下,传统锁相环(PLL)性能受限。粒子滤波(Particle Filter)作为一种序列蒙特卡洛方法,能有效处理非线性/非高斯系统的状态估计问题。本文将详细阐…...

更强劲,更高效:智源研究院开源轻量级超长视频理解模型Video-XL-2
长视频理解是多模态大模型关键能力之一。尽管OpenAI GPT-4o、Google Gemini等私有模型已在该领域取得显著进展,当前的开源模型在效果、计算开销和运行效率等方面仍存在明显短板。近日,智源研究院联合上海交通大学等机构,正式发布新一代超长视…...

2025.6.3学习日记 Nginx 基本概念 配置 指令 文件
1.初始nginx Nginx(发音为 “engine x”)是一款高性能的开源 Web 服务器软件,同时也具备反向代理、负载均衡、邮件代理等功能。它由俄罗斯工程师 Igor Sysoev 开发,最初用于解决高并发场景下的性能问题,因其轻量级、高…...

【连接器专题】案例:产品测试顺序表解读与应用
在查看SD卡座连接器的规格书,一些测试报告时,你可能会看到如下一张产品测试顺序表。为什么会出现一张测试顺序表呢? 测试顺序表的使用其实定义测试环节的验证的“路线图”和“游戏规则”,本文就以我人个经验带领大家一起看懂这张表并理解其设计逻辑。 测试顺序表结构 测试…...

星动纪元的机器人大模型 VPP,泛化能力效果如何?与 VLA 技术的区别是什么?
点击上方关注 “终端研发部” 设为“星标”,和你一起掌握更多数据库知识 VPP 利用了大量互联网视频数据进行训练,直接学习人类动作,减轻了对于高质量机器人真机数据的依赖,且可在不同人形机器人本体之间自如切换,这有望…...

4000万日订单背后,饿了么再掀即时零售的“效率革命”
当即时零售转向价值深耕,赢面就是综合实力的强弱。 文|郭梦仪 编|王一粟 在硝烟弥漫的外卖行业“三国杀”中,饿了么与淘宝闪购的日订单量竟然突破了4000万单。 而距淘宝闪购正式上线,还不到一个月。 在大额福利优惠…...
